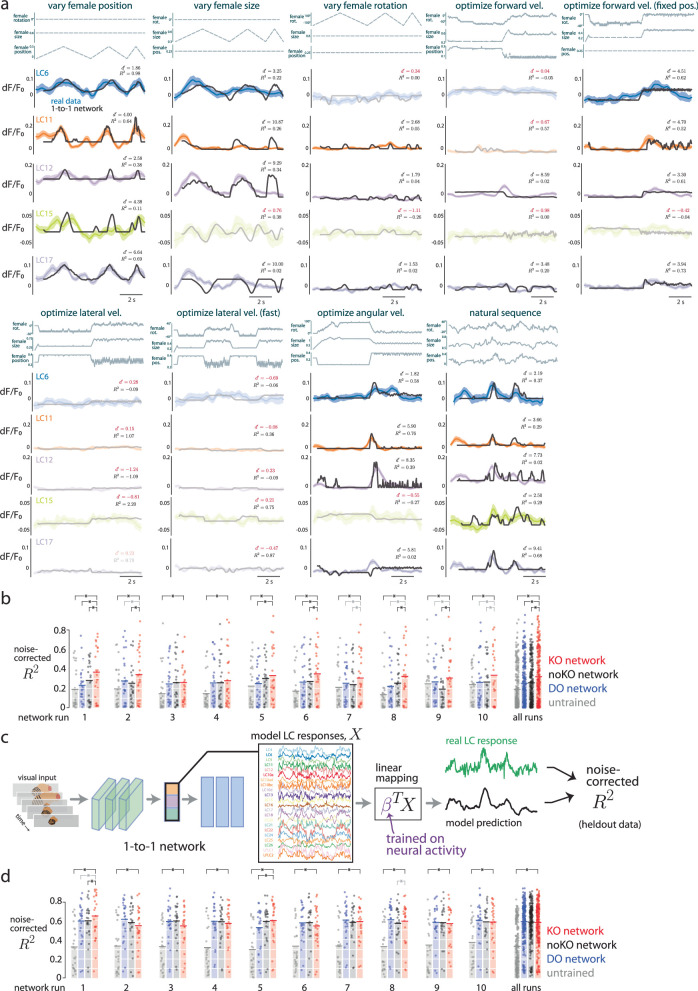
Extended Data Fig. 8. Real LC responses and predicted responses to stimulus sequences of a moving fictive female.

a. We considered 9 different stimulus sequences in which a female varied her rotation, size, and position (three top traces for each stimulus sequence, see Methods for stimulus descriptions). We found that the 1-to-1 network’s predictions (black traces) largely predicted the responses of the real LC neurons (color traces), despite the facts that the 1-to-1 network was never given access to neural data and that we directly read out from a single model LC unit. The average of all reported noise-corrected R²s here is the same as that reported in Fig. 2e. We only considered stimulus sequences for which the real LC responses reliably varied across time for the stimulus sequence. To measure this, we computed the $d^{\prime }$ between splits of repeats (i.e., a signal-to-noise ratio across repeats) and considered any stimulus sequence with a $d^{\prime }<1$ as unreliable, removing it from our analyses (translucent traces; see Methods). For some LC types, we detected a reliable response to only one or a few stimuli (e.g., LC15 only responded to ‘vary female position’ and ‘natural sequence’). We noticed that none of the LC neurons responded to stimulus sequences for which the fictive female’s parameters were chosen to optimize the 1-to-1 network’s output of lateral velocity (‘optimize lateral vel.’ and ‘optimize lateral vel. (fast)’, see Methods). This may be due to the fast changes in female position which were not present in other stimulus sequences. For each stimulus and LC type, we computed a noise-corrected R² between the real and model predicted responses. This noise-corrected R² overlooks any differences in mean, standard deviation, and sign of the response, which are unidentifiable by the KO network. For visual clarity, we centered, scaled, and flipped the sign of the 1-to-1 network predictions (black traces) to match the mean, standard deviation, and sign of the LC responses (color traces) for each stimulus. We accounted for the smoothness of calcium traces by applying a causal smoothing filter to the model LC responses as well as fitting the mean offset of the relu thresholding (see Methods). Interestingly, all LC types responded reliably to varying female position (‘vary female position’, color traces) despite the facts that the optic glomeruli have weak retinotopy^12,61 and that the calcium trace is a sum of the activity of almost all neurons for the same LC type (presumably averaging away any spatial information). This suggests that either our targeted region for calcium imaging (Fig. 2a) was biased to read out from a subset of LC neurons with nearby receptive fields or that these LC neurons have some selectivity in female position (perhaps as direction selectivity). The latter may be more likely, as the male needs to better estimate female position than can be done simply by comparing coarse differences between the two optic lobes. Consistent with our findings, a previous study has identified another LC type—LC10a—to respond to an object’s position¹¹. That our 1-to-1 network also predicted positional selectivity in the LC types (black traces) supports the notion that some optic glomeruli may track female position despite weak retinotopy. More work is needed to understand how object position is encoded within a single optic glomerulus and how that information is read out⁶¹. b. Results in a were for a KO network with one random initialization. To see if this effect holds for different initializations, we trained 10 runs of the KO network, each with a different random initialization and random ordering of training samples. We compared the runs of the KO network to those of the dropout (DO) network, for which a randomly-chosen model LC unit was dropped out during training, as well as noKO networks for which no knockout occurred during training. These are the same networks used to predict moment-to-moment behavior (Extended Data Fig. 3d). Each bar denotes the mean R², and each dot denotes one combination of LC type and stimulus (i.e., non-shaded traces in a). Black asterisks denote a significant increase in mean R² (p < 0.05, paired, one-sided permutation test, n = 27), gray asterisks denote a trend (p < 0.15). We observed that random initialization played more of a role for neural prediction than for behavioral prediction (Extended Data Fig. 3d). This is not so surprising, as the networks were never trained to predict neural responses. Still, the KO networks tended to outperform the other types of networks (red bars larger than other bars); combining across all runs, the KO network performed significantly better (‘all runs’, p < 0.002 for comparisons between KO and other networks, paired, one-sided permutation test, n = 270). In addition, the untrained networks performed poorly (gray bars), indicating that training networks on behavior did improve neural predictions. c. For the results in a and b, we considered a one-to-one mapping in which we directly compared a model LC unit’s response with real LC responses; our 1-to-1 network never had access to neural data for training. Here, we wondered if we relaxed this assumption (i.e., train a linear mapping from all model LC units to real LC responses), to what extent would the model’s prediction of real LC responses improve. The basic setup was the following. We feed a stimulus sequence into the 1-to-1 network (fully trained with knockout training) and collect responses from all model LC units, denoted as $X\in {\mathcal{R}}^{K\times T}$ for K model LC units (here, K = 23) and the T timepoints of the stimulus sequence. We then define a linear mapping $\beta \in {\mathcal{R}}^K$ to map the K model LC responses to the real LC response. We use real LC responses to train β. Specifically, for each of the 4 cross-validation folds, we train β on 75% of the real LC responses (randomly selected) using ridge regression. Training the linear mapping on responses to other stimuli led to worse performance, as expected, because the stimuli were largely different from each other—training on responses to a fictive female changing in position was not predictive of responses to a fictive female changing in size. We then predict the responses for the remaining held-out timepoints. We concatenate the predictions across the 4 folds and then compute the noise-corrected R² in the same way as in Fig. 2d,e. Thus, the reported cross-validated noise-corrected R²s indicate the extent to which the 1-to-1 network, given neural data on which to train, can predict held-out real LC responses. Another view is that in this setting, the 1-to-1 network is a task-driven model trained on behavioral data with an internal representation (the model LC bottleneck) that reflects the activity of real LC neurons up to a linear transformation¹. d. Prediction performance using the linear mapping for different networks and network runs (see Methods). For each network, we trained a new linear mapping between the model LC responses and the real LC responses. Overall, prediction performance greatly increased: The 1-to-1 network (or KO network) with the linear mapping had a noise-corrected R² at ~ 65% (network run 1, averaged over all recorded LCs and fictive female stimulus sequences), an additive increase of ~ 30% over that of the 1-to-1 network with the one-to-one mapping comparison ( ~ 35%, Fig. 2e). We also found that, for the linear mapping, the performance of the 1-to-1 network was similar to those of the other networks trained with dropout (DO) or no knockout (noKO) (leftmost plot, red bar close to black and blue bars). This similarity in performance was not unexpected and indicates that all 3 networks (KO, DO, and noKO) have similar internal representations (up to a linear transformation) at the layer of their LC bottlenecks. However, the 1-to-1 network’s representation is better aligned to the LC types along its coordinate axes—where each model LC unit corresponds to one axis—than those of the other networks (Fig. 2e). Networks trained with behavioral data (KO, DO, and noKO) outperformed an untrained network (gray bar), indicating that training on behavior was helpful in identifying LC response properties. That the untrained network was somewhat predictive of LC responses (bar for ‘untrained’ above 0) stems from an inductive bias in which the network’s convolutional filters, even with randomized weights, can detect large changes of the visual stimulus (e.g., a fictive female moving back and forth). That a linear combination of random features is often predictive in a regression setting is a well-studied phenomenon in machine learning⁶² and has been observed in predicting visual cortical responses⁶³. This trend in similarity of performance held across all 10 network runs (same runs as in b) for the different training procedures: The KO network consistently better predicted real LC responses than the untrained network but less so when compared to the DO and noKO networks (red bars at similar heights to black and blue bars across network runs). This trend held when combining across all runs (‘all runs’). A black asterisk indicates a KO network with a mean prediction performance significantly above that of another network (p < 0.05, paired, one-sided permutation test); a gray asterisk indicates a trend (0.05 < p < 0.15). Each bar denotes the mean R², and each dot denotes one LC type and stimulus combination (i.e., the non-shaded traces in a); n = 27 for statistical tests for each run and n = 270 for all runs. Network run 1 was the chosen 1-to-1 network for Figs. 1–4. The results here indicate that by simply training a network on courtship behavioral data (i.e., a task-driven approach), we have identified a highly-predictive image-computable model of LC neurons. To our knowledge, ours is the first image-computable model of the LC population proposed. An important point is that this encoding model (using a linear mapping) does not identify a one-to-one mapping between model LC units and LC types, as the model is unable to relate the encoded LC neurons to behavior—this is precisely the reason we built the 1-to-1 network. Training the 1-to-1 network both on behavior and neural responses is a worthwhile goal, but care is needed to ensure the neural responses are recorded during natural behavior to achieve as best a match as possible.

Source data