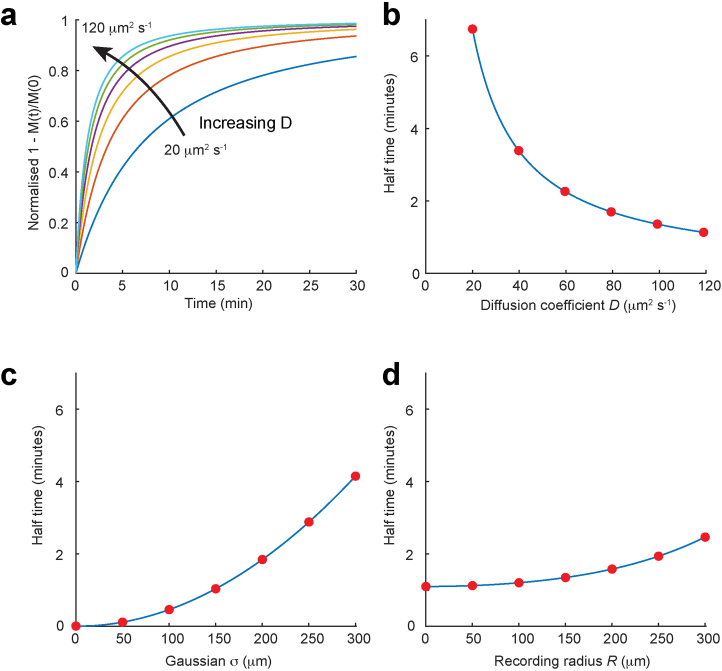
Extended Data Fig. 2. The time course of M(t) (equation [5]) is sensitive to values of D and σ, but insensitive to values of R.

a, The time course of M(t)/M(0) for values of D from 20–120 μm² s⁻¹. b, Corresponding half times of M(t)/M(0) over the same range of D showing that the half times change greatly with D. c, Corresponding half times of M(t)/M(0) over the same range of D showing that the half times change greatly with σ. d, Corresponding half times of M(t)/M(0) over the same range of D showing that the half times change little with R. Derivation of equation [5]. The total number of mols M(t) of fluorescent dye in a hemisphere of radius R, is given by equation [2] multiplied by the area of a hemisphere (2πr²), integrated from 0→R (because we have assumed that the volume being recorded from is a hemisphere of radius R): $M\left(t\right)=C\left(0,0\right){\left[1+\frac{2Dt}{{\sigma }^2}\right]}^{-\frac{3}{2}}\underset{0}{\overset{R}{\int }}2\pi r^{2}exp\left[\frac{-r^2}{4Dt+2{\sigma }^2}\right]dr$ This can be written as: $M\left(t\right)=a\underset{0}{\overset{R}{\int }}{r}^{2}exp\left[-b{r}^2\right]dr$, where $a=2\pi C\left(0,0\right){\left[1+\frac{2Dt}{{\sigma }^2}\right]}^{-\frac{3}{2}}$ and $b={\left(4Dt+2{\sigma }^2\right)}^{-1}$ Integrating by parts gives: $M\left(t\right)=\left[-\frac{aR}{2b}exp\left[-b{R}^2\right]\right]+\underset{0}{\overset{R}{\int }}\frac{a}{2b}exp\left[-b{r}^2\right]dr$ Using the standard integral: $\underset{0}{\overset{R}{\int }}exp\left[-b{r}^2\right]dr=\sqrt{\frac{\pi }{4b}}erf\left(\sqrt{b}R\right)$, we have $M\left(t\right)=\frac{a}{2b}\left\{\sqrt{\frac{\pi }{4b}}erf\left(\sqrt{b}R\right)-Rexp\left[-b{R}^2\right]\right\}$ so, finally, substituting in a and b we have Equation [5]: $M\left(t\right)=\frac{2\pi C\left(0,0\right){\sigma }^3}{\sqrt{\left(2Dt+{\sigma }^2\right)}}\left\{\sqrt{\frac{\pi \left(2Dt+{\sigma }^2\right)}{2}}erf\left(\frac{R}{\sqrt{\left(4Dt+2{\sigma }^2\right)}}\right)-Rexp\left[-\frac{R^2}{\left(4Dt+2{\sigma }^2\right)}\right]\right\}$.