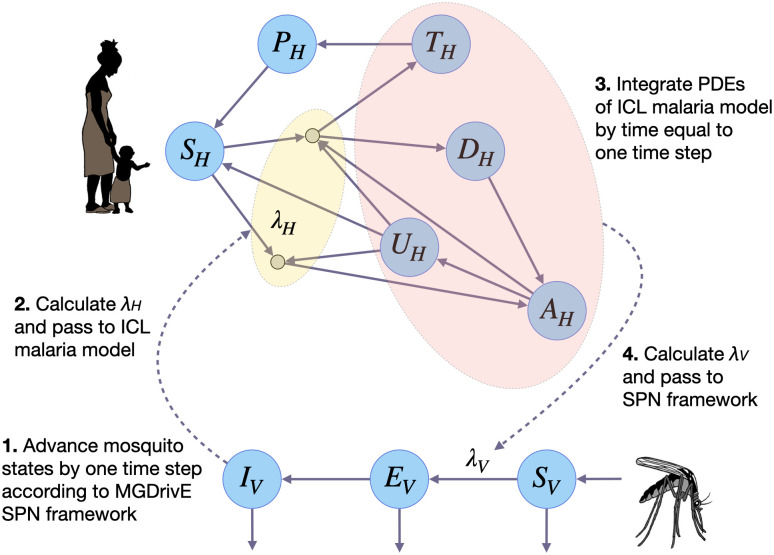
Fig 1. Schematic of decoupled vector-host sampling algorithm for malaria.
MGDrivE 3 uses a stochastic Petri net framework to model progression of adult female mosquitoes from susceptible (SV) to exposed/latently infected (EV) to infectious for malaria (IV). This framework is linked to an adapted version of the Imperial College London (ICL) malaria model, which is represented as a set of partial differential equations. In the ICL model, humans progress from susceptible (SH) to either symptomatic or asymptomatic infection. Humans who develop a symptomatic infection and are either treated (TH) or diseased and untreated (DH). Treated humans advance to a prophylactic protection state (PH) and eventually become susceptible again. Untreated symptomatic humans develop successively lower-density infections, from symptomatic to asymptomatic but detectable by rapid diagnostic test (RDT) (AH) to asymptomatic and undetectable by RDT (UH). Asymptomatic humans can also be super-infected. To allow the two frameworks to communicate, at each time step: i) the ICL human model samples the force of infection in humans (λH) from the MGDrivE 3 vector model, ii) the ICL human model increments its infectious states for a time equal to one time step, iii) the MGDrivE 3 vector model samples the force of infection in vectors (λV) from the ICL human model, and iv) the MGDrivE 3 vector model increments its infectious states for one time step.