Quantifying image quality in AOSLO images of photoreceptors

Abstract

The use of “quality” to describe the usefulness of an image is ubiquitous but is often subject to domain specific constraints. Despite its continued use as an imaging modality, adaptive optics scanning light ophthalmoscopy (AOSLO) lacks a dedicated metric for quantifying the quality of an image of photoreceptors. Here, we present an approach to evaluating image quality that extracts an estimate of the signal to noise ratio. We evaluated its performance in 528 images of photoreceptors from two AOSLOs, two modalities, and healthy or diseased retinas. The algorithm was compared to expert graders’ ratings of the images and previously published image quality metrics. We found no significant difference in the SNR and grades across all conditions. The SNR and the grades of the images were moderately correlated. Overall, this algorithm provides an objective measure of image quality that closely relates to expert assessments of quality in both confocal and split-detector AOSLO images of photoreceptors.

1. Introduction

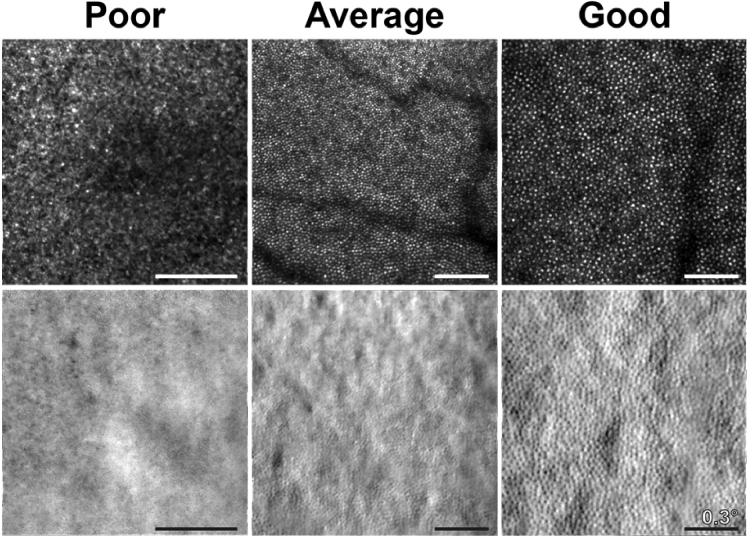
The term ‘image quality’ is deceptively simple, and typically refers to the appearance of an image as subjectively determined by a viewer. For this reason, often what constitutes “good” image quality is inferred from myriad of factors including operational knowledge gained from time spent using an imaging device, institutional, or guideline-based knowledge, and practical knowledge gained from processing and analyzing the resultant images. Indeed, what individuals call “poor” or “good” image quality can wildly vary (Fig. 1) and may vary substantially from person to person. To avoid a purely subjective assessment of image quality, many clinical-grade imaging devices such as OCTs provide some form of on-device objective estimate of image quality, aiding operators and providing a benchmark for successful image acquisition. These objective measurements of image quality are essential for the consistent evaluation, grouping, and comparison of data between imaging devices. Moreover, objective measurements of image quality are essential for establishing exclusion criterion for images obtained as a part of clinical trials [1,2]. Surprisingly, there are relatively few reports of image quality metrics in adaptive optics (AO) ophthalmoscopy [3,4], with most used as metrics for sensorless AO [4–8].

Fig. 1.

Qualitative examples of AOSLO confocal and split-detector images of the human retina deemed to be of subjectively poor, average, and good quality.

Besides producing a noisy, distorted, or a minimally useful image, the presence of poor image quality in AOSLOs can cause significant and costly logistical challenges, including significantly increased imaging time, costly follow-up imaging, or a failed imaging session. Even for ostensibly high-quality datasets, location-specific focus, detector gains, and wavefront correction differences mean that multiple videos from the same location often have varying quality.

For nearly all ophthalmoscopes, the earliest evaluation of image quality occurs at acquisition time. In particular, the quality of AOSLO images can degrade due to multiple factors such as poor AO correction, poor ocular media, eye motion, tear film degradation, and more [9]. Most often, imaging technicians make real-time image quality judgements based on numerous factors, including mean intensity, AO correction metrics (RMS, Strehl ratio), or subjective assessments of image noise, contrast, and feature visibility.

Once collected, image quality is evaluated again during post-processing. Often the initial burden of assessing image quality erroneously falls to registration metrics such as normalized cross correlation [10–13], mutual information [14], and root mean square error [15]. However, these metrics are necessarily robust to noise and are designed for image alignment to a reference image, not as descriptors of image quality. While there exist algorithms capable of rejecting poor reference images before alignment based on metrics such as mean intensity, contrast, and sharpness [16,17], the quality of the final registered image is not always related to the quality of the reference image, and ultimately a user is still required to select suitable quality images from a subset of registered and averaged candidate images.

Metrics designed explicitly for assessing image quality broadly fall into two categories: reference and no-reference. Reference-based image quality metrics are calculated relative to some reference image or value that describes a high- or low-quality baseline. One recently published tool for AOSLO images enables an automated ranking of registered or montaged images from best to worst [18]. Others include metrics such as the structural similarity index metric (or SSIM) [3], and the image sharpness ratio [19]. These types of metrics are valuable for measuring image quality improvement or deterioration, but as referenced algorithms they are ultimately limited to relational judgements, and are not designed to provide an absolute, quantitative estimate of image quality.

For this reason, no-reference image quality metrics are often more desirable for evaluating AOSLO images. This includes metrics like mean intensity [8,5], contrast [6], sharpness [16,17], Fourier coefficient energy [6,7], Blind Image Quality Index (BIQI) [3,20,21], and Perception-based Image Quality Evaluator (PIQE) [21]. Many of these have found extensive use in sensorless AO, where they are used as metrics to drive optimization of an AO control loop but are not commonly reported in literature as a descriptive measure. While they perform well in an optimization context, their values are not necessarily representative of the quality of an image. For example, mean intensity can vary with the number of features separate from image quality (e.g. tear film, detector gain), and contrast and sharpness vary based on the features present in the image. BIQI and PIQE evaluate quality assuming the presence of distortions from image compression artifacts such as JPEG, white noise and Gaussian blur, however AOSLO images of photoreceptors often violate these assumptions as they are uncompressed, averaged, and consist of numerous Gaussian-shaped objects.

Thus, it is of interest to develop and validate a no-reference, quantitative image quality metric (IQM) suitable for evaluating AOSLO images of photoreceptors. Objective measurement of an AOSLO image’s quality would not only improve data acquisition efficiency, but significantly reduce logistical waste. In addition, objective measurements of image quality will remove the need for subjective and reference-based assessment of images. In this work we designed and validated an IQM to provide accurate, no-reference image quality measurements of AOSLO images.

2. Methods

2.1. Human subjects:

The images acquired for our dataset were retrospectively obtained from two AOSLOs at Marquette University (MU) and the Medical College of Wisconsin (MCW). Subjects gave informed consent prior to the images being collected. The Institutional Review Board of MCW and Children’s Wisconsin approved the studies in which these images were obtained (PRO00038673, PRO00017439, CHW 07/77), and the datasets themselves were collected in accordance with the tenets of the Declaration of Helsinki. Retinal images in the dataset were chosen at random from individuals both with (n = 12) and without pathology (n = 26). Images of pathological retina came from six subjects with retinitis pigmentosa, four subjects with cone-rod dystrophy, and two subjects with Stargardt disease. All subjects were dilated prior to imaging with one drop each of tropicamide (1%) and phenylephrine (2.5%).

2.2. Image collection:

The retrospective dataset consisted of randomly selected images from AOSLOs of comparable design. One AOSLO was housed at MU (Boston Micromachines Corporation (BMC); Cambridge, Massachusetts) and the other at MCW [22]. For imaging illumination, the MU device uses an 850 ± 60 nm super-luminescent diode with a power at the eye of 197µW over a 7.5 mm pupil (SLD; Superlum, Killacloyne Ireland), the MCW device uses a 775 ± 13 nm SLD (Inphenix, Livermore, California) with a power at the eye of 167.7µW over an 8 mm pupil. Imaging framerates were either 15.7 or 29.9 Hz in the MU device, and 16.6 Hz in the MCW device.

A total of 528 images were used, half from each institution (264), and half again from the AOSLO’s confocal and split-detector modalities (132 each) [23] which were obtained simultaneously. Images were obtained 0-10 degrees (mean eccentricity = 4.1°) from the subject’s preferred retinal locus using fields of view (FOV) ranging from 0.75 to 1.75 degrees. The data was balanced between the two institutions through matching the number of images at each retinal location and is available in Dataset 1 ^{(122.1MB, zip)} [24].

Images used from each device were processed according to the standard practices at MU and MCW. Videos collected at MU were first registered using custom software from BMC using a strip-registration approach. Following registration, images were dewarped to remove residual distortion [25]. Videos collected at MCW were desinusoided to remove static distortions using a Ronchi ruling, registered using a previously described strip-registration approach [11], then dewarped using the same approach as at MU.

2.3. Automatically quantifying image quality in AO-ophthalmoscopy images of photoreceptors:

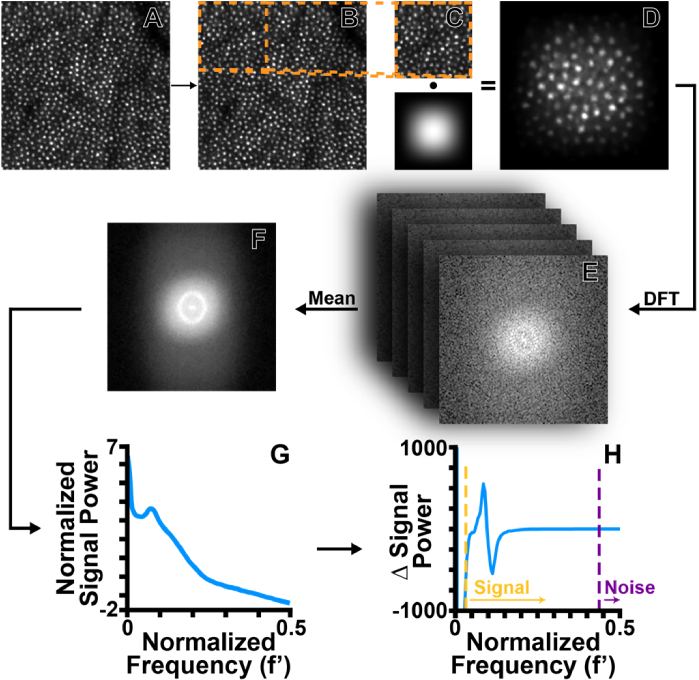
Our objective measure of an image’s signal to noise ratio (SNR) is based on an analysis of differentiated Fourier coefficients. First, we obtained a reduced noise estimate of the Discrete Fourier Transform (DFT) via Welch’s method [26]. This method is described briefly as follows: a series of regions of interest (ROIs) that were 25% of the total image size while overlapping by 50% (Fig. 2(A)-(C)) were extracted. Each ROI was then multiplied with a matched-size Hanning window [26,27] and Discrete Fourier Transformed (Fig. 2(D)). Finally, all DFTs were averaged to obtain a low noise (and reduced resolution) power spectrum of the initial image (Fig. 2(E)).

Fig. 2.

Flowchart of the algorithm used to automatically assess image quality. From each image selected for analysis (A), an ROI is extracted following Welch’s method (B). After extraction, we multiply the ROI with a matched dimension Hanning window (C) and perform a DFT on the windowed ROI (D). All ROI DFTs are averaged to obtain a single, high quality, and reduced resolution DFT of the entire image (E). The high quality DFT is transformed to polar coordinates and then averaged across all angles (F). Finally, power as a function of increasing frequency is differentiated (G). Empirically determined normalized thresholds corresponding to putative ‘signal’ and ‘noise’ values were used (H). Finally, the absolute value of the signal and noise ranges integrated and divided by one another. This value was converted to decibels for the final SNR value.

Next, the power spectrum was converted to polar coordinates using a pseudo-polar transform [28]. All angles of the pseudo-polar power spectrum were then averaged (Fig. 2(F)). We then differentiated the average pseudo-polar power spectrum to de-emphasize low frequencies (Fig. 2 G). We chose normalized low and high cutoff frequency values based on the sizes of feasibly visible cells (e.g. cones and rods) in AOSLO images (low: ∼2 arcmins, or ∼0.03 normalized frequency; high: ∼0.27 arcmins, or 0.35 normalized frequency). The “signal” in our SNR calculation was thus defined as the values located between the high and low frequency cutoff values, and “noise” was defined as all values not within the high and low frequency range, while excluding exceptionally low frequencies along with the DC term (Fig. 2 H). Following this, the absolute value of the differentiated signal and noise ranges were integrated to determine their arclength. Finally, SNR was calculated from the ratio of the signal to noise in decibels, where dP_S is the differentiated power of the signal vector, dP_n is the differentiated power of the noise vector, df′ is the differentiated normalized frequency vector, and n is the length of each vector (Eq. (1)):

$$SNR=10lo{g}_{10}\left(\frac{\frac{1}{n}\sum \left|\frac{d{P}_s}{d{f}^{\mathrm{\prime }}}\right|}{\frac{1}{n}\sum \left|\frac{d{P}_n}{d{f}^{\mathrm{\prime }}}\right|}\right)$$ (1)

2.4. Expert assessment of image quality:

For comparison with the automated algorithm, three experienced graders (Grader 1: 25 years, Grader 2: 5 years, Grader 3: 14 years) were recruited to grade the AOSLO images using cell visibility as the primary benchmark of quality. Grading was facilitated with a custom MATLAB script that randomly presented each image, masking users to any identifying information. All images were contrast adjusted over the 1^st and 99^th percentile of intensity values, but not resized to a common FOV. The graders were prompted to enter a grade between 0 and 5 for each image, where a grade of zero was very poor quality and five was of the highest quality. Each grader was provided with a standard grading criterion (Table 1) alongside instructions on how to operate the software to grade each image. Results from each grader were saved to a text file and returned for analysis.

Table 1. Instructions provided to experienced graders for classifying the images of the dataset.

GRADE	DESCRIPTION
0	Cannot distinguish any cones/rods throughout the entire image
1	The cones/rods are only countable in only a small section/portion of the image and the rest of the image is not countable
2	The cones/rods are easily countable in certain areas of the image but on average the image is not easily countable
3	The cones/rods are easily countable in over half of the image and mostly countable in the other half of the image
4	The cones/rods for the most part are easily identifiable and countable for the entire image
5	The cones/rods can be easily identified and counted throughout the entire image

Grading agreement was assessed using a weighted Kappa. To assess the association between image grades and SNR values, Pearson correlation coefficients were obtained and compared first for each modality then between devices using a non-parametric permutation test.

2.5. Analysis of individual AOSLO video frames

A natural extension of the IQM algorithm is to evaluate its performance on individual frames of AOSLO videos for real-time feedback during an imaging session, or as guidance for post-processing. To assess the effect of intraframe distortions from eye motion on SNR, we extracted a subset of 1,120 frames from 10 randomly selected raw videos in the MU confocal dataset. We manually sorted these frames into two groups, those that had significant intraframe motion and those that did not and assessed the degree of overlap.

We also evaluated the algorithm’s ability to estimate final image quality from individual video frames. To do this, we first computed individual frame SNR, then calculated the mean SNR of all frames from a video. The difference between the registered image’s SNR and the average SNR from all frames was then compared to the number of frames that were averaged during the registration process.

2.6. Comparison to existing no-reference metrics of image quality

Finally, we compared our algorithm’s performance to existing measures of image quality. There are numerous general purpose image quality metrics, so we selected three that were designed to capture a range of features, ranging from simple to complex: mean intensity, contrast, and PIQE. PIQE is an image quality metric based on human perception where lower values indicate a higher quality [21]. Contrast was calculated using a previously described approach based on row- and column-wise coefficients of variance [6], and we used MATLAB’s native implementation of PIQE (see MATLAB’s piqe function).

2.7. Statistical analysis

Due to the relatively large sample size of the dataset and absence of highly influential outliers, SNR and grade outcomes were summarized by sample means and standard deviations and analyzed with Hotelling and t-tests. Histograms were used to visualize distributions of SNR and grade measures separately for different devices and across different graders. Since split-detector and confocal modalities acquired from the same video were highly correlated, devices were compared with Hotelling trace. If the Hotelling trace test is significant, a post-hoc two-sample t-test is performed for comparing each modality between the devices. We performed a similar comparison between images from pathologic and non-pathologic retinas.

Agreements between pairs of graders were described with Bland-Altman plots and jittered (noise added) to visualize individual observations with the same values. This association analysis between SNR and grades for split-detector and confocal modalities was completed separately for each device. The statistical significance of Pearson’s correlation was determined with a permutation test.

3. Results

3.1. SNR across modalities and devices

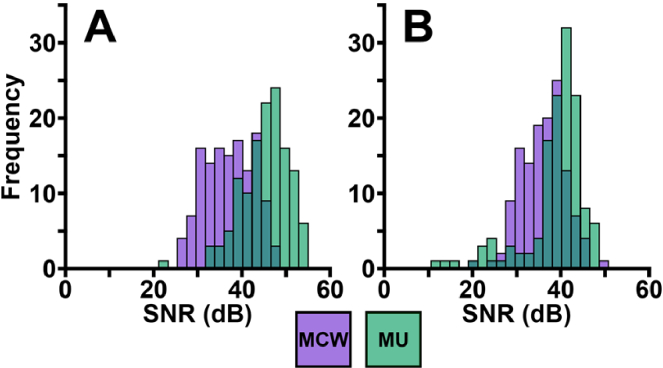
We obtained SNR measurements and grades (three per image­ from each grader) for all 528 images (Dataset 1 ^{(122.1MB, zip)} , [24]). The distribution of SNR values across both institutions and modalities had considerable overlap (Fig. 3). For MU images, the average (±standard deviation) SNR was 45.1 ± 5.3 dB for confocal images and 38.6 ± 6.8 dB for split-detector images. For MCW images, the average SNR was 37.2 ± 5.5 dB for confocal images and 36.1 ± 5.0 dB for split-detector images (Table 2). Due to the split and confocal images being from the same video they are thus correlated. First, a Pearson correlation was calculated to quantify the strength of association between SNR modalities separately for each device. We found that SNR of simultaneously obtained confocal and split-detector images were moderately correlated for both MCW (r = 0.67; p < 0.001) and MU (r = 0.47; p < 0.001) AOSLOs. As these correlations were highly statistically significant, we applied a Hotelling’s trace test to determine if the two-dimensional SNR mean (confocal and split-detector modalities) were different between the two devices. As it was significant (p < 0.001), we then compared SNR modalities between MU and MCW devices using two post-hoc two-sample t-tests (one for confocal and one for split-detector). The difference between the means across devices was found to be significantly different for both modalities (p < 0.001).

Fig. 3.

Calculated SNR values for both confocal (A) and split-detector (B) AOSLO images from both imaging devices (MCW = purple, MU = green).

Table 2. Average and standard deviation of the proposed algorithm and other image quality metrics. Higher SNR and contrast values denote better image quality, whereas lower PIQE scores denote better image quality.

	MU		MCW
	Confocal	Split-Detector	Confocal	Split-Detector
IQM (dB)	45.12 ± 5.27	38.61 ± 6.78	37.16 ± 5.43	36.1 ± 4.96
Mean Intensity	64.04 ± 19.9	125.94 ± 5.36	39.45 ± 9.47	125.55 ± 11.11
PIQE	55.23 ± 18.0	65.46 ± 24.21	36.5 ± 13.96	25.54 ± 11.37
Contrast	0.35 ± 0.1	0.05 ± 0.03	0.62 ± 0.1	0.21 ± 0.03

3.2. Grader analysis

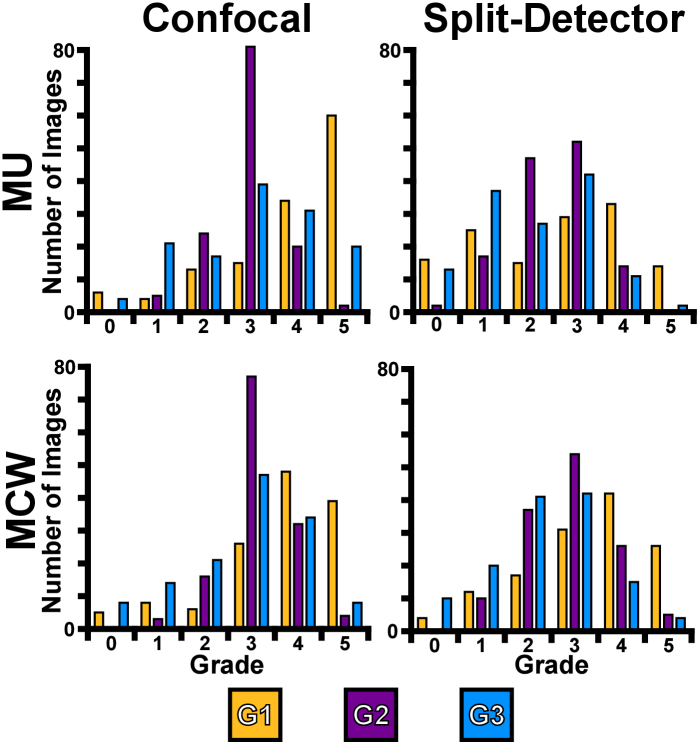
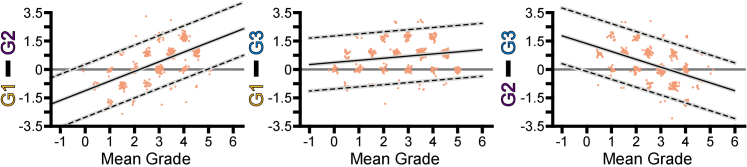
Qualitatively, grader ratings had similar distributions across modalities and devices (Fig. 4). The average grade for MU data was 3.3 ± 1.3 and 2.4 ± 1.3 for confocal and split-detector images, respectively, and the average grades for MCW were 3.2 ± 1.2 and 2.8 ± 1.2 for confocal and split-detector images. To assess agreement between graders, we generated three pairs of Bland-Altman plots (Fig. 5). Systematic mean differences (SMD) increased as a function of mean grade in Graders 1 and 2 (slope = 0.59; intercept = -1.3) and 1 and 3 (slope = 0.13; intercept = 0.42). It decreased as a function of mean grade between Graders 2 and 3 (slope = -0.45; intercept = 1.6) (Fig. 5). The weighted Kappa indicated a poor to fair but significant relationship (p < 0.001) between Graders 1 and 2 (0.35), 1 and 3 (0.46), and 2 and 3 (0.38).

Fig. 4.

Visual representation of the individual grades for all images across devices (MU and MCW) and modalities (confocal and split-detector) for all graders (G1 = Grader 1, G2 = Grader 2, G3 = Grader 3).

Fig. 5.

Bland Altman plots depicting the difference between each pair of graders for all images with jitter added for visualization only (left: Grader 1 vs Grader 2; center: Grader 1 vs Grader 3; right: Grader 2 vs Grader 3). Limits of agreement are shown as dashed black lines while SMD is depicted by the solid black line. The 95% confidence intervals are shown as gray boxes.

3.3. Interactions between SNR and grade

The relationship between average grades, modalities, and devices was analyzed using the approach described above. First, the Pearson’s correlation was determined between modalities of the average grades for each device. The average grade for confocal and split-detector modalities were weakly (r = 0.18) but significantly (p = 0.035) correlated for the MCW AOSLO while the average grade for the MU AOSLO were moderately (r = 0.47) and significantly (p < 0.001) correlated. Following this, a Hotelling’s trace test was performed and determined to be significant (p < 0.001). As the trace test was significant, we used a post-hoc two-sample t-test to compare modalities across the MU and MCW devices and found that confocal was not significantly different between devices (p = 0.34) but split-detector average grades were significantly different (p < 0.001).

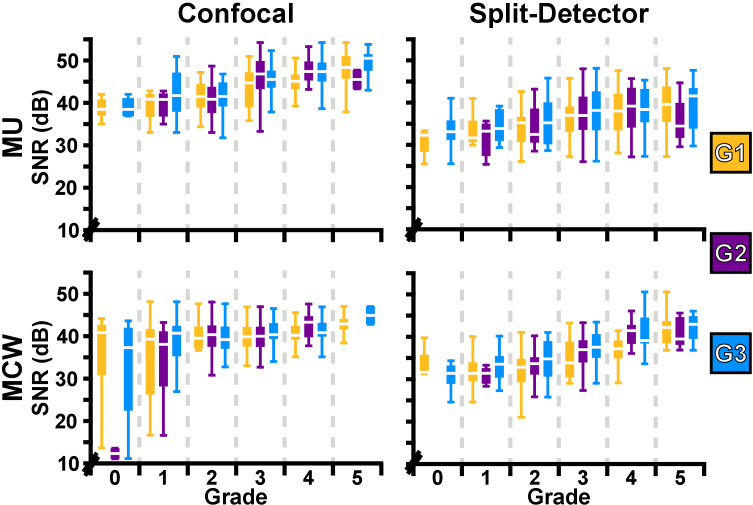
We observed that SNR increased monotonically as a function of grade regardless of modality or device (Fig. 6). To compare the SNR to the graders’ scores, a Pearson correlation was performed between the SNR and the average grade for each modality. The average grade and SNR exhibited a moderate, but significant correlation for the confocal modality (r = 0.39; p < 0.001); the split-detector modality exhibited similar behavior (r = 0.44; p < 0.001). We performed a permutation test to compare the correlation coefficients between devices and found a significant difference (p < 0.001).

Fig. 6.

Boxplots for visualization of the relationship between SNR and grade across modalities (confocal and split-detector) and AOSLOs (MU and MCW) for each of the graders.

3.4. SNR and grade in pathology

To assess the algorithm’s performance in different image populations, we compared SNR between images of pathological and non-pathological retinas. For images of pathological retina, average SNR and grade was 38.9 ± 5.8 dB and 2.2 ± 1.1 for confocal images, respectively, and 38.3 ± 5.5 dB and 2.0 ± 1.0 for split-detector images. For images of non-pathological retina, average SNR and grade was 42.0 ± 6.8 dB and 3.6 ± 0.69 for confocal images, respectively, and 37.0 ± 6.3 dB and 2.8 ± 1.1 for split-detector images. As above, a Hotelling’s trace test was used to compare pathological and non-pathological images across modalities for both SNR and grade. There was a significant difference between SNR and grade of images of pathological and non-pathological retina (p < 0.001). Post hoc two-sample t-tests indicated significant differences between confocal SNR, confocal grade, and split-detector grade (p < 0.001). However, there was not a significant difference in split-detector SNR (p = 0.12).

3.5. SNR applied to individual video frames

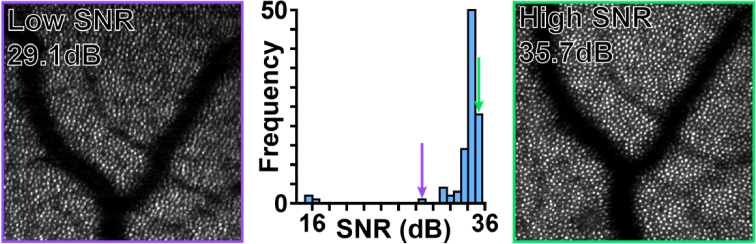
Individual frames exhibited a wide range of SNRs with ‘low’ SNR frames often corresponding to defocus (Fig. 7, purple box), blinks, or substantial intraframe motion (Supplemental Figure 1), and ‘high’ SNR corresponding to frames usable for registration (Fig. 7, green box).

Fig. 7.

Histogram of SNR values from each frame in a single confocal video, center, with frames from this video representing a visualization of a high SNR, right, and a low SNR, left. The images visualizing the different SNR values are marked in the histogram with the corresponding color.

When we assessed the effect of intraframe motion on individual frame SNR, we found that 55 frames out of 1,120 contained clear intraframe motion (4.9%). There was considerable overlap between the SNR of frames with and without intraframe motion (Supplemental Figure 2). In most cases, distorted images consisted of largely good or excellent image quality with a single distortion present in the frame.

We observed a strong correlation between the final averaged image and the mean of the individual frame SNR (Spearman r = 0.75; p < 0.001; Fig. 8), culminating in a roughly $\sqrt{n}$ -fold relationship expected when averaging multiple well-correlated images [29].

Fig. 8.

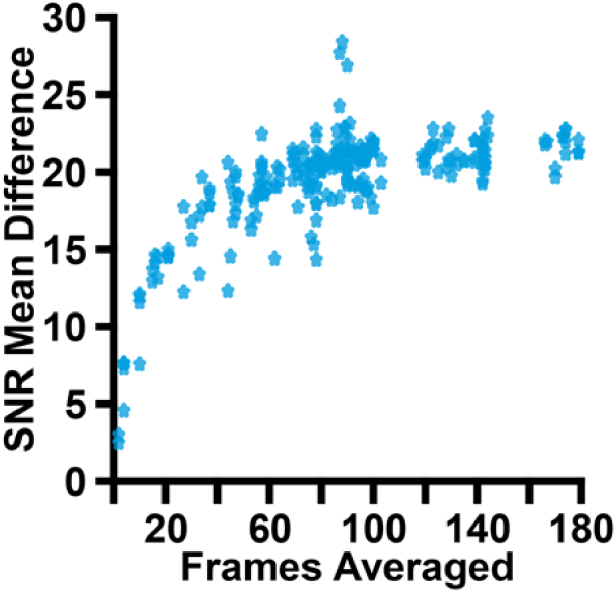
Comparison of the difference between the registered image’s SNR and the mean SNR of all frames from the MU videos and the number of frames averaged in the video. The trend visualized is the expected $\sqrt{n}$ curve when averaging is performed.

3.6. SNR compared to existing measures of image quality

We found substantially different relationships between mean image intensity, contrast, and PIQE and the average grade than between SNR and average grade (Table 2). First, mean intensity was substantially different between MU and MCW for confocal images, but not split-detector images, likely due to the “centering” (adding half the dynamic range to the subtracted direct and reflect channels) performed by the split-detector algorithms [30]. Contrast (see Supplemental Figure 4) and PIQE (see Supplemental Figure 5) also varied as a function of device and modality and had consistently higher values for the MU device (55-65), than the MCW device (25-36; Table 2).

Mirroring the analysis used to assess the relationship between SNR and graders’ scores, Pearson correlations were performed between the other metrics and the average grade. As we observed that these metrics varied substantially as a function of both modality and device (Table 2), we performed Pearson correlations between each metric and average grade across each modality and device.

Mean image intensity and average grade were not significantly correlated for split-detector images from either device (MU: p = 0.86; MCW: p = 0.2), and MU confocal images (p = 0.14), but was significantly correlated for MCW confocal images (r = -0.2, p = 0.02; see Supplemental Figure 3).

Contrast was not significantly correlated for split-detector images from either device (MU: p = 0.72, MCW: p = 0.07), whereas confocal images from either device were significantly positively correlated (MU: r = 0.27, p = 0.002; MCW: r = 0.65, p < 0.001; see Supplemental Figure 4).

PIQE was not significantly correlated for MU confocal images (p = 0.09) but was positively correlated with average grade in split-detector images from both devices (MU: r = 0.31; MCW: r = 0.61, p < 0.001) and MCW confocal (r = 0.5, p < 0.001), indicating that images rated highly by graders were considered poor by PIQE, and vice-versa (see Supplemental Figure 5).

4. Discussion

We presented a fully automatic image quality metric for AOSLO images and assessed its performance across multiple AO devices and modalities. We demonstrated good agreement between human graders’ assessments of image quality and established that all three graders’ assessments of image quality were well correlated to our algorithm’s output. In addition, we compared this metric to other previously described metrics of image quality. While these properties make the algorithm effective for SNR estimation in AOSLO images, there are some limitations to this work that are important for accurate interpretation of these results.

To ensure that all graders were basing their judgements on similar image features, graders were given instructions to base their grades on the visibility of photoreceptors without explicit consideration for other retinal structures. However, as a whole-image analysis technique, our algorithm implicitly includes all periodic structures (beyond just photoreceptors), and it is unclear how well it will perform in images with less periodic features such as blood vessels. Future work will be needed to evaluate the algorithm performance under those conditions. We would expect that the algorithm would work well on strongly periodic structures such as RPE cells; however, any expansion to other non-periodic structures are likely to require substantial changes, or adaptation to a hybrid approach such as those used in the BIQI and PIQE metrics.

We also observed significant inter-modality SNR differences. Confocal images had significantly higher SNR values when compared to the split-detector images on the same device. This has been qualitatively observed in prior studies using split-detection, where the decrease in resolution compared to the confocal modality does not allow for the foveal cones and rods to be visible in some cases. An alternate explanation for this discrepancy could be that there is a substantial dynamic range difference present in confocal vs split-detector images, as we observed that on average, confocal images had a larger dynamic range than split-detector images (72.6 vs 54.3). To evaluate the impact of dynamic range on our algorithm, we systematically reduced the dynamic range to 75, 50, and 25% of our original ranges by increasing/decreasing the min and max values present in each image, respectively, and rescaling data over the new range. We observed that our algorithm was unaffected by reductions in dynamic range (see Supplemental Figure 7), implicating a real resolution difference as the source of the discrepancy between confocal and split-detector images.

Interestingly, we observed significant differences between the average grade of images with and without pathology. However, our SNR estimates showed a significant difference only in the confocal modality. This disagreement between subjective and objective assessments for only the split-detector modality may be due to assumptions underpinning our algorithm. It has been noted previously in subjects with photoreceptor-affecting pathologies that inner segments are often still visible in split detector [23,30] despite a widespread degeneration and dysflective outer segments [31]. As our algorithm is based in the Fourier domain, surviving inner segment structures would be discernable to the algorithm as increased signal whereas to graders there may not be enough contrast to suggest a higher quality.

We also found some surprising results. We found that image SNR across the two AOSLO designs was significantly different, despite human grades that were not significantly different. We would not expect this to arise from biased image selection, as all data was randomly obtained from prior datasets at both sites, implicating differences in system design or post-processing. The AOSLOs used in this study both broadly use the reflective afocal design published by Sulai et al [22], and differ principally in their light detectors and imaging sources. The AOSLO housed at MU uses avalanche photodiodes (APD) as light detectors, whereas the AOSLO housed at MCW uses photomultiplier tubes (PMT). For imaging illumination, the MU device uses an 850 ± 60 nm SLD, the MCW device uses a 775 ± 13 nm SLD. We do not expect the performance of the APT and PMT detectors to differ in this light regime [32]. However, we do expect differences in the spatial resolution of our images, as the Rayleigh criterion [33] indicates that the 775 nm source and 8 mm pupil used at MCW will provide superior resolution to MU’s 850 nm source and 7.5 mm pupil. This improved resolution does not appear to have a positive effect on SNR, as MU’s data on average exhibited higher SNR. This left post-processing as the most likely explanation for the difference. MCW’s image registration pipeline typically restricts the number of frames used during registration to 50 or less, whereas MU’s pipeline by default uses all frames with an NCC over a specified threshold. A post-hoc analysis of the number of frames averaged in MCW vs MU’s pipeline yielded a marked difference in numbers of averaged frames (MCW range: 20-80, MU range: 82-180). Given that we observe our algorithm to be sensitive to the classical relationship between averaged frames and SNR (Fig. 8), this is the most likely explanation for the discrepancy between the two sites.

We found that in most cases general purpose image quality metrics were inconsistent with our average grader and thus performed worse than the SNR-based approach we described here. However, what caused the inconsistencies varied from metric to metric. Surprisingly, the PIQE metric consistently rated images rated as a “5” as worse than images rated a “1” by graders, such that PIQE appeared to have an inverse relationship with image grade (see Supplemental Figure 5). We also compared the SNR and PIQE score in individual frames, and a similar inverse relationship appears to hold (see Supplemental Figure 6). The contrast metric was closest in performance to ours but was even more strongly sensitive to modality than our method (SNR worse case: 13% difference), exhibiting values that were substantially different (contrast worst case: 150% difference; Table 2). Like in our method, this is likely due to the implicit differences between confocal and split-detector images.

The algorithm is a good candidate for real-time feedback during an imaging session, exhibiting sensitivity to both poorly focused, noisy, and dim frames. At present, the algorithm is implemented in Python (version: 3.10) and still has an execution time of ∼0.25 seconds for an image size of 720 x720 pixels (a reference implementation provided in Code 1, Ref. [34]). The computer used in the development and testing of the algorithm contains a thirty-two logical core processor (AMD “Threadripper” 3955WX) with 32GB of RAM. Porting the algorithm to a compiled language such as C would make it feasible for analysis of images in real-time.

However, the algorithm is relatively insensitive to intra-frame motion as the SNR distribution of motion distorted frames overlaps fully with relatively undistorted frames (see Supplemental Figure 2). In each of the distorted images we assessed, image degradation was solely from eye motion, and as our algorithm operates by averaging DFT ROIs across the entire image, it is likely that any SNR loss due to distortion is mitigated by the presence of numerous higher quality ROIs. Future work will be required to add regional sensitivity to the algorithm.

5. Conclusion

No-reference, quantitative feedback on the usability of acquired images for processing and analysis is essential for efficient and effective use of AOSLO data and has potential to reduce the “chair time” not only for patients and subjects being imaged by these devices, but by the technicians and researchers responsible for analyzing them.

Taken together, these results have important implications for how clinical studies using AOSLO data are conducted. Often in these studies graders identify cells and report an ordinal measure of “confidence” in their identification; with this algorithm, images with SNR below a cutoff could be removed from consideration before the grader has even viewed the image. For this reason, we ultimately expect that this algorithm will lead to more reliable cell identifications.

Funding

Foundation Fighting Blindness10.13039/100001116 (CC-CL-0620-0785-MRQ); National Eye Institute10.13039/100000053 (F31EY033204, R01EY017607, R44EY031278, UL1TR001436); National Institutes of Health10.13039/100000002 (C06RR016511).

Disclosures

Cooper, R.F. has a personal financial interest in Translational Imaging Innovations. Research reported in this publication was supported in part by an Individual Investigator Award from the Foundation Fighting Blindness, award number CC-CL-0620-0785-MRQ, the National Eye Institute and the National Center for Advancing Translational Science of the National Institutes of Health under award numbers R01EY017607, F31EY033204, R44EY031278 & UL1TR001436. This investigation was conducted in part in a facility constructed with support from a Research Facilities Improvement Program, grant number C06RR016511 from the National Center for Research Resources, NIH. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.

Data availability

All images underlying the results are available in Dataset 1 ^{(122.1MB, zip)} , Ref. [24].

Supplemental document

See Supplement 1 ^{(1.7MB, pdf)} for supporting content.