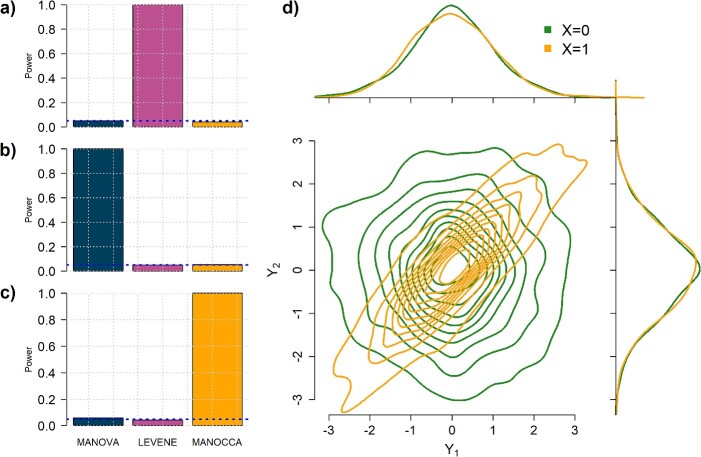
Figure 3.

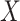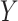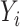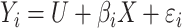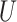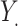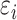Orthogonality between MANOCCA and other tests. We simulated a series of datasets under three models where a binary predictor influences orthogonally either the mean, the variance or the covariance of a bivariate outcome . In model (A), each outcome is drawn from a standard additive model: , where is a normally distributed variable shared across and are independent normal residuals. In model (B), each 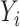is drawn from 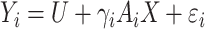, where 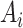is normally distributed variables producing heterogeneity in the variance of 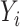conditional on 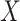. In model (C), each 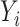is drawn from the interaction model 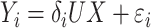, which produces heterogeneity in the correlation across 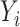conditional on 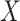. For each model, we derived the power at the P-value threshold of 0.05 for a joint mean effect test (MANOVA), a test of variance for a randomly selected 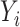(LEVENE) and the proposed covariance test (MANOCCA). The parameters 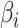, 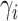and 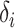were chosen to maximize the power of the at least one of the three tests. The dashed line indicates the P-value threshold of 0.05. (D) shows an example of a bivariate distribution where 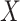is not associated with the mean and variance of the two outcomes but with their covariance.