Tailoring barrier layers design for haute couture through X-ray microanalysis: Insights and guidelines

Abstract

Barrier layers against intermetallic diffusion are a fundamental part on engineering electroplated coatings as they improve the lifetime of goods reducing wastes and improving the sustainability of the production chain. This study aims to set a cost-effective methodology to characterize barrier systems by evaluating the effectiveness with a recent approach based on XRF and EDS and characterize the kinetic of diffusion processes with X-ray diffractometry. Several high fashion barrier systems were tested highlighting that anticorrosion systems are not automatically suited as barrier layers for intermetallic diffusion, as opposed to industrial practice. Investigations on gold coatings obtained varying the current density revealed a correlation between the activation energy of the diffusion process, roughness, and crystallite size.

Graphical abstract

Highlights

• •EDS measurements are used for the determination of intermetallic diffusion.
• •Nickel and palladium are good barrier layers against copper-in-gold diffusion.
• •Contrary to popular belief, bronze is not useful as a barrier layer for copper.
• •Diffusion of tin into gold was also detected.

1. Introduction

The need to obtain surface-functionalised manufacts from thin and ultra-thin films of metallic material has increased drastically in recent years. This increase in demand is due to a multiplicity of factors as the scarcity of strategic metals [1] for the 4.0 industrial revolution and the uprising need for the energy transition from an oil-based to a hydrogen-based economy (as announced in “COP 21” by the European Union [2] and, more recently, with the deadline on selling CO₂ emitting cars in 2035 [3]). Within these changes, electroplating industries are on the front line to become more efficient and provide improved products to satisfy the increasing demand and reduce the usage of strategic metals (Nickel [4], Gold and Palladium [5]) mainly in non-essential fields such as the decorative industry [6]. Electroplated manufacts are more often composed of multiple phases to obtain the desired properties [7]. In decorative and electronic industries the combination of gold and copper is mandatory: the high conductivity of copper and its alloys is combined with the chemical inertness and aesthetic features of gold [8]; in haute couture¸ copper is not only present in the substrate (most commonly brass), but it is also electroplated due its levelling power to give the desired brightness and shine to the artifact [9]. The main problem related to Au–Cu systems is the intermetallic diffusion [10]. Intermetallic diffusion is a thermodynamically driven phenomenon that could bring changes in mandatory characteristics of the artifacts as corrosion resistance and colour, limiting the lifetime of products. This is especially true for high fashion because the lifetime of an accessory is not related to its functional properties, but it is dictated by the aesthetical aspect. The diffusion coefficient (D) is described by the Fick's first law (1) and D can be associated with an Arrhenius-like equation (2); passing in logarithmic scale (3), it is possible to see how the logarithm of D is directly proportional to the inverse of the temperature (T) and how the activation energy (E_act) of the diffusion process is the slope of the resulting function. It should be noted that the linearity of ln(D) with T⁻¹ it is verified only if E_act is constant, this condition is reached only if one diffusion process is happening in the examined temperature range.

$$F=-D\frac{dC}{dx}$$ (1)

$$D=D_0{e}^{\left(\raisebox{1ex}{$E_{act}$}\!\left/ \!\raisebox{-1ex}{$\left(RT\right)$}\right.\right)}$$ (2)

$$\ln \left(D\right)=\ln \left(D_0\right)-\frac{E_{act}}{RT}$$ (3)

There are two main intermetallic diffusion processes: lattice diffusion and grain boundary diffusion. Lattice diffusion occurs when diffusing species go through the crystalline lattice of the diffusion matrix [11] and phase shifts are observed in X-Ray Diffractometry (XRD) experiments; instead, in grain boundary diffusion, the process occurs through defects between grains [12]. To prevent intermetallic diffusion, additional electrodeposited phases called barrier layers are added to the Au–Cu system. The majority of electrodeposited barrier layers, in the decorative field, are made by Ni alloys (a toxic [13] and strategic element), Pd alloys (a strategic [14] and precious metal) or by highly cyanurate baths (like white bronzes) [15,16]. The knowledge of the effectiveness of a barrier layer (quantified by the diffusion coefficient of copper in the whole system) is fundamental to minimising the thicknesses of available barrier layers or to characterising novel solutions to reduce the usage of strategic metals and the environmental impact of electroplating plants to follow the guidelines of sustainable development set by United Nations (UN) 2030 Agenda [17]. To determine the diffusion coefficients of barrier layers various methods are being reported in literature, e.g., Auger Electron Spectroscopy (AES) [18], X-ray Photoelectron Spectroscopy (XPS) [19], Rutherford Backscattering Spectrometry (RBS) [20] and Secondary Ion Mass Spectrometry (SIMS) [12], but they all require costly equipment that are not commonly present in electroplating industries, effectively preventing the optimisation of production processes. A common test that is used in the decorative field is based on a colorimetric assay, where a sample is annealed at 180 °C and the colour difference in the CIE L*a*b colour space [21] is evaluated; this method, albeit inexpensive, is proven to be inaccurate and to give, at least, qualitative results. In a previous work we developed a novel methodology based on Energy Dispersive Spectroscopy (EDS) microanalysis and X-ray fluorescence, that has been able to determine the diffusion coefficients of Au–Cu electroplated systems [22]. This procedure seems to be the best candidate to be used as a cheaper and effective way to study barrier layers, especially in industrial fields. XRF is commonly used in almost every electroplating plant to measure the thickness of electrodeposited film [23] and desktop SEM equipped with EDS detector are present in analytical laboratories of galvanic products suppliers and, with the decreasing in cost of those instruments, they are also expected to increase the presence within the electroplating industries themselves.

The purpose of this work is to set the guidelines to develop and evaluate electroplated barrier systems against intermetallic copper diffusion in industrial samples, exploiting a new methodology that can, hopefully, become a quality standard test to optimize the processes of electroplating plants, reducing the embodied energy and environmental impact of artifacts, especially in the decorative field. In comparison, we performed colorimetric measurements, as they are the most used tests to evaluate barrier layers performances within haute couture industries. XRD measurements were carried on obtaining more information about the kinetics of diffusion processes involving barrier layers and to explain deviations from equation (3). The study was about commonly used barrier layers in the haute couture field as Nickel (Ni), Nickel–Phosphorus (NiP), Palladium–Iron (PdFe), Palladium–Nickel (PdNi) and White Bronze (WB). Then, additional evaluations were performed on two systems with Tin–Ruthenium as anticorrosion layer to determine if this alloy acts, also, as a barrier layer. Lastly, measurements on Au–Cu systems varying the deposition parameters and the use of a AuCo alloy layer which has previously exhibited barrier properties [22].

2. Materials and methods

2.1. Methodology to determine D

To evaluate the intermetallic diffusion the method proposed by Giurlani et al. [22] was employed and D was calculated as described in (4).

$$D=\frac{t_s·t_c}{T_p}=\frac{t_s·\left(t_b+t_t\right)}{T_p}$$ (4)

The mathematical treatment to arrive at this form has already been dealt with extensively by Tompkins et al. [24]. D is the diffusion coefficient, T_p is the time step between two measurements, t_s is the equivalent thickness of diffused species, and t_c is the thickness of the coating on top of diffusing species. t_s should not be taken as an indication of the formation of a homogeneous layer of diffused species, but as an approximation of the equivalent thickness of the diffused mass having bulk density; this approximation is fundamental for applying the Tompkins mathematical model cited before. The methodologies to determine all the t_x (x = s, c) are reported in the 2.2 subsection and extensively discussed in the presenting methodology paper [22]. In this work, specifically, to evaluate barrier layer performances, it is proposed to divide t_c in two terms: the thickness of the barrier system (t_b), and the thickness of the topcoat (t_t), which in this study is the thickness of the gold layer; in the case of AuCu samples t_c = t_t as t_b = 0. Activation energies were obtained from Arrhenius plots, fitting obtained diffusion coefficients with equation (3).

2.2. Samples preparation and characterization

The substrates used were mirror polished brass disks with a radius of 1.25 cm and the samples were kindly electroplated by Materia Firenze Lab Srl (FI, Italy) on its industrial production line according to internal standard production process: the commercial electroplating solutions employed were Bluclad© Bronze Titanium MUP for WB, Bluclad© 3000 MUP for Ni, Bluclad© 350 MUP for NiP, Bluclad© 720 PDFE MUP for PdFe, Bluclad© 1811 MUP for PdNi and Bluclad© 8670 MUP for AuCo. The pure gold bath (AURO 24©) used was kindly provided by Italfimet Srl (AR, Italy) and the SnRu bath (IMET©) was kindly provided by Valmet Plating Srl (FI, Italy). Prior to barrier layer and gold deposition, a thick layer of copper (>20 μm) was electroplated on every brass disk. Three different families of samples were made: AuCu, commonly used barrier layers (CBL), thin film solutions (TFS).

Every class of samples was annealed at four different temperatures (100 °C, 133 °C, 167 °C and 200 °C) for 100 h. The characterization was performed before and after this thermal treatment. Before putting the samples in the oven (Binder ED 115, equipped with an electronic temperature control system of ±1 °C) they were rinsed in acetone, ethanol, and water, and placed in a glass covered Petri dish to avoid any contamination by particles or dust inside the oven, although maintaining direct contact with the external environment not being air sealed.

Hitachi SU3800 (Tokyo, Japan) SEM equipped with an Oxford Instruments NanoAnalysis Ultim max 40 SDD was used to perform imaging, microanalysis and alloys composition. The SEM analyses were performed at an acceleration voltage of 5 kV and 300× magnification at the centre of the disks. To obtain the equivalent diffusion thickness of diffusing species migrated to the surface (t_s), the K-ratio method [25,26] was employed. It is a semiquantitative methodology based on calculated calibration curves that makes possible to measure nanometric and subnanometric thicknesses typical of diffused layers. EDS spectra of systems made of a variable thickness of copper or tin (0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.20, 2.5, 5.00 nm) on top of a bulk gold substrate were simulated with NIST DTSA-II Neptune [27,28], the calibration curves obtained from simulated spectra are reported in Figure A.1 and Figure A.2 (all Figures A.x are reported in Appendix A as Supporting Information). The settings of the simulations were 5 kV accelerating voltage and 32‧10³ electrons. To estimate errors, the uncertainty of K-ratio given by the instrument, and obtained by applying the Poisson distribution, was propagated. The compositions of deposited barrier layers were obtained thanks to EDS measurements at 5 kV on samples without the gold coating.

X-ray fluorescence (XRF) thickness determinations, based on Fundamental Parameters (FP) methodology, of gold and barrier systems (t_c) were performed with a Bowman BA-100 XRF spectrometer (Schaumburg, IL, USA). The accelerating voltage was set to 50 kV and the tube current to 0.8 mA. A 0.5 mm filter of aluminium and a collimator of radius equals to 0.3 mm were employed. All the measurements were collected at the centre of the samples with an integration time equal to 60 s.

All XRD diffractograms were collected at CRIST Centre, University of Florence (Florence, Italy) using a Bruker (Billerica, MA, USA) New D8 Da Vinci (Cu-Kα radiation = 1.54056 Å, 40 kV × 40 mA), equipped with Euler cradle for massive samples and 'Bruker LYNXEYEXE' detector. The scans were performed in a range of 2θ = 25°–100°, with 2θ = 0.05° increment and 0.05 s of integration per step. Peak identification was performed by comparing the obtained spectra within the ICDD (Newtown Square, PA, USA) PDF-4+ 2021 [29] database. The size of Au crystallites from FWHM (full width at half maximum) [30] of AuCu samples was obtained by processing diffractograms with DIFFRAC.TOPAS [31], performing a Pawley refinement [32].

Roughness on AuCu samples was evaluated with Atomic Force Microscopy (AFM) using a Molecular Imaging PicoSPM (10 μm × 10 μm, 512 px × 512 px, 1 lines/s speed) equipped with a non-conductive Veeco NP-S10 silicon nitride triangle-shaped cantilever (spring constant of 0.12 nN per meter). The measurements were done in contact mode with a force setpoint of 0.5 V.

2.2.1. AuCu

Three different sets of AuCu samples were electroplated: “Low”, “Normal” and “High”. After the copper electrodeposition a gold layer of about 0.3–0.5 μm was electroplated varying the current density. “Normal” were made with standard deposition parameters used for TFS and CBL samples, as 0.5 A‧dm⁻² is the optimal current density according to the bath supplier.

2.2.2. Commonly used barrier layers (CBL)

Ni, NiP, PdNi, PdFe and WB were selected because they are the most common barrier layers used in the fashion field. The industrial procedure followed by the electroplating company involved the deposition of the barrier system (0.3–0.5 μm) and the deposition of a gold layer (0.3–0.5 μm). The composition of deposited barrier layers, obtained from EDS analysis, are reported in Table 2.

Table 2.

CBLs composition reported in wt%.

Barrier Layer	Composition
Ni	Ni 100 wt%
NiP	Ni 87 wt%; P 13 wt%
PdNi	Pd 89 wt%; Ni 11 wt%
PdFe	Pd 95 wt%; Fe 5 wt%
WB	Cu 46 wt%; Sn 40 wt%; Zn 14 wt%

2.2.3. Thin film solutions (TFS)

SnRu//PdFe, SnRu and AuCo (high carat gold-cobalt >23.5 kt) were selected as thin film barrier layers. The industrial procedure used to obtain SnRu and AuCo samples involved a flash deposition (0.02–0.1 μm) on the copper-coated brass disks followed by the deposition of a gold layer (0.3–0.5 μm). SnRu//PdFe samples were obtained by electroplating a layer of PdFe (<0.1 μm) between the SnRu layer (<0.1 μm) and gold one (0.3–0.5 μm). The composition of SnRu and AuCo alloys, is reported in Table 3.

Table 3.

Alloys composition of barrier layers used for TFS samples reported in wt%.

Barrier Layer	Composition
SnRu	Sn 85 wt%; Ru 15 wt%
AuCo	Au 99 wt%; Co 1 wt%

3. Results and discussion

3.1. Cu intermetallic diffusion

3.1.1. AuCu

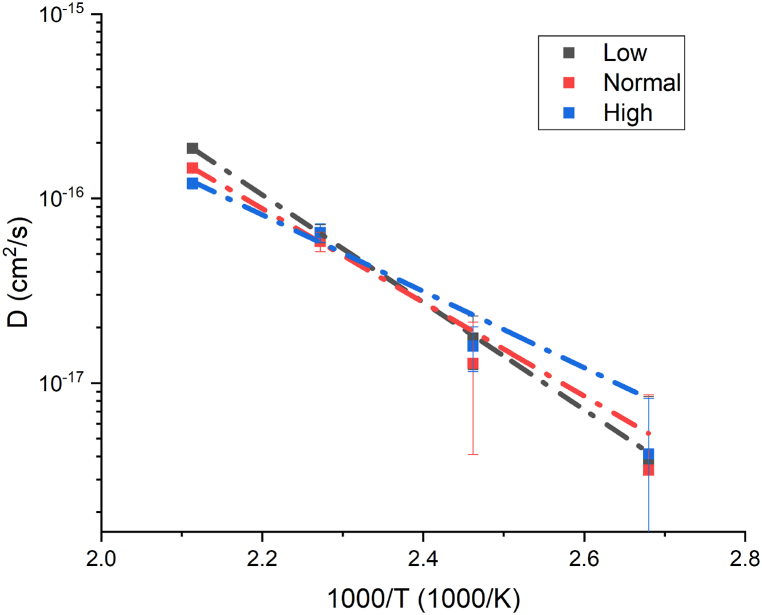
Gold layer thicknesses (t_c) were obtained by XRF measurements and are reported in Table A.1 (all Table A x are reported in Appendix A as Supporting Information) as well as t_s calculated by EDS analysis. AuCu samples diffusion coefficients obtained by the previously described method are shown in Table 4; the activation energy was extracted by the slope of data shown in Arrhenius plot (Fig. 1), obtained by fitting the diffusion coefficients with equation (3). As it can be appreciated in Table 5 the activation energy differs from the three samples, with a reverse trend compared to the current density value used for electrodeposition (Table 1) and described in section 2.1.1.

Table 4.

Determined diffusion coefficients of AuCu sample.

Temperature (°C)	Diffusion coefficient cm2·s−1 ( × 1017)
	High (0.8 A‧dm−2)	Normal (0.5 A‧dm−2)	Low (0.25 A‧dm−2)
100	0.4 ± 0.5	0.3 ± 0.5	0.4 ± 0.5
133	1.5 ± 0.6	1.3 ± 0.6	1.7 ± 0.6
167	6.5 ± 0.7	5.9 ± 0.7	6.5 ± 0.7
200	12 ± 0.8	15 ± 0.9	19 ± 1

Fig. 1.

Arrhenius plots, related to Cu diffusion, of AuCu samples.

Table 5.

Activation Energy and Au crystallite dimensions or AuCu samples.

	Eact (KJ/mol)	Roughness RMS (nm)	Au crystallite dimensions (nm)
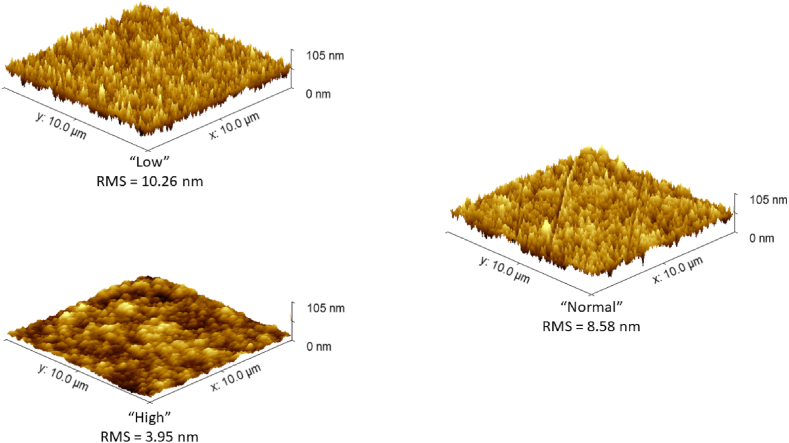
High	40 ± 6	3.95	39.2 ± 0.8
Normal	49 ± 2	8.58	36.3 ± 0.7
Low	56 ± 0.4	10.26	32.1 ± 0.7

Table 1.

Current densities employed to deposit AuCu samples.

Samples	Current density (A‧dm−2)
Low	0.25
Normal	0.5
High	0.8

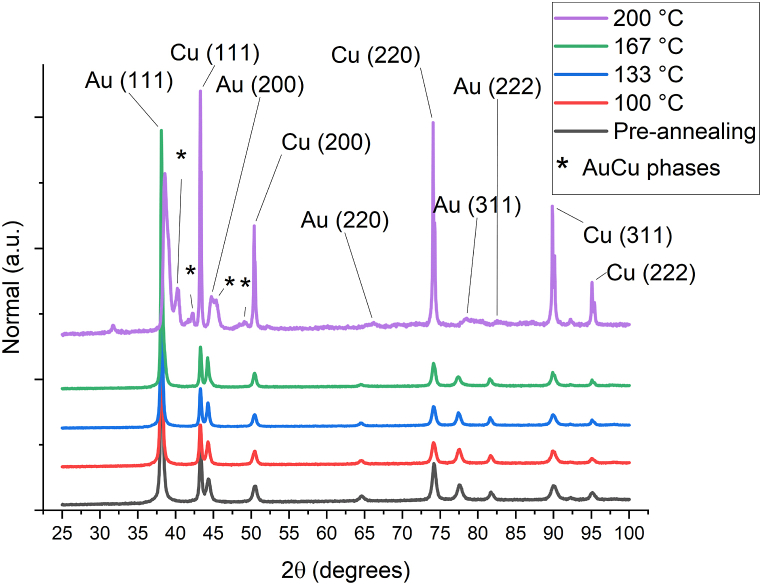
The differences between activation energies can be explained by a different structure of the gold coating [24] in function of the current density: Omura et al. [33] reported that the microstructure of electroplated gold can be tuned by varying the current density. This is especially true if grain boundary diffusion is the main mechanism; the linearity of Arrhenius plot is a strong indicator that one diffusion mechanism is predominant. To confirm that grain boundary diffusion was the prevalent diffusion mechanism, a comparison was done between diffractograms taken before and after different annealing temperatures on the “Normal” samples (low and high samples diffractograms follow the same behaviour and are reported for completeness in Figure A.3 and Figure A.4). In Fig. 2 it can be observed that only at temperature equal to 200 °C there is the presence of mixed Au–Cu phases, this means that lattice diffusion starts only at temperature above 167 °C but it remains negligible in comparison to grain boundary diffusion, as it is reported in literature [18] and confirmed by the Arrhenius plot.

Fig. 2.

Comparison between diffractograms taken before different annealing temperatures on "Normal" AuCu samples; It can be observed that only at the temperature of 200° there is the formation of Au–Cu mixed phases.

From AFM imaging (Fig. 2) mean quadratic roughness (RMS) was collected, and then from profile fitting of diffractograms taken before the annealing, the FWHM crystallite size was extrapolated (Table 5).

The results obtained showed that a smaller crystallite dimension is associated with a high roughness and with high E_act. From Fig. 3 it can be observed how from “High” to “Normal” there is an important change in the morphology of the microstructure, as lower current densities seem to lead towards more packed conical structures of lower overall dimensions as evidenced by the size of the crystallites. Then trend of roughness towards current density is in agreement with what is reported in the literature [34,35] for this range of current densities; hence the morphology should be addressed as the influencing factor of E_act.

Fig. 3.

AFM images obtained on AuCu samples; the RMS roughness is reported.

As grain boundary diffusion was verified to be the predominant diffusion mechanism in the examined temperature range and considering that the grain boundary diameter is a determinant factor for E_act¹², then the dependency between E_act and crystallite size can be explained by a decrease of boundary widths [36] as crystallites of a smaller size are closely packed [37,38], making it more energy-intensive for the diffusing species to pass through the them [10]. Also for electrodeposited metals a good agreement has been reported between the crystallite and grain sizes [39,40]. Therefore, the design of barrier systems should consider deposition methods that can heavily tailor crystallite size and morphology like pulsed current deposition [41].

3.1.2. CBLs

CBLs had good performances except for WB, the only non-precious non-nickel layer (Table 6). The thicknesses of barrier (t_b) and gold layers (t_t) obtained by XRF measurements are reported in Table A.2 as well as equivalent diffused copper layer (t_s) evaluated by EDS. The equivalent diffused layer of copper was under the detection limit (no EDS signal was detected for Cu L) for almost all non-WB samples but for Pd alloys annealed at 200 °C. For those samples D was below the quantification limit as the error was greater than the measured value. The slightly better performance of Ni-alloys compared to Pd-alloys agrees with what is found in the literature [42].

Table 6.

Intermetallic diffusion coefficients of copper for CBL samples.

Temperature (°C)	Diffusion coefficient cm2·s−1 ( × 1017)
	100 °C	133 °C	167 °C	200 °C
NiP	n.d.	n.d.	n.d.	n.d.
Ni	n.d.	n.d.	n.d.	n.d.
PdNi	n.d.	n.d.	n.d.	0.003 ± 0.3
PdFe	n.d.	n.d.	n.d.	0.006 ± 0.3
WB	0.3 ± 0.1	11 ± 2	36 ± 0.3	45 ± 0.3

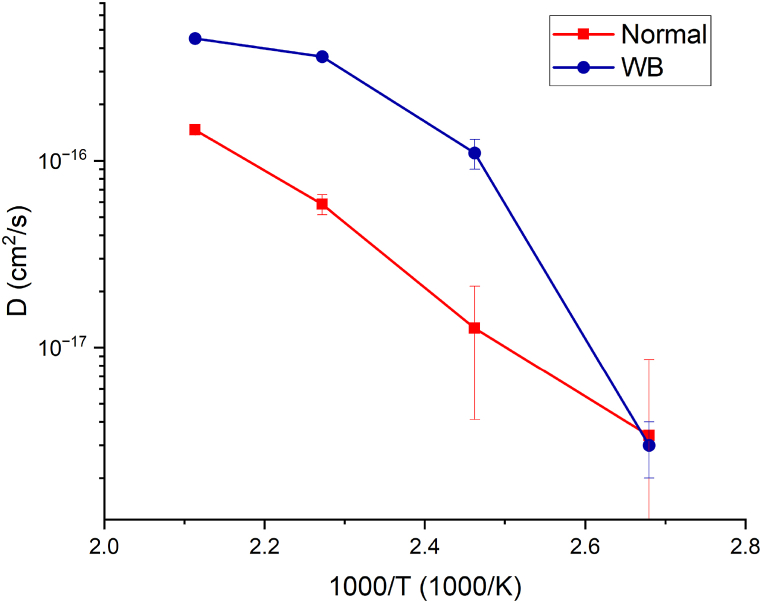
Arrhenius plot of WB is compared to a system without a barrier layer (AuCu “normal”) in Fig. 4: it is not linear and, more important, the diffusion coefficient is higher than the system without a barrier layer for T = 133 °C, 167 °C and 200 °C. A non-linearity in the Arrhenius plot indicates a change in the main diffusion mechanism as it is related to a different E_act in equation (3).

Fig. 4.

Comparison between Arrhenius plots, related to Cu diffusion, of Normal AuCu and white bronze barrier system.

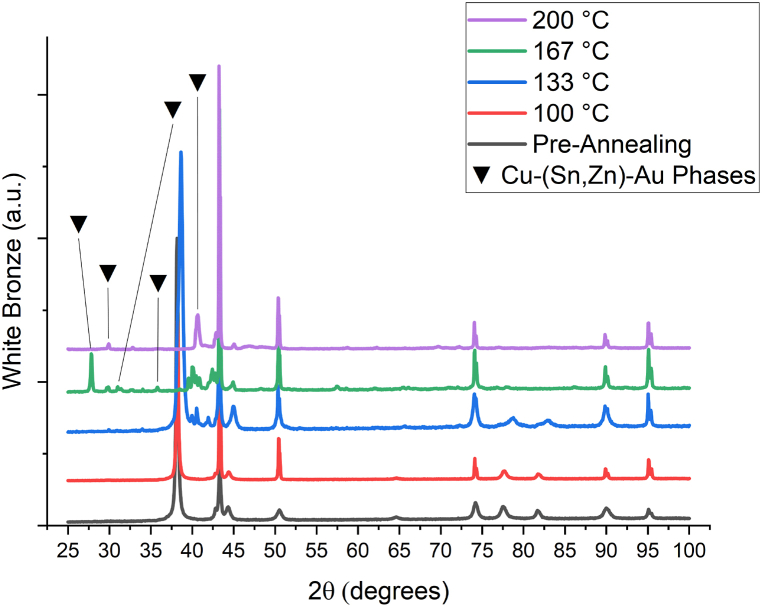
This behaviour can be clarified by XRD measurements [42,43]: as shown in Fig. 5 the annealing at temperature higher than 100 °C caused a phase transition as it evidenced by the disappearing of the Au (111) peak at 38° and appearing of peaks in the 40°–45° range. As stated in the introduction a change in phases is typical of lattice diffusion; this, in conjunction with the curvature of the Arrhenius plot, is a strong indication of the change in the main diffusion mechanism; In that it appears to have shifted from a kinetics governed by grain boundary diffusion to one governed by lattice diffusion [11].

Fig. 5.

Comparison between XRD diffractograms of WB samples; the annealing at 166 °C and 200 °C led to a phase transition as evidenced by the disappearing of Au (111) peak at 38° and Cu (111) peak at 43°.

This peculiar trend of WB to switch diffusion mechanism from grain boundary to lattice diffusion makes it unsuitable for artifacts that must withstand thermal stress; in particular, the use of this barrier system for finishes involving cataphoresis is not recommended, as such processes are often conducted at high temperatures [44,45]. No significant changes correlated with annealing temperatures has been observed in diffractograms of other CBLs, those are reported in Figure A.5 (NiP), Figure A.6 (PdFe), Figure A.7 (PdNi) and Figure A.8 (Ni).

3.1.3. TFSs

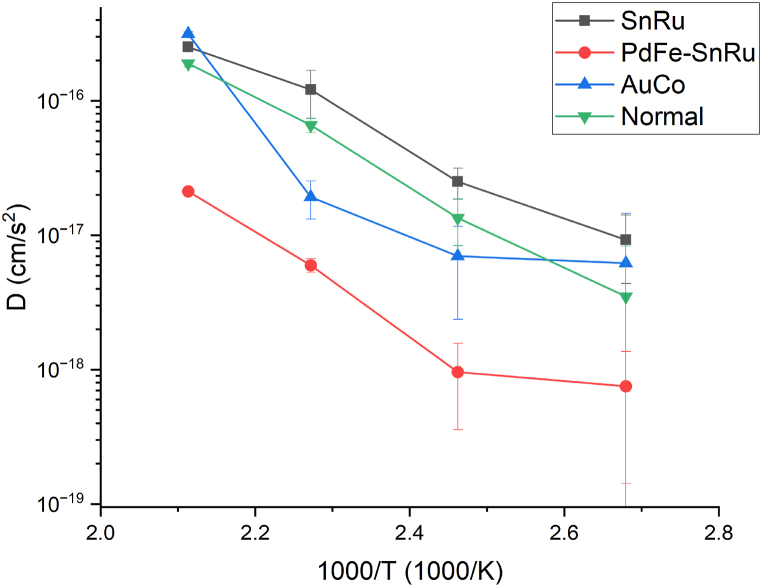
Copper diffusion coefficients of TFSs samples are shown in Table 7, the measured thicknesses of barrier and gold layers are reported in Table A.3. From the Arrhenius plot (Fig. 6) it can be appreciated as SnRu, despite being a widely used anticorrosion layer, preventing the oxidation of the substrate from atmospheric agents, is not a barrier layer towards the copper intermetallic diffusion. Hence, the proved barrier effect of the PdFe–SnRu system is mainly attributable to the PdFe layer.

Table 7.

Intermetallic diffusion coefficients of copper for TFSs samples.

Temperature (°C)	Diffusion coefficient cm2·s−1 ( × 1017)
	100 °C	133 °C	167 °C	200 °C
AuCo	0.6 ± 0.8	0.7 ± 0.5	2.0 ± 0.6	31 ± 1
SnRu	0.9 ± 0.5	2.5 ± 0.6	12 ± 5	25 ± 1
PdFe–SnRu	0.08 ± 0.06	0.10 ± 0.06	0.60 ± 0.07	2.12 ± 0.07

Fig. 6.

Comparison between Arrhenius plots, related to Cu diffusion, of Normal AuCu and TFSs samples.

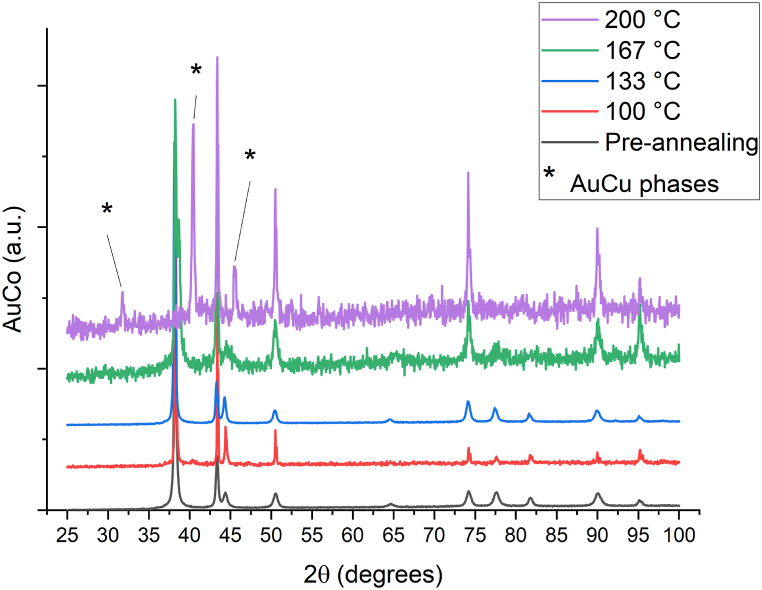
AuCo samples have not a linear Arrhenius plot (D at 200 °C is not linear with the other points, even considering the error bars), this like the WB case, is due a changing in the main diffusion mechanism as confirmed by XRD experiments (Fig. 7). In the diffractogram of the sample annealed at 200 °C there is no Au(111) peak at 38° and peaks attributable to AuCu phases at 32°, 41° and 46° are present. The trend of the other three points (100 °C, 133 °C, 167 °C) confirms what was observed in the previous work [22] i.e. a less steep, compared to AuCu, Arrhenius plot for Au//AuCo//Cu systems. Diffractograms of SnRu and PdFe–SnRu samples are reported in Figure A.9 and Figure A.10, no appreciable changes in phases were observed, confirming that only grain boundary diffusion occurs at least until 200 °C.

Fig. 7.

Comparison between XRD diffractograms of AuCo samples; the annealing at 200 °C led to a phase transition as evidenced by the disappearing of Au (111) peak at 38° and the appearing of peaks related to AuCu phases.

3.2. Sn intermetallic diffusion

Sn intermetallic diffusion was observed in WB (Cu 46 % Sn 40 % Zn 14 %) and SnRu (Sn 85 % Ru 15 %) samples (Table 8); t_t, and t_s are reported in Table A2 for WB and Table A3 for SnRu, t_b is equal to 0 because the Tin release is from the barrier layer itself.

Table 8.

Intermetallic diffusion coefficients of tin for TFSs samples.

Temperature (°C)	Diffusion coefficient cm2·s−1 ( × 1017)
	100 °C	133 °C	167 °C	200 °C
WB	0.2 ± 0.2	1.6 ± 0.2	5.4 ± 0.3	4.3 ± 0.3
SnRu	1.0 ± 0.4	1.2 ± 0.4	2.0 ± 0.6	1.3 ± 0.4

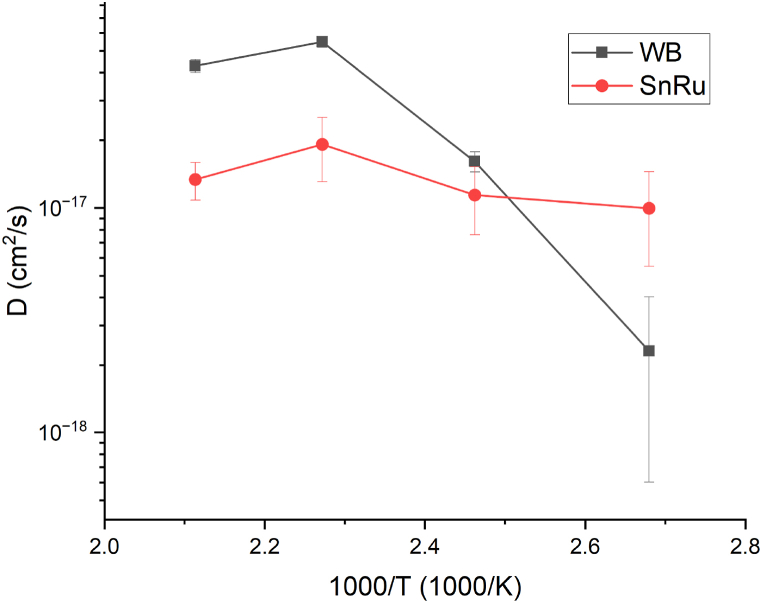
From the Arrhenius plots (Fig. 8) is observable as WB has a minor release of tin at lower temperatures, but already at 133 °C degrees the trend is reversed, confirming the inadequacy of the WB as an anticorrosion or barrier layer for artifacts that undergo thermal treatments. On the other hand, SnRu tin release is only mildly temperature dependent, and better suited as an anticorrosion layer if coupled with a good barrier layer. No tin release was observable in PdFe–SnRu systems, highlighting the excellent barrier capabilities of PdFe even against tin.

Fig. 8.

Comparison between Arrhenius plots, related to Sn diffusion, of SnRu and WB systems.

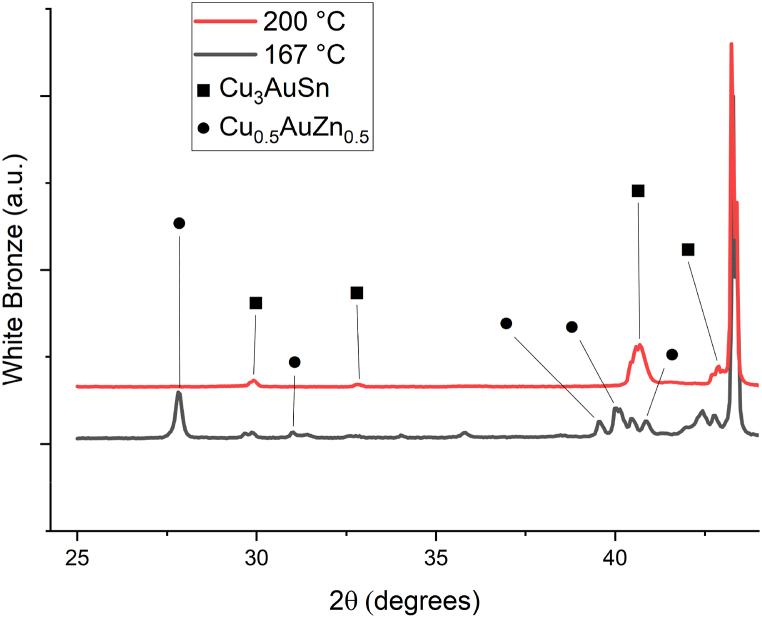
The odd behaviour of WB Arrhenius plot that loses linearity for the sample annealed at 200 °C is explained by a phase transition between 167 °C and 200 °C from orthorhombic Cu0.5AuZn0.5 [46] to cubic Cu3AuSn [47]. What it probably happens is that the diffused tin layer on top of the diffusion Au matrix, at the temperature of the phase transition, starts to migrate back to form the Cu–Au–Sn ternary alloy. It can explain why D at 200 °C is lower than D at 167 °C even considering the error bars Fig. 9.

Fig. 9.

Comparison of XRD diffractograms of WB samples annealed at 167 °C and 200 °C; A phase transition from Cu0.5AuZn0.5 to Cu3AuSn occurs between 167 °C and 200 °C.

4. Conclusions

An innovative and cost-effective methodology to determine intermetallic diffusion coefficients was applied to study the influence of morphology and crystallite size on D and to study the performances and behaviours of multiple barrier systems. Diffusion coefficients of Cu in different matrices as low as 10¹⁸ cm²/s were successfully quantified; tin release from barrier layers and the relative Sn diffusion coefficients in Au matrix as low as 3·10¹⁸ cm²/s were also successfully quantified.

The predominant diffusion mechanism of each system was investigated through Arrhenius plots and XRD experiments: changing in the main diffusion mechanism, from grain boundary to lattice diffusion, within the examined temperature range, was observed for AuCo and WB systems and in both cases led to a decline in barrier layer performance. WB as the main anticorrosion and barrier layer in nickel-free electroplating cycles performed poorly compared to others, especially at higher temperatures, which makes this material unsuitable for procedures involving heat treatments such as cataphoresis. The speculation about SnRu anti-corrosion layer as a barrier layer proved incorrect and its usage has to be done in combination with a barrier layer such as PdFe. SnRu tin release resulted only mildly dependent on temperature which makes it a better choice, as an anti-corrosion layer, than WB if thermal treatments are required; it was also demonstrated the capability of PdFe in stopping Sn diffusion. From the comparison between data obtained from CBLs and TFSs is clear that this method benefits from much lower thicknesses with respect to industrial standards. since D is independent of the barrier layer thickness, this allows annealing times to be kept short and it permits to reduce waste in R&D phases.

The results obtained on AuCu systems clearly demonstrate that, in the grain boundary diffusion regime, crystallite size and morphology influence heavily the activation energy of the diffusion process. This can give new direction and boost to the study of electrodeposited barrier layers, especially when coupled with pulsed current deposition techniques that allow greater control over the deposited material.

CRediT authorship contribution statement

Fabio Biffoli: Writing – original draft, Investigation, Data curation. Walter Giurlani: Writing – review & editing, Supervision, Methodology. Mariya Vorobyova: Writing – review & editing. Irene Maccioni: Writing – review & editing. Claudia Giovani: Writing – review & editing. Manuel Salvi: Writing – review & editing, Resources. Elisabetta Cianfanelli: Writing – review & editing. Marco Pagliai: Writing – review & editing, Supervision. Massimo Innocenti: Writing – review & editing, Supervision, Funding acquisition.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: