Performance reserves in brain-imaging-based phenotype prediction

SUMMARY

This study examines the impact of sample size on predicting cognitive and mental health phenotypes from brain imaging via machine learning. Our analysis shows a 3- to 9-fold improvement in prediction performance when sample size increases from 1,000 to 1 M participants. However, despite this increase, the data suggest that prediction accuracy remains worryingly low and far from fully exploiting the predictive potential of brain imaging data. Additionally, we find that integrating multiple imaging modalities boosts prediction accuracy, often equivalent to doubling the sample size. Interestingly, the most informative imaging modality often varied with increasing sample size, emphasizing the need to consider multiple modalities. Despite significant performance reserves for phenotype prediction, achieving substantial improvements may necessitate prohibitively large sample sizes, thus casting doubt on the practical or clinical utility of machine learning in some areas of neuroimaging.

In brief

Schulz et al. shed light on the role of sample size and imaging modalities in predicting cognitive and mental health traits from brain images. They underscore the potential of multimodal imaging to boost accuracy and caution about the challenges in achieving practical utility despite increasing sample sizes.

Graphical Abstract

INTRODUCTION

Advances in neuroimaging have provided unprecedented insight into the structure and function of the human brain. Concurrently, high-resolution brain scans have become increasingly cost effective and have raised hopes for automated disease diagnoses and clinical endpoint prediction based on neuroimaging data. Significant progress has been made in some areas of application, for instance in the automated detection of brain atrophy^1–3 and the segmentation of brain lesions.^4,5 However, the prediction of cognitive and behavioral phenotypes and the diagnosis of psychiatric diseases has remained challenging.^6,7 The main question that arises is whether these challenges in neuroimaging-based phenotype prediction are primarily due to insufficient sample sizes or a lack of predictive information in neuroimaging data.

Moving from group-level inference to accurate single-subject prediction and searching for intricate patterns in high-dimensional data can require sample sizes that are orders of magnitude larger than those of traditional neuroimaging studies.^8,9 Indeed, neuroimaging datasets have continuously grown in sample size over the last decade.¹⁰ While early neuroimaging studies were limited to only tens of participants, researchers now often include hundreds of participants aggregated from multiple acquisition sites. Large-scale data collection initiatives have grown from the Human Connectome Project,¹¹ with roughly 1,000 participants, to the UK Biobank’s Imaging Initiative,^12,13 with currently 46,000 participants and an end goal of 100,000 participants. Other researchers have proposed the Million Brains Initiative to facilitate precision medicine in the USA.¹⁴ Considering the significant resources required to collect large neuroimaging datasets, it is essential to determine the necessary sample size for reliable single-subject prediction of cognitive and behavioral phenotypes from brain images.

At the same time, there exists some controversy about how much predictive information can plausibly be extracted from conventional neuroimaging data. While high prediction accuracy has been reported for some phenotypes (overview in Arbabshirani et al.⁸), these findings have generated controversial debate,^7,15–18 and reliable neuroimaging biomarkers for psychiatric disease remain elusive.^6,7,19 High researcher degrees of freedom combined with imperfect model validation practices may have inflated results in small-sample studies.^15,20 In line with this hypothesis of overly optimistic reporting, meta-analyses have shown a pronounced inverse trend between prediction accuracy and sample size.²¹ Even under ideal circumstances, it is unclear to what extent intricate cognitive or behavioral traits can be predicted based on brain images.^7,22 Conventional neuroimaging could operate at suboptimal levels of abstraction or spatiotemporal resolution.^22,23 Moreover, neuroimaging is particularly affected by high levels of noise in the data (e.g., in functional magnetic resonance imaging [MRI] where the phenomenon being studied often only makes up a small part of the blood-oxygen-level-dependent signal^24,25) and in the target labels (e.g., inherent subjectivity of symptoms, low retest reliability of diagnoses^26–28). A lack of predictive information in the data or high levels of noise can pose an upper limit to the prediction accuracy, even in the limit of infinite samples and perfect machine learning algorithms. This raises the following question: do structural and functional brain images contain enough exploitable predictive information to be useful for precision medicine?

The two questions of sample size and exploitable predictive information are closely related. If there was insufficient predictive information in the data, then adding more participants would not improve prediction accuracy, and there would be no need for a Million Brain Project. Conversely, if we find that increasing the sample size yields continuous improvements in predictive accuracy, then we can conclude that we have not yet exhausted the predictive information contained in the data, and there is hope for accurate single-subject prediction. Therefore, it is crucial to clarify whether low prediction accuracy in a small- or medium-sized study primarily reflects fundamental limitations on predictive information (related to the so-called irreducible error, independent of sample size) or whether accuracy can be improved by increasing the sample size. This leads us to ask the following: can we mathematically characterize the empirical relationship between sample size and achievable prediction accuracy−the “learning curve”−for a given target phenotype? Characterizing and extrapolating such scaling laws would answer both original questions: it would provide estimates of the necessary sample size to reach a certain accuracy level as well as estimates of the highest achievable accuracy for a target phenotype given infinite samples.

Theoretical results from statistical learning theory state that the prediction accuracy typically scales as a power-law function of the sample size.^29–32 Empirically, power-law scaling of learning curves has been shown for models ranging from linear estimators to deep neural networks.^33,34 Hence, estimating power-law parameters from an empirical learning curve allows one to extrapolate the learning curve beyond the available sample size and thereby to delineate two key properties of the given prediction task: first, the convergence point of the learning curve represents the maximally achievable prediction accuracy. This can be taken as an estimate (technically a lower bound; see discussion) of the exploitable predictive information encoded in the data. Second, the speed of convergence can be defined as the sample efficiency, i.e., the amount of data needed by the model to learn the task. Intuitively, the former represents the ease of making accurate predictions, while the latter reflects the ease of learning how to predict. For a given brain imaging modality and phenotype, the power-law-scaling behavior of the learning curve should allow one to infer both the maximally achievable prediction accuracy and the necessary sample size to achieve clinically useful performance, thus quantitatively addressing two core aspects of feasibility for precision medicine.

In sum, deriving realistic estimates of achievable prediction accuracy and required sample sizes is crucial to gauge whether a predictive modeling approach may be suitable for single-subject prediction in precision medicine. Here, we systematically evaluate learning curves for different neuroimaging data modalities (structural and functional MRI) and a diverse set of demographic, cognitive, behavioral, and mental health phenotypes. We assess the validity of extrapolated learning curves and analyze which representations of brain imaging data have the highest predictive potential when considering large sample sizes and thus delineate areas of feasibility and infeasibility in the landscape of machine-learning-enabled predictions in precision medicine.

RESULTS

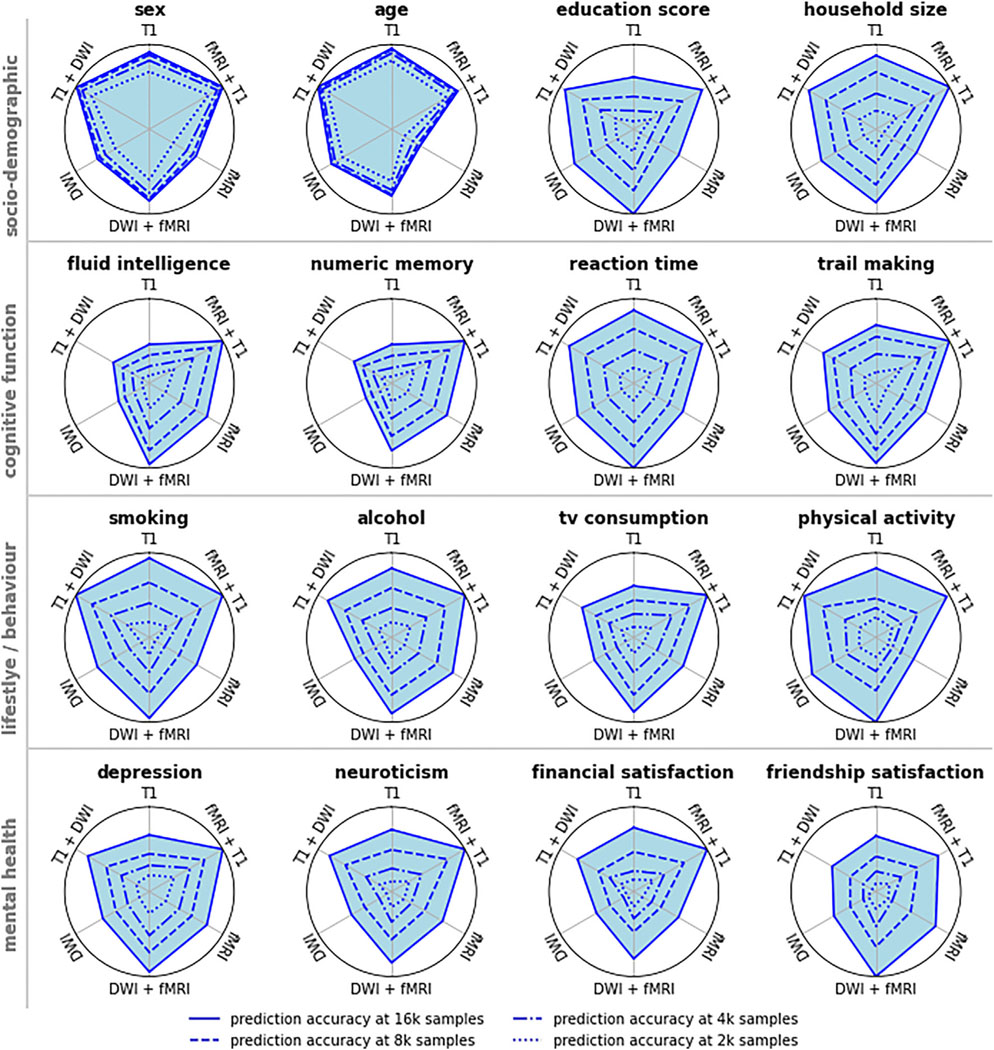
We based our analyses on the UK Biobank brain imaging dataset, which is the largest uniformly acquired brain imaging dataset available to date (46,197 participants, June 2021 release).¹³ Given its scope and extensive quality control, we argue that the UK Biobank can be considered a current “best-case scenario” for the upper end of available neuroimaging data analysis (see page 10 of the supplemental information for caveats regarding data quality). The UK Biobank provides imaging-derived phenotypes (IDPs) of T1-weighted structural brain MRI (regional gray and white matter volumes, cortical thickness and surface area), resting-state functional brain MRI (rfMRI; ICA-based functional connectivity), and diffusion-weighted imaging (DWI; anisotropy and diffusivity measures). From these IDPs, we predicted widely studied phenotypes from sociodemographic (age, sex, education score, household size); cognitive (fluid intelligence, reaction time, numeric memory, trail making); behavioral (alcohol, tobacco, and TV consumption, physical activity); and mental health (financial and friendship satisfaction, depression, neuroticism) domains. We used regularized linear models to predict target phenotypes from brain imaging data. Such models are considered highly competitive in the analysis of neuroimaging data and performed on par with more complex nonlinear models on similar prediction tasks.^9,35–37 To derive rigorous learning curves for our prediction scenarios, we repeatedly pulled smaller subsamples from the UK Biobank data (n = 256, 362, 512,…, 32,000) and trained and evaluated our models for each combination of sample size, input modality, and target phenotype. For each resulting learning curve, we fitted a standard power law [α n^−β + γ] to the empirical measures (cf. Hutter³² and Cortes et al.³³). For details on brain imaging data, target phenotypes, machine learning models, and evaluation procedure, please refer to the STAR Methods.

Learning curves follow power laws

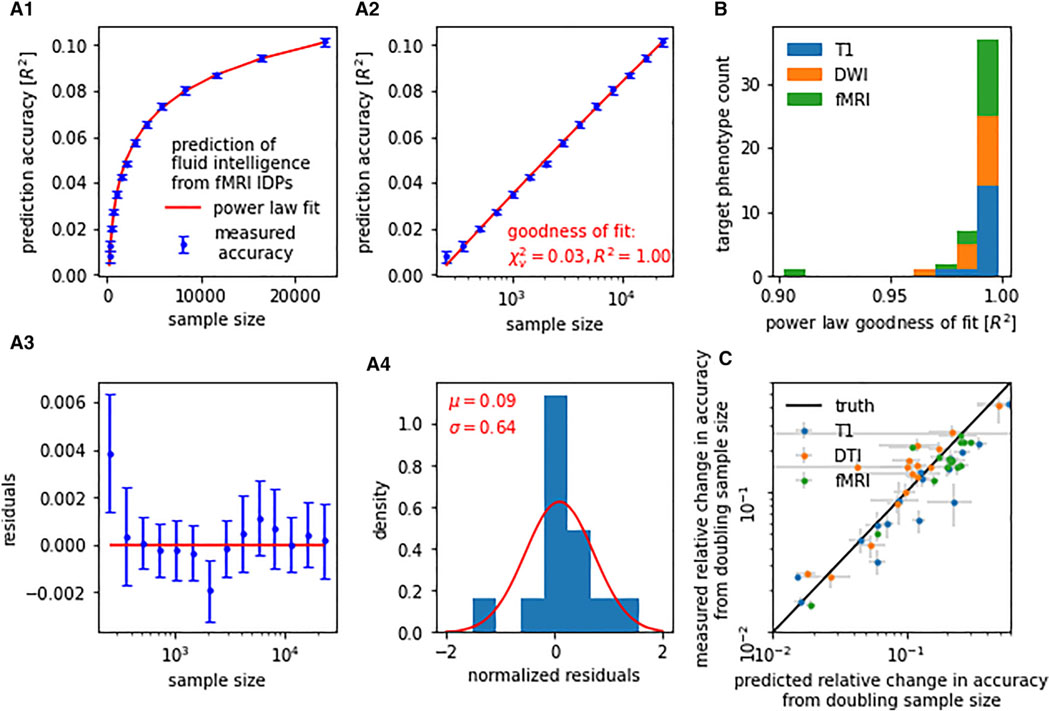
To assess how accurately the power-law function family describes learning curves for neuroimaging-based phenotype prediction, we calculated goodness-of-fit statistics (R², χ²) for each of the 48 (16 target phenotypes × 3 modalities) prediction tasks. An average coefficient of determination R² of 0.990 (SD = 0.015, minimum [min] = 0.902) indicated an excellent fit between power law and empirical learning curves (Figure 1). Reduced χ² statistics, on average 0.035 (SD = 0.038, maximum [max] = 0.207), were fully compatible with our power-law hypothesis. Note that χ² <<1, suggesting that our estimated measurement uncertainties were rather conservative.³⁸ Average goodness-of-fit statistics were comparable between imaging modalities (T1 R² = 0.994, rfMRI R² = 0.986, DWI R² = 0.991) and target-phenotype categories (sociodemographic R² = 0.993, cognitive R² = 0.996, behavioral R² = 0.982, mental health R² = 0.992). The observed scaling behavior of prediction accuracy with increasing sample size closely followed a power law for all investigated target phenotypes and imaging modalities.

Figure 1. Learning curves for neuroimaging-based phenotype prediction precisely follow a power-law function.

(A) Prediction accuracy scales with the number of training samples. The precise nature of this relationship can be described by a simple power law [α n^−β + γ]. (A.1) For instance, when predicting fluid intelligence from rfMRI data using ridge regression, out-of-sample accuracy (blue) closely followed the fitted power law (red). (A.2) We observed stable and continuous improvements in accuracy with increasing sample size, i.e., approximately linear scaling of prediction accuracy with log(n). (A.3 and A.4) Residuals of the power-law fit gave no indication of systematic deviations between measured accuracy and fitted power law.

(B) Power-law scaling was observed in all evaluated prediction tasks (i.e., combinations of imaging modality and target phenotype), with a goodness-of-fit R² between measured learning curve and power law of on average 0.990 (SD = 0.015, min = 0.902).

(C) Learning curve extrapolation predicted accuracy achievable on unseen larger samples. Shown are projected gains in prediction accuracy derived from learning curve extrapolation on the y axis in relation to observed gains in prediction accuracy on the x axis. Both were derived by doubling the training sample size from 8,000 to 16,000. Error bars indicate standard error of the mean (SEM).

Once a power law had been fitted to a learning curve, the curve could be mathematically extrapolated beyond the available sample size. To validate the results of such extrapolations, we fitted our power laws exclusively on sample sizes of 256 to 8,000, retaining the doubled sample size of 16,000 as a test set. We evaluated the out-of-sample extrapolation by comparing the extrapolated gain in prediction accuracy from 8,000 to 16,000 samples to the ground-truth gain (Figure 1C). Extrapolation and ground-truth pairs were aggregated for each of our prediction tasks. Power-law extrapolations of the learning curve were accurate with an average coefficient of determination of R² = 0.788 (T1 R² = 0.828, rfMRI R² = 0.716, DWI R² = 0.710). The obtained goodness-of-fit statistics and out-of-sample extrapolation suggest that learning curve power laws can be used to estimate trends of maximally achievable accuracy as well as necessary sample sizes for threshold accuracies.

Learning curve extrapolation reveals performance reserves in phenotype prediction

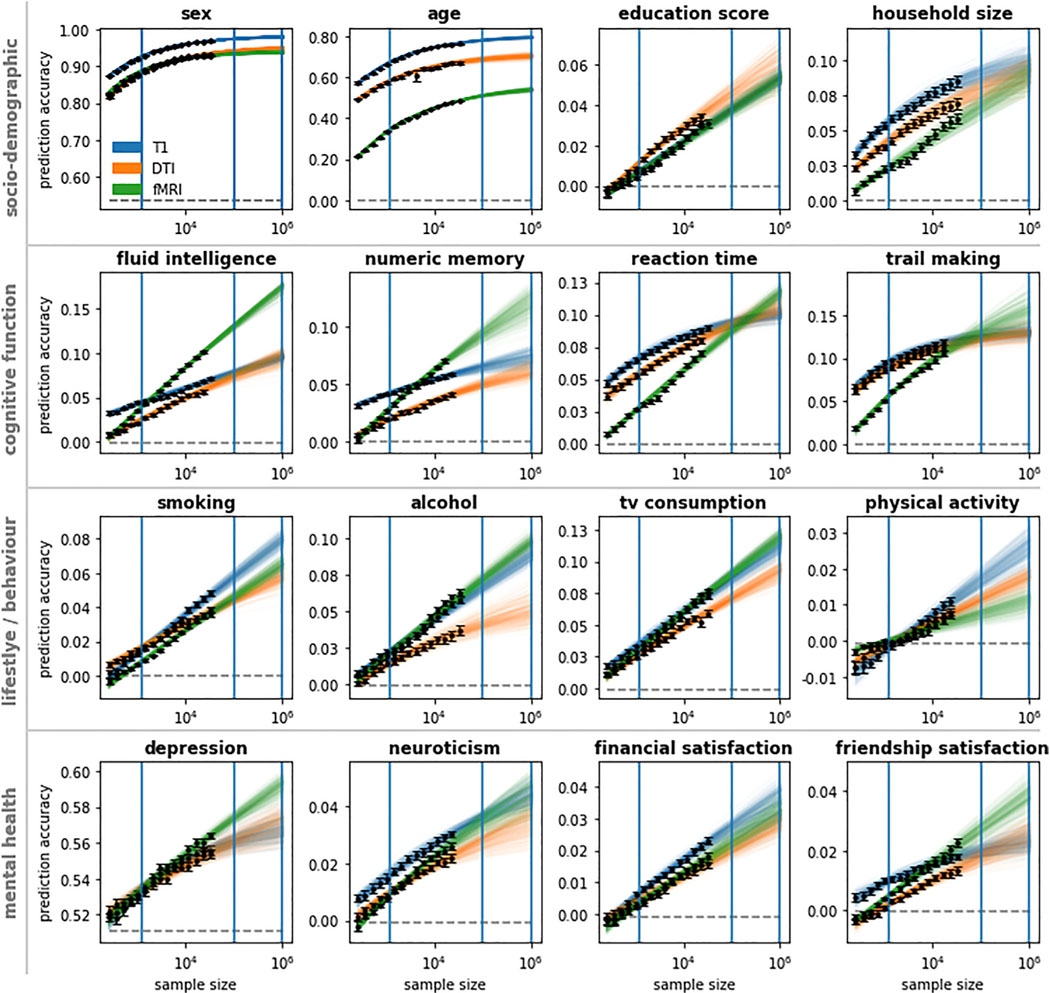
All examined target phenotypes could be predicted from our T1, rfMRI, and DWI brain data, albeit to varying degrees of accuracy. Prediction accuracy (classification accuracy or regression R², respectively) was highest for sex and age (best-performing modality: accuracy/R² at max sample size; sex T1: 0.968 ± 0.001, age T1: 0.762 ± 0.002). Sociodemographic phenotypes (education score DWI: 0.034 ± 0.002, household size T1: 0.085 ± 0.004) and cognitive phenotypes (reaction time T1: 0.090 ± 0.002, numeric memory rfMRI: 0.070 ± 0.002, fluid intelligence rfMRI: 0.101 ± 0.002, trail making T1: 0.120 ± 0.003) scored higher than behavioral phenotypes (alcohol rfMRI: 0.063 ± 0.003, smoking T1: 0.048 ± 0.002, TV consumption rfMRI: 0.077 ± 0.002, physical activity T1: 0.011 ± 0.001) and mental health phenotypes (depression rfMRI: 0.564 ± 0.001, neuroticism T1: 0.030 ± 0.001, financial satisfaction T1: 0.023 ± 0.001, friendship satisfaction rfMRI: 0.023 ± 0.002). However, different target phenotypes yielded wildly heterogeneous learning curves (Figure 2). For sex and age, all three neuroimaging modalities showed saturation of prediction accuracy when increasing the sample size beyond 16,000. In contrast, for every other target phenotype, at least one modality showed stable and continuous improvements in accuracy with increasing sample size (i.e., approximately linear scaling of prediction accuracy with log(n); see Figure 1A.2) up to the 32,000 training samples from the UK Biobank. In these data analysis settings, learning curve extrapolation projected continuous improvements up to at least 1 M samples. These patterns were further supported by our supplementary analyses on other datasets and expanded sets of target phenotypes (Figures S1–S5), even though the specific values varied somewhat in replication datasets on different cohorts or using nonidentical target measures.

Figure 2. Linear models are operating far below ceiling accuracy for most target phenotype predictions.

Learning curves show the collective results obtained from regularized linear models using T1, DWI, and rfMRI data to predict sociodemographic, cognitive function, behavior/lifestyle, and mental health phenotypes. Training datasets were subsampled from the UK Biobank up to a size of 32,000 participants. Learning curves were extrapolated beyond 32,000 participants. To indicate extrapolation uncertainty, each colored line represents a power-law fit based on a bootstrap sample of observed accuracies. Observed prediction accuracies are marked black; majority classifier/median regression baselines are marked dashed gray. Blue vertical lines indicate the sample size of the Human Connectome Project (1,000), the imaging sample size goal of the UK Biobank (100,000), and the proposed Million Brain Initiative (1 M). Error bars indicate SEM.

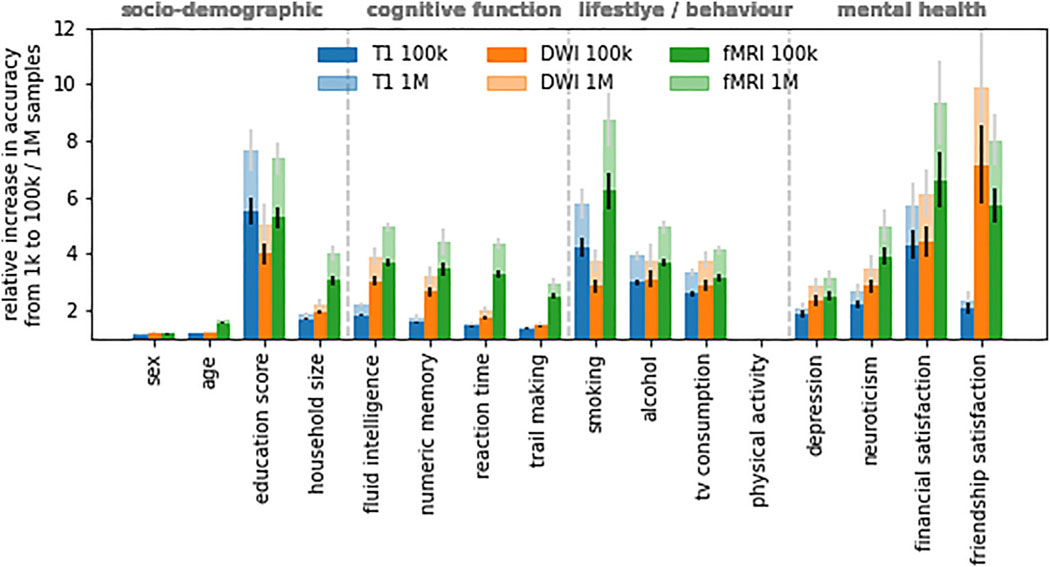
To quantify how prediction performance is projected to gain from further increases in sample size beyond our sample, we used the Human Connectome Project sample size (1,000) as a reference and calculated the expected relative change in accuracy when escalating from 1,000 (Human Connectome Project) to 1 M (Million Brain Project goal) samples (Figure 3). The largest relative change was projected for mental health phenotypes (friendship satisfaction DWI: 8.89 ± 2.14, financial satisfaction rfMRI: 8.34 ± 1.47, depression rfMRI: 2.15 ± 0.27, neuroticism rfMRI: 3.99 ± 0.58) followed by behavioral phenotypes (alcohol rfMRI: 3.94 ± 0.23, smoking rfMRI: 7.74 ± 0.97, TV consumption rfMRI: 3.13 ± 0.18; physical activity could not be reliably estimated due to near-zero baseline), cognitive phenotypes (reaction time rfMRI: 3.35 ± 0.18, numeric memory rfMRI: 3.41 ± 0.47, fluid intelligence rfMRI: 3.92 ± 0.19, trail making rfMRI: 1.92 ± 0.21), and sociodemographic phenotypes (household size rfMRI: 3.04 ± 0.27, education T1: 6.61 ± 0.71). Consistent with observed learning curve saturation, sex (DWI: 0.21 ± 0.01) and age (rfMRI: 0.62 ± 0.03) scored the lowest. In other words, we project a 3- to 9-fold increase in prediction performance for behavioral and mental health phenotypes when moving from 1,000 to 1 M samples. Our results suggest that for most investigated target phenotypes, linear models still operate far below their respective performance ceilings at currently available sample sizes.

Figure 3. Multifold gains in prediction performance are projected for behavioral and mental health phenotypes when moving from 1,000 to 1 M samples.

Shown is the relative increase in prediction accuracy per modality and target phenotype derived from learning curve extrapolation on regularized linear models. Results for physical activity could not be reliably estimated due to near-zero baseline (cf. Figure 2). Error bars indicate SEM.

Optimal choice of imaging modality depends on both target phenotype and sample size

The scaling trajectory of prediction performance with sample size expressed a multitude of patterns based on the specific combination of evaluated brain imaging data and target phenotypes (Figure 2). No single modality consistently outperformed the other modalities, nor did we observe a consistent rank order of modalities over the set of prediction targets. Even for a single target phenotype, different modalities expressed different scaling behavior so that the accuracy hierarchy of modalities would often change with increasing sample size. Nearly every possible rank order of modalities was observed in at least one target phenotype and sample size range. The most frequent rank order was T1 > DWI > rfMRI, representing 40.26% target 3 sample size combinations excluding extrapolated values. However, extrapolated to 1 M samples, rfMRI was projected to outperform T1 and DWI for the majority (9/16) of target phenotypes. A compelling example is the case of fluid intelligence (Figure 2), where T1 outperformed rfMRI by 2.47 percentage points for small sample sizes (n = 256) but was projected to be outperformed by rfMRI by 7.92 percentage points for very large sample sizes (n = 1 M). In some but not all of such cases, T1 and DWI approached saturation accuracy (cf. cognitive function, Figure 2). In contrast, for rfMRI, learning curve extrapolation predicted continuous improvements up to at least 1 M samples (see Figure S7 for a comparison between Human Connectome Project (HCP) and UK Biobank (UKBB) data in terms of sex prediction using functional connectivity features), except for sex and age. In sum, the best-performing modality depended on both target phenotype and sample size, leading to pronounced modality cross-over effects for some target phenotypes. Further, extrapolation of performance scaling with increasing sample size suggests a higher accuracy ceiling for rfMRI than for T1 and DWI.

Multimodal data substantially boost prediction performance

Does combining different imaging modalities yield improvements in out-of-sample prediction performance over a single-modality baseline? Information extracted from different imaging modalities might be independent, so that combining modalities would improve out-of-sample prediction performance, or redundant, so that combining modalities would be ineffective. To investigate the impact of multimodal data, we concatenated the imaging data into dual-modality and triple-modality feature spaces and retained the first 512 principal components for each respective feature space to align feature dimensionalities (cf. Schulz et al.³⁷ and Abrol et al.³⁹). Phenotype prediction based on the combination of T1, DWI, and rfMRI data outperformed prediction based on the respective best single modality for all target phenotypes and led to an average relative increase in accuracy of 30.78% (SD = 18.57 p.p.) at 16,000 samples. Switching from single modalities to multimodal input data led to improvements in prediction accuracy on par with doubling the sample size from 8,000 to 16,000 for 10 out of 16 target phenotypes. Learning curves observed in single-modality experiments (Figure 2) were mirrored in our analysis of multimodal feature spaces (Figures 4 and S8 for an alternative visualization). Our results suggest that different brain imaging modalities do not simply reflect the same limited set of variables but instead offer complementary, nonredundant predictive information for the majority of target phenotypes.

Figure 4. Augmenting single-modality feature spaces to incorporate multimodal input data can lead to improvements in prediction accuracy on par with doubling the sample size.

The 512 leading principal components of single-modality data, or of concatenated dual-modality data, were used as the basis for phenotype prediction. Pictured is the min-max scaled prediction accuracy, with accuracy at 1,000 training samples representing the origin of the respective graph. Switching from single modalities to multimodal input data led to improvements in prediction accuracy for all target phenotypes. For 10 out of 16 target phenotypes, improvements from multimodality were comparable to improvements from doubling the sample size from 8,000 to 16,000. Different brain imaging modalities appear to provide complementary, nonredundant predictive information for most target phenotypes (see Figure S7 for an alternative visualization).

Direct comparison of linear and nonlinear models

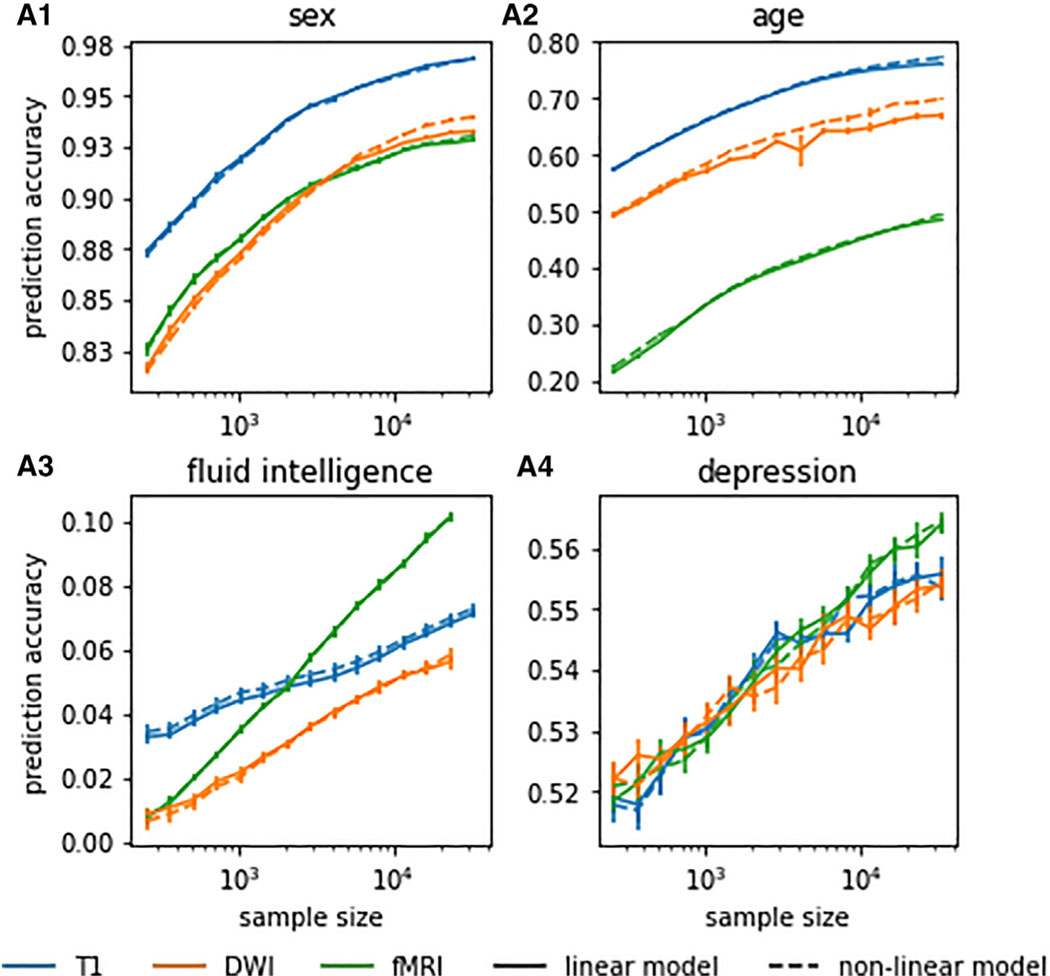
In recent work,³⁷ we observed that linear and more expressive nonlinear machine learning models did not show relevant differences in performance for sex and age prediction based on T1 and rfMRI data for up to 8,000 training samples. We replicated these analyses for age, sex, fluid intelligence, and depression and on up to 32,000 training samples, comparing linear ridge regression with its nonlinear counterpart, RBF-kernelized ridge regression. Only in sex and age predictions based on DWI with large sample sizes above 16,000 did nonlinear models appear to marginally outperform their linear counterparts (Figure 5A.1). On all other evaluated prediction settings, linear models performed on par with nonlinear machine learning models. We found no consistent evidence of exploitable predictive nonlinear structure in neuroimaging data. Our collective results did not qualitatively differ between linear and nonlinear machine learning models.

Figure 5. Linear models performed on par with nonlinear machine learning models in neuroimaging-based phenotype prediction.

We found no consistent evidence of exploitable predictive nonlinear structure in neuroimaging data. Only for DWI-based prediction of sex and age at large (>16,000) training sample sizes did nonlinear models marginally outperform their linear counterparts. Pictured are results for linear and RBF-kernelized nonlinear ridge regression. For other nonlinear machine learning models, see the supplemental information. Error bars indicate SEM.

DISCUSSION

Current research on neuroimaging-based precision medicine suffers from an information gap. Without principled estimates on the mutual information between brain imaging data and a given target phenotype, researchers are limited to a trial-and-error approach in which they are left guessing whether a machine learning model’s bad performance is due to technical error, insufficient sample size, or lack of predictive information in the data. Obtaining principled estimates on the mutual information between brain imaging data and target phenotype should help streamline the development of complex machine learning models, inform large-scale data collection initiatives, and help allocate resources to the most promising phenotypes.

In the present study, we introduced learning curve extrapolation as an effective tool to estimate achievable prediction accuracy and sample size requirements for neuroimaging-based phenotype prediction. Our systematic characterization of learning curves for different imaging modalities and target phenotypes revealed three major findings: first, for most of the investigated target phenotypes, prediction performance continued to improve with additional samples, even at the limit of currently available sample sizes. These untapped performance reserves suggest that machine learning models in neuroimaging-based phenotype prediction operate far below their ceiling accuracy. However, it is important to note that the maximum accuracies were relatively low for all phenotypes except sex and age, which may be a cause for concern regarding the practical utility of these predictions. Second, different imaging modalities yielded unique predictive information, and combining modalities led to improvements in prediction accuracy on par with doubling the sample size. Moving from single imaging modalities to multimodal input data may unlock further substantial performance reserves for neuroimaging-based phenotype prediction. Finally, a majority of target phenotypes exhibited cross-over effects with regard to the best-performing modality. Instead of one single imaging modality being optimal for predicting a given target phenotype, the best-performing modality changed with the sample size. This insight has implications for planning large-scale neuroimaging studies, showing that results from small-scale pilot experiments can be misleading.

Our analyses comprised multiple brain imaging modalities (T1, rfMRI, DWI) and a wide range of sociodemographic, cognitive, behavioral, and mental health target phenotypes, evaluated using both linear and nonlinear machine learning frameworks on one of the largest available brain-imaging datasets. Due to the diversity of imaging modalities and target phenotypes, and owing to sample sizes orders of magnitude beyond the size of traditional neuroimaging studies, we cautiously expect our results to generalize to other neuroimaging-based phenotype prediction scenarios.

Foundational for the present study is the premise that prediction performance follows strict mathematical laws. The gain in prediction accuracy that is enabled by an increase in sample size can be modeled and extrapolated. This allowed us to, in essence, forecast the prediction performance that we would likely reach at sample sizes orders of magnitude larger than the datasets of today. Learning curve extrapolation has already been applied in machine translation,³⁴ genomics,^40,41 and radiology⁴² to assess sample size requirements. Regarding the estimation of learning curves, our investigation makes at least three key contributions. First, we demonstrated consistent and highly accurate (average goodness-of-fit R² = 0.99) power-law scaling of prediction accuracy with sample size in 48 (16 target phenotypes × 3 modalities) common neuroimaging data analysis scenarios. The diversity of analyzed phenotypes and imaging modalities suggests that the power-law functional form can describe learning curves for neuroimaging data, independent of target phenotype or imaging modality. Second, we demonstrated that the underlying power law allows for extrapolating learning curves. While earlier studies^40,42 assumed the integrity of out-of-sample extrapolation without empirical evidence, we experimentally validated our ability to extrapolate learning curves based on subsamples of data. Finally, we conceptually linked the ceiling accuracy of extrapolated learning curves to the amount of predictive information contained in the data. Particularly for research in precision medicine, it is crucial to estimate whether neuroimaging data could ever be predictive of a certain disease or treatment response at a clinically useful accuracy. We argue that the ceiling accuracy of extrapolated learning curves can serve as an estimate of the maximally achievable accuracy and partially answer the question of potential for clinical use. Our present study is, to the best of our knowledge, the first to use the theory of learning curves as an empirical tool to assess the irreducible error, or maximal accuracy, of real-world prediction tasks.

Will structural and functional neuroimaging benefitfrom exceedingly large sample sizes? In machine learning benchmarks datasets of comparable dimensionality like MNIST⁴³ or Fashion,^43,44 linear models approach saturation accuracy at around 1,000 samples.³⁷ One may reasonably expect our neuroimaging data to follow a similar pattern. Indeed, for the prediction of sex and age in all modalities and the prediction of aspects of cognitive function using T1 and DWI, linear models begin to saturate (Figure 3). However, for nearly all other combinations of imaging modality and target phenotype, linear models appear to operate far below their ceiling accuracy. In conjunction with the observation that linear models are competitive with more complex nonlinear models at present sample sizes,^35–37,45 this allows for several conclusions.

Most importantly, there may be more predictive information contained in neuroimaging data than early small-sample trials indicate, although the predicted accuracies remain modest even with large sample sizes. The extent to which quantifiable measures of behavior, cognition, and even mental health can be inferred from structural or functional brain MRI is contentious in the quantitative neuroscience community.^{22,23,46–49} For instance, in the ABCD challenge benchmarking the prediction of fluid intelligence based on T1 data, most contributing researchers reported low (R² < 0.04) explained variance.⁵⁰ While some contributing researchers hypothesized insufficient sample size,⁵¹ others speculated that “structural features alone do not contain enough information related to fluid intelligence to be useful in prediction contexts.”⁵² Our learning curve extrapolation suggests that the amount of explained variance could likely be doubled−or, using rfMRI data, even quadrupled−given enough training samples and that we by far have not exhausted the predictive information in neuroimaging data (Figures 2, 3, 4, and S3–S5). However, it is important to consider how these predictions compare with nonimaging data and their added value for clinical utility, as well as the limitations in generalizing these results to other contexts. Though we cannot draw definitive conclusions on whether structural MRI and fMRI are operating on appropriate temporal or spatial resolutions, our results give cause for cautious optimism that current spatiotemporal resolutions are “good enough.” The majority of medium-sample-regime HCP-sized (~1,000 samples) studies on neuroimaging-based phenotype prediction have likely severely underestimated the accuracy that can be achieved in the limit of larger sample sizes and more robust predictive models.

Contrary to our expectations, rfMRI provided the best prediction accuracy in the limit of large sample sizes of many prediction tasks. fMRI is often criticized for being highly susceptible to a variety of noise sources,^24,25 having low temporal resolution,^53,54 and relying on the BOLD signal as a proxy for neural activity that is far removed from the actual local field potentials.^22,23 Such skepticism is, superficially, supported by comparably low prediction performance at small sample sizes (Figure 2). However, learning curve extrapolation projected that rfMRI would eventually outperform structural imaging modalities in the prediction of the majority (9/16) of target phenotypes (see Figures S6 and S7 for analyses of the impact of rfMRI data quality). Higher-quality rfMRI data, like the longer recordings from the HCP, may further improve results (Figure S7).^55–57 Even with all its shortcomings, rfMRI appears to have a wealth of extractable predictive information. Given that fMRI likely leaves much room for technological innovation,^58,59 we cautiously conclude that fMRI could well allow for single-subject prediction on very large datasets of the future, although the predicted accuracies remain modest even with large sample sizes in this study.

Further, we observed that prediction performance for sex and age is saturating before all other phenotypes. In neuroimaging-based phenotype prediction, there is a well-founded fear that the model may mostly rely on confounding variables like sex and age to derive its prediction. Our results allow for cautious optimism in this regard. Most phenotypes showed continuous improvements in achievable accuracy for the sample size ranges in which accuracies for age and sex confounds are already saturating. Thus, accuracy gains are unlikely to be driven primarily by age and sex confounds and, by the exclusion principle, are more likely to be driven by phenotype-specific effects.

Finally, our results suggest that neuroimaging researchers may need to recalibrate what they consider large sample sizes. Average machine learning studies in the field of precision psychiatry include hundreds up to a few thousand samples⁸; 10,000 is conventionally considered very large. However, 100,000, even 1 M, samples may not be sufficient to characterize simple linear modes for most target phenotypes (Figure 3). This is consistent with sample sizes of widely acknowledged reference datasets from computer vision, for example the popular Imagenet dataset, which comprises 14 M images. As brain images have an even higher dimensionality than photos from Imagenet (cubed instead of squared resolution), excessively large sample sizes may prove necessary to fully extract predictive information in neuroimaging data.

Our collection of findings underlines that “snapshot” measurements of accuracy at a single sample size can be highly misleading when deciding which imaging modality is most promising for predicting a given target phenotype. In particular, cognitive target phenotypes featured cross-over effects, where the most informative imaging modality changed with increasing sample size. Take the example of fluid intelligence (Figure 2): accuracy at a few hundred samples would suggest that T1 yields best performance, contains the most information about the target, and should be prioritized for further research. At a few thousand samples, a researcher may conclude that all modalities work comparably well and that it barely matters which modality to prioritize for further data collection. Only when considering the extrapolated learning curve did it become clear in the present investigation that rfMRI can be expected to substantially outperform structural modalities at high sample sizes for the prediction of fluid intelligence. This cross-over effect is likely driven by different phenotype-specific signal-to-noise ratios of different imaging modalities, leading to heterogeneous sample efficiency and, consequently, differently shaped learning curves.

Modality cross-over effects have implications for the planning and design of large-scale neuroimaging studies. Large-scale studies are often preceded by a pilot experiment to assess sample size requirements and to determine which particular neuroimaging techniques or modalities are most promising for the research question at hand. Without characterizing learning curves, pilot experiments will often produce deceptive results regarding the optimal imaging modality, like erroneously discarding rfMRI in favor of T1 in our example of fluid intelligence, leading to suboptimal design choices down the road. In contrast, learning curve extrapolation from the pilot experiment can reveal not only the optimal imaging modality in the limit of infinite samples but also for specific sample size regimes, facilitating superior design choices regarding sample size and imaging protocol of large-scale neuroimaging studies.

In the present study, mental health phenotypes could be predicted to a lesser accuracy compared to sociodemographic and cognitive phenotypes, alcohol and smoking behavior. This could be due to either particularly high noise in the features that are predictive for mental health compared to other phenotypes or comparatively high noise (i.e., low reliability) in the target variable.

In our results, prediction appeared to work best for objective measures like age, reaction time, and fluid intelligence and worst for less reliable measures derived from subjective experience, like neuroticism or friendship satisfaction. Thus, we hypothesize that noise in the target variable may play an important role in the comparatively low prediction accuracy for mental health phenotypes.

This interpretation of our results ties into current discourse in psychiatry. Many diagnostic categories may insufficiently map on the underlying neurobiology²⁶ or suffer from low inter-rater and low test-retest reliability.^27,28 The concept of unsuitable labels provides a potential way to increase accuracy besides the collection of more and more data: target phenotypes like depression or neuroticism (as used in this study) may be insufficiently reliable due to the subjectivity of individual experience or may insufficiently map on the underlying neurobiology and may need to be redesigned or split into constituent parts to optimize prediction.

The introduction of research domain criteria⁶⁰ targets this problem by searching for “new ways of classifying mental disorders based on dimensions of observable behavior and neurobiological measures.”⁶¹ Such newly derived phenotypes are expected to yield improved reliability and validity. Thus, research domain criteria may not only improve clinical practice but may also benefit neuroimaging-based precision psychiatry by improving the sample efficiency of machine learning models.

In our study, we focus on the more common between-participant settings where models are trained on some participants and used to predict outcomes for others. In these cases, predictive information may be “hidden” behind individual differences in brain structure and function. A within-participants setting could potentially require less training data and yield better results, as the training distribution is closer to the test distribution. This proximity might allow for more apparent statistical relationships between brain and behavior since they are not obscured by significant individual variations. It remains unclear to what extent our results are transferable to the within-participants prediction setting.

Another important consideration is the distinction between predicting past (e.g., education), current (e.g., fluid intelligence at the same visit), and future outcomes (e.g., expected weight gain). Our study focuses on past and current outcomes, but future research should investigate whether brain images differentially contain information for past, current, and future targets.

Furthermore, there may be subtle differences between classification and regression scenarios. Our study primarily focuses on regression targets, as they are comparatively easier to evaluate regarding goodness-of-fit versus multiclass accuracy for highly imbalanced targets with heterogeneous numbers of classes. This approach also allows us to mitigate concerns related to excessive class imbalances. When comparing the results for regression targets in our study with a small minority of classification targets, we observed no significant differences.

Lastly, within any predictive scenario, predicting certain targets on the whole cohort may prove difficult but may be relatively easy on specific subpopulations (e.g., certain disease subtypes, sex differences, socioeconomic groups with different statistical relationships between brain and behavior, and generally cases where the target label merges together conceptually dissimilar aspects, making the target challenging for machine learning models to learn). All four points warrant further investigation in future studies.

Limitations of the study

Our study has multiple conceptual and technical limitations. Conceptually, our learning curves inherently only give a lower bound to practically achievable prediction accuracy for a given model and a given representation of input data. A different model or a different representation of the input data may give different, potentially even better, results. While we cannot fully exclude such possibilities, we are confident in our results on both accounts. For the sample size range analyzed in this study (32,000 and extrapolated up to 1 M), our learning curves may be quite close to the ground-truth achievable accuracy, even for arbitrarily expressive models (cf. Figure 5). We give one empirical and one principled argument for this conjecture. Empirically, a number of recent studies found that linear models performed comparably to their more sophisticated nonlinear counterparts. In prior work,³⁷ we saw virtually no difference in performance when moving from linear models to kernel support vector machines, random forests, gradient boosting, and deep neural networks. Dufumier et al. confirmed this result and concluded that “simple linear models are on par with SOTA [state-of-the-art] CNN [convolutional neural networks] on VBM [voxel-based-morphometry], which suggests that DL [deep learning] models fail to capture nonlinearities in the data.” Though these results are critically discussed by Abrol et al., it does remain controversial how much complex nonlinear models may improve over a well-tuned linear baseline in the analysis of neuroimaging data. High levels of noise in neuroimaging data may effectively linearize decision boundaries, potentially leaving little nonlinear structure for machine learning models to exploit.^37,62 Even if the task of mapping a brain image to a phenotype is nonlinear, we have a principled reason to assume that this nonlinear predictive structure can rarely be exploited at present sample sizes. Our results show that linear models are still operating far below their ceiling accuracy at present sample sizes for nearly all of the analyzed target phenotypes. It follows that the parameters that constitute the linear model cannot be adequately estimated at present sample sizes. The linear model is the simplest possible mapping from features to prediction target, and any nonlinear extension requires additional parameters that would need to be estimated from the same insufficient data. We argue that if there are insufficient data to characterize a linear interaction, then there is little reason to expect to be able to characterize a more complex nonlinear interaction from the same data−unless the model implements an inductive bias specifically suited to the precise type of nonlinear interaction in the data, e.g., by incorporating neuroscientific domain knowledge.

Regarding a better representation of features, we are using the state-of-the-art representation of neuroimaging data, derived from years of experience and incorporating vast neuroscientific domain knowledge from nonlinear registration to feature creation based on cortical or volumetric parcellation. For a machine learning model like, for example, a deep neural network operating on minimally preprocessed T1 images to learn an internal representation that outcompetes the carefully handcrafted representations we have available today is a substantive challenge, and positive results^39,63–65 are still controversially debated.^36,37,66

Further, it should be reiterated that archivable prediction accuracy and its precise scaling behavior can depend on the given cohort and the type and reliability of the specific measures used to assess the target phenotype. Effects of such cohort and target phenotype differences are illustrated in the supplemental information (Figures S1 and S2).

Technical limitations pertain to the representation of target variables and to uncertainty quantification. It is difficult to make direct comparisons of prediction accuracy between different target phenotypes due to heterogeneous coding of the target variables. Moreover, our analysis was constrained by the small number of positive cases for psychiatric and neurological diseases in the UKBB, limiting us at times to less common prediction targets for which information was available for nearly all participants. The explained variance (R²), which we report as a metric of prediction performance, has no intrinsic meaning and can only be interpreted in reference to the given coding, retest reliability, and construct validity of a given target variable.

Finally, the quantification of uncertainties on the results of cross-validation schemes is an area of active research and has no established solutions. Our Monte Carlo cross-validation approach should yield legitimate estimates of uncertainty for small sample sizes, for which subsampled sets will be approximately statistically independent. When we approach 32,000 training samples, sampled from a finite base population, statistical independence is violated, and error bars in all figures should be taken with caution. Consequently, we intentionally restrict ourselves to mostly qualitative interpretation of results and refrain from explicit statistical inference on the level of learning curves and from reporting explicit confidence intervals on the results of learning curve extrapolations.

In conclusion, we argue that the amount of predictive information contained in neuroimaging data, particularly in rfMRI, is likely underestimated, combined with, and partly due to, an overoptimistic assessment of the sample efficiency of machine learning models on neuroimaging data. However, the often still quite low extrapolated accuracies raise doubts about the practical usefulness of neuroimaging-based phenotype prediction. We recommend characterizing and extrapolating learning curves as an essential part of pilot experiments to test feasibility by estimating the achievable accuracy, assess sample size requirements, and establish the optimal imaging modality regardless of cross-over effects.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Marc-Andre Schulz (marc-andre.schulz@charite.de).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• This paper analyzes existing, publicly available data. Neuroimaging data was obtained from UK Biobank under Data Access Application 33073 and are available on request directly from the UK Biobank (http://www.ukbiobank.ac.uk/register-apply/).

• Code for learning curve estimation is available here https://github.com/brain-tools/esce; DOI: https://doi.org/10.5281/zenodo.10019019.

• Any additional information required to reanalyze the data reported in this work paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS

Dataset and feature spaces

Our analyses required large sample sizes to reliably estimate learning curves. Hence, we based our analyses on the UK Biobank,⁶⁷ which has been described as the “world’s largest multi-modal imaging study”.¹² The UK Biobank provides genotyping as well as extensive phenotyping data on approximately half a million participants, out of which 46197 (June 2021 release) underwent additional medical imaging. Structural T1-weighted brain images, resting-state fMRI, and diffusion-weighted brain images are available for each of these participants. For details on the UK Biobank’s data acquisition and processing protocols, please refer to Alfaro-Almagro et al.

A majority of past and present studies on machine learning for clinical neuroimaging rely on features designed by domain experts; cf. recent reviews on machine learning in epilepsy,⁶⁸ autism,⁶⁹ stroke,⁷⁰ and mild cognitive impairment.⁷¹ The UK Biobank directly provides widely used feature representations (IDPs) for structural, functional, and diffusion tensor imaging. To align with common usage of neuroimaging feature representations and to increase reproducibility, we used the UK Biobank-provided features for our analysis. The structural MRI features (1425 descriptors) represented regional gray and white matter volumes, and parcellated cortical thickness and surface area.⁷² Resting-state functional MRI was distilled into a functional connectivity matrix (1485 descriptors), based on networks derived from a 100-component group ICA,⁷² note that the UK Biobank only records a comparatively short 5 min of rfMRI - for a direct comparison to the 30 min Human Connectome Project rfMRI data, see Figure S6). Diffusion-weighted imaging features (675 descriptors) represented fractional anisotropy, mean diffusivity and tensor mode, intra-cellular volume fraction, isotropic or free water volume fraction and orientation dispersion index for “over 75 different white-matter tract regions based both on subject-specific tractography and from population-average white matter masks”.¹³ For details on the UK Biobank’s pre-computed feature representations, please refer to Alfaro-Almagro et al. Aside from standard scaling, features were used exactly as provided by the UK Biobank.

Prediction targets and target variable coding

Widely studied sociodemographic, cognitive, behavioral, and mental health phenotypes served as prediction targets for our analyses. Specifically, we included participant age (UK Biobank field-ID 21003–2), sex (field 31–0), education score (field 26414–0), and household size (number of people in household, field 709–2) as sociodemographic phenotypes. Fluid intelligence (summary score, field 20016–2), reaction time (mean time to correctly identify matches, field 20023–2), numeric memory (maximum digits remembered correctly, field 4282–2), trail making (interval between previous point and current one in alphanumeric path, field 6773–2) represented cognitive phenotypes. Alcohol consumption (intake frequency, field 1558–2), tobacco consumption (intake frequency, field 1249–2), physical activity (International Physical Activity Questionnaire activity group, 22032–0), TV consumption (hours per day, field 1070–2) represented behavioral and lifestyle phenotypes. Finally, depression (ever felt depressed for a whole week, field 4598–2), neuroticism (summary score, field 20127–2), friendship satisfaction (field 4570–2), and financial satisfaction (field 4581–2) represent mental health. For detailed information on the prediction targets, please refer to the UK Biobank online documentation (https://biobank.ndph.ox.ac.uk/showcase).

With the exception of sex and depression, all targets are either continuous or ordinally represented and were treated in a regression setting. Prediction of sex and depression, both binary targets, was treated as a classification task. All target phenotypes were provided by UK Biobank and used as-is, excluding “prefer not to answer” and “do not know” responses on a per-phenotype basis. Full phenotype information was not available for all participants, so that we generally report results for 16 thousand participants or the maximum available sample size per target phenotype (see Table S1).

METHOD DETAILS

Machine learning models and out-of-sample validation

For each combination of MRI modality, target phenotype, and training sample size, we subsampled the data into a training set (n = 256, 362, 512,…, 32k), a validation set for hyperparameter tuning (n = 2k), and a test set for final evaluation of prediction accuracy (n = 2k). The subsampling into train, validation, and test sets was repeated 20 times (Monte Carlo cross-validation, also known as repeated random sub-sampling validation) to provide an averaged accuracy as well as uncertainty estimates. Uncertainties were derived by bootstrapping over the cross-validation resamplings. Samples of train, validation, and test sets can be considered approximately independent for small train set sizes. For large train set sizes, train sets will overlap, and uncertainty estimates must be viewed with caution.

A new machine learning model was trained on the train set, tuned on the validation set, and the best hyperparameter configuration evaluated on the test set, for each MRI modality (n = 3), target phenotype (n = 16), training sample size (n = 15), and cross-validation resampling (n = 20). We used ridge regression (l2 regularized linear regression, sklearn.linear_model. Ridge, Pedregosa et al. for regression tasks, and logistic regression (l2 regularized, sklearn.linear_model.LogisticRegression,⁷³ for classification tasks. Regularized linear models are considered highly competitive in the analysis of neuroimaging data and performed on par with more complex nonlinear models, such as kernel support vector machines and deep artificial neural networks, on similar prediction tasks.^35–37

Hyperparameter tuning on the validation set was performed separately for each fitted model. For ridge regression, alpha values from 2^{^}−15 to 2^{^}15 were evaluated in steps of 2^{^}-(2n+1). For logistic regression, l2 penalty weights ranged from 2^{^}−20 to 2^{^}10 in insteps of 2^{^}-(2n). Hyperparameter ranges and granularity of the search range were checked visually for each modality x target phenotype combination.

Learning curve fitting

The empirical scaling of prediction performance with increasing training sample size is called a learning curve. Theoretical results from statistical learning theory state that learning curve bounds follow a power law function.^29–32 Empirically, power law scaling was shown for models ranging from linear estimators to deep neural networks.^33,34 Thus, we fitted the expected power law functional form [αn^−β + γ] to our empirical data. Learning curves were averaged over the 20 cross-validation resamplings before fitting the power law via nonlinear least squares (scipy.optimize.curve_fit).⁷⁴ Parameters were bound to 0<α<inf, -inf<β < 0, and 0<γ < 1.

QUANTIFICATION AND STATISTICAL ANALYSIS

For learning curve estimation and extrapolation we used the ESCE software (see Data and code availability). Uncertainty estimates are derived via bootstrapping over the cross-validation resamplings. Statistical details are included in the figure legends, further implementation details are available in the ESCE documentation and code.

We intentionally restrict ourselves to mostly qualitative interpretation of results and refrain from explicit statistical inference on the level of learning curves, and from reporting explicit confidence intervals on the results of learning curve extrapolations (see discussion).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
UK Biobank core and imaging data	www.ukbiobank.ac.uk	N/A
Software and algorithms
ESCE	https://github.com/brain-tools/esce	https://doi.org/10.5281/zenodo.10019019

Highlights.

• Full predictive information in brain images not utilized even at 1 M samples

• Multiple imaging modalities improve accuracy akin to doubling sample size

• Most informative modality varies with larger sample sizes

• Achieving practical utility may require prohibitively large samples