Figure 1. Relative free energy calculations predict the impact of single point mutations using thermodynamic cycles that each involve transformations in two environments.

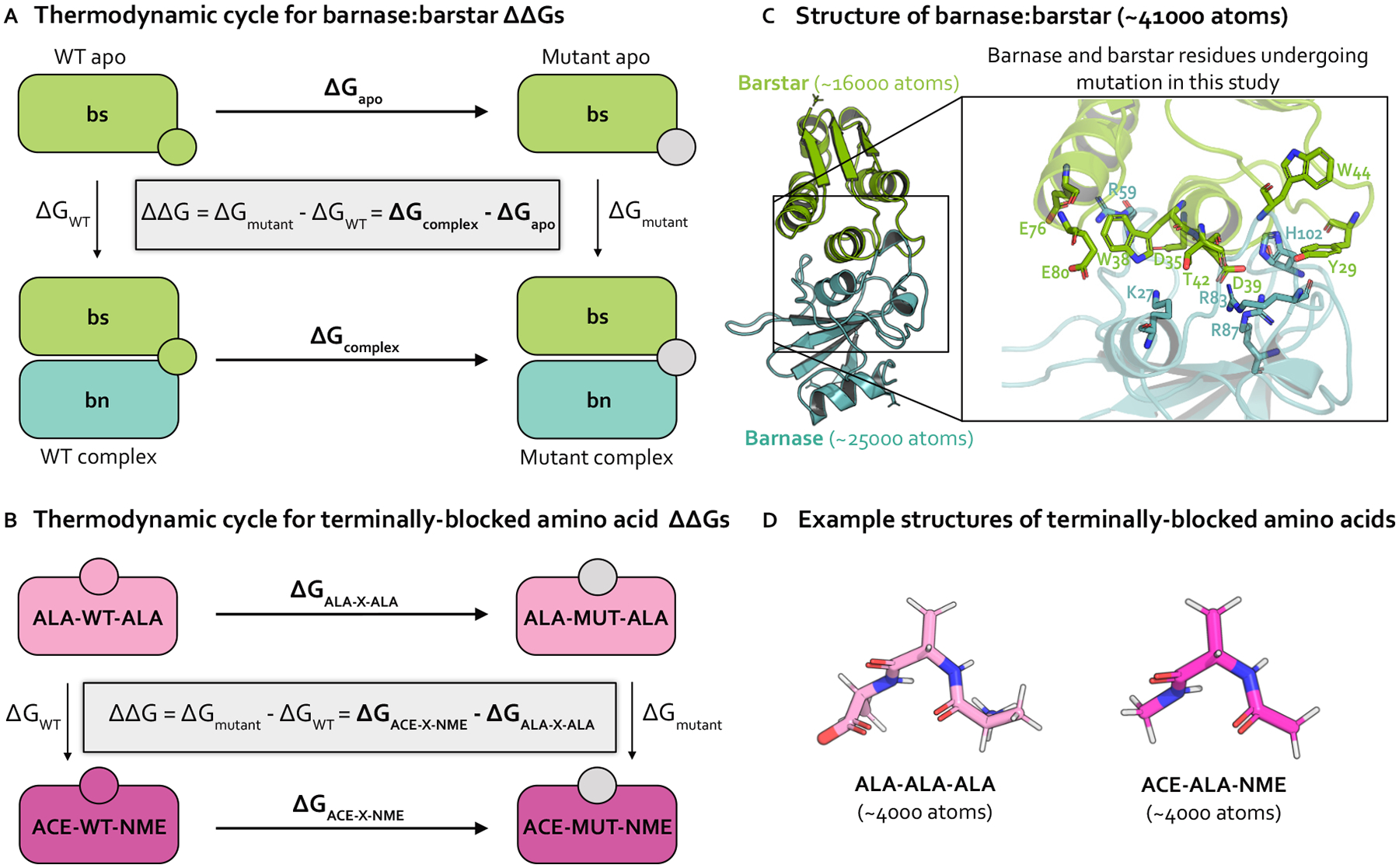
(A) Thermodynamic cycle representing how the relative binding free energy (ΔΔG_binding) can be computed for a protein mutation in the barnase:barstar complex. By cycle closure, the ΔΔG equation shown inside the thermodynamic cycle can be recovered. In practice, it is easier to compute the horizontal legs (ΔG_apo and ΔG_complex, shown in bold) [33], which involve transforming a WT residue (green circle) into a mutant residue (gray circle). The free energy differences for each phase (apo and complex) are subtracted to compute the ΔΔG_binding (B) Thermodynamic cycle representing how the relative free energy (ΔΔG) can be computed for a protein mutation between two phases of terminally-blocked amino acids. The horizontal legs (ΔG_ALA-X-ALA and ΔG_ACE-X-NME), shown in bold) are simulated, which involve transforming a WT residue (magenta or pink circle) into a mutant residue (gray circle). The free energy differences for each phase (ACE-X-NME and ALA-X-ALA) are subtracted to compute the ΔΔG. (C) Structural model of barnase:barstar (PDB ID: 1BRS) with barstar shown in green and barnase shown in blue. Barstar and barnase contain ~ 16000 and ~ 25000 atoms, respectively (including hydrogens and solvent). Zoomed-in view of the barnase:barstar interface shows the 13 residues undergoing mutation in this study (all of which are interfacial) as sticks. Nitrogen atoms shown in blue and oxygen atoms are shown in red. (D) Example structural models of terminally-blocked amino acids: ALA-X-ALA and ACE-X-NME (where X is ALA) shown in pink and magenta, respectively. Each terminally-blocked amino acid contains ~ 4000 atoms (including hydrogens and solvent). Nitrogen atoms are depicted in blue, oxygen atoms in red, and hydrogen atoms in white.