Figure 3. The relative free energy difference (ΔΔG) predictions for small terminally-blocked amino acid mutations are internally consistent and show good convergence, but several of the predictions for interfacial barnase:barstar mutations show poor internal consistency due to slow convergence of complex phase free energy differences (ΔG_complexS).

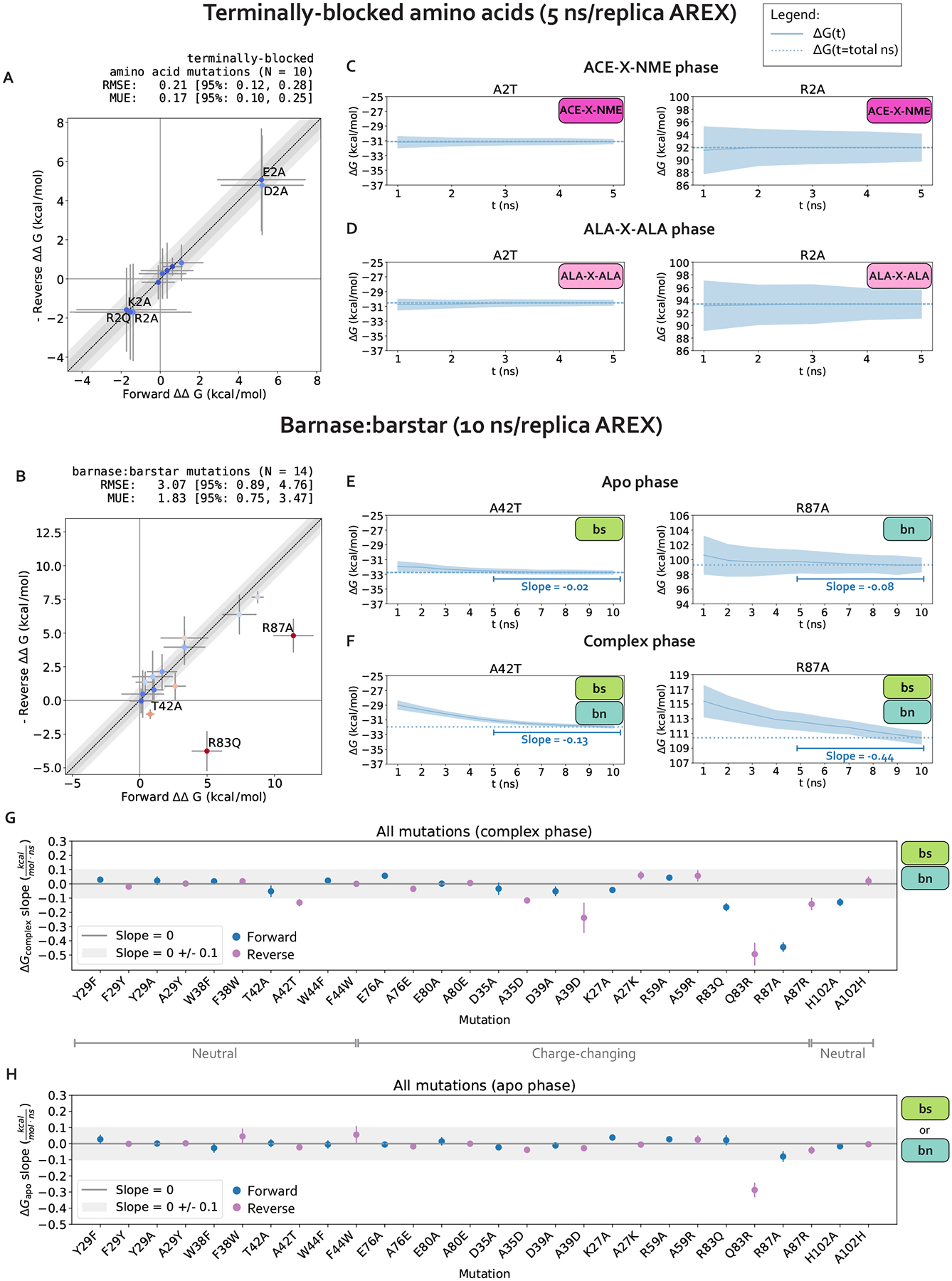
(A) (Negative of the) Reverse versus forward ΔΔGs for each terminally-blocked amino acid mutation computed using alchemical replica exchange (AREX) simulations (number of states = 12 and 24 for neutral and charge mutations, respectively, and simulation time =5 ns/replica for each phase). Data points are labeled if the mutation involves a charge-change (to emphasize that our counterion introduction scheme works well in the absence of sampling problems). The y = x (black dotted) line represents zero discrepancy between forward and (negative of the) reverse ΔΔGs, the dark gray shaded region represents 0.5 kcal/mol discrepancy, and the light gray region represents 1 kcal/mol discrepancy. Data points are colored by how far they are from zero discrepancy (dark blue and red indicate close to and far from zero, respectively). Error bars represent two standard deviations and were computed by bootstrapping the decorrelated reduced potential matrices 200 times. Root mean square error (RMSE) and mean unsigned error (MUE) are shown with 95% confidence intervals obtained from bootstrapping the ΔΔGs 1000 times. (B) (Negative of the) Reverse versus forward ΔΔGs for each barnase:barstar mutation computed using alchemical replica exchange (AREX) simulations (number of states = 24 and 36 for neutral and charge mutations, respectively and simulation time = 10 ns/replica for each phase). Data points are labeled if the forward and (negative of the) reverse ΔΔG_bindings are not within statistical error of each other (i.e., neither the forward nor the negative reverse ΔΔG_binding is within 1 kcal/mol of the 95% Cl for the other ΔΔG_binding). For more details on the plot and error bars, refer to the caption for panel A. (C) Free energy difference (ΔG) time series for representative mutations A2T (left) and R2A (right) in the ACE-X-NME phase. Alchemical replica exchange simulations were performed with number of states = 12 and 24 for A2T and R2A, respectively and the simulation time was 5 ns/replica. Dashed line indicates the ΔG at t = 5 ns. Shaded region represents ± two standard deviations, which were computed by bootstrapping the decorrelated reduced potential matrices 200 times. (D) Same as (B), but for the ALA-X-ALA phase, instead of the ACE-X-NME phase. (E) Free energy difference (ΔG) time series for the apo phase of representative mutations with sampling problems: A42T (left) and R87A (right). Alchemical replica exchange simulations were performed with number of states = 24 and 36 for A42T and R87A, respectively and the simulation time was 10 ns/replica. Dashed line indicates the ΔG at t = 10 ns. For details on the error bars, refer to the caption for panel C. (F) Same as (E), but for the complex phase instead of the apo phase. (G) Slopes of the last 5 ns of the ΔG_complex time series for each barnase:barstar mutation are shown as blue (forward mutations) and purple (reverse mutations) circles. ΔG_complex time series were generated from complex phase AREX simulations (number of states = 24 and 36 for neutral and charge mutations, respectively, and simulation time = 10 ns/replica). Error bars represent 2 standard deviations and were computed using the SciPy linregress function. Slopes within error of the shaded gray region (0 ± 0.1 kcal/mol/ns) are close to zero and are therefore considered “flat.” (H) Same as (G), but for apo phase barnase or barstar mutations instead of complex phase barnase:barstar mutations.