Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2024 Jun 19;631(8019):118–124. doi: 10.1038/s41586-024-07507-9

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2024

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

PMC Copyright notice

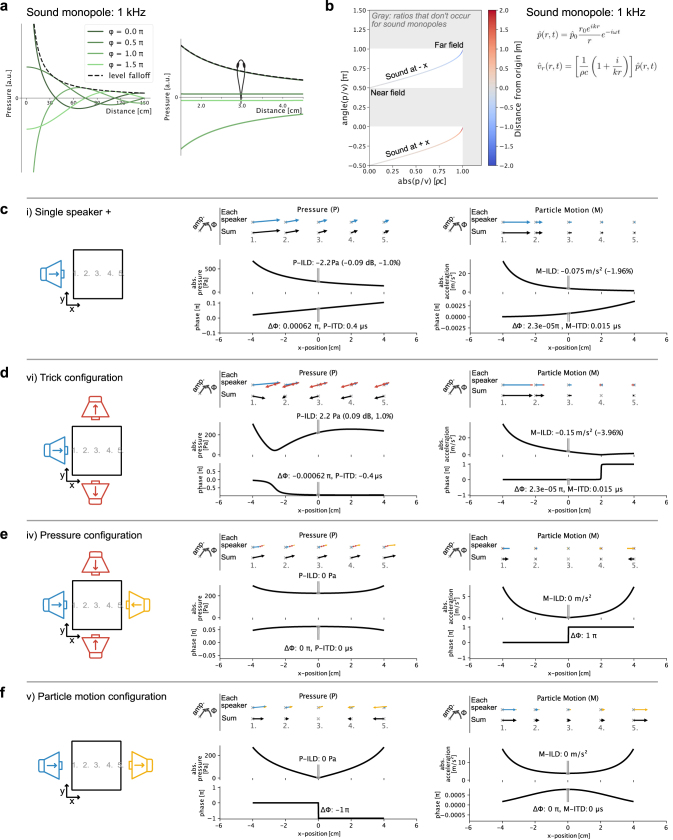
Extended Data Fig. 8 — a, Pressure level (dashed line) falloff next to a sound monopole at several phase snapshots of a propagating wave. Left: Falloff of a 1 kHz wave over 1.5 m. Right: The falloff across the width of the fish at 3 cm distance to a monopole sound source stems from the level falloff with distance. b, Both amplitude ratio and relative phase between pressure and particle velocity change in a distance-dependent manner. Both sound directions (-x, x) stay separate in the relative phase between pressure and particle velocity. c-f, Results of a simple model used to illustrate level and phase of pressure and motion along the horizontal x-axis of the inner tank. The idealized speaker activations in the different sound configurations are modeled as sinusoidal monopole sound sources (see pressure equation in b) located 6 cm away from the origin with frequency f = 780 Hz and speed of sound c = 1500 m/s. Acceleration is calculated from the spatial pressure gradient along the x-axis. The top rows are phasor representations of pressure or motion at five positions along the horizontal axis as indicated in the left cartoon. ILDs and ITDs are computed across a distance of 600 µm centered at the origin. See also Fig. 4 for a summary on ILD and ITD across sound configurations. c, In the single speaker configuration, P-ILD, P-ITD, M-ILD, and M-ITD could be interpreted as rightward cues by the fish. M-ITD is even smaller than P-ITD as motion phase propagates slower than pressure phase in the near field. d, In the trick configuration, P-ILD and P-ITD are inverted, while M-ILD and M-ITD remain unchanged as compared to the single speaker configuration. c-d, See Methods section on interaural cues for comparable P-ILD and M-ILD measurements in our setup. Note that we model monopoles in open water here, but the actual speakers are extended pressure sources in a tank. e-f, In both the pressure configuration and the particle motion configuration P-ILD, P-ITD, M-ILD, and M-ITD are zero or undefined.