Covariate-guided Bayesian mixture of spline experts for the analysis of multivariate high-density longitudinal data

Summary

With rapid development of techniques to measure brain activity and structure, statistical methods for analyzing modern brain-imaging data play an important role in the advancement of science. Imaging data that measure brain function are usually multivariate high-density longitudinal data and are heterogeneous across both imaging sources and subjects, which lead to various statistical and computational challenges. In this article, we propose a group-based method to cluster a collection of multivariate high-density longitudinal data via a Bayesian mixture of smoothing splines. Our method assumes each multivariate high-density longitudinal trajectory is a mixture of multiple components with different mixing weights. Time-independent covariates are assumed to be associated with the mixture components and are incorporated via logistic weights of a mixture-of-experts model. We formulate this approach under a fully Bayesian framework using Gibbs sampling where the number of components is selected based on a deviance information criterion. The proposed method is compared to existing methods via simulation studies and is applied to a study on functional near-infrared spectroscopy, which aims to understand infant emotional reactivity and recovery from stress. The results reveal distinct patterns of brain activity, as well as associations between these patterns and selected covariates.

1 Introduction

Time series are realizations of random processes. Obtaining estimated trajectories may provide insights into many practical problems. Functional near-infrared spectroscopy (fNIRS) is a noninvasive brain imaging technique that measures changes in both oxy- and deoxy-hemoglobin using near-infrared light (Jobsis, 1977). In fNIRS, processed data are nonstationary multivariate time series with a nonconstant mean and high variability across time, which pose many statistical challenges in inference and estimation. Different subjects could have distinct patterns of multivariate longitudinal trajectories, which could be associated with certain clinical or demographic characteristics. The analysis of fNIRS data requires an appropriate method for the analysis of a collection of multivariate high-density longitudinal data observed from different subjects.

Cluster analysis is often used to address the issue of heterogeneity and identify subgroups from collections of time series observed from different subjects. Time series clustering has been used in diverse scientific areas to discover trajectory patterns, which can uncover valuable information from complex and massive datasets (Liao, 2005). Time series and high-density longitudinal clustering partitions the entire collection of data into different groups such that homogeneous time series are grouped together based on a certain similarity measure. Several authors have proposed clustering algorithms for multivariate time series. Kakizawa et al. (1998) used Kullback–Leibler discrimination information as the minimum discrimination criterion for clustering multivariate Gaussian time series. Wang et al. (2007) used a modified K-means clustering algorithm for clustering multivariate time series based on univariate structures. Euan et al. (2019) proposed a coherence-based time series clustering that is able to include both within and between-cluster dependence. A variety of papers have established different model-based clustering methods for clustering multivariate time series, such as multivariate autoregressive models (He et al., 2022), a hidden Markov model (Li et al., 2001), and smoothing splines (Krafty et al., 2017). A comprehensive review of methods for time series clustering can be found in Liao (2005) and in Maharaj et al. (2019).

Covariate-dependent structures can often be associated with the mixture components from a clustering of time series. Bertolacci et al. (2022) presented an analysis of multiple nonstationary time series by using a covariate-dependent infinite mixture with logistic stick-breaking weights, where mixing weights are computed based on covariates. The mixture-of-experts model (Jacobs et al., 1991) assigns weights to each expert via covariate-dependent multinomial logits. Huerta et al. (2003) addressed the issue of time series model mixing based on covariates using the hierarchical mixture-of-experts (Jordan and Jacobs, 1994).

Smoothing splines, which are nonparametric methods that utilize roughness-based penalties, have been widely used in the analysis of time series and longitudinal trajectories (Wang, 2011; Gu, 2013). Bayesian interpretations of smoothing splines were first discussed by Kimeldorf and Wahba (1970). Wahba (1978) showed that the solution to the smoothing splines objective function is equivalent to Bayesian estimation with a partially diffuse prior. Speckman and Sun (2003) adopted a fully Bayesian approach for implementing smoothing splines with a noninformative prior on the variance component, as well as derived necessary and sufficient conditions for the propriety of the posterior. Smoothing splines require estimation of a large number of coefficients, which might be impractical in high-dimensional settings. Gu and Kim (2002) used a subset of reproducing kernel functions to achieve a low-dimensional approximation. Wood et al. (2002) obtained a subset of basis functions using the eigen-decomposition of the Gaussian kernel. Krafty et al. (2017) proposed a tensor-product model for the analysis of replicated multivariate time series which decomposes the power spectrum into products of univariate outcomes and frequencies.

Our goal in this article is to propose a multivariate longitudinal modeling strategy for fNIRS data and to perform covariate-guided clustering of multivariate high-density longitudinal data that can capture trajectory patterns of mixture components, as well as evaluate the relationship between covariates and trajectory patterns. To this end, each mixture component is modeled via smoothing splines, and time-independent covariates are incorporated into the mixture model via the mixing weights. The method is formulated in a fully Bayesian framework. The rest of this article is organized as follows. In Section 2, we introduce the motivating study. Sections 3 and 4 present the proposed model and priors. Section 5 introduces the sampling scheme. In Section 6, we report simulation results under different settings, and Section 7 illustrates our proposed method with application to the motivating study. Section 8 concludes the paper with a discussion.

2 Motivating study

Our motivating study aims to understand patterns of infants’ brain activity before, during and after an emotionally stressful probe called face-to-face still-face (FFSF) (Tronick et al., 1978). Participant mothers in this study were recruited from the longitudinal Pittsburgh Girls Study (PGS), a population-based study of 2,450 girls who were recruited in the city of Pittsburgh between the ages of 5 and 8 (Keenan et al., 2010). In 2016, a large-scale sub-study of the PGS was initiated to investigate how environmental factors, such as psychological stressors experienced during childhood and adolescence, affect later maternal pregnancy and child health. The study is part of the National Institutes of Health Environmental Influences of Child Health Outcomes (ECHO) program, which examines different impacts of prenatal environmental exposures across biological, chemical, physical, and social domains on offspring health and development (Gillman and Blaisdell, 2018). The PGS-ECHO study enrolls PGS participants as they become pregnant or recently deliver a live birth. Participants complete multiple prenatal lab visits and the children are followed from ages 6 to 36 months. The lab protocol includes interviews and interaction tasks to assess contextual stressors, health, mood, lifestyle behaviors, and offspring behavioral and emotional development.

Face-to-face interactions between mothers and infants are essential to the development of infants with respect to communication and social skills, as well as the regulation of emotion and temperament (Hipwell et al., 2019). The FFSF paradigm is a widely used stress task (a violation of the expectation of social interaction) that allows for biobehavioral measurement of individual differences in infant response and recovery. The FFSF comprises of three phases: interact (or baseline), still-face, and recovery (Adamson and Frick, 2003). In phase 1, mothers perform normal interactions with infants without the use of toys; this phase serves as the baseline. In phase 2, mothers adopt a neutral facial expression (still-face with no facial or oral communication) to infants, followed by phase 3, where mothers resume normal interactions with their infants. Prior to the start of the FFSF, an fNIRS cap is fitted on the infant’s head to measure the level of and change in brain activation across the three phases.

PGS-ECHO fNIRS still-face data are recorded using a continuous NIRS imaging system (NIRScout; NIRx Medical Technologies, Berlin, Germany) at the sampling rate of 7.8125 Hz and using the NIRStart acquisition software. The data are measured simultaneously at two wavelengths (760 nm and 850 nm). This fNIRS probe consists of 12 channels from 8 sources and 4 detectors, and a figure of the fNIRS probe configuration is given in the Supplementry material.

In the current study, we measured infant brain activity using the above fNIRS probe (roughly 120 s of measurements for each phase). At the end of 2021, recorded fNIRS still-face data had been collected from 155 infant subjects. Demographic variables along with parent reports on the Infant Behavior Questionnaire-Revised (IBQ-R) (Gartstein and Rothbart, 2003) were also collected. By removing infants who did not complete the three phases of the still-face paradigm, who had large outliers based on leverage, and who had a very short period of measurements in any of the three still-face phases, there were a total of 82 subjects with complete fNIRS still-face data available for future analysis. Data preprocessing steps were performed including data interpolation and rescaling. Finally, processed fNIRS data had a total of 1,500 measurement points for each subject and each channel, where each phase consisted of 500 points. All measurements and sampling times were rescaled to be between 0 and 1, with the interact phase occurring between time 0 and 1/3, still-face between 1/3 and 2/3, and recovery between 2/3 and 1.

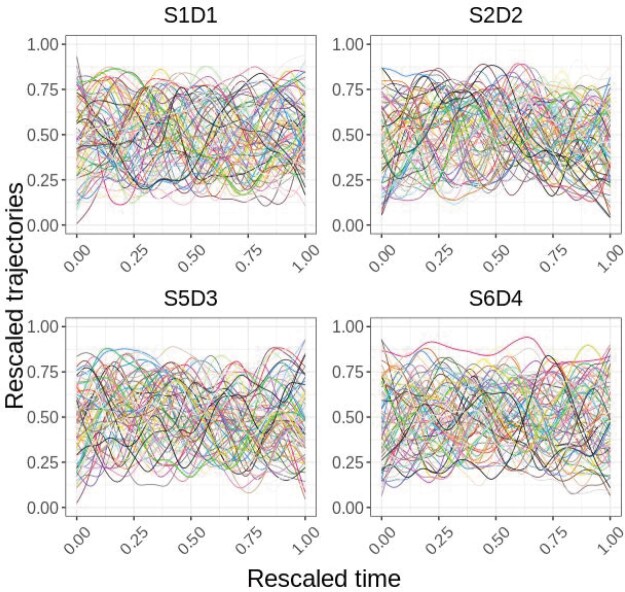
Figure 1 displays trajectories of four selected channels in the prefrontal cortex for each subject. Multivariate longitudinal trajectories are referred to as fNIRS trajectories across multiple channels. Different trajectory patterns are observed for each subject and each channel, which demonstrates heterogeneity and the need for multivariate trajectory clustering as a function of related variables of interest. The goals of our analysis are to identify distinct patterns of brain activity trajectories from multiple fNIRS channels represented by the relative concentration of oxy-hemoglobin, and to assess the association between brain activity trajectories and relevant covariates. In particular, our main scientific question is in understanding associations between the subjective, parent-reported measures of child temperament in the IBQ that is commonly used in clinical settings, and objective measures of neurological activity during a controlled laboratory task.

Fig. 1.

Processed fNIRS trajectories of four selected channels for each subject.

3 Model

In this section, we provide a detailed description of our proposed covariate-guided Bayesian mixture of spline experts model. The proposed model consists of spline components whose mixing weights depend on covariates.

3.1 Mixture of splines model

We propose a tensor-product mixture of splines model for multivariate high-density longitudinal data. For each subject $i=1,\dots ,N$, let ${\mathit{y}}_i={({\mathit{y}}_{i1}^{\prime },\dots ,{\mathit{y}}_{ik}^{\prime },\dots ,{\mathit{y}}_{iK}^{\prime })}^{\prime }$ be the nK-vector corresponding to the K-dimensional trajectories for $k=1,\dots ,K$, where ${\mathit{y}}_{ik}={[y_{ik}(t_1),\dots ,y_{ik}(t_j),\dots ,y_{ik}(t_n)]}^{\prime }$ contains the trajectory of measurements on the kth entry of the data evaluated over a grid of n time points for $j=1,\dots ,n$, and ${\mathit{ϵ}}_i={({\mathit{ϵ}}_{i1}^{\prime },\dots ,{\mathit{ϵ}}_{iK}^{\prime })}^{\prime }$ is the nK-vector of errors. Following the model representation of Krafty et al. (2017), the tensor-product model for the K-dimensional multivariate trajectories, conditional on component g, $g=1,\dots ,G$, can be written as:

$$\left\{{\mathit{y}}_i\right|z_{ig}=1\}=({\mathit{I}}_K\otimes \mathit{X}){\mathit{\alpha }}_g+({\mathit{I}}_K\otimes \mathit{W}){\mathit{\beta }}_g+{\mathit{ϵ}}_i,$$ (3.1)

where ${\left\{z_{ig}\right\}}_{g=1}^G$ are latent indicators as described in Section 3.3, ${\mathit{\alpha }}_g={({\mathit{\alpha }}_{g1}^{\prime },\dots ,{\mathit{\alpha }}_{gK}^{\prime })}^{\prime }$ is a 2K-vector of intercepts and slopes, ${\mathit{\beta }}_g={({\mathit{\beta }}_{g1}^{\prime },\dots ,{\mathit{\beta }}_{gK}^{\prime })}^{\prime }$ is a mK-vector of basis function coefficients as described in Section 4.1, ${\mathit{I}}_K$ is a K × K identity matrix and ⊗ denotes a tensor product. The matrix X is given by $\mathit{X}={\left(\begin{array}{cccc}1& 1& \dots & 1\\ t_1& t_2& \dots & t_n\end{array}\right)}^{\prime }$ and the m columns of the matrix W are smoothing splines basis functions as described in Section 4.1. We assume the error vector ${\mathit{ϵ}}_i$ follows a $\text{MVN}(0,{\mathbf{\Psi }}_g\otimes \mathit{U})$ distribution, where $\mathit{U}={\mathit{I}}_n$ is the n × n identity matrix, and ${\mathbf{\Psi }}_g=\text{diag}({\mathit{\sigma }}_g^2)$ is a K × K diagonal matrix with the error variances ${\mathit{\sigma }}_g^2={({\sigma }_{g1}^2,\dots ,{\sigma }_{gK}^2)}^{\prime }$. We assume each subject has a common grid of time points across all K entries, such that X and W are common to all subjects, although our proposed method can be generalized to the case where subjects are observed at different grids of time points. In addition, we assume no correlation across different trajectory entries. It should be noted that, although trajectories from the same subject are independent conditional on group, in the next subsection we assume a prior distribution for z_ig, and trajectories from a subject are correlated marginal over z_ig.

To simplify notation, we let $\mathit{S}=[\mathit{X}\hspace{0.17em}\mathit{W}]$ and ${\mathit{\theta }}_g={({\mathit{\alpha }}_{g1}^{\prime },{\mathit{\beta }}_{g1}^{\prime },\dots ,{\mathit{\alpha }}_{gK}^{\prime },{\mathit{\beta }}_{gK}^{\prime })}^{\prime }$. Equation (3.1) can then be rewritten as:

$$\left\{{\mathit{y}}_i\right|z_{ig}=1\}=({\mathit{I}}_K\otimes \mathit{S}){\mathit{\theta }}_g+{\mathit{ϵ}}_i.$$ (3.2)

3.2 Model for the mixing weights

The mixture-of-experts model (Jacobs et al., 1991) is applied to form a covariate-guided structure for our proposed model, where the mixing weights are multinomial logits that are functions of selected covariates. As in Sun et al. (2007), the mixing weights are expressed as

$${\pi }_{ig}({\mathit{V}}_i)=\frac{\hspace{0.17em}\text{exp}({\mathit{V}}_i^{\prime }{\mathit{\delta }}_g+{\zeta }_{ig})}{\sum _{h=1}^G\hspace{0.17em}\text{exp}\hspace{0.17em}({\mathit{V}}_i^{\prime }{\mathit{\delta }}_h+{\zeta }_{ih})},$$ (3.3)

where ${\mathit{V}}_i={(1,V_{i1},\dots ,V_{iP})}^{\prime }$ is a vector of length $(P+1)$ containing values of P covariates for subject i, and ${\mathit{\delta }}_g={({\delta }_{g0},{\delta }_{g1},\dots ,{\delta }_{gP})}^{\prime }$ is the corresponding coefficient vector. For identifiability, we set ${\mathit{\delta }}_G=0$. Equation (3.3) differs slightly from the weights in the traditional mixture of experts model in that it includes a random term ζ_ig for each subject. This term accounts for unmeasured factors beyond the observed covariates and enhances model performance and inference of the mixing weights.

3.3 Augmented likelihood

To account for heterogeneity across subjects, we assume that the kth entry of the multivariate trajectories, ${\mathit{y}}_{ik}$, comes from a mixture model with G components, ie,

$${\mathit{y}}_{ik}\sim \sum _{g=1}^G{\pi }_{ig}{f}_{gk}({\mathit{y}}_{ik}|{\mathit{\mu }}_{gk},{\sigma }_{gk}^2{\mathit{I}}_n),$$ (3.4)

where $f_{gk}({\mathit{y}}_{ik}|{\mathit{\mu }}_{gk},{\sigma }_{gk}^2{\mathit{I}}_n)$ is the probability density function of the multivariate normal distribution with mean vector ${\mathit{\mu }}_{gk}=\mathit{X}{\mathit{\alpha }}_{gk}+\mathit{W}{\mathit{\beta }}_{gk}$ and covariance matrix ${\sigma }_{gk}^2{\mathit{I}}_n$ for the gth component and the kth entry. The π_ig are mixing weights that depend on covariates as described in Section 3.2.

As is common in mixture models, augmenting the likelihood with latent variables indicating the component from which a trajectory originates simplifies the computation greatly (Dempster et al., 1977). In particular, let z_ig = 1 if the ith multivariate trajectory belongs to the gth component and z_ig = 0, otherwise. Let $\mathit{y}={({\mathit{y}}_1,\dots ,{\mathit{y}}_N)}^{\prime }$ be all observed multivariate trajectories and ${\mathbf{\Theta }}_{gk}$ be the aggregation of all parameters for component g and entry k. The parameter vector for all components and all entries is then denoted by $\mathbf{\Theta }={({\mathbf{\Theta }}_{11}^{\prime },\dots ,{\mathbf{\Theta }}_{GK}^{\prime })}^{\prime }$. The augmented likelihood of all N multivariate trajectories is given by

$$L(\mathbf{\Theta }|\mathit{y},Z)=\prod _{i=1}^N\prod _{g=1}^G[{\pi }_{ig}\prod _{k=1}^K{f}_{gk}({\mathit{y}}_{ik}|{\mathbf{\Theta }}_{gk}){]}^{z_{ig}},$$ (3.5)

where $f_{gk}({\mathit{y}}_{ik}|{\mathbf{\Theta }}_{gk})$ is the probability density function as appeared in model (3.4). From Bayes’ rule, the distribution of the latent indicators z_ig is given by

$$p(z_{ig}=1|\mathit{y},\mathit{S},\mathbf{\Theta },{\pi }_{ig})=\frac{{\pi }_{ig}\prod _{k=1}^K{f}_{gk}({\mathit{y}}_{ik}|{\mathbf{\Theta }}_{gk})}{\sum _{h=1}^G{\pi }_{ih}\prod _{k=1}^K{f}_{hk}({\mathit{y}}_{ik}|{\mathbf{\Theta }}_{hk})}.$$ (3.6)

4 Priors

In this section, the priors on the model parameters are introduced.

4.1 Smoothing splines prior

The conditional expectation of a mixture component in model (3.4) is given by $E({\mathit{y}}_{ik}|z_{ig}=1)=\mathit{X}{\mathit{\alpha }}_{gk}+\mathit{W}{\mathit{\beta }}_{gk}$. We place a smoothing spline prior on ${\mathit{\beta }}_{gk}$ and let ${\mathcal{H}}_{gk}=\mathit{W}{\mathit{\beta }}_{gk}$, where ${\mathcal{H}}_{gk}={[{\mathcal{H}}_{gk}(t_1),\dots ,{\mathcal{H}}_{gk}(t_n)]}^{\prime }$ is a zero-mean Gaussian process with variance covariance matrix ${\tau }_{gk}^2\mathbf{\Phi }$ (Wahba, 1980; Wood et al., 2002), such that $\text{cov}[{\mathcal{H}}_{gk}(t_r),{\mathcal{H}}_{gk}(t_h)]={\tau }_{gk}^2{\varphi }_{rh},\hspace{0.17em}{\tau }_{gk}^2$ is a smoothing parameter for component g and entry k, and the (r, h)th element of $\mathbf{\Phi }$ is given by ${\varphi }_{rh}=\frac{1}{2}{t}_r^2(t_h-\frac{t_r}{3})$ for $t_r\le t_h$. The matrix $\mathbf{\Phi }$ is common to all subjects since all entries of the multivariate trajectories are observed at common time points.

As seen above, the matrix $\mathbf{\Phi }$ is n × n, and to avoid the computational burden for large n, a low-rank approximation is often adopted. To facilitate this approximation, we obtain basis functions via the spectral decomposition of $\mathbf{\Phi }$, as has been proposed in Wood et al. (2002) and used in Rosen et al. (2009, 2012); Krafty et al. (2011). In particular, the matrix W consists of m basis functions evaluated at times $t_1,\dots ,t_n$, and ${\mathit{\beta }}_{gk}$ is an m-dimensional vector of basis function coefficients. These basis functions are obtained by applying the spectral decomposition to $\mathbf{\Phi }$ such that $\mathbf{\Phi }=\mathit{Q}\mathbf{\Gamma }{\mathit{Q}}^T$, where Q is the matrix of eigenvectors of $\mathbf{\Phi }$, and $\mathbf{\Gamma }$ is a diagonal matrix containing the eigenvalues of $\mathbf{\Phi }$. We then let the design matrix $\mathit{W}=\mathit{Q}{\mathbf{\Gamma }}^{1/2}$ and place a normal prior $N(0,{\tau }_{gk}^2{\mathit{I}}_n)$ on ${\mathit{\beta }}_{gk}$, which leads to ${\mathcal{H}}_{gk}$ or $\mathit{W}{\mathit{\beta }}_{gk}\sim N(0,{\tau }_{gk}^2\mathbf{\Phi })$ as mentioned above.

By using the low-rank approximation, the number of columns of W is reduced from n to m (m < n), which greatly reduces the computational burden without sacrificing the model fit (Wahba, 1980; Wood, 2006). Eubank (1999) indicated that the eigenvalues in the diagonal matrix $\mathbf{\Gamma }$ decay rapidly as m increases. Thus, we can achieve a good approximation by selecting a relatively small number m of basis functions. The number of basis functions m is set to 10 in simulation studies as described in Section 6, which has been shown (Krafty et al. 2011) to explain more than 98% of the total variability.

We assume the prior ${\mathit{\theta }}_g\sim N(0,{\mathit{D}}_g)$, where ${\mathit{D}}_g=$ diag$({\sigma }_{\alpha 1}^2{1}_2,\hspace{0.17em}{\tau }_{g1}^2{1}_m,\hspace{0.17em}\dots \hspace{0.17em},{\sigma }_{\alpha K}^2{1}_2,\hspace{0.17em}{\tau }_{gK}^2{1}_m)$ is the covariance matrix of ${\mathit{\theta }}_g$. The vector ${({\sigma }_{\alpha 1}^2,\dots ,{\sigma }_{\alpha K}^2)}^{\prime }$ contains fixed prior variances for the regression coefficients ${\mathit{\alpha }}_{gk}$, common to all components and entries. In particular, we fix the common prior variance ${\sigma }_{\alpha }^2=100$. The vector ${\mathit{\tau }}_g^2={({\tau }_{g1}^2,\dots ,{\tau }_{gK}^2)}^{\prime }$ contains the smoothing parameters for the gth mixture component and $1_m$ is an m-vector of ones. We assume independence between the regression coefficients ${\mathit{\alpha }}_{gk}$ and the basis function coefficients ${\mathit{\beta }}_{gk}$.

4.2 Priors on the smoothing parameters

We assume the smoothing parameters ${\mathit{\tau }}_g^2={({\tau }_{g1}^2,\dots ,{\tau }_{gK}^2)}^{\prime }$ vary across components g and entries k. Although the most common choice for the prior on a variance parameter is the inverse gamma distribution, Gelman (2006) and Wand et al. (2011) suggested that a half-t prior on the standard deviation can reflect lack of information on a scale parameter. The half-t is a family of heavy-tailed distributions and has a good shrinkage performance. It can be expressed as a scale mixture of inverse gamma random variables using a latent variable which follows an inverse gamma distribution (Wand et al., 2011). Thus, we assume a half-t distribution such that ${\tau }_{gk}\sim t_{{\nu }_{\tau }}^{+}(0,A_{\tau })$, where ${\nu }_{\tau }$ is a degrees of freedom parameter, and $A_{\tau }$ is a scale parameter. We set ${\nu }_{\tau }=3$ and $A_{\tau }=10$ for all components and entries.

4.3 Priors on the error variances

We assume ${\sigma }_{gk}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}}{\sim }{t}_{{\nu }_{\sigma }}^{+}(0,A_{\sigma })$ and set ${\nu }_{\sigma }=3$ and $A_{\sigma }=10$ for all components and entries.

4.4 Priors on the logistic parameters and the variances of random intercepts

This subsection provides details on the prior distributions placed on the parameters of the logistic weights (3.3). For ease of notation, we denote ${\mathit{\delta }}_g^{*}={({\mathit{\delta }}_g^T,{\mathit{\zeta }}_g^T)}^T$, where ${\mathit{\zeta }}_g={({\zeta }_{1g},\dots ,{\zeta }_{Ng})}^T,\hspace{0.17em}g=1,\dots ,G$. We let ${\mathit{V}}_i^{*}={({\mathit{V}}_i^{\prime },{\mathit{e}}_i^{\prime })}^{\prime }$, where ${\mathit{e}}_i$ is a vector of all zeros except for a single 1 in the ith position, and ${\mathit{V}}^{*}$ is a matrix consisting of the rows ${\mathit{V}}_i^{*T},\hspace{0.17em}i=1,\dots ,N$. Gaussian priors are placed on the logistic parameters, ie, ${\mathit{\delta }}_g^{*}\sim N(0,{\mathit{B}}_g)$, where ${\mathit{B}}_g=\text{diag}({\sigma }_{\delta g}^2{1}_{P+1},\hspace{0.17em}{\kappa }_{\zeta g}^2{1}_N)$, and the priors on the random intercepts satisfy ${\mathit{\zeta }}_g\sim N(0,{\kappa }_{\zeta g}^2{\mathit{I}}_N)$. As for the hyperparameters, we assume ${\sigma }_{\delta g}^2=10$ for all components and covariates, and ${\kappa }_{\zeta g}\sim t_{{\nu }_{\kappa }}^{+}(0,A_{\kappa })$, where ${\nu }_{\kappa }=3$ and $A_{\kappa }=10$ for all components.

To sample the logistic parameters, Polson et al. (2013) proposed a data augmentation scheme incorporating Pólya-Gamma latent variables, which facilitates Gibbs steps. Details on sampling the logistic parameters are provided in the Supplementary Material.

5 Sampling scheme

This section outlines the Gibbs steps for sampling from the conditional posterior distributions of all the model parameters. More details are given in Supplementary Material.

5.1 Gibbs sampling steps

Letting $\ell$ denote the current Gibbs sampling iteration, parameter values at the $(\ell +1)$th iteration are drawn according to the following steps.

1. Draw ${\mathit{\theta }}_{gk}^{(\ell +1)}$ from $({\mathit{\theta }}_{gk}^{(\ell +1)}|\mathit{y},\mathit{S},{\tau }_{gk}^{2(\ell )},{\sigma }_{gk}^{2(\ell )})\sim N({\mathit{u}}_{gk},{\sigma }_{gk}^2{\mathbf{\Lambda }}_{gk})$, where ${\mathit{u}}_{gk}$ and ${\mathbf{\Lambda }}_{gk}$ are mean vectors and covariance matrices.

2. Draw ${\sigma }_{gk}^{2(\ell +1)}$ from $({\sigma }_{gk}^{2(\ell +1)}|{\mathit{ϵ}}_{\mathit{igk}}^{(\ell +1)},a_{{\sigma }_{gk}}^{(\ell +1)})\sim IG((n{N}_g^{(\ell )}+{\nu }_{\sigma })/2,\sum _{i=1}^N{z}_{ig}{\mathit{ϵ}}_{\mathit{igk}}^{\prime }{\mathit{ϵ}}_{\mathit{igk}}/2+{\nu }_{\sigma }/a_{{\sigma }_{gk}})$, where $N_g^{(\ell )}$ is the current number of subjects in the gth component, ${\mathit{ϵ}}_{\mathit{igk}}$ is the error vector for the gth component, the ith subject and the kth entry, and $a_{{\sigma }_{gk}}$ is a latent variable in the IG scale mixture underlying the half-t distribution.

3. Draw ${\tau }_{gk}^{2(\ell +1)}$ from $({\tau }_{gk}^{2(\ell +1)}|{\mathit{\beta }}_{gk}^{(\ell +1)},a_{{\tau }_{gk}}^{(\ell +1)})\sim IG(({\nu }_{\tau }+m)/2,{\mathit{\beta }}_{gk}^{\prime }{\mathit{\beta }}_{gk}/2+{\nu }_{\tau }/a_{{\tau }_{gk}})$, where $a_{{\tau }_{gk}}$ is a latent variable as in 2.

4. Draw ${\mathit{\delta }}_g^{*(\ell +1)}$ from $({\mathit{\delta }}_g^{*(\ell +1)}|{\mathit{V}}^{\mathit{*}},z_{ig}^{(\ell )},{\omega }_{ig}^{(\ell +1)},{\kappa }_{\zeta g}^{2(\ell )})\sim N({\mathit{M}}_g,{\mathbf{\Sigma }}_g)$, where ${\omega }_{ig}^{(\ell +1)}$ is a Pólya-Gamma latent variable in the augmentation described in Section 4.4.

5. Draw ${\kappa }_{\zeta g}^{2(\ell +1)}$ from $({\kappa }_{\zeta g}^{2(\ell +1)}|{\mathit{\zeta }}_g^{(\ell +1)},a_{{\kappa }_g}^{(\ell +1)})\sim IG({\nu }_{\kappa }/2,{\mathit{\zeta }}_g^{\prime }{\mathit{\zeta }}_g/2+({\nu }_{\kappa }+N)/a_{{\kappa }_g})$, where $a_{{\kappa }_g}$ is a latent variable as in 2 and 3.

6. The mixing weights ${\pi }_{ig}^{(\ell +1)}$ are obtained by computing $p({\pi }_{ig}^{(\ell +1)}|{\mathit{V}}^{*},{\mathit{\delta }}_g^{*(\ell +1)},z_{ig}^{(\ell )})$ from (3.3).

7. Draw $z_{ig}^{(\ell +1)}\sim p(z_{ig}^{(\ell +1)}=1|\mathit{y},\mathit{S},{\mathit{\theta }}_{gk}^{(\ell +1)},{\sigma }_{gk}^{2(\ell +1)},{\pi }_{ig}^{(\ell +1)})$ according to (3.6).

5.2 Selecting the number of components

Spiegelhalter et al. (2002) suggested the use of the deviance information criterion (DIC) for model selection based on the effective number of parameters. Gelman et al. (2003) introduced an alternative measure of effective number of parameters based on the variance of the log predictive density across MCMC iterations. This measure is robust and more accurate than the original one. Moreover, it has the advantages of always being positive and invariant to reparameterizations (Gelman et al., 2003).

In this article, we use DIC to select the number of components for our proposed mixture model.

6 Simulation studies

To demonstrate the performance of the proposed method, we conduct simulation studies by generating data sets from the proposed model under two scenarios: two-component mixture (G = 2) of trivariate trajectories (K = 3) and four-component mixture (G = 4) of bivariate trajectories ($K=2)$. We simulate 100 replicates in each simulation setting with N = 150 trajectories of length n = 50. A total of 20, 000 Gibbs sampling iterations are run with a burn-in of 4, 000. In all simulation settings, the hyperparameters are assigned the same values, given in Section 4.

6.1 Two-component trivariate model

In this scenario, we consider the two-component trivariate model. From (3.1), the gth component of the proposed mixture model is given by

$$\{{\mathit{y}}_i(t_j)|z_{ig}=1\}={\mathit{\alpha }}_{0g}+{\mathit{\alpha }}_{1g}{t}_j+\sum _{q=1}^m{w}_q(t_j){\mathit{\beta }}_{gq}+{\mathit{ϵ}}_{ig{t}_j},\hspace{1em}j=1,\dots ,n,\hspace{0.17em}\hspace{0.17em}g=1,\dots ,G,$$ (6.7)

where ${\mathit{y}}_i(t_j)$ is the trivariate trajectories of subject i evaluated at time t_j, ${\mathit{\alpha }}_{01}={(1,-3,-2)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{02}=(5,4,3)$, and ${\mathit{\alpha }}_{11}={(-2,2,0.5)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{12}={(1,-1,-0.5)}^{\prime }$ are independent intercepts and slopes for each component, respectively. The vector ${\mathit{\beta }}_{gq}$ consists of the qth spline coefficients of all variates for component g, and $w_q(t_j)$ is the qth spline basis function evaluated at time t_j. The ${\mathit{ϵ}}_{ig{t}_j}$ are independent zero-mean error terms, distributed as ${\mathit{ϵ}}_{ig{t}_j}\sim \text{MVN}(0,\text{diag}({\sigma }_{g1}^2,{\sigma }_{g2}^2,{\sigma }_{g3}^2))$, where ${\sigma }_1^2={({\sigma }_{11}^2,{\sigma }_{12}^2,{\sigma }_{13}^2)}^{\prime }={(3,5,4.5)}^{\prime }$ and ${\sigma }_2^2={({\sigma }_{21}^2,{\sigma }_{22}^2,{\sigma }_{23}^2)}^{\prime }={(4,3.5,4)}^{\prime }$. The smoothing parameters are set to ${\tau }_1^2={({\tau }_{11}^2,{\tau }_{12}^2,{\tau }_{13}^2)}^{\prime }={(3.5,5,8.5)}^{\prime }$ and ${\tau }_2^2={({\tau }_{21}^2,{\tau }_{22}^2,{\tau }_{23}^2)}^{\prime }={(6,2.5,1.5)}^{\prime }$.

We investigate the performance of the trajectory and logistic parameter (see (3.3)) estimates. For the former, we calculate the averaged root square error (ARSE) of each mixture component g

$${\text{ARSE}}_g=\sqrt{\frac{1}{nK}\sum _{j=1}^n\sum _{k=1}^K[{\mu }_{gk}(t_j)-{\widehat{\mu }}_{gk}(t_j){]}^2},$$

where ${\mu }_{gk}(t_j)$ is the expectation of $y_{ik}(t_j)$ according to the gth component, and $y_{ik}(t_j)$ is the kth entry of the trajectories evaluated at time t_j for subject i. The ${\widehat{\mu }}_{gk}(t_j)$ are the estimated posterior means of ${\mu }_{gk}(t_j)$ for $k=1,\dots ,K$ and $j=1,\dots ,n$.

To handle a potential label switching across mixture components, we compute ${\text{ARSE}}_g$ as the minimum value across all components, by using the estimate of the gth component and the truth of each group, $g=1,\dots ,G$. After obtaining correct component labels by evaluating ARSE, we also report the averaged bias (A-bias) and the variance of the bias (V-bias) of each mixture component g, where

$${\mathrm{A}-\text{bias}}_g=\frac{1}{nK}\sum _{j=1}^n\sum _{k=1}^K[{\widehat{\mu }}_{gk}(t_j)-{\mu }_{gk}(t_j)],$$

and ${\mathrm{V}-\text{bias}}_g$ is computed by calculating the sample variance of the bias over entries and time points.

For each replicate, trajectories are estimated by three methods: the proposed method, the $\mathtt{R}$ package $\mathtt{gbmt}$ (Magrini, 2022) and the $\mathtt{TRAJ}$ procedure in SAS (Nagin et al., 2018). Boxplots of ARSE, A-bias and V-bias of each component are given in the first row of Fig. 2. Notably, $\mathtt{TRAJ}$ is able to fit a regression spline model by treating basis functions as time-varying covariates, while $\mathtt{gbmt}$ is only able to fit a cubic model. Our proposed method fits a penalized spline model under the Bayesian framework and is able to outperform both $\mathtt{gbmt}$ and $\mathtt{TRAJ}$ in terms of ARSE and V-bias for both components. A-biases are close to zero and comparable for all three methods. These findings demonstrate that all three methods are able to achieve a reasonable fit to group-based trajectories since bias over the entire trajectories is close to zero. Our proposed method is able to obtain more precise estimates of trajectories as is evident from the smaller V-biases.

Fig. 2.

Boxplots of the averaged root square error (ARSE), the averaged bias (A-bias), and the variance of the bias (V-bias) of the estimated trajectories for each component from 100 replicates of 150 two-component trivariate trajectories of length 50 (first row) and from 100 replicates of 150 four-component bivariate trajectories of length 50 (second row). The proposed method was compared to R package gbmt and TRAJ procedure in SAS. The diamond markers denote the mean statistics of each method and component. All boxplots are zoomed in for better visualization.

To evaluate the performances of the logistic parameters, we compute the root mean squared error (RMSE) for each logistic parameter using the proposed method and $\mathtt{TRAJ}$. Notably, $\mathtt{gbmt}$ is not able to incorporate covariates into the computation of mixing weights. Results of RMSEs of each logistic parameter are given in Table 1. We also compare RMSEs between the proposed method and $\mathtt{TRAJ}$ under four settings of different combinations of N = 150, 250 and n = 50, 70. Our proposed method yields smaller RMSEs of the logistic parameters in all cases, especially for the intercept δ₀ and the first covariate δ₁. This is to be expected since $\mathtt{TRAJ}$ uses a multinomial logistic model, which may result in inflated parameter estimates in cases of unbalanced outcomes or perfect separation, while our proposed method is able to obtain a shrinkage result using the penalization method.

Table 1.

Root mean square errors (RMSEs) of each logistic parameter for the two-component trivariate model from 100 replicates of N two-component trivariate trajectories of length n, and the four-component trivariate model with N = 150 and n = 50. RMSEs of the proposed method were compared to TRAJ procedure in SAS. Parameters δ₀, δ₁, δ₂, and δ₃ are intercept, first, second, and third logistic parameters, respectively. For the two-component trivariate model, the second component is used as the reference component. The true values of the logistic parameters are $5,-3.5,1,0.1$, respectively. For the four-component bivariate model, the fourth component is used as the reference component. The true values of the logistic parameters are $5,-3.5,1,0.1$ (first component), $-4,2.5,-2,-0.2$ (second component), $3,-2,0.8,0.2$ (third component). C1, C2, C3, and C4 denote first, second, third, and fourth component, respectively.

True model	n	N	Method	Comparison	δ 0	δ 1	δ 2	δ 3
Two-component, trivariate	50	150	Proposed	C1 vs C2	0.89	0.52	0.29	0.32
			TRAJ	C1 vs C2	1.57	0.87	0.36	0.34
	70	150	Proposed	C1 vs C2	0.86	0.50	0.29	0.31
			TRAJ	C1 vs C2	1.55	0.86	0.36	0.34
	50	250	Proposed	C1 vs C2	0.77	0.40	0.22	0.23
			TRAJ	C1 vs C2	0.96	0.50	0.23	0.24
	70	250	Proposed	C1 vs C2	0.77	0.41	0.22	0.23
			TRAJ	C1 vs C2	0.97	0.51	0.24	0.24
Four-component, bivariate	50	150	Proposed	C1 vs C4	0.81	0.53	0.30	0.39
				C2 vs C4	1.11	0.46	0.42	0.36
				C3 vs C4	0.89	0.42	0.28	0.34
			TRAJ	C1 vs C4	1.20	0.74	0.35	0.41
				C2 vs C4	3.81	2.27	1.33	0.49
				C3 vs C4	2.07	1.33	0.76	0.32

6.2 Four-component bivariate model

In this scenario, we consider the four-component bivariate model whose gth component is given in (6.7), where the values of the intercepts and slopes are ${\mathit{\alpha }}_{01}={(1,-2)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{02}={(5,3)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{03}={(-3,5.5)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{04}={(4,-1)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{11}={(-3,0)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{12}={(2,-3.5)}^{\prime },\hspace{0.17em}{\mathit{\alpha }}_{13}=(2.5,2)$, and ${\mathit{\alpha }}_{14}={(-3,1.5)}^{\prime }$. By analogy to the two-component trivariate model, the errors ${\mathit{ϵ}}_{ig{t}_j}$ are independent zero-mean bivariate Gaussian random variables, distributed as ${\mathit{ϵ}}_{ig{t}_j}\sim \text{MVN}(0,\text{diag}({\sigma }_{g1}^2,{\sigma }_{g2}^2))$, where ${\sigma }_1^2={({\sigma }_{11}^2,{\sigma }_{12}^2)}^{\prime }={(6,9)}^{\prime },\hspace{0.17em}{\sigma }_2^2={({\sigma }_{21}^2,{\sigma }_{22}^2)}^{\prime }={(8,7.5)}^{\prime },\hspace{0.17em}{\sigma }_3^2={({\sigma }_{31}^2,{\sigma }_{32}^2)}^{\prime }=(10,6.5)$, and ${\sigma }_4^2={({\sigma }_{41}^2,{\sigma }_{42}^2)}^{\prime }={(7,8.5)}^{\prime }$.

The performances of the estimated trajectories and logistic parameters for this scenario are displayed in the second row of Fig. 2 and Table 1. As in the first scenario, our proposed method outperforms both gbmt and TRAJ in terms of ARSE and V-bias for all components. Notably, TRAJ fails to yield precise estimates in several replicates and thus results in larger mean ARSE and V-bias. In terms of the logistic parameters, the proposed method performs well with smaller RMSEs in almost all cases, especially for δ₀ and δ₁. More simulation results based on different values of N and n under the two scenarios considered above, as well as a simulation of a two-component four-variate model closely matching our real data dimension and component settings, are presented in the Supplementary Material.

7 Real data application

We apply our proposed method to the analysis of the fNIRS still-face study introduced in Section 2. Six covariates are considered in our covariate-guided model: Infant Behavior Questionnaire-Revised negative emotionality (IBQ-NE) score, Infant Behavior Questionnaire-Revised effortful control (IBQ-EC) score, gestational age (in Days), infant age (in Months), head circumference (in cm), and sex. All continuous covariates are centered and scaled. We set the number of basis functions at m = 20 and run a total of 30, 000 Gibbs iterations with a burn-in period of 6, 000. The values of the hyperparameters are the same as the ones used in the simulation studies.

The IBQ-NE construct combines data from the following subscales: Sadness, Distress to Limitations, Fear, and Falling Reactivity/Rate of Recovery from Distress. IBQ-EC refers to the ability to inhibit a dominant response to perform a subdominant one and has been shown to be protective against a myriad of difficulties (Gartstein et al., 2013). Finally, the data consist of 79 subjects with complete fNIRS and covariate values. We present results based on analyzing one set of four-channels in the prefrontal cortex, which plays important roles in regulating behavior and emotions. Additional results based on analyzing another set of four channels and all channels are given in the Supplementary Material. The four channels are S1D1, S2D2, S5D3, and S6D4, the data from which is displayed in Fig. 1. We fit our proposed model with the number of components varying from 2 to 6. Based on values of DIC introduced in Section 5.2, the two-component model is selected as the best model for this four-channel analysis.

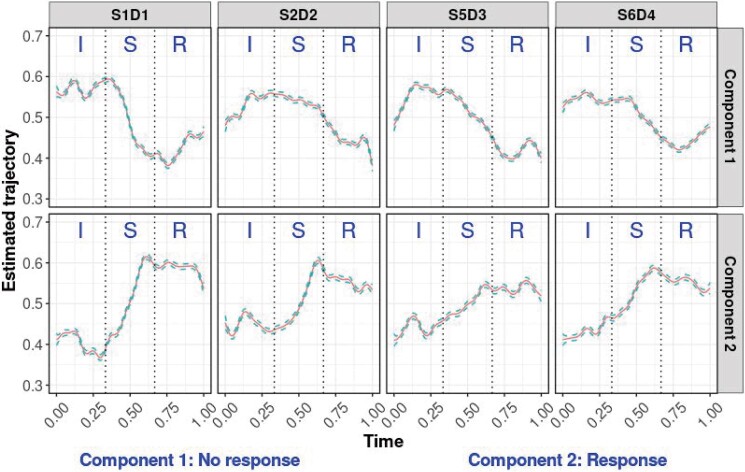
Figure 3 presents the estimated trajectories of the two-component model fitted to the four channels. We are interested in brain activity signals in the still-face period while the interact period is used as the reference level. For component 1, a decreasing trajectory is observed for the still-face period in all four channels. In contrast, an increasing trend is observed for the still-face period in all four channels for component 2. Trajectories from the two-component model show consistency of brain activity levels across different brain functional areas and demonstrate the heterogeneity of brain activity patterns in the population. After fitting the mixture model and finding the above trajectory patterns, we define component 1 as the no-response component and component 2 as the response component based on trajectory patterns in the still-face period. Figure 4 displays the logistic parameter estimates for all covariates in the 2-component model, where component 2 is used as the reference. There is evidence that IBQ-NE scores differ between the two components. A positive coefficient of IBQ-NE indicates that a higher IBQ-NE score is associated with decreased brain activity in the still-face period for all four channels. Infants who are highly susceptible to sadness and fear tend to be less responsive to the violation of the expectation of social interaction. The negative posterior mean estimate of the IBQ-EC score indicates that a high IBQ-EC is associated with an increased brain activity. Infants who are resilient to difficulties tend to be more responsive when the expectation of social interaction is not met. The above conclusions are consistent with findings in Gartstein et al. (2013) that IBQ-NE is negatively associated with IBQ-EC. Enlow et al. (2016) reported a negative association between activity level and IBQ-NE among infants whose families encourage a high level of activities. Furthermore, a negative posterior mean of the logistic coefficient of infant age suggests that age could play an important role where younger infants tend to be less responsive to the FFSF paradigm.

Fig. 3.

Estimated posterior mean and 95% credible intervals of trajectories of the two-component model with four selected channels. I: Interact S: Still-face R: Recovery.

Fig. 4.

Logistic coefficient estimates and 95% credible intervals for each covariate of the two-component model.

8 Discussion

The proposed covariate-guided Bayesian mixture of spline experts model aims to perform a model-based clustering of multivariate high-density longitudinal data from multiple subjects. Our proposed method is compared to two commonly used methods through simulation studies which demonstrate a better performance of our method under different scenarios. We apply our proposed method to a fNIRS still-face study and find distinct patterns of components of longitudinal trajectories, as well as an association between IBQ-NE score and a pattern of decreased brain activity in the still-face period. To the best of our knowledge, this is the first still-face study using fNIRS whose purpose is to identify trajectory components.

Our proposed method provides posterior estimates through a Gibbs sampling algorithm. Trace plots for the various parameters indicate convergence of the algorithm with good mixing. Examples of trace plots of the logistic parameters for the four-channel analysis presented in Section 7 are given in the Supplemental Material. As for model performance, the Widely Applicable Information Criterion (WAIC) is commonly used as a metric to compare Bayesian model performance (Watanabe and Opper, 2010). We compute both DIC and WAIC for the two simulation studies in Section 6.1 as well as Section 6.2 for selecting the number of mixture components. Consistent results are achieved from DIC and WAIC for both simulations as shown in the Supplemental Material. In addition, interpolation is performed in the preprocessing step of the fNIRS data. Though this signal interpolation has very little impact on our trajectory analysis, it does have significant impact on analyses that focus on autocorrelation and spectral structure. Thus, interpolation must be used with caution, especially if being used in other setting where one desires an analysis to conduct inference on second-order properties.

Our proposed method has several limitations. First, as in any mixture models, label switching may occur, especially in the real-data application. We have adopted the Equivalence Classes Representatives (ECR) algorithm proposed by Papastamoulis and Iliopoulos (2010) to make the components interpretable, but other methods may be considered. Second, although trajectory entries from the same subject are correlated marginal over group, they are independent conditional on group so that spatial dependence among different fNIRS channels is not modeled within group. An extension to a multivariate functional ANOVA model (Zhang et al., 2023) or a multivariate functional model with a prespecified spatial correlation structure (Baladandayuthapani et al., 2008) would be possible by considering spatial correlations among trajectory entries. Thirdly, large logistic parameter uncertainties, indicated by wide 95% credible intervals, are observed in the real data analysis. Future studies with larger sample sizes and more covariates are needed to confirm our findings and reduce any unmeasured uncertainties in predicting the mixing weights. Lastly, our proposed method uses DIC to select the number of components which might be sub-optimal. Bayesian model averaging and reversible jump MCMC (RJMCMC) methods could be considered, but transdimensional sampling methods would pose challenges in providing interpretable components.

9 Software

Software in the form of R codes, along with an example dataset, is available at https://github.com/HaoyiFu1993/CBMOSE.

Funding

This project was supported by grants funded by the National Institutes of Health (OD023244, R01GM113243).

Conflict of interest statement

None declared.