Evaluating well-mixed room and near-field–far-field model performance under highly controlled conditions

Abstract

Exposure judgments made without personal exposure data and based instead on subjective inputs tend to underestimate exposure, with exposure judgment accuracy not significantly more accurate than random chance. Therefore, objective inputs that contribute to more accurate decision making are needed. Models have been shown anecdotally to be useful in accurately predicting exposure but their use in occupational hygiene has been limited. This may be attributable to a general lack of guidance on model selection and use and scant model input data. The lack of systematic evaluation of the models is also an important factor.

This research addresses the need to systematically evaluate two widely applicable models, the Well-Mixed Room (WMR) and Near-Field–Far-Field (NF-FF) models. The evaluation, conducted under highly controlled conditions in an exposure chamber, allowed for model inputs to be accurately measured and controlled, generating over 800 pairs of high quality measured and modeled exposure estimates. By varying conditions in the chamber one at a time, model performance across a range of conditions was evaluated using two sets of criteria: the ASTM Standard 5157 and the AIHA Exposure Assessment categorical criteria.

Model performance for the WMR model was excellent, with ASTM performance criteria met for 88–97% of the pairs across the three chemicals used in the study, and 96% categorical agreement observed. Model performance for the NF-FF model, impacted somewhat by the size of the chamber was nevertheless good to excellent. NF modeled estimates met modified ASTM criteria for 67–84% of the pairs while 69–91% of FF modeled estimates met these criteria. Categorical agreement was observed for 72% and 96% of NF and FF pairs, respectively. These results support the use of the WMR and NF–FF models in guiding decision making towards improving exposure judgment accuracy.

Introduction

When decisions regarding the acceptability of occupational exposure are based on professional judgment informed by subjective inputs, they are accurate ∼30% of the time and tend to underestimate the true exposure.^[1–3] However, when professional judgment is informed by structured, objective inputs such as statistical analyses of exposure monitoring data^[1] or algorithms and checklists,^[3] they tend to be significantly more accurate.

Anecdotal reports suggest that the use of exposure models such as deterministic physical-chemical models contribute to accurate decision making, but these models are not widely used in practice. Possible reasons for this might be that these models have not been systematically evaluated, there is scant guidance on how to select them, and a lack of model input values to apply the models. Thus, models tend to be under-valued and under-utilized, especially in the practice of occupational hygiene.

Models have been applied across a broad range of fields to improve decision making, from weather forecasting to medical diagnosis and treatment selections.^[4–8] Meehl^[9] asserted that models consistently produce significantly more accurate judgments than subjective expert judgments. Since then, nearly 200 studies have been conducted that support this assertion.^[8] The range of predicted outcomes has expanded to include economic indicators, career satisfaction of workers, questions of interest to government agencies, and the future price of Bordeaux wines. Pharmaceutical researchers use simple models based on readily available inputs, identifying potential candidate compounds for transdermal drug^[10] and oral drug delivery.^[11] The Apgar test, a simple model comprising five critical determinants has been helping save the lives of neonates since 1953.^[4,8] These fields have in common a significant degree of uncertainty and unpredictability, which Kahneman^[8] refers to as “low-validity.” The application of mathematical models to the low-validity field of occupational hygiene exposure assessment is a logical next step towards improving exposure judgments.

There are several deterministic models with varying levels of sophistication^[12,13] and correspondingly varying costs of obtaining high quality model input values. For example, the near field-far field model requires knowledge of room ventilation and contaminant generation rates in addition to the model input, the inter-zonal ventilation rate—involving a non-trivial investment. A sophisticated eddy diffusion model, which accounts for concentration gradients around pollution sources, requires even greater investments. While costs increase with the level of sophistication, more complex models can also yield more refined exposure estimates.

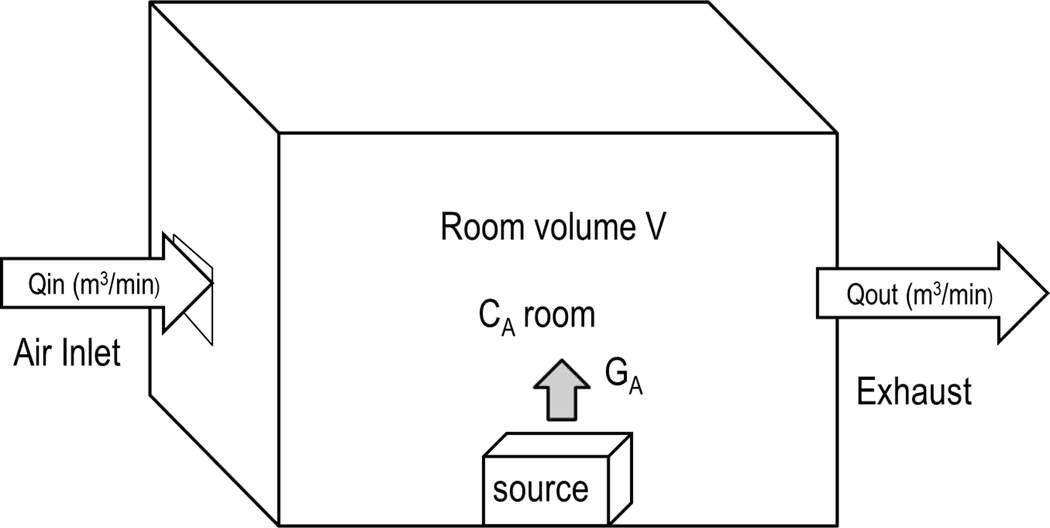
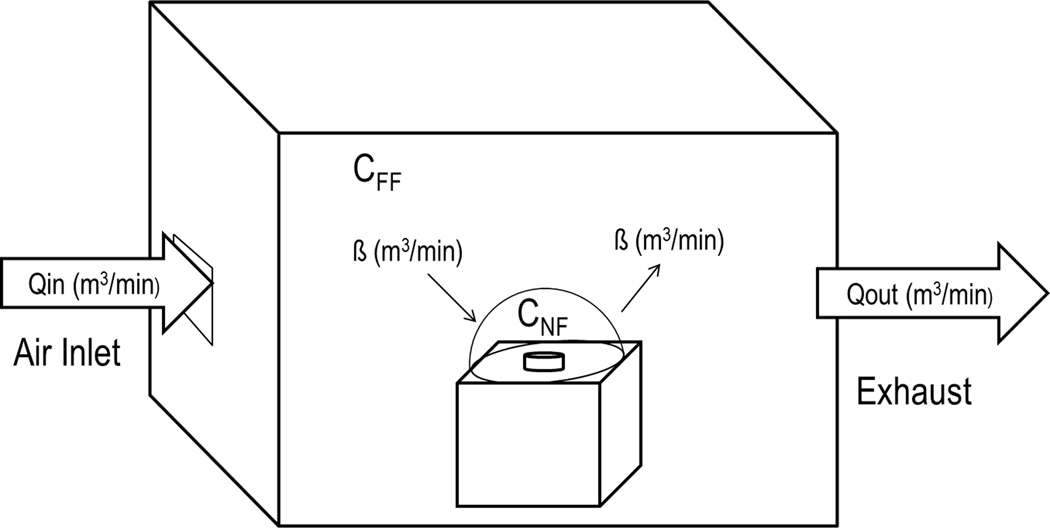
We evaluated two models, the Well-Mixed Room (WMR) and the Two Zone or Near-Field–Far-Field (NF–FF) models in a series of studies conducted in a full-sized exposure chamber using criteria defined in ASTM 5157 and categorical criteria defined in the AIHA Exposure Assessment Strategies framework.^[14–16] The WMR and NF–FF models were selected for evaluation, having broad applicability in assessing both occupational and non-occupational exposures. These models, described in detail elsewhere^[12,17] and briefly presented in the online Supplemental Materials, assume that the chemical released into the air (G) is instantaneously well mixed in one or two boxes. The WMR model, illustrated in Figure 1a assumes a one-box geometry. Air entering the room (Q) is instantaneously well mixed, so that the contaminant concentration (C) is uniformly dispersed throughout the room. The NF–FF model, shown in Figure 1b, assumes a box-within-a-box geometry, accounting for spatial differences in the magnitude of exposure associated with point source emissions. It assumes that the air and contaminant concentration within each box is well mixed, with the same assumption regarding the rate at which air enters and is exhausted from the room. The model is premised on an additional assumption regarding the rate at which the contaminant concentration in the NF moves to and from the FF. This assumption is accounted for in the model by the interzonal airflow rate, $\beta$. The chamber setup in this work was arranged to account for these fundamental assumptions.

Figure 1a.

Well-Mixed Room model schematic showing key model inputs. Generation Rate, ${\text{G}}_{\text{A}}$; Ventilation Rate, Q; Airborne rom contaminant concentration, $C{A}_{room}$.

Figure 1b.

Near–Field–Far–Field model schematic, showing the additional box, accounting for spatial differences in exposure between the Near-Field contaminant concentration, CNF and the Far–Field contaminant concentration, CFF due to a point source and including the additional model input Interzonal airflow rate, and $\beta$, accounting for imperfect mixing.

Methods

A series of chamber studies were conducted to evaluate model performance under controlled conditions that were changed systematically so that model performance could be evaluated across a range of environmental conditions. The highly controlled environment also facilitated evaluation of different models under similar conditions, providing insight into whether one model provides a more accurate exposure estimate for a given set of conditions.

Chamber design

A full-size exposure chamber (2.0 m × 2.8 m × 2.1 m) was constructed for this research. A detailed description of the chamber construction is presented in the Supplemental Materials.

Precise generation rates, G (mg/min), were achieved by releasing a solvent into the chamber using a Harvard Apparatus^® Pump, Series 11 Elite, (Harvard Apparatus, Holliston, MA) equipped with a Becton Dickenson 30 mL or 50 mL glass syringe (East Rutherford, NJ). Because of the relatively high vapor pressures, the solvents evaporated almost immediately upon delivery, emitting the solvent vapor at a known and consistent generation rate.

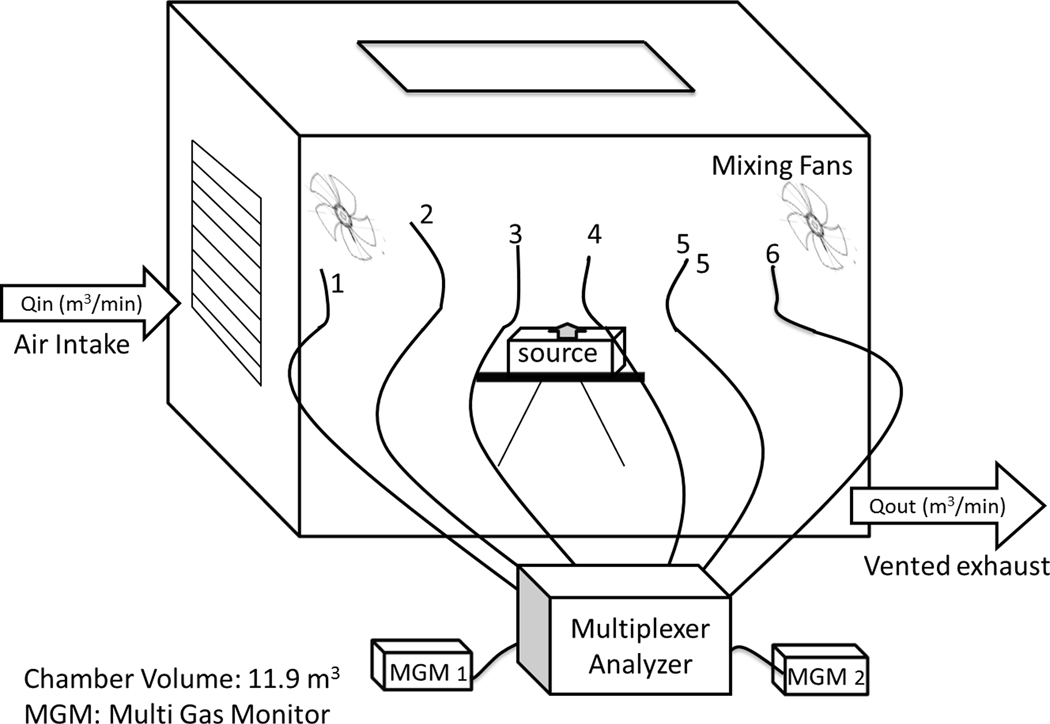
Ventilation rates, Q (m³/min), were controlled using a combined orifice and damper system located in the exhaust duct. Concentration decay data were used to verify air exchange rates (ACH), measuring the concentration in the chamber following cessation of solvent generation and as the contaminated air was replaced with fresh air at the conclusion of every test at each of the six sample locations, (Table 1 and Figure 2). The decay study was used to estimate the actual ventilation rate (or ACH) for the experiment. ACH were estimated using the conventional method[18] using a log-linear regression based on decay data.

Table I.

Sampling locations in the chamber relative to the contaminant source for the WMR tests

Sampling Location	Position Relative to Source	Distance from Source, m
		X direction	Y direction	Z direction
1	Upstream	0.03	1.27	0.52
2		0.61	1.14	0.20
3		0.67	0.25	0.41
4	Downstream	0.03	0.2	0.41
5		0.00	0.74	0.39
6		0.06	1.3	0.58

Figure 2.

Full-size exposure chamber arrangement for WMR studies with six sampling locations throughout the chamber and source centrally positioned. Qin: ventilation rate of air entering the chamber; Qout: ventilation rate of air leaving chamber.

A Magnehelic^® differential pressure gauge (Dwyer Instruments Inc., Michigan City, IN) was used to measure the pressure differential across the orifice located in the ventilation duct and thus ensure relatively consistent air exchange rates across tests.

To induce good mixing in the chamber, two Air King adjustable-height 3-speed fans equipped with tilting heads (W.W. Grainger, Inc., www.grainger.com) were placed in opposite corners of the chamber facing the corners and set on the lowest fan speed.

Chamber study design for WMR model evaluation

Three industrial solvents—toluene, 2-butanone, and acetone—were selected due to their widespread industrial application and range of vapor pressures. Solvent properties are shown in Table 2.

Table II:

Solvent properties of the three solvents used in the chamber study

Solvents	MW	Vapor Pressure @ 25 degrees C	Density g/ml
Toluene	92.11	28 mm Hg	0.864
2-Butanone	84.93	71 mm Hg	0.805
Acetone	58.08	200 mm Hg	0.791

A factorial study design was used to evaluate the WMR and NF–FF models across a range of emission and ventilation rates. Solvent injection rates (of 0.05 mL/min, 0.1 mL/min and 0.15 mL/min) were selected to accommodate instrument sensitivity, delivery capacity and time required to approach steady state concentrations. Three ventilation rates (Q) of ∼ 0.3, 1.3, and 3 ACH corresponding to 0.04–0.07 m³/min, 0.23–0.27 m³/min, and 0.47 – 0.77 m³/min were used, representing ranges relevant to residential and industrial settings. Each set of chamber studies was repeated 3 times. Thus, for each solvent, 3 generation rates x 3 ventilation rates x 3 repetitions = 27 studies were conducted. Generation and ventilation rates are shown in Table 3.

Table III:

Solvent generation rates and ventilation rate ranges. Generation rates corresponding to delivery volumes 0.05, 0.1 and 0.15 ml/min.

Solvent	Generation Rate, G (mg/min)			Ventilation Rate, Q (m3/min)
	low	med	high	Low	med	high
Toluene	43.2	86.4	129.6
2-Butanone	40.3	80.5	120.8	0.04 – 0.07	0.23 – 0.27	0.47– 0.77
Acetone	39.6	79.1	118.7

Solvent vapor concentrations, hereafter referred to as ${\text{C}}_{\text{measured}}$, were measured in real-time using two Dräger X-am 7000 Multi-Gas Monitors (MGM) equipped with Smart PID sensors (Dräger Safety AG & Co. KGaA). Each instrument was calibrated according to the manufacturer’s instructions using a standard calibration gas of 100 ppm isobutylene (Dräger Safety AG & Co. KGaA). To ensure the most accurate results, additional calibration studies were conducted with each MGM, verifying the response factor for the three solvents. These studies are described further in the Supplemental Materials. In the WMR studies, real-time contaminant measurements (${\text{C}}_{\text{measured}}$) were collected at six locations in the chamber (Table 1 and Figure 2)—three upstream and three downstream. Two MGMs, both located outside the chamber were connected to a multiplexer, an instrument fitted with switch valves that were controlled using software to determine the open/close, frequency, and duration sequence. On the other side of the multiplexer six lengths of copper tubing were connected, each one fed through a dedicated port in the chamber wall and positioned in the chamber at various locations (Figure 2). For the WMR studies, measurements were collected concurrently at one location upstream and downstream of the source, with each instrument capturing three 10-s average measurements before the valves controlling those locations closed and a new set of valves opened, allowing the next locations (one upstream and one downstream) to be sampled. Following this pattern, each location was sampled every 1.5 min. The sampling distances from the source for each location are shown in Table 1.

The initial contaminant concentration (${\text{C}}_0$) and contaminant concentration in the incoming air, ${\text{C}}_{\text{in}}$ were also measured directly using the MGMs. Since the incoming air was filtered and contaminant-free, ${\text{C}}_{\text{in}}$ was equal to zero. ${\text{C}}_0$ was typically zero, but when the initial concentration was greater than zero, ${\text{C}}_0$ was adjusted accordingly.

The WMR model includes a loss term $k_{\text{L}}$, that is useful for accounting for pollutant mass loss due to mechanisms such as pollutant degradation or adhesion to surfaces such as the chamber walls or copper tubing surfaces. $k_{\text{L}}$ was determined from empirical studies to be $<0.01$ (see Supplementary Materials for a description of how $k_{\text{L}}$ was calculated).

Chamber study design for the NF–FF model evaluation

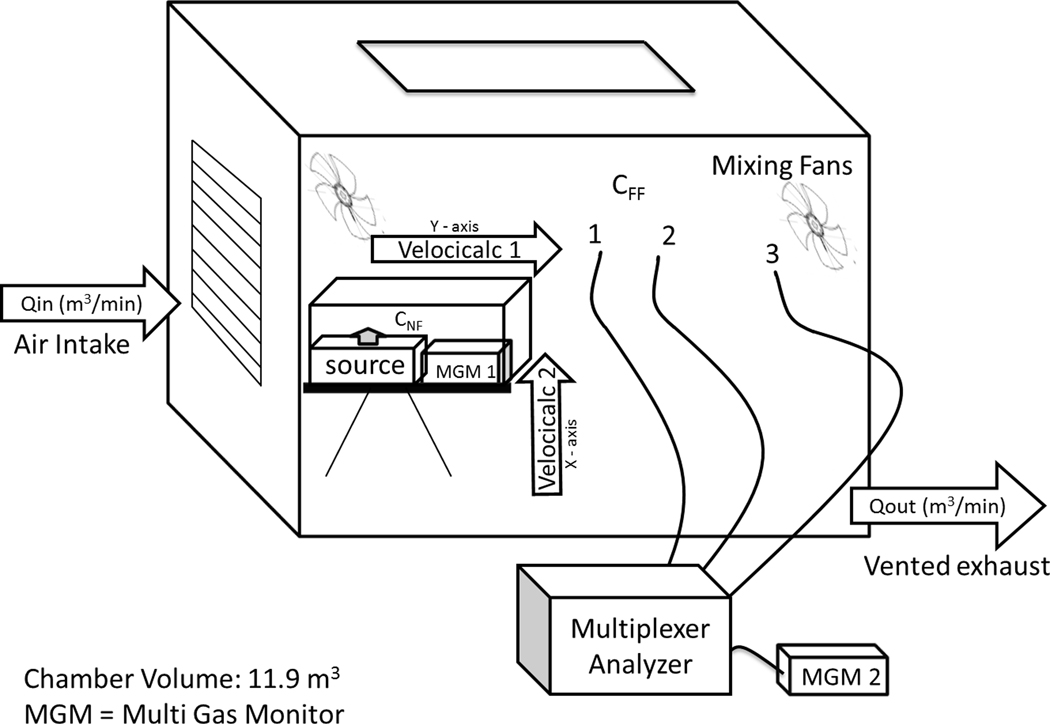
The NF-FF model assumes the Near-Field (NF), the area encompassing the source is a well-mixed box situated within a larger well-mixed box, the Far-Field (FF). While the NF is typically a conceptual space and not necessarily defined by physical barriers, our NF box was constructed from perforated wire mesh. This box was sized (0.51 × 0.51 × 0.41 $\text{m}=0.105{\text{m}}^3$) to ensure that the differences in the magnitude of exposure were large enough to be detected by the MGM. The FF volume represents the chamber volume minus the NF volume = 11.79 m³. The NF with the source inside of it was placed 0.6 m downstream of the air inlet. To ensure the instrument’s sensors detected the rapidly increasing concentration close to the source, one of the MGM was placed inside the NF box, 0.2 m from the source. Since this instrument was inside the chamber, sampling was conducted ata single location and thus only one sample was collected in the NF for each test. FF measurements were collected in the same manner as the WMR studies, at the same locations. Thus, for the FF, three samples were collected for each test (Figure 3).

Figure 3.

Exposure Chamber – NF–FF Configuration showing arrangement in the chamber for the NF–FF model. FF sampling locations correspond to WMR sampling locations 4, 5, and 6, respectively.

The same ventilation rates and generation rates used in the WMR studies were also used for the NF–FF model evaluation. Decay data were collected following the same protocol to measure Q at each sample location.

According to the model, air within the NF and FF is assumed to be instantaneously well mixed, with air movement between the two zones. The rate at which air, and any contaminant in the air, moves from the NF to the FF and vice versa is characterized by the inter-zonal airflow rate, $\text{ß}$. Unlike the other model inputs, $\beta$ cannot be measured directly. It is estimated by accounting for the effects of the NF geometry and local air speed.

$$\beta =1/2\times \text{FSA}\times \text{S}$$ (1)

where FSA is the Free Surface Area of the NF (m²), and S is the random local air speed (m/min).[17] Since the NF in these studies was a box with all six sides open to air movement, the free surface area was calculated by summing the area across the six sides of the box. The FSA was 1.34 m².

Local air speed measurements were collected every 30 sec along thex and y-axes in the chamber during each test and data-logged, using two TSI Velocicalc model 9545 thermal anemometers (TSI Inc., Shoreview, MN). The standard deviations of the air speed measurements along each of the x- and y-axes were taken to be the random air speeds along those axes.^[19] Since measurements were not collected along the z-axis, the standard deviations along the x- and y-axis were averaged to estimate the air speed along the z-axis. An overall average local air speed was calculated from the square root of the summed squares of ${\text{S}}_{\text{x}}$, ${\text{S}}_{\text{y}}$, and ${\text{S}}_{\text{z}}$:

$$S_{x,y,z}=\sqrt{s_x^2+s_y^2+s_z^2}$$ (2)

Values for $\text{β}$ varied according to the variability in the local air speed for each test and ranged from 0.24–1.24 m³/min.

Model evaluation criteria

To compare model performance of each model under a range of conditions and compare performance of the two models for a specific set of conditions, ASTM 5153–97 criteria were used.^[20] These statistics were applied to each set of measured and modeled exposure estimates. In other words, model performance was evaluated separately for each test. General concordance between measured and modeled time-varying concentrations for each model was evaluated using the correlation coefficient, $r$, and the line of regression. The degree of concordance ranges from −1 to 1 with a value of 1 indicating a strong, direct relationship, a value of 0 indicating no relationship, and a value of −1 indicating a strong, inverse relationship:

$$r=\frac{{\sum }_{i=1}^n\left[\left(C_{oi}-{\overline{C}}_o\right)\left(C_{pi}-{\overline{C}}_p\right)\right]}{\sqrt{{\sum }_{i=1}^n\left[{\left(C_{oi}-{\overline{C}}_o\right)}^2\right]\left[\sum _n^{i=1}{\left(C_{pi}-{\overline{C}}_p\right)}^2\right]}},$$ (3)

where $C_{oi}$ is the ${\text{C}}_{\text{observed}}$ for the ith Concentration value $C_{pi}$ is the ith ${\text{C}}_{\text{modeled}}$ for the ith test, ${\overline{C}}_o$ and ${\overline{C}}_{\text{p}}$ are averages, for example, ${\overline{C}}_o={\sum }_i^n\frac{C_{oi}}{n}$, where $n$ is the number of observed values in the test data set.

A line of best fit, with slope $b$ and intercept $a$, were calculated. Ideally, the measured and modeled exposures will agree across all pairs of $C_o$ and $C_p$, as indicated by a slope, $b$ equal to 1 and intercept, -$a$ equal to 0. Intercepts were evaluated using t-tests to determine if they were statistically significantly different from 0:

$$b=-\frac{{\sum }_{i=1}^n\left[\left(C_{oi}-{\overline{C}}_o\right)\left(C_{pi}-{\overline{C}}_p\right)\right]}{{\sum }_{i=1}^n\left[{\left(C_{oi}-{\overline{C}}_o\right)}^2\right]}$$ (4)

$$-a=\overline{C_p}-\left[b\times \overline{C_0}\right]$$ (5)

The degree of prediction error was quantified by the magnitude of the Normalized Mean Square Error, NMSE. When there is perfect concordance, the NMSE will equal 0. Higher values of NMSE indicate greater magnitudes of discordance between $C_o$ and $C_p$:

$$NMSE=\frac{{\left(\overline{C_p-C_o}\right)}^2}{\left[\left({\overline{C}}_o\right)\left({\overline{C}}_p\right)\right]}$$ (6)

Bias, assessed as the Normalized or Fractional Bias, FB, was calculated for each test as the mean bias of all $C_o-C_p$ pairs. The FB will ideally have a value of 0 when all pairs of $C_o$ and $C_p$ match. The degree to which they do not agree will be evident by the magnitude of departure of FB from zero:

$$FB=2\times \left[\frac{\overline{C_p}-\overline{C_o}}{\overline{C_p}+C_o}\right]$$ (7)

Performance criteria for this parameter is defined in the standard as ≤0.25.

Model performance was also evaluated categorically, using the Exposure Control Categories (ECC) defined in the AIHA Exposure Assessment Strategies framework (Table 4).^[14–16]

Table IV.

Framework showing AIHA Exposure Control Categories (ECC) and recommended statistical interpretation

AIHA Exposure Control Category (ECC)	Proposed Control Zone Description	General Description	AIHA-Recommended Statistical Interpretation
1	Highly Controlled (HC)	95th percentile of exposures rarely exceeds 10% of the OEL	X0.95 ≤ 0.10 OEL
2	Well Controlled (WC)	95th percentile of exposures rarely exceeds 50% of the OEL	0.10 OEL ≤ X0.95 ≤ 0.50 OEL
3	Controlled (C)	95th percentile of exposures rarely exceeds the OEL	0.50 OEL ≤ X0.95 ≤ OEL
4	Poorly Controlled (PC)	95th percentile of exposures exceeds the OEL	OEL ≤ X0.95

TWA exposures were calculated from the measured and modeled exposure data for each test. Thus, from each set of three replicate tests for each condition, two sets of exposure estimates were developed: one based on exposure measurement data and a parallel set of assessments derived from modeled exposure data. Test replicates of each scenario (set of conditions) were combined into a single Exposure Scenario (ES) for the categorical analysis so that each ES contained 3 replicate tests x 6 sample locations generating scenarios with n = 18 measurements. A total of 27 ESs were used to evaluate the WMR model performance categorically. For the NF–FF model, 27 ESs were assessed. The NF and FF data sets differed from the WMR ESs; since only one location in the NF was sampled, each NF ES contained 3 replicate tests x 1 location, producing n = 3 measurements. The FF ESs contained 3 replicate tests x 3 sample locations generating n = 9 measurements. The group 95th percentile for each ES was then calculated and compared against the selected Occupational Exposure Limit (OEL) to determine the ECC to which it belonged. Two types of OELs were used in the analysis, the Occupational Health and Safety Administration Time Weighted Average Permissible Exposure Limit (OSHA PEL-TWA) and the Action Limit (AL) defined as $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ the OSHA PEL. In some cases, companies use the AL instead of the PEL as the benchmark that drives exposure and risk management actions, so it was included along with the PEL in this analysis. The ECC to which the scenario belonged based on modeled exposures was then evaluated for concordance with the Reference ECC, defined as the ECC to which the ES belonged based on the measurement data alone. If they were the same, then categorical agreement was achieved. If the modeled ECC was one category higher than the Reference ECC, it was identified by +1, indicating it overestimated the correct ECC by 1 category.

Last, the predicted ECCs were used to evaluate the impact of using the wrong model, providing insight into how robust each model was. For example, to investigate model performance of the NF-FF model in predicting exposures occurring in a well-mixed room environment, the ECC corresponding to modeled NF was compared to the Reference ECC derived from measurements in the WMR tests.

Results

Model evaluation – WMR model

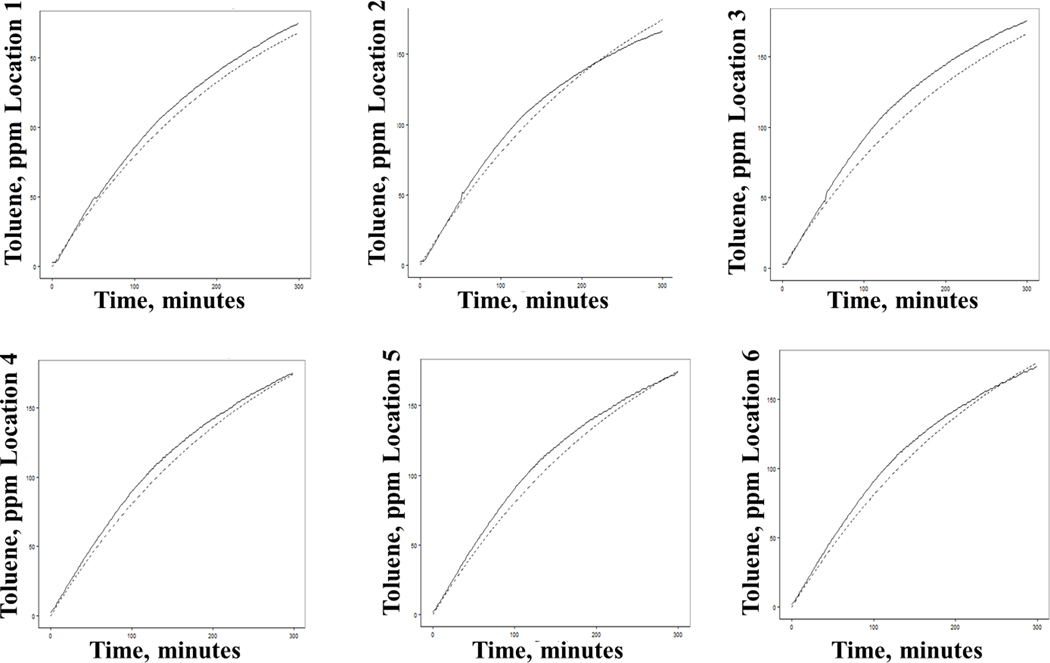
For each test and sampling location, a dataset of ${\text{C}}_{\text{measured}}$ values and a corresponding set of ${\text{C}}_{\text{modeled}}$ values were generated. For the WMR model evaluation, six pairs of ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ comparisons were generated from each test replicate. The similarity in ${\text{C}}_{\text{measured}}$ values across the six locations was consistent with a well-mixed environment (Figure 4 and Tables S1–S3 in the Supplemental Materials).

Figure 4.

Measured and modeled toluene concentrations for the WMR model, corresponding to the six sampling locations in the chamber from which the concentrations were measured when $\text{G}=43.2$ mg/min and $\text{Q}=0.05$ m³/min.

WMR model performance was evaluated in accordance with ASTM 5157 using 486 pairs of ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ exposures from three different solvents. Since samples were collected at 6 locations in the chamber in each of the toluene and acetone studies, 162 pairs were obtained. During one of the 2-butanone tests however, one of the MGM failed to collect the data, reducing the data recovered to 3 instead of 6 sampling locations. Consequently, the total number of 2-butanone pairs was 159. Results, showing the mean values calculated across all pairs and the percent for each chemical group, i.e., based on 162 pairs, falling within the acceptable ranges are presented in Table 5. A comparison of modeled versus measured concentrations generated from the low, medium, and high ventilation rates are presented in Figures 5 –5c. Results for each test showing emission and ventilation rates, mean measured and modeled concentrations and performance statistics are presented in the Supplemental Materials, Tables S1–S3. Specifically, for each test, six measured and modeled pairs were evaluated and their respective scores for each performance parameter recorded. For example, in test 1, six locations were sampled. Results are shown for the measured and modeled pair from location 1 as 1.1, and from location 2 as 1.2, etc.

Table V.

Evaluation of the WMR model using ASTM 5157 Criteria. Acceptable values or ranges are shown in parenthesis. NMSE: Normalized Mean Square Error; FB: Fractional Bias

WMR Model Performance Evaluation
ASTM 5157 Criteria	Results
Correlation coefficient, r (≥ 0.9)	Toluene	2 Butanone	Acetone
Mean	0.99	1	1
% acceptable	100%	100%	100%
slope, b (0.75 – 1.25)
Mean	1.01	−1.06	0.94
% acceptable	99%	88%	97%
intercept, a (≤ 25% C average)
Mean	0.47	−1.06	0.01
Intercept p-value	0.28	.18	0.98
% acceptable	100%	100%	100%
NMSE (≤ 0.25)
Mean	0.01	0.03	0.02
% acceptable	99%	100%	99%
FB (≤ 0.25)
Mean	0.06	0.13	0.02
% acceptable	97%	95%	99%
Acceptable (all criteria)	97%	88%	97%

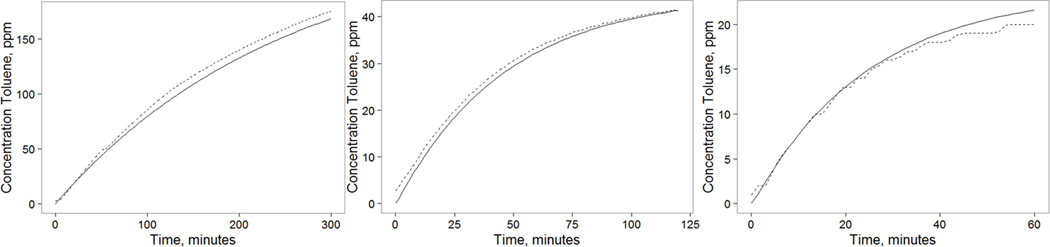
Figure 5.

(a)–(c): WMR Co (solid line) and Cp (dashed line) for Low Q, $\text{t}=300$ min (0.06 m³/min); (b): Medium Q, $\text{t}=120$ min (0.24 m³/min); (c): High Q, $\text{t}=60$ min (0.52 mg/m³).

Model performance was deemed adequate when all criteria were met, in accordance with ASTM 5157. The WMR model performance was adequate in 96% of the toluene tests, 88% in the 2-butanone tests and 97% of the acetone tests. The intercepts were not significantly different from zero. Since FB was calculated for ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ pairs recorded every 1.5 min for the duration of each study, temporal patterns of bias were also investigated for each set of replicate tests. In the case of FB, the greatest bias was observed, not surprisingly at the beginning of each test reflecting the less than instantaneous mixing in the chamber when the contaminant generation first started, resulting in ${\text{C}}_{\text{modeled}}>{\text{C}}_{\text{measured}}$. FB decreased as the tests progressed and as steady state conditions were approached (Figures S1a –c in Supplemental Materials).

Categorical accuracy was evaluated using two benchmarks, the OSHA PEL-TWA and the AL. The decision statistic upon which the ECC classification is based is the 95th percentile of the distribution of measured and modeled exposures, for each ES. Each ES comprised 18 measured or modeled exposure estimates, the concordance between the Reference and predicted ECCs for each these 27 SEGs evaluated. Using the PEL as the benchmark, the WMR model was categorically accurate for 26/27 scenarios. When the AL was used as the benchmark, the model was categorically accurate for all 27 scenarios. Results are presented in Table 6 which shows the number of categorically accurate tests by ECC, for each ES. For example, when the OSHA PEL was the benchmark OEL, for the tests using toluene, there was one scenario that was a Category 1 exposure. The WMR model correctly predicted a Category 1 exposure for that scenario and is reported as 1/1.

TABLE VI.

Categorical Evaluation of WMR Model applying the AIHA Exposure Category criteria and identifying the category to which the SEG’s 95^th percentile belongs. ECC: Exposure Control Category; PEL: OSHA Permissible Exposure Limit; AL: Action Limit

WMR Categorical Accuracy
	Toluene	2-Butanone	Acetone	Toluene	2-Butanone	Acetone
ECC	PEL = 200 ppm	PEL =200 ppm	PEL = 250 ppm	AL = 100 ppm	AL = 200 ppm	AL = 125 ppm
1	1/1	1/1	1/1
2	5/5	4/6	4/4	4/4	3/4	4/4
3	2/2	1/1	2/2	2/2	1/3	1/1
4	1/1	1/1	2/2	3/3	2/2	4/4
Total	9/9	7/9	9/9	9/9	6/9	9/9

Model evaluation — NF–FF model

Measured and modeled NF and measured and modeled FF pairs were compared to evaluate model performance. The NF-FF model was evaluated against the ASTM criteria using 81 pairs of NF and 243 pairs of FF exposures = 324 pairs of ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ exposures across three different solvents. Modeled NF and FF concentrations were higher than the measured concentrations. Performance criteria were met for the correlation coefficient, the slope, and NMSE for ≥67% of the NF pairs. However, since all criteria must be met for the model performance to be deemed adequate, the NF–FF Model (Near Field) performance was deemed adequate in only 33%, 19%, and 11% of tests for the 3 solvents. The NF–FF model (Far Field) performance was deemed adequate for 69%, 91%, and 97% of the tests for the 3 solvents. Results are presented in Table 7. Results for each test showing emission and ventilation rates, mean measured and modeled concentrations, and performance statistics are presented in the Supplemental Materials, Tables S4–S6.

Table VII.

Evaluation of the NF-FF model using ASTM 5157 Criteria. Acceptable values or ranges are shown in parentheses. NMSE: Normalized Mean Square Error; FB: Fractional Bias

NF-FF Model Performance Evaluation
ASTM 5157 Criteria	Solvent
	Toluene		2 Butanone		Acetone
Correlation coefficient, r (≥ 0.9)	NF	FF	NF	FF	NF	FF
Mean	0.95	0.99	0.91	0.91	0.93	0.91
% acceptable	81%	100%	67%	99%	99%	100%
Slope, b (0.75 – 1.25)
Mean	1.01	1.26	0.93	1.12	0.9	0.94
% acceptable	89%	69%	96%	91%	81%	97%
Intercept, a (≤ 25% C average)
Mean	25.1	3.39	33.8	−1.5	54.6	3.51
% acceptable	44%	100%	19%	98%	11%	100%
NMSE (≤ 0.25)
Mean	0.18	0.11	0.2	0.06	0.23	0.03
% acceptable	89%	99%	78%	94%	94%	96%
FB (≤ 0.25)
mean	0.36	0.24	0.35	0.01	0.42	−0.06
% acceptable	33%	75%	26%	93%	15%	100%
Acceptable (all criteria)	33%	69%	19%	91%	11%	96%

To categorically evaluate NF FF model performance, the OSHA PEL or ACGIH TLV and AL served as the benchmarks. The model predicted the correct ECC for 21/27 NF scenarios and 20/27 NF scenarios when benchmarked against the PEL and AL, respectively. These results were highly statistically significant ($\text{p}<0.001$). For Far Field exposures, the NF–FF model correctly predicted the ECC for 26/27 FF scenarios for both benchmarks. These results were also highly statistically significant ($\text{p}<0.001$). Categorical analysis of the NF FF (NF model) is presented in Table 8a by chemical and benchmark and for the FF categorical analysis, results are shown in Table 8b.

TABLE VIIIa.

Categorical Evaluation of NF-FF Model – Near Field; ECC: Exposure Control Category; PEL: OSHA Permissible Exposure Limit; AL: Action Limit; TLV: ACGIH TLV

NF-FF Categorical Accuracy – Near Field
	Toluene	2-Butanone	Acetone	Toluene	2-Butanone	Acetone
ECC	PEL = 200 ppm	PEL =200 ppm	TLV = 250 ppm	AL = 100 ppm	AL = 200 ppm	AL = 125 ppm
1
2	3/4	4/6	3/5	2/2	0/1	1/2
3	4/4	2/2	2/3	1/2	4/5	1/3
4	1/1	1/1	1/1	4/5	3/3	4/4
Total	8/9	7/9	6/9	7/9	7/9	6/9

TABLE VIIIb.

Categorical Evaluation of NF-FF Model – Far Field, ECC: Exposure Control Category; PEL: OSHA Permissible Exposure Limit; AL: Action Limit. TLV: ACGIH TLV

NF-FF Categorical Accuracy – Far Field
	Toluene	2-Butanone	Acetone	Toluene	2-Butanone	Acetone
ECC	PEL = 200 ppm	PEL =200 ppm	TLV = 250 ppm	AL = 100 ppm	AL = 200 ppm	AL = 125 ppm
1	1/1	1/1
2	6/6	6/6	6/6	4/4	4/4	2/2
3	1/2	2/2	3/3	3/3	3/3	3/4
4				2/2	2/2	3/3
Total	8/9	9/9	9/9	9/9	9/9	8/9

Last, the impact of model selection for a given set of chamber conditions was evaluated using the categorical data. In the first case, the NF-FF model was used to predict exposures occurring in a well-mixed environment. Specifically, the predicted NF 95th percentile concentration was compared to the measured 95th percentile WMR concentration (which is essentially equivalent to the FF concentration). The model overestimated exposures by up to 281% in 25/27 scenarios. Categorically, the model overestimated exposures by one to two ECCs and the magnitude with which the model overestimated exposure increased as the ventilation rate in the chamber increased. Scenarios reflecting less than well mixed environmental conditions for which the WMR model is used were also evaluated categorically. Measured NF exposures were compared to modeled FF exposures, using the 95th percentile estimate in both cases. The model underestimated exposures for 22/27 scenarios by as much as 71%. However, this numerical underestimation had varying impacts: 13/27 were still categorically accurate, while 8/27 exposures were underestimated by one ECC and 1/27 were underestimated by two ECCs.

Discussion

The experimental protocol included the use of two mixing fans to promote good mixing in the chamber and resulted in random air speeds ranging from 0.24–1.24 m³/min, which are consistent with air velocities measured in domestic residences.^[21] Thus, the fans provided a representative level of air movement, at least for residential environments. It is worth noting that the chamber tests were conducted without anyone present in the chamber. It is possible that a worker present in the NF could have an effect on the mixing and airflow, especially in the NF.

Two sets of criteria were applied to evaluate model performance in this study. The ASTM 5157 Standard provided a generic set of objective measures useful for gaining an overall sense of model concordance and potential bias which are important for understanding the bounds within which models are useful, as well as for comparing the performance of two or more models. This was especially useful because the WMR and NF–FF models have not been systematically evaluated until now and this general performance knowledge is important. More practically relevant to industrial hygiene is the categorical criterion applied to measure model performance. Since the type of exposure or risk management that occurs, if any, is highly influenced by the ECC to which the hygienist believes an exposure belongs, ensuring that the modeled exposure accurately predicts the correct ECC is critical to the model’s utility and value.

The WMR model performance using the ASTM 5157 criteria can be characterized as excellent, with ≥82% of the 483 pairs of ${\text{C}}_{\text{measured}}-{\text{C}}_{\text{modeled}}$ pairs deemed adequate. Categorically, the WMR model correctly predicted the correct ECC for 93% of the 27 scenarios. There were no observable trends associated with changing the generation or ventilation rates across the three solvents, suggesting the model is stable within the ranges of G and Q used in the study. The mechanism by which all three solvents become airborne is the same, i.e., evaporation, and hence despite having different vapor pressures with different propensities for volatilizing, the solvent did not significantly impact the results.

Evaluating model performance under highly controlled conditions likely favors stronger performance, given the ability to control environmental conditions, and measure all model inputs with a reasonable degree of accuracy and precision. Thus, these results probably represent the best case. They strongly suggest that when conditions are likely to meet the model’s fundamental assumptions, using the WMR model to guide decisions about the magnitude and acceptability of exposure will increase the likelihood of making accurate decisions.

Model performance of the NF–FF model, based on the ASTM standard was not as strong as for the WMR model, with only 11–33% of the ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ NF pairs deemed adequate. This seemingly poor performance is largely driven by the estimates of the intercept and to a lesser degree, the fractional bias (FB) values that were outside the acceptable ranges defined in ASTM Standard 5157. The non-zero intercepts may be attributable to the physical environment not matching the model assumption of two perfectly mixed boxes very well. The model is influenced by the very small NF volume thus predicting a very steep rise in the NF concentration. Since the air within the chamber tended more towards a well-mixed, rather than a two zone (NF and FF) environment, the rate at which the contaminant concentration actually increased was more gradual than predicted. This difference is most severe at the beginning of the test. These findings point to two limitations of this study: sizing the NF to create spatial differences in the magnitude of exposure to create two distinct well mixed boxes, and despite efforts to position mixing fans to minimize advection, on occasion the fan located just beyond the NF caused the mean air speed to be greater than zero. Model performance for the FF was stronger than the NF, with 163 of the 243 ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ FF pairs (67%) deemed adequate.

Categorically, model performance of the NF-FF model predicted the correct ECC for 20/27 NF (∼74%) scenarios and 26/27 FF scenarios (∼96%). The categorical differences in NF ECCs are probably attributable to chamber conditions that reflect a WMR environment rather than a NF–FF environment: modeled NF exposures consequently exceeded measured NF exposures. Despite the limitations associated with the chamber size in achieving the ideal air dispersion patterns, model performance results support the use of the NF–FF model for guiding professional judgment when assessing scenarios for which the NF–FF model’s fundamental assumptions are met.

When a model is selected that is based on assumptions that are inconsistent with environmental conditions, modeled exposure estimates may not agree with the true exposures. Selecting the wrong model may be less consequential when environmental conditions differ only modestly from a model’s assumptions. Indeed, in industrial hygiene, differences that do not result in categorical misclassification may be inconsequential. The impact of selecting the wrong models was investigated under two different sets of conditions. Using the NF model to predict exposures when the environment is well mixed resulted in the majority of modeled exposures overestimating the true exposures. In 18/27 cases these differences did not result in categorical misclassification, but in 8/27 scenarios exposures were overestimated by one category. In one scenario, the modeled exposure overestimated the true exposure by two exposure categories. Thus, using the NF model to predict exposures in well-mixed environments is likely to over-estimate the true exposure, leading to unnecessary follow-up activities 33% of the time. Using the WMR model to predict exposures occurring in a NF environment leads to more serious errors. The WMR model underestimated the true exposure for 22/27 scenarios, with differences between the measured and modeled exposure sufficiently large to cause categorical misclassification for 10/27 of the scenarios. In most cases, the model underestimated the true exposure by one category. There was one scenario for which the true exposure was underestimated by two categories. Thus, using the WMR model to assess NF–FF scenarios could result in insufficient follow up 33% of the time, based on the chamber study data. However, it is likely that the impact will be even greater in real-world environments, where there is more variability in environmental conditions and more model input uncertainty. Since this could lead to inappropriate decision making and follow-up, careful attention in selecting the right model for a given scenario and set of conditions is essential.

The greater investment required when using the more sophisticated models such as the NF–FF model reflects the lack of investment in developing sub-models to estimate model inputs such as beta witha reasonable degree of accuracy. Ideally, these sub-models would be based on inputs that could be readily measured or estimated reasonably accurately. Indeed, values for $\beta$ were estimated post hoc, using local air speed measurements collected concurrently with airborne concentration measurements so $\beta$ not a predicted value. Thus, this additional cost underscores a general research need that should not be construed as model weakness.

Conclusion

The WMR and NF–FF model performance, evaluated across more than 800 ${\text{C}}_{\text{measured}}$ and ${\text{C}}_{\text{modeled}}$ pairs support their use for estimating the magnitude and acceptability of occupational and non-occupational exposures to chemicals. However, the model selected must be based on assumptions that are likely to be consistent with the exposure scenario and for this, model selection and application guidance is needed. More research is needed to develop databases of model input values and scenarios for these models to be fully utilized and valued.