Abstract
The functional diversity of RNAs is encoded in their innate conformational heterogeneity. The combination of single-molecule spectroscopy and computational modeling offers new attractive opportunities to map structural transitions within nucleic acid ensembles. Here, we describe a framework to harmonize single-molecule Förster resonance energy transfer (FRET) measurements with molecular dynamics simulations and de novo structure prediction. Using either all-atom or implicit fluorophore modeling, we recreate FRET experiments in silico, visualize the underlying structural dynamics and quantify the reaction coordinates. Using multiple accessible-contact volumes as a post hoc scoring method for fragment assembly in Rosetta, we demonstrate that FRET can be used to filter a de novo RNA structure prediction ensemble by refuting models that are not compatible with in vitro FRET measurement. We benchmark our FRET-assisted modeling approach on double-labeled DNA strands and validate it against an intrinsically dynamic manganese(II)-binding riboswitch. We show that a FRET coordinate describing the assembly of a four-way junction allows our pipeline to recapitulate the global fold of the riboswitch displayed by the crystal structure. We conclude that computational fluorescence spectroscopy facilitates the interpretability of dynamic structural ensembles and improves the mechanistic understanding of nucleic acid interactions.
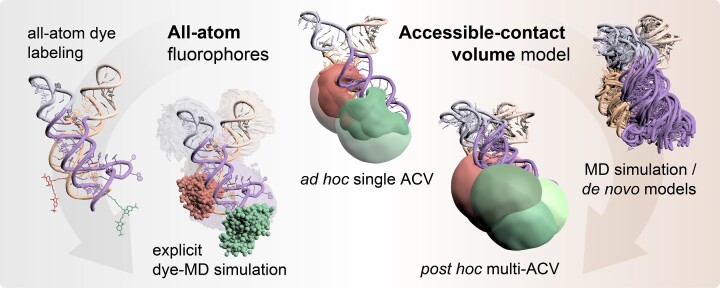
Graphical Abstract
Graphical Abstract.
Introduction
Structural dynamics are intrinsic to many biomolecules, defining transient structural states and empowering molecular function. Integrative structural modeling of nucleic acids and proteins has surged in recent years owing to an increasing availability of experimental restraints obtained by various biophysical techniques (1,2). Such restraints include electron density maps (3,4), chemical cross-links detected by quantitative mass spectrometry (5,6) and distances measured by electron paramagnetic resonance with pulsed electron–electron double resonance spectroscopy (7,8) or via Förster resonance energy transfer (FRET) (9–12). In combination with single-molecule detection, FRET lends itself to hybrid modeling as it can resolve short-lived conformational states (13–16) hidden in ensemble-averaged measurements. FRET is measured in solution and at low concentration, thereby avoiding macromolecular aggregation and crystal packing artifacts. With its high dynamic range, fluorescence spectroscopy therefore ideally complements the spatial resolution of crystallography, nuclear magnetic resonance (NMR) and cryo-electron microscopy (cryo-EM) (17–20).
Here, we leverage single-molecule FRET for integrated structural modeling of nucleic acids. Previous work in FRET-assisted modeling has focused predominantly on proteins (9–12,21). Nucleic acids and RNA pose particular challenges with respect to dye labeling (22) and intrinsic domain dynamics (23). With the ribose pucker and six torsion angles in the sugar–phosphate backbone, RNA molecules sample a vastly increased conformational space compared to proteins. Even small RNAs are rarely defined by a single structure but rather exist as a dynamic structural ensemble (23,24). The distribution of these conformers changes in response to protein binding (25–27), small-molecule interactions (28,29) or metal ion coordination (15,30). Depending on the size and complexity of the RNA, the structures resolved by experimental methods usually represent the most stable conformations. Molecular dynamics (MD) simulations address this limitation by computationally sampling trajectories, thereby filling the gaps between experimentally accessible structures (31).
Furthermore, de novo structure prediction has matured to a degree where energetically favorable structures can be computed directly from the nucleic acid sequence, hence bypassing laborious crystallization. Most approaches use fragments from libraries of annotated RNA motifs (32,33) to iteratively assemble complex architectures. Series of blind prediction challenges on various RNA structures have repeatedly ranked fragment assembly methods among the top scoring algorithms for RNA de novo modeling (34,35). These competitions have also highlighted that spatial restraints by chemical footprinting (36) or electron densities (3) help to guide and refine the predicted structures considerably. Incorporating dynamic information, such as FRET-based distance distributions, has remained challenging though (10,11,17,37).
To quantitatively connect the readouts of single-molecule FRET measurements to conformational changes, a dye model is required that maps the coordinates of the fluorescence emitters relative to the biomolecule. Here, we compare two modeling strategies, both designed to link FRET measurements with conformational ensembles. The first approach uses all-atom dyes that are covalently linked to the nucleic acid of interest, thus describing the dye dynamics as part of the MD simulation. While providing atomic level resolution, inclusion of explicit fluorophores is impractical, if not impossible in the case of de novo structure prediction. Therefore, we propose a post hoc calculation of the spatial fluorophore distribution for each timestep in an MD trajectory or for each candidate model in a de novo structural ensemble. This strategy builds upon our recently introduced implementation of the accessible-contact volume (ACV) in FRETraj (38). The ACV models the dye probe implicitly via a geometrical grid search and delineates the maximally accessible dye space given the spatial constraints imposed by the host biomolecule (9,39–41). FRET distributions are then derived from a time series or a de novo ensemble and validated against single-molecule FRET measurements.
Using a helical DNA fragment as a common and well-characterized FRET standard, we first illustrate how the molecular context is factored into ACV calculations. Herein, we characterize the influence of the relative ACV orientation, linker and dye dimensions as well as the accessibility of the labeled residues on the calculated FRET efficiency. This molecular-ruler-type cross-validation is complemented by a real-world use case where we model a structurally dynamic riboswitch de novo. We demonstrate the feasibility of including an experimentally derived FRET coordinate into model selection. Inclusion of a single experimental constraint rationally dissects the conformational space, filters out inconsistent conformers and results in a sub-ensemble of folded states compatible with FRET experiments.
Materials and methods
In silico pipelines for FRET-assisted structural modeling described herein are logically separated into three stages that involve (i) constructing a DNA/RNA starting structure or de novo ensemble, (ii) labeling the candidate model with dye probes and (iii) predicting FRET and/or dye anisotropy on a series of static structures or a short MD trajectory. Finally, the structural ensemble is validated against single-molecule FRET experiments.
Nucleic acid structure preparation
DNA double strands were prepared with canonical B-form parameters derived from fiber diffraction data (42) included in PyMOL. De novo models of the Mn2+ riboswitch aptamer were generated using the Fragment Assembly of RNA with Full Atom Refinement (FARFAR2) protocol (32), which is part of the Rosetta modeling suite. The RNA sequence and secondary structure annotation were provided as inputs (Supplementary Methods). The top 500 models (10% of all predicted structures) were ranked by Rosetta energy (33) and used for downstream labeling and FRET predictions.
In silico dye labeling
All-atom model
All-atom fluorophores were attached in silico to C5-amino-modified deoxythymidines on the DNA donor (T19, T23 and T31) and acceptor strand (T31) or to the phosphate at the 5′ ends of a two-stranded Mn2+ riboswitch construct using the PyMOL plugin FRETlabel (github.com/rna-fretools/fretlabel; Supplementary Figure S1). The plugin automates the task of fusing PDB structures of the dye, linker and nucleic acid of interest. It uses a library of pre-configured dye–linker constructs that reproduce the most common labeling chemistries for nucleic acids (Supplementary Table S1). Force field parameters of the dyes were taken from the AMBER-DYES package (43) and expanded to the nucleic acid linkers (Supplementary Methods and Supplementary Figure S2).
ACV model
Dye accessible contact volumes (ACVs) were computed using a grid search, based on Dijkstra’s algorithm (Supplementary Figure S3) (39,44), and implemented by the Python package FRETraj (github.com/rna-fretools/fretraj) (38). The AV is the unweighted accessible space that a bioconjugated fluorophore can explore. It is constructed within a rectangular grid spanned around the fluorophore attachment site. A grid node is assigned to the AV given that (i) the node does not clash with the biomolecule surface and (ii) the node is reachable within a distance Llinker by a walk on the grid starting at the attachment site.
In the ACV model, the AV is additionally divided into two separate subvolumes: the contact volume (CV) is defined as a rim around the biomolecule with a diameter dCV (set here to match the middle dye radius R2,dye; Supplementary Table S2), while the free volume (FV) is the complement volume equaling AV − CV. The CV accounts for the tendency of the dye to interact with the host biomolecule. The fractional occupancy of the CV (χCV) was calibrated by the ratio of residual and fundamental anisotropy:
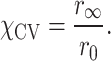 |
(1) |
By counting the number of grid nodes in the CV and the FV with weights ωCV and ωFV, respectively, we get
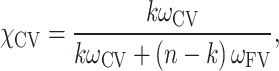 |
(2) |
where n is the total number of nodes and k is the number of nodes in the CV.
After rearrangement and defining 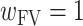 , each node in the CV was assigned a weight
, each node in the CV was assigned a weight
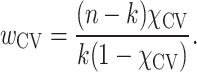 |
(3) |
FRET prediction
Transfer efficiencies between donor and acceptor fluorophores were calculated in two ways: (i) with all-atom dyes or (ii) from pairs of ACVs.
All-MD simulations
An inter-dye distance and a κ2 value were extracted for each frame of an MD trajectory (e.g. every picosecond). The time-dependent κ2(t) was computed from the orientation of the transition dipole vector of the donor and acceptor dye. The instantaneous (per frame) transfer efficiency E(t) was then calculated as
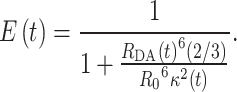 |
(4) |
Next, a time-averaged transfer efficiency 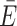 and associated standard deviation σE were calculated from a Markov process that simulates fluorescence emission events. This allowed us to compare the in silico FRET histograms directly against experimental distributions. The photons were sampled from a Markov chain defining the time-dependent transfer and fluorescence emission probabilities based on the dye distance RDA(t) (Figure 1, Supplementary Table S3 and Supplementary Methods). Each emitted photon was additionally annotated with a polarization (p = parallel, s = perpendicular) depending on the orientation of the fluorophore dipole.
and associated standard deviation σE were calculated from a Markov process that simulates fluorescence emission events. This allowed us to compare the in silico FRET histograms directly against experimental distributions. The photons were sampled from a Markov chain defining the time-dependent transfer and fluorescence emission probabilities based on the dye distance RDA(t) (Figure 1, Supplementary Table S3 and Supplementary Methods). Each emitted photon was additionally annotated with a polarization (p = parallel, s = perpendicular) depending on the orientation of the fluorophore dipole.
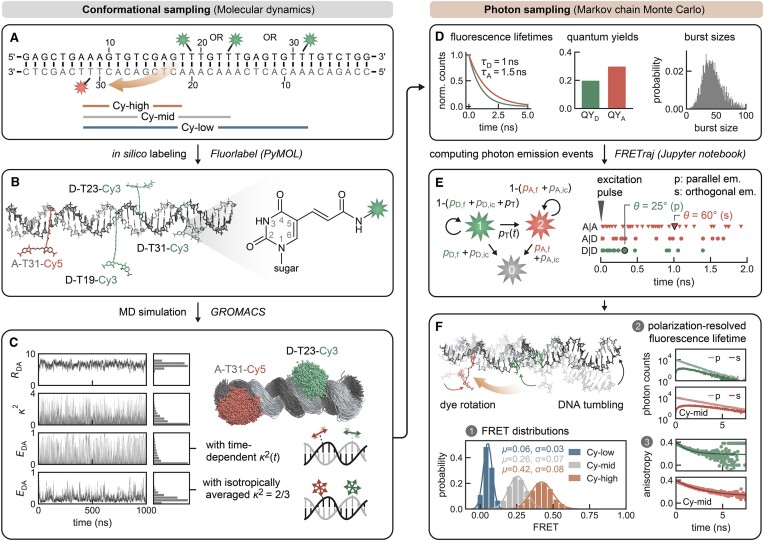
Figure 1.
Explicit all-atom fluorescence labeling enables in silico FRET prediction on a DNA molecular ruler (49). (A) The double-stranded DNA is labeled at residue T19, T23 or T31 with Cy3 and on the acceptor strand at T31 with Cy5. The FRET pairs are indicated as Cy-high (12 nt apart), Cy-mid (16 nt apart) and Cy-low (24 nt apart), respectively. (B) In silico labeling of the DNA helix via amino-modified deoxythymidines using the PyMOL plugin FRETlabel. (C) Structural ensemble from a 1 μs MD simulation showing point clouds of T23-Cy3 and T31-Cy5. Represented are the central carbon atoms of the polymethine chain of Cy3 and Cy5, respectively. The dye distance RDA, orientation factors κ2 and instantaneous FRET efficiency EDA (with either time-dependent κ2(t) and time-averaged κ2= 2/3) are monitored over the time course of the simulation. (D) Experimentally derived parameters (fluorescence lifetimes, quantum yields and burst sizes) define the relaxation rates in the Markov chain. (E) Donor and acceptor emission events after donor excitation (D|D and A|D) or by direct excitation of the acceptor (A|A) are simulated by Monte Carlo sampling and are assigned a polarization depending on the angle θ between the dye transition dipole at the time points of excitation and emission. (F) Shot-noise limited FRET distribution calculated by averaging over bursts from the 1 μs MD trajectory (all dynamics in the trajectory are fast compared to the burst duration; i.e. there are no slow conformational transitions). The polarization-resolved fluorescence lifetime and the derived dynamic anisotropy suggest some interactions of the dyes with the nucleic acid.
ACV simulations
In the second case, FRET is calculated from the distance between donor and acceptor ACVs. The position-averaged transfer efficiency 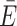 ACV of a single ACV pair is computed as
ACV of a single ACV pair is computed as
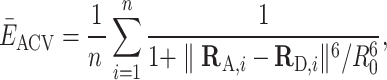 |
(5) |
where RD,i and RA,i are the coordinate vectors of 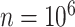 grid nodes sampled randomly from the donor and acceptor volumes while taking into account the respective weights of the grid points in either the CV or the FV (38,39,44). The uncertainty of the position-averaged FRET value scales with the size of the ACV and is estimated by the standard deviation of the bootstrap sample as
grid nodes sampled randomly from the donor and acceptor volumes while taking into account the respective weights of the grid points in either the CV or the FV (38,39,44). The uncertainty of the position-averaged FRET value scales with the size of the ACV and is estimated by the standard deviation of the bootstrap sample as
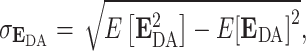 |
(6) |
where 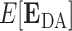 is the expected value of the transfer efficiency distribution computed by the dot product of the
is the expected value of the transfer efficiency distribution computed by the dot product of the 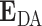 vector and the grid point weight vector
vector and the grid point weight vector 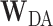 such that
such that 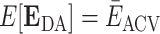 .
.
In multi-ACV trajectories, a new ACV was calculated every 100 ps. The time interval was chosen on the basis of the rotational correlation time of the dyes bound to DNA (τr,Cy3/5 = 1.1–1.5 ns; Supplementary Figure S4) and their fluorescence lifetime (τCy3/5 = 1.2–1.5 ns). Here, we computed about a dozen ACVs within the fluorescence lifetime, which is sufficient for subsequent sampling of photon events from the Markov chain (45,46). Similarly to the all-atom MD simulations, a time-averaged transfer efficiency 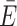 ACV and standard deviation σE,ACV were computed, with the only difference being the time-invariant orientation factor (κ2 = 2/3) since the dye orientation is conformationally averaged in the ACV.
ACV and standard deviation σE,ACV were computed, with the only difference being the time-invariant orientation factor (κ2 = 2/3) since the dye orientation is conformationally averaged in the ACV.
Multi-ACV benchmark and riboswitch model selection
The all-atom and multi-ACV-based FRET predictions were compared to fully corrected single-molecule FRET measurements. To this end, a thorough photophysical characterization of the donor and acceptor fluorophores was performed by measuring fluorescence lifetimes, quantum yields, dynamic anisotropies and burst sizes for the Cy3–Cy5 and Atto550–Atto647N pairs (Supplementary Figure S4). Gamma factors were determined from FRET stoichiometry (E–S) histograms (47). Computation of multi-ACVs along the MD trajectory reveals the bending flexibility of the nucleic acid on the timescale of the simulation (1 μs). The computed energy transfer distribution of EACV reflects the distance dynamics without additional broadening by shot noise.
Riboswitch models were selected by Rosetta energy and filtered by an experimentally informed FRET threshold. The best models were validated against the crystal structure by root mean square deviation (RMSD) and assessed by interaction network fidelity and deformation index (48) analogously to quality assessments in RNA puzzles. Additional details are given in the Supplementary Methods.
Results
All-atom dye simulations recapitulate single-molecule FRET distributions
MD simulations are a powerful companion approach to structurally interpret single-molecule FRET experiments. To calibrate our in silico FRET predictions, we first used a well-established FRET standard, a canonical DNA double helix. Specifically, we computationally and experimentally labeled a 38-nt double-stranded DNA at three distinct donor sites and a single acceptor position with sCy3 and sCy5 (Figure 1A and B). Three FRET distributions with low (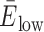 = 0.09 ± 0.06), intermediate (
= 0.09 ± 0.06), intermediate (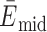 = 0.36 ± 0.16) and high transfer efficiencies (
= 0.36 ± 0.16) and high transfer efficiencies (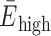 = 0.55 ± 0.14) were measured by confocal, single-molecule microscopy (Table 1, Supplementary Figure S4 and Supplementary Methods) (49). Next, we simulated 1 μs FRET-MD trajectories for each dye pair to obtain an ensemble of structures and dye positions (Figure 1C). This point cloud depicts the motion of both the DNA and the fluorophore. From the time-dependent inter-dye distance RDA(t) and orientation factor κ2(t), we derived instantaneous transfer efficiencies EDA(t). As this quantity is not accessible experimentally, we recalculated EDA(t) with a time-averaged κ2= 2/3. This reduces the noise in transfer efficiency distribution but does not yet account for dye photophysics. For a direct comparison to the single-molecule experiment, we therefore computed a series of photon bursts incorporating burst sizes, fluorescence lifetimes and dye quantum yields (Figure 1D and E). The resulting FRET histogram describes a shot-noise limited distribution with fast bending dynamics compared to the burst duration (Figure 1F). The computed anisotropy decays of sCy3 and sCy5 indicate weak sticking of the fluorophores to the DNA strands consistent with time-correlated single-photon counting (TCSPC) measurements (Figure 1F and Supplementary Figure S4) (41,50–52).
= 0.55 ± 0.14) were measured by confocal, single-molecule microscopy (Table 1, Supplementary Figure S4 and Supplementary Methods) (49). Next, we simulated 1 μs FRET-MD trajectories for each dye pair to obtain an ensemble of structures and dye positions (Figure 1C). This point cloud depicts the motion of both the DNA and the fluorophore. From the time-dependent inter-dye distance RDA(t) and orientation factor κ2(t), we derived instantaneous transfer efficiencies EDA(t). As this quantity is not accessible experimentally, we recalculated EDA(t) with a time-averaged κ2= 2/3. This reduces the noise in transfer efficiency distribution but does not yet account for dye photophysics. For a direct comparison to the single-molecule experiment, we therefore computed a series of photon bursts incorporating burst sizes, fluorescence lifetimes and dye quantum yields (Figure 1D and E). The resulting FRET histogram describes a shot-noise limited distribution with fast bending dynamics compared to the burst duration (Figure 1F). The computed anisotropy decays of sCy3 and sCy5 indicate weak sticking of the fluorophores to the DNA strands consistent with time-correlated single-photon counting (TCSPC) measurements (Figure 1F and Supplementary Figure S4) (41,50–52).
Table 1.
Comparison of experimental and computational FRET measurements
| Construct | Parameter | Single-molecule spectroscopya | All-atom MD simulationb | Single-ACV simulationc | Multi-ACV simulationd | Multi-laboratory benchmark studye |
|---|---|---|---|---|---|---|
| Cy-low: | R DA (Å) | 89 ± 8 | 87 ± 9 | 86 ± 10 (2) | 83.4 ± 2.5 | |
| T31(Cy3)–T31(Cy5) | E DA | 0.09 ± 0.06 | 0.06 ± 0.03 | 0.07 ± 0.05 | 0.06 ± 0.03 | |
| Cy-mid: | R DA (Å) | 66 ± 7 | 60 ± 9 | 60 ± 9 (2) | 60.3 ± 1.3 | |
| T23(Cy3)–T31(Cy5) | E DA | 0.36 ± 0.16 | 0.26 ± 0.07 | 0.39 ± 0.20 | 0.35 ± 0.07 | |
| Cy-high: | R DA (Å) | 58 ± 7 | 50 ± 10 | 49 ± 10 (1) | 51.7 ± 0.9 | |
| T19(Cy3)–T31(Cy5) | E DA | 0.55 ± 0.14 | 0.42 ± 0.08 | 0.60 ± 0.22 | 0.64 ± 0.08 |
a E DA in the single-molecule experiments is determined as the mean ± σ of a Gaussian mixture model.
b R DA in the all-atom MD is calculated as the mean ± σ of the inter-dye distance (central carbon atom of the polymethine chain) along the trajectory. EDA is computed from sampling photon events along the trajectory. σEDA is the standard deviation of the distribution after shot-noise broadening.
c R DA in single simulations is calculated by random sampling of distances from the donor and acceptor volumes considering the relative weights of the grid points and is given as mean ± σ. EDA is computed from Equation (5) and errors are propagated.
dThe multi-ACV RDA is a time average of all RDA computed along the trajectory. On average, the multi-ACV distances equal the single ACV corresponding to a straight double helix. The standard deviation of the dynamics is given in parentheses. Shot noise broadened EDA is computed by sampling photon events along the trajectory in analogy to all-atom MD.
e R DA calculated from experimental transfer efficiencies measured with Atto550–Atto647N in a multi-laboratory benchmark study (49). The comparison with our measured FRET efficiencies is given in Supplementary Table S4.
ACVs are a lightweight model for anisotropic dye distributions
All-atom MD simulations with fluorophores explicitly included in the force field are arguably the most faithful approach to model FRET experiments in silico (Figure 2A). However, the atomistic precision comes with a few significant constraints: First, explicit dyes and their linkers need to be parameterized a priori for the particular force field (see Supplementary Methods). Dye packages for the most common force fields and modeling suites have been published (43,53,54), but the list of available fluorophores and adaptors is nonexhaustive, thus often requiring manual modification of PDB structures and topologies. Second, each new dye position typically needs its own simulation. Only if all relevant labeling sites are known beforehand and the dyes are spaced sufficiently apart can multiple FRET pairs be run together in a single simulation. Depending on the size of the biomolecule of interest and the density of labeling sites, unwanted dye interference, however, often precludes such multiplexed simulations.
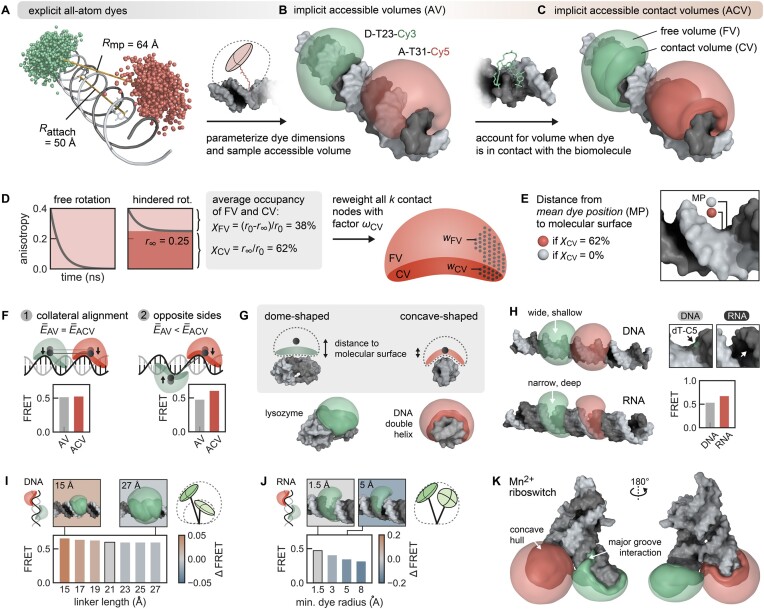
Figure 2.
The ACV represents an anisotropic dye model incorporating free and surface-interacting fluorophores. (A) Comparison of the distance Rattach and Rmp from explicit dye simulations on a DNA helix. Rattach is the distance between the attachment sites (here C5 of dT). Rmp represents the distance between the centers of the dye point clouds sampled in the MD simulation. Because the dyes are coupled to the biomolecule via flexible linkers pointing outward, it holds that Rattach < Rmp. (B) The dye point cloud is modeled by AVs after parameterizing the dye probe as an ellipsoid (9,39,41). (C) The ACV incorporates a rim around the DNA denoted as the CV, which is occupied when the dye sticks to the molecular surface. (D) Grid nodes in the CV are reweighted to account for the 62% occupancy of the CV as determined by time-resolved anisotropy (Equations 1–3). (E) The CV fraction χCV influences the mean dye position (sphere) in the volume. (F) The ACV orientation affects the predicted FRET efficiency 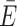 ACV only when ACVs are oriented in trans, i.e. on opposite sides of a poly-GC DNA helix (case 2). The Förster radius is set to R0 = 38 Å (Cy3–Cy7), thus yielding transfer efficiencies around 0.5 and maximizing sensitivity. Bootstrapped standard deviations of the single ACVs in all bar charts are omitted for clarity. (G) The biomolecular topology modulates both the ACV shape and the mean position of the dye. The low curvature of globular proteins like lysozyme (PDB: 2lzm) results in a dome-shaped ACV. On the contrary, the ACV wraps around double-stranded DNA with the concave shape shifting the mean position closer to the molecular surface. (H) The surface accessibility of the attachment site (here dT/U-C5) shapes the ACV and FRET prediction as a result of the different major groove dimensions of the B-form DNA and A-form RNA. (I) The linker length has little effect on the FRET value (the selected linker is outlined). (J) The smallest dye radius determines whether the fluorophore can intercalate in the groove and in return affect FRET. (K) The Mn2+ riboswitch (PDB: 6n2v) features a complex architecture where ACVs in P2 and P4 highlight potential interaction sites for the dyes in the major groove.
ACV only when ACVs are oriented in trans, i.e. on opposite sides of a poly-GC DNA helix (case 2). The Förster radius is set to R0 = 38 Å (Cy3–Cy7), thus yielding transfer efficiencies around 0.5 and maximizing sensitivity. Bootstrapped standard deviations of the single ACVs in all bar charts are omitted for clarity. (G) The biomolecular topology modulates both the ACV shape and the mean position of the dye. The low curvature of globular proteins like lysozyme (PDB: 2lzm) results in a dome-shaped ACV. On the contrary, the ACV wraps around double-stranded DNA with the concave shape shifting the mean position closer to the molecular surface. (H) The surface accessibility of the attachment site (here dT/U-C5) shapes the ACV and FRET prediction as a result of the different major groove dimensions of the B-form DNA and A-form RNA. (I) The linker length has little effect on the FRET value (the selected linker is outlined). (J) The smallest dye radius determines whether the fluorophore can intercalate in the groove and in return affect FRET. (K) The Mn2+ riboswitch (PDB: 6n2v) features a complex architecture where ACVs in P2 and P4 highlight potential interaction sites for the dyes in the major groove.
Post hoc dye models, which can be applied upon an existing MD simulation, are thus an attractive alternative to mitigate the shortcomings of all-atom simulations. Different models have been proposed to describe dye diffusion around an attachment site (9,39–41,55). As dyes tend to interact with the host molecule to different degrees, we have previously expanded the widely used AV model (Figure 2B) by treating the immediate environment around the biomolecule as a separate volume with higher weight (Figure 2C) (38,41). This reweighting of the AV by the dynamic anisotropy repositions the dye centroid closer to the biomolecule, which influences FRET under certain constellations (Figure 2D and E). In fact, the effect on FRET is expected to be maximal if the ACV clouds are positioned on opposite sides of the helix and minimal when aligned on the same side (collaterally). To quantify the change in FRET by the CV, we calculated donor and acceptor ACVs at different sites on a poly-GC DNA strand (Figure 2F). If the ACVs are on opposite sides of the helix (trans), inclusion of the CV increases the predicted mean FRET value by 0.13 FRET units (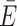 ACV = 0.61 ± 0.28 versus
ACV = 0.61 ± 0.28 versus 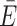 AV = 0.48 ± 0.26). However, if the ACVs are collaterally aligned (cis), the CV has little to no effect (
AV = 0.48 ± 0.26). However, if the ACVs are collaterally aligned (cis), the CV has little to no effect (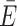 ACV = 0.54 ± 0.3 versus
ACV = 0.54 ± 0.3 versus 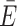 AV = 0.52 ± 0.28). On globular biomolecules such as many proteins, ACVs are usually facing away from each other; thus, the CV raises the calculated FRET value. This is consistent with the outcome of two independent FRET modeling campaigns targeting the proteins atlastin-1 and lysozyme, where the ACV model has shown to improve the accuracy of the predicted FRET values compared to the unweighted AV (9,14).
AV = 0.52 ± 0.28). On globular biomolecules such as many proteins, ACVs are usually facing away from each other; thus, the CV raises the calculated FRET value. This is consistent with the outcome of two independent FRET modeling campaigns targeting the proteins atlastin-1 and lysozyme, where the ACV model has shown to improve the accuracy of the predicted FRET values compared to the unweighted AV (9,14).
Not only the relative orientation but also the shape of the dye AV can affect FRET calculations. The form of the ACV depends on the topology of the biomolecule’s van der Waals surface. Globularly shaped proteins such as lysozyme, which are devoid of deep cavities, produce ACVs that appear as half domes (Figure 2G). Helical structures, on the other hand, lead to concave volumes as the ACV wraps around the spiraling stem. To further evaluate how the accessibility of the labeled residue determines the ACV and FRET, we compared a dT-C5 situated in the wide and shallow major groove of DNA to a U-C5 facing the narrow and deep major groove of RNA. The ACV around the heavily buried uridine in RNA contracts, leading to a shorter distance between the dyes and a higher FRET efficiency (Figure 2H).
Next, we asked whether intrinsic factors of the model, namely the length of the linker or the dye radius, have an impact on FRET. While the linker length barely affects the transfer efficiency (Figure 2I), increasing the smallest dye radius prevents the dye from intercalating in the groove and results in a lower FRET efficiency (Figure 2J). We conclude that both intrinsic parameters of the model such as the dye radius or the CV fraction and extrinsic factors (structural context) modulate FRET.
Folded RNA molecules often feature intertwined helices exposing cavities where fluorophores tend to get trapped. This is exemplified here by a metal-sensing riboswitch, labeled at the 5′ end and at an internal loop. The ACV is compressed between adjacent stem loops, increasing the fraction of CV nodes within the entire AV and reflecting the increased likelihood for dye–RNA interactions (Figure 2K). The degree of AV compaction and the relative contribution of the CV were shown to correlate with the extent of photoisomerization-related fluorescence enhancement (41,56,57). Surface interactions of dye and RNA are further enhanced by coordinated metal ions (41) as they bring together distant RNA domains to form tertiary contacts (46,52,58) like in the present Mn2+ riboswitch. Like with all-atom dye simulations, it is therefore recommended to visually inspect the resulting ACVs.
Multi-ACVs predict structural dynamics without explicit all-atom labeling
Having our post hoc dye model characterized in various structural contexts, we next asked whether the ACV model can fully substitute an all-atom FRET-MD simulation. To address this, we recalculated an ACV every 100 ps along an MD trajectory of the 38-nt DNA helix (Figure 3A and B). At each ACV timestep, a mean dye distance RDA was derived, monitoring DNA bending (59) on a sub-microsecond timescale. The bending angles show a positively skewed normal distribution with a maximum around 13°. Alignment of the DNA backbone produces coalescent volumes (multi-ACVs, Figure 3C) from which we extracted mean dye positions for each frame (Figure 3D). The resulting point cloud represents DNA dynamics, broadening the FRET distribution in the single-molecule experiment along with photon noise (Figure 3E). To incorporate the latter and to correct for quantum yield differences between the dyes, we again simulated photon emission events akin to all-atom dye simulations but with a time-invariant κ2= 2/3 (Figure 3F and G). The assumption of isotropic rotational averaging is justified by the observation that the mean κ2 in the explicit dye simulations indeed converges to precisely 0.66 (Supplementary Figure S5).
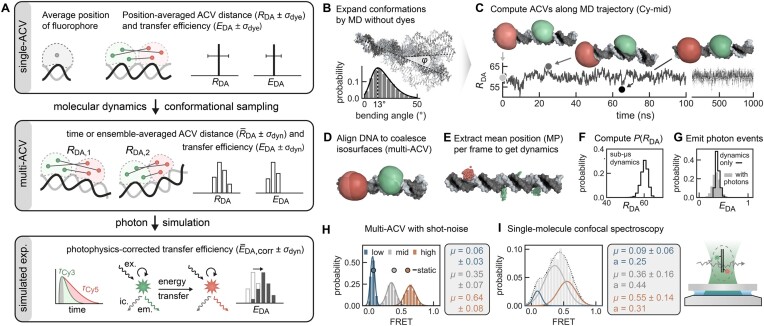
Figure 3.
Multi-ACVs simulate FRET-based conformational dynamics without the need of explicit dyes. (A) Schematic representation of distance metrics and their uncertainties in (multi)-ACV calculations. (B) Bending dynamics of the DNA FRET ruler are sampled by MD. (C) Serial ACVs are computed along the trajectory to define an RDA time trace with selected snapshots illustrating the bending motions of the DNA. (D) By aligning the DNA, the ACV isosurfaces coalesce (CVs were calculated but omitted for clarity in panels C and D). (E) Dye point clouds representing the mean position of the fluorophore are projected onto the idealized DNA helix. (E) Distribution of RDA distances sampled over the converged 1 μs MD trajectory. (F) Distances are converted to FRET efficiencies using Equation (5) (black line). (G) A Markov chain photon simulation (gray bars) accounts for additional broadening due to shot noise and dye quantum yields. (H, I) Comparison of the predicted FRET histograms from multi-ACV and single-molecule experiments. Single ACVs from ideal helices are indicated as spheres. The mean FRET efficiencies of the three subpopulations are recapitulated well by the simulations.
Next, we measured FRET distributions of the three cyanine dye pairs in equal stoichiometries by single-molecule confocal spectroscopy. The measurements were additionally cross-validated with a separate pair of rhodamine-derived Atto fluorophores, confirming the transfer efficiencies reported in a multi-laboratory benchmark study (Supplementary Figure S4B and Supplementary Table S4) (49). A comparison of the experiments with single- and multi-ACV calculations shows remarkable agreement of the FRET populations (Figure 3H and I, and Table 1). Deviations in the relative abundances are explained by varying dye labeling efficiency. We note that the all-atom dye simulation underestimates the transfer efficiency of the Cy-mid and Cy-high species. We attribute this to a disproportionate fraction of stacked versus free dye in the MD simulation, resulting from imperfections of the force field and its water model (41).
Altogether, we conclude that the ACV dye model is an appropriate alternative to a full-fledged, all-atom treatment of the fluorophores. ACV calculations provide an intuitive visualization of the dye positions on the biomolecule and help interpret abstract FRET coordinates especially when labeling sites are surface exposed. Buried attachment sites and nearby cavities pose some more challenges as they contract the ACV, consistent with the concept of photoisomerization-related fluorescence enhancement (57). We postulate that the implicit ACV model proves particularly useful in the following two scenarios: First, FRET predictions on a single structure can be performed very fast without running an MD simulation first. Second, multi-ACVs can effectively score hundreds of de novo modeled candidate structures using experimentally derived FRET restraints.
FRET selects de novo predictions of an intrinsically dynamic riboswitch
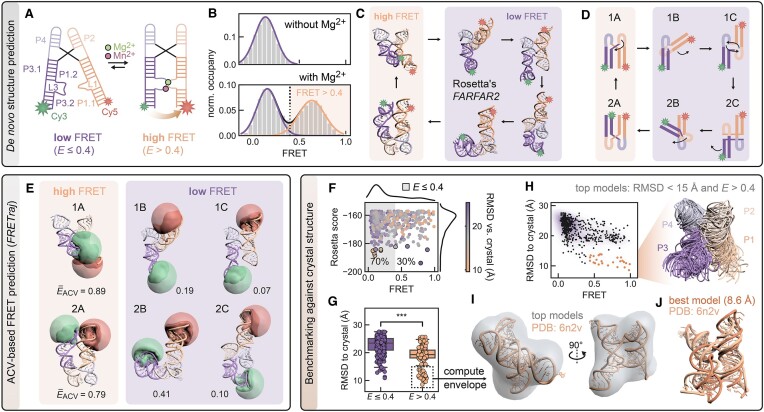
Recent RNA puzzle and CASP challenges have demonstrated that current RNA de novo prediction algorithms can generate models with remarkable similarity to crystal structures (34,35,60). Their scoring metrics still struggle though in predicting noncanonical base pairs and unambiguously ranking the top models. Orthogonal assessment methods, particularly measurements at a single-molecule level, may assist in model selection by invalidating structures that are inconsistent with experimental restraints. Here, we apply a single FRET coordinate to filter de novo modeled riboswitch aptamers consisting of two sets of coaxially stacked stem loops interconnected by a four-way junction (Figure 4A). We aim to reproduce the folded state of the riboswitch that is characterized by a mean transfer efficiency above 0.4 (Figure 4B) (20).
Figure 4.
A proof-of-principle FRET-assisted de novo modeling pipeline selects candidate structures of a dynamic Mn2+ riboswitch compatible with single-molecule FRET experiments. (A) Secondary structure of low and high FRET folding states of the riboswitch mediated by Mg2+ and Mn2+ binding. (B) FRET histogram illustrating the docking dynamics of the distal helical legs of the riboswitch leading to a high FRET population >0.4. Data from (20). (C) To predict the structure of the folded FRET state de novo, 5000 candidate models are generated by Rosetta from the nucleotide sequence (Supplementary Figure S6). (D) Schematic architectural configurations of the stem loops P1–P4 categorized by orientation (classes A, B and C) and coaxial stacking (type 1 and type 2; see the text). (E) The top 500 models (selected by their Rosetta energy score) encompass candidates of all orientation classes and stacking types. A donor and acceptor ACV is computed for each of these candidates. (F) Next, models were filtered by applying a FRET cutoff at E> 0.4, which reduces the fraction of candidate structures compatible with the folded riboswitch by 70%. (G) The ensemble of remaining models has a significantly lower mean RMSD to the crystal structure, suggesting that a single FRET coordinate can sort out ill-configured models while retaining native ones. (H) Selection of models with an RMSD < 15 Å to the crystal structure. (I) Overlay of the top models represented as ribbons. (J) Crystal structure aligned into the density map that is computed from the top models. Structural alignment of the best FRET-assisted de novo model to the crystal structure (RMSD = 8.6 Å).
We first predicted 5000 candidate structures from the nucleotide sequence and secondary structure annotations (Supplementary Figure S6A and B) using Rosetta’s FARFAR2 (32). Among the top 10% lowest energy models scored by FARFAR2’s energy function (Supplementary Methods), we found a variety of stem loop architectures that were broadly categorizable into three main classes: class A corresponds to models with slightly twisted but parallel oriented loops and class B represents structural intermediates where one of the helices is rotated by ∼90°, while class C includes fully flipped models with loops pointing in opposite directions. Interestingly, not only the orientation of the loops but also the coaxial stacking of the P1–P4 helices can be swapped. This leads to two sets of conformers (type 1 and type 2), each containing the three classes A, B and C and forming a conformational cycle (Figure 4C and D).
Next, we predicted FRET efficiencies for each of the 500 top candidates using the ACV dye model. Class A models showed the highest transfer efficiency with values above 0.4, consistent with the fraction of folded riboswitches in the single-molecule histograms, whereas class B and C models belong to the ensemble of unfolded or partially folded RNAs (Figure 4E). Using this FRET threshold, we filtered out 70% of the models leaving a subset of structures that on average have a lower RMSD to the crystallized conformer (Figure 4F and G). It is important to note that a single FRET constraint is not able to pinpoint a single candidate structure that would represent the native fold. In other words, our single FRET coordinate is unable to rank the remaining 30% of the models. However, candidates with highest similarity to the crystal structure are featured among them (Figure 4H). These models recapitulate the global topology of the riboswitch with its coaxially stacked and twisted helices as demonstrated by fitting the crystal structure into the envelope of the aligned structural ensemble (Figure 4I). The best model approximates the experimental structure with an RMSD of 8.6 Å after all-atom superimposition (Figure 4J). The metal-binding core with the noncanonical A-minor motif could not be fully reproduced, which is not unexpected given that divalent metal ions mediating core contacts are not considered in the FARFAR2 pipeline (Supplementary Figure S6C and D). Still, the overall interaction fidelity is reasonably high (INFall = 0.86, INFWC = 0.94, INFnWC= 0.8), suggesting that most Watson-Crick (WC) and the majority of non-WC contacts that are present in the crystal structure are also formed in the model. Some molecular dynamics are expected at the periphery with the stems of P1 and P3 being flexible to reorient, thus broadening the FRET histogram of the folded state in solution.
Discussion
FRET modeling has developed into a versatile tool to resolve short-lived structural ensembles (11,14,61–63). Here, we have described two complementary strategies to interface single-molecule FRET measurements with simulations of nucleic acids: the first uses explicit, all-atom fluorophores, while the second models dye dynamics implicitly by fluorescence dynamic anisotropy-weighted ACVs.
All-atom MD are considered the de facto gold standard for simulation of FRET experiments. Tracking the precise location of the fluorophore makes both translational and rotational dye components available to compute experimental properties, including fluorescence anisotropy. Knowledge about the inhomogeneity of a dye’s orientational distribution was also factored into the design of the ACV model. Through a linear combination of reweighted subvolumes delineating the accessible space of freely rotating and hindered dyes, we achieve more accurate FRET predictions than with the traditional AV model, consistent with previous results for proteins (9). Using helical DNA and RNA fragments as molecular rulers, we have identified both model intrinsic and contextual features of biomolecular environment that influence the sphericity of ACVs and FRET predictions. Multi-ACVs open up new avenues to design and perform in silico FRET screenings with various applications for de novo modeling, labeling site selection or post-processing of MD trajectories.
Compared to all-atom simulations, ACV screens are straightforward to set up, fast to run and simple to visualize and interpret. Being equally applicable to both single structures and ensembles, amenable to proteins and nucleic acids alike, the potential of multi-ACVs lies in the ability to make FRET coordinates and trajectories structurally explainable. For instance, ACV-based FRET predictions can rapidly inform about sensitive donor–acceptor sites to be followed up experimentally. Another key advantage of post hoc dye models is their applicability to existing or published datasets such as microsecond–millisecond long MD trajectories without predefined labeling sites. Important extrinsic factors that influence ACV-based FRET predictions include the accessibility of the labeling site and the presence of structural features such as grooves or stretches of exposed single-stranded nucleotides. Interactions of the fluorophores with these structural elements, visualized directly by all-atom MD and measured by photoisomerization-related fluorescence enhancement, are accounted for implicitly by reweighting of the CV. As opposed to atomistic simulations, the multi-ACV model does not track the exact fluorophore coordinates at any given time but integrates their dynamics over the simulation time. It is agnostic of fluorophore orientation and thus cannot be used to calculate anisotropy decays. Multi-ACV and all-atom MD simulations are thus complementary in many aspects and selecting one over the other depends on the specific use case (Table 2).
Table 2.
Comparison of all-atom fluorophores and the ACV model for FRET predictions
| All-atom fluorophores | ACVs | |
|---|---|---|
| FRET prediction type | MD simulation | Single PDB structure (crystal or cryo-EM structure) or structural ensemble (NMR, MD simulation, de novo models) |
| Dye position | Exact position of central dye atom at time t in trajectory | Average position of dye in sterically accessible volume for given structure |
| Computed distance | Exact distance between dye centers at time t in trajectory | Average distance between (multiple) ACVs for given structure or structural ensemble |
| Transition dipole | Yes | No |
| κ 2 | Time-resolved κ2(t) | Isotropic (κ2 = 2/3) |
| Readouts | Instantaneous transfer efficiency E(t) and time-resolved anisotropy r(t) | Mean transfer efficiency 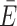 ACV ACV
|
| Dye labeling during | MD setup | Trajectory post-processing |
| Model | Dye/linker force field | Geometrical grid search |
| Implementation | FRETlabel | FRETraj |
| Photon sampling available (Markov process) | Yes (required) | Yes (optional) |
| Application scenarios | Reproducing single-molecule experiments in silico, including FRET, fluorescence lifetimes and anisotropy | Finding optimal FRET label positions, filtering de novo candidate models and selecting models that are consistent with FRET experiments |
| Computational expensesa | Fluorophore sampling (100–200 ns trajectory): hours to days depending on infrastructure | (Multi)-ACV calculation: seconds to minutes on personal computer |
aEstimated computational time for sampling the accessible space of the dye around the biomolecule relevant to the choice of the dye model. Time requirement for extensive conformational sampling of biomolecule is system dependent (size of biomolecule and the water box) and thus not specified here.
Finally, we have highlighted present and future challenges in FRET-assisted modeling. The de novo prediction of a metal-binding riboswitch nicely illustrates the quest for the proverbial hairpin in the haystack. Current state-of-the-art structure prediction workflows sample native-like folds among many suboptimal conformers. Validating true hits with high confidence is still a major difficulty though and prompts inclusion of complementary biophysical methods. Using FRET as a reaction coordinate in solution, we here dissected the modeled conformational ensemble of the riboswitch and were able to effectively narrow down the list of structural candidates by compatibility with the experimental constraints. However, a single FRET coordinate will not resolve the entire ensemble nor rank the most native-like models unambiguously. Instead, we demonstrated here the reuse of existing FRET data to augment de novo RNA modeling. It is encouraging though that among the models selected by the FRET filter we do find a subset of structures that aligns with subhelical accuracy to the crystal structure.
We envision that FRET as a low-dimensional but solution-based restraint with scalable time resolution will help to disentangle the dynamics of large RNAs and their networks, as it has for proteins (9,12,14). To this end, ACV-based screening is a convenient approach to figuring out which labeling sites to prioritize. Future studies will address how to include the most informative FRET coordinates as active restraints into integrative FRET modeling pipelines of nucleic acids, in order to not only select but also direct conformers along their folding route.
Supplementary Material
Acknowledgements
The authors thank Felix Erichson and Besim Fazliji for software testing and feedback.
Author contributions: F.D.S. and R.B. designed the research. F.D.S. performed and analyzed single-molecule measurements and MD simulations. R.A.C. ran MD simulations. R.K.O.S. and R.B. supervised the project. F.D.S. and R.B. wrote the manuscript with contributions from all authors.
Notes
Present address: Richard Börner, Laserinstitut Hochschule Mittweida, University of Applied Sciences Mittweida, Technikumplatz 17, Mittweida, Germany.
Contributor Information
Fabio D Steffen, Department of Chemistry, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland.
Richard A Cunha, Department of Chemistry, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland.
Roland K O Sigel, Department of Chemistry, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland.
Richard Börner, Department of Chemistry, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland.
Data availability
The source code of FRETraj (prediction of ACVs, https://doi.org/10.5281/zenodo.10898653), FRETlabel (labeling of nucleic acids with all-atom fluorophores, https://doi.org/10.5281/zenodo.10963145) and LifeFit (reconvolution-based fitting of eTCSPC data, https://doi.org/10.5281/zenodo.10966753) is available on GitHub (https://github.com/RNA-FRETools/) and Zenodo under the indicated DOIs. The PyMOL plugins are available as Docker containers with bundled open-source PyMOL. The packages are documented at https://rna-fretools.github.io/. The API of FRETraj is described in Jupyter notebooks with stepwise tutorials and examples. Protocols for dye–linker parameterization with FRETlabel are available at https://github.com/RNA-FRETools/fretlabel. De novo models of the manganese(II) riboswitch with accompanying Rosetta and FARFAR2 protocols are available on GitHub and Zenodo (https://doi.org/10.5281/zenodo.10963214 and https://doi.org/10.5281/zenodo.10963197). Additional source material is available from the corresponding author upon request.
Supplementary data
Supplementary Data are available at NAR online.
Funding
Swiss National Science Foundation [200020_165868 and 200020_192153 to R.K.O.S.]; University of Zurich (to R.K.O.S.); UZH Forschungskredit [FK-17-098 to F.D.S., FK-73521-10-01 to R.A.C., FK-14-096/15-095 to R.B.]. Funding for open access charge: Swiss National Science Foundation.
Conflict of interest statement. None declared.
References
- 1. Rout M.P., Sali A. Principles for integrative structural biology studies. Cell. 2019; 177:1384–1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bernetti M., Bussi G. Integrating experimental data with molecular simulations to investigate RNA structural dynamics. Curr. Opin. Struct. Biol. 2023; 78:102503. [DOI] [PubMed] [Google Scholar]
- 3. Kappel K., Zhang K., Su Z., Watkins A.M., Kladwang W., Li S., Pintilie G., Topkar V.V., Rangan R., Zheludev I.N. et al. Accelerated cryo-EM-guided determination of three-dimensional RNA-only structures. Nat. Methods. 2020; 17:699–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Malhotra S., Träger S., Dal Peraro M., Topf M. Modelling structures in cryo-EM maps. Curr. Opin. Struct. Biol. 2019; 58:105–114. [DOI] [PubMed] [Google Scholar]
- 5. Dorn G., Leitner A., Boudet J., Campagne S., Von Schroetter C., Moursy A., Aebersold R., Allain F.H.-T. Structural modeling of protein–RNA complexes using crosslinking of segmentally isotope-labeled RNA and MS/MS. Nat. Methods. 2017; 14:487–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Klykov O., Van Der Zwaan C., Heck A.J.R., Meijer A.B., Scheltema R.A. Missing regions within the molecular architecture of human fibrin clots structurally resolved by XL-MS and integrative structural modeling. Proc. Natl Acad. Sci. U.S.A. 2020; 117:1976–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Jeschke G. DEER distance measurements on proteins. Annu. Rev. Phys. Chem. 2012; 63:419–446. [DOI] [PubMed] [Google Scholar]
- 8. Peter M.F., Gebhardt C., Mächtel R., Muñoz G.G.M., Glaenzer J., Narducci A., Thomas G.H., Cordes T., Hagelueken G. Cross-validation of distance measurements in proteins by PELDOR/DEER and single-molecule FRET. Nat. Commun. 2022; 13:4396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Dimura M., Peulen T.O., Hanke C.A., Prakash A., Gohlke H., Seidel C.A. Quantitative FRET studies and integrative modeling unravel the structure and dynamics of biomolecular systems. Curr. Opin. Struct. Biol. 2016; 40:163–185. [DOI] [PubMed] [Google Scholar]
- 10. Dimura M., Peulen T.-O., Sanabria H., Rodnin D., Hemmen K., Hanke C.A., Seidel C.A.M., Gohlke H. Automated and optimally FRET-assisted structural modeling. Nat. Commun. 2020; 11:5394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Hellenkamp B., Wortmann P., Kandzia F., Zacharias M., Hugel T. Multidomain structure and correlated dynamics determined by self-consistent FRET networks. Nat. Methods. 2017; 14:174–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Agam G., Gebhardt C., Popara M., Mächtel R., Folz J., Ambrose B., Chamachi N., Chung S.Y., Craggs T.D., De Boer M. et al. Reliability and accuracy of single-molecule FRET studies for characterization of structural dynamics and distances in proteins. Nat. Methods. 2023; 20:523–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Zosel F., Mercadante D., Nettels D., Schuler B. A proline switch explains kinetic heterogeneity in a coupled folding and binding reaction. Nat. Commun. 2018; 9:3332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Sanabria H., Rodnin D., Hemmen K., Peulen T.-O., Felekyan S., Fleissner M.R., Dimura M., Koberling F., Kühnemuth R., Hubbell W. et al. Resolving dynamics and function of transient states in single enzyme molecules. Nat. Commun. 2020; 11:1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Panja S., Hua B., Zegarra D., Ha T., Woodson S.A. Metals induce transient folding and activation of the twister ribozyme. Nat. Chem. Biol. 2017; 13:1109–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Götz M., Barth A., Bohr S.S.-R., Börner R., Chen J., Cordes T., Erie D.A., Gebhardt C., Hadzic M.C.A.S., Hamilton G.L. et al. A blind benchmark of analysis tools to infer kinetic rate constants from single-molecule FRET trajectories. Nat. Commun. 2022; 13:5402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Lerner E., Barth A., Hendrix J., Ambrose B., Birkedal V., Blanchard S.C., Börner R., Sung Chung H., Cordes T., Craggs T.D. et al. FRET-based dynamic structural biology: challenges, perspectives and an appeal for open-science practices. eLife. 2021; 10:e60416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Borgia A., Borgia M.B., Bugge K., Kissling V.M., Heidarsson P.O., Fernandes C.B., Sottini A., Soranno A., Buholzer K.J., Nettels D. et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature. 2018; 555:61–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Holm M., Natchiar S.K., Rundlet E.J., Myasnikov A.G., Watson Z.L., Altman R.B., Wang H.-Y., Taunton J., Blanchard S.C. mRNA decoding in human is kinetically and structurally distinct from bacteria. Nature. 2023; 617:200–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Suddala K.C., Price I.R., Dandpat S.S., Janeček M., Kührová P., Šponer J., Banáš P., Ke A., Walter N.G. Local-to-global signal transduction at the core of a Mn2+ sensing riboswitch. Nat. Commun. 2019; 10:4304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Heidarsson P.O., Mercadante D., Sottini A., Nettels D., Borgia M.B., Borgia A., Kilic S., Fierz B., Best R.B., Schuler B. Release of linker histone from the nucleosome driven by polyelectrolyte competition with a disordered protein. Nat. Chem. 2022; 14:224–231. [DOI] [PubMed] [Google Scholar]
- 22. Steffen F.D., Börner R., Freisinger E., Sigel R.K.O. Stick, flick, click: dNA-guided fluorescent labeling of long RNA for single-molecule FRET. Chimia. 2019; 73:257. [DOI] [PubMed] [Google Scholar]
- 23. Shi H., Rangadurai A., Abou Assi H., Roy R., Case D.A., Herschlag D., Yesselman J.D., Al-Hashimi H.M. Rapid and accurate determination of atomistic RNA dynamic ensemble models using NMR and structure prediction. Nat. Commun. 2020; 11:5531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Ganser L.R., Kelly M.L., Herschlag D., Al-Hashimi H.M. The roles of structural dynamics in the cellular functions of RNAs. Nat. Rev. Mol. Cell Biol. 2019; 20:474–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Holmstrom E.D., Liu Z., Nettels D., Best R.B., Schuler B. Disordered RNA chaperones can enhance nucleic acid folding via local charge screening. Nat. Commun. 2019; 10:2453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Jarmoskaite I., Denny S.K., Vaidyanathan P.P., Becker W.R., Andreasson J.O.L., Layton C.J., Kappel K., Shivashankar V., Sreenivasan R., Das R. et al. A quantitative and predictive model for RNA binding by human Pumilio proteins. Mol. Cell. 2019; 74:966–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Chauvier A., Porta J.C., Deb I., Ellinger E., Meze K., Frank A.T., Ohi M.D., Walter N.G. Structural basis for control of bacterial RNA polymerase pausing by a riboswitch and its ligand. Nat. Struct. Mol. Biol. 2023; 30:902–913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Breaker R.R. Riboswitches and the RNA world. Cold Spring Harb. Perspect. Biol. 2012; 4:a003566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Manz C., Kobitski A.Y., Samanta A., Keller B.G., Jäschke A., Nienhaus G.U. Single-molecule FRET reveals the energy landscape of the full-length SAM-I riboswitch. Nat. Chem. Biol. 2017; 13:1172–1178. [DOI] [PubMed] [Google Scholar]
- 30. Freisinger E., Sigel R.K.O. From nucleotides to ribozymes—a comparison of their metal ion binding properties. Coord. Chem. Rev. 2007; 251:1834–1851. [Google Scholar]
- 31. Bock L.V., Gabrielli S., Kolář M.H., Grubmüller H. Simulation of complex biomolecular systems: the ribosome challenge. Annu. Rev. Biophys. 2023; 52:361–390. [DOI] [PubMed] [Google Scholar]
- 32. Watkins A.M., Rangan R., Das R. FARFAR2: improved de novo Rosetta prediction of complex global RNA folds. Structure. 2020; 28:963–976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Watkins A.M., Geniesse C., Kladwang W., Zakrevsky P., Jaeger L., Das R. Blind prediction of noncanonical RNA structure at atomic accuracy. Sci. Adv. 2018; 4:eaar5316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Miao Z., Adamiak R.W., Antczak M., Boniecki M.J., Bujnicki J., Chen S.-J., Cheng C.Y., Cheng Y., Chou F.-C., Das R. et al. RNA-Puzzles Round IV: 3D structure predictions of four ribozymes and two aptamers. RNA. 2020; 26:982–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Miao Z., Adamiak R.W., Antczak M., Batey R.T., Becka A.J., Biesiada M., Boniecki M.J., Bujnicki J.M., Chen S.-J., Cheng C.Y. et al. RNA-Puzzles Round III: 3D RNA structure prediction of five riboswitches and one ribozyme. RNA. 2017; 23:655–672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Cheng C.Y., Chou F.-C., Kladwang W., Tian S., Cordero P., Das R. Consistent global structures of complex RNA states through multidimensional chemical mapping. eLife. 2015; 4:e07600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Parks J.W., Kappel K., Das R., Stone M.D. Single-molecule FRET-Rosetta reveals RNA structural rearrangements during human telomerase catalysis. RNA. 2017; 23:175–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Steffen F.D., Sigel R.K.O., Börner R. FRETraj: integrating single-molecule spectroscopy with molecular dynamics. Bioinformatics. 2021; 37:3953–3955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Kalinin S., Peulen T., Sindbert S., Rothwell P.J., Berger S., Restle T., Goody R.S., Gohlke H., Seidel C.A.M. A toolkit and benchmark study for FRET-restrained high-precision structural modeling. Nat. Methods. 2012; 9:1218–1225. [DOI] [PubMed] [Google Scholar]
- 40. Muschielok A., Andrecka J., Jawhari A., Brückner F., Cramer P., Michaelis J. A nano-positioning system for macromolecular structural analysis. Nat. Methods. 2008; 5:965–971. [DOI] [PubMed] [Google Scholar]
- 41. Steffen F.D., Sigel R.K.O., Börner R. An atomistic view on carbocyanine photophysics in the realm of RNA. Phys. Chem. Chem. Phys. 2016; 18:29045–29055. [DOI] [PubMed] [Google Scholar]
- 42. Arnott S., Hukins D.W.L. Optimised parameters for A-DNA and B-DNA. Biochem. Biophys. Res. Commun. 1972; 47:1504–1509. [DOI] [PubMed] [Google Scholar]
- 43. Graen T., Hoefling M., Grubmüller H. AMBER-DYES: characterization of charge fluctuations and force field parameterization of fluorescent dyes for molecular dynamics simulations. J. Chem. Theory Comput. 2014; 10:5505–5512. [DOI] [PubMed] [Google Scholar]
- 44. Sindbert S., Kalinin S., Nguyen H., Kienzler A., Clima L., Bannwarth W., Appel B., Müller S., Seidel C.A.M. Accurate distance determination of nucleic acids via Förster resonance energy transfer: implications of dye linker length and rigidity. J. Am. Chem. Soc. 2011; 133:2463–2480. [DOI] [PubMed] [Google Scholar]
- 45. Hoefling M., Grubmüller H. In silico FRET from simulated dye dynamics. Comput. Phys. Commun. 2013; 184:841–852. [Google Scholar]
- 46. Hoefling M., Lima N., Haenni D., Seidel C.A.M., Schuler B., Grubmüller H. Structural heterogeneity and quantitative FRET efficiency distributions of polyprolines through a hybrid atomistic simulation and Monte Carlo approach. PLoS One. 2011; 6:e19791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Lee N.K., Kapanidis A.N., Wang Y., Michalet X., Mukhopadhyay J., Ebright R.H., Weiss S. Accurate FRET measurements within single diffusing biomolecules using alternating-laser excitation. Biophys. J. 2005; 88:2939–2953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Parisien M., Cruz J.A., Westhof É., Major F. New metrics for comparing and assessing discrepancies between RNA 3D structures and models. RNA. 2009; 15:1875–1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Hellenkamp B., Schmid S., Doroshenko O., Opanasyuk O., Kühnemuth R., Rezaei Adariani S., Ambrose B., Aznauryan M., Barth A., Birkedal V. et al. Precision and accuracy of single-molecule FRET measurements—a multi-laboratory benchmark study. Nat. Methods. 2018; 15:669–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Sanborn M.E., Connolly B.K., Gurunathan K., Levitus M. Fluorescence properties and photophysics of the sulfoindocyanine Cy3 linked covalently to DNA. J. Phys. Chem. B. 2007; 111:11064–11074. [DOI] [PubMed] [Google Scholar]
- 51. Schröder G.F., Alexiev U., Grubmüller H. Simulation of fluorescence anisotropy experiments: probing protein dynamics. Biophys. J. 2005; 89:3757–3770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Best R.B., Hofmann H., Nettels D., Schuler B. Quantitative interpretation of FRET experiments via molecular simulation: force field and validation. Biophys. J. 2015; 108:2721–2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Schepers B., Gohlke H. AMBER-DYES in AMBER: implementation of fluorophore and linker parameters into AmberTools. J. Chem. Phys. 2020; 152:221103. [DOI] [PubMed] [Google Scholar]
- 54. Shaw R.A., Johnston-Wood T., Ambrose B., Craggs T.D., Hill J.G. CHARMM-DYES: parameterization of fluorescent dyes for use with the CHARMM force field. J. Chem. Theory Comput. 2020; 16:7817–7824. [DOI] [PubMed] [Google Scholar]
- 55. Eilert T., Beckers M., Drechsler F., Michaelis J. Fast-NPS—a Markov chain Monte Carlo-based analysis tool to obtain structural information from single-molecule FRET measurements. Comput. Phys. Commun. 2017; 219:377–389. [Google Scholar]
- 56. Lerner E., Ploetz E., Hohlbein J., Cordes T., Weiss S. A quantitative theoretical framework for protein-induced fluorescence enhancement–Förster-type resonance energy transfer (PIFE-FRET). J. Phys. Chem. B. 2016; 120:6401–6410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Ploetz E., Ambrose B., Barth A., Börner R., Erichson F., Kapanidis A.N., Kim H.D., Levitus M., Lohman T.M., Mazumder A. et al. A new twist on PIFE: photoisomerisation-related fluorescence enhancement. Methods Appl. Fluoresc. 2024; 12:012001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Grotz K.K., Nueesch M.F., Holmstrom E.D., Heinz M., Stelzl L.S., Schuler B., Hummer G. Dispersion correction alleviates dye stacking of single-stranded DNA and RNA in simulations of single-molecule fluorescence experiments. J. Phys. Chem. B. 2018; 122:11626–11639. [DOI] [PubMed] [Google Scholar]
- 59. Basu A., Bobrovnikov D.G., Cieza B., Arcon J.P., Qureshi Z., Orozco M., Ha T. Deciphering the mechanical code of the genome and epigenome. Nat. Struct. Mol. Biol. 2022; 29:1178–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Das R., Kretsch R.C., Simpkin A., Mulvaney T., Pham P., Rangan R., Bu F., Keegan R., Topf M., Rigden D. et al. Assessment of three-dimensional RNA structure prediction in CASP15. Proteins. 2023; 91:1747–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Opanasyuk O., Barth A., Peulen T.-O., Felekyan S., Kalinin S., Sanabria H., Seidel C.A.M. Unraveling multi-state molecular dynamics in single-molecule FRET experiments. II. Quantitative analysis of multi-state kinetic networks. J. Chem. Phys. 2022; 157:031501. [DOI] [PubMed] [Google Scholar]
- 62. Dittrich J., Popara M., Kubiak J., Dimura M., Schepers B., Verma N., Schmitz B., Dollinger P., Kovacic F., Jaeger K.-E. et al. Resolution of maximum entropy method-derived posterior conformational ensembles of a flexible system probed by FRET and molecular dynamics simulations. J. Chem. Theory Comput. 2023; 19:2389–2409. [DOI] [PubMed] [Google Scholar]
- 63. Chowdhury A., Nettels D., Schuler B. Interaction dynamics of intrinsically disordered proteins from single-molecule spectroscopy. Annu. Rev. Biophys. 2023; 52:433–462. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The source code of FRETraj (prediction of ACVs, https://doi.org/10.5281/zenodo.10898653), FRETlabel (labeling of nucleic acids with all-atom fluorophores, https://doi.org/10.5281/zenodo.10963145) and LifeFit (reconvolution-based fitting of eTCSPC data, https://doi.org/10.5281/zenodo.10966753) is available on GitHub (https://github.com/RNA-FRETools/) and Zenodo under the indicated DOIs. The PyMOL plugins are available as Docker containers with bundled open-source PyMOL. The packages are documented at https://rna-fretools.github.io/. The API of FRETraj is described in Jupyter notebooks with stepwise tutorials and examples. Protocols for dye–linker parameterization with FRETlabel are available at https://github.com/RNA-FRETools/fretlabel. De novo models of the manganese(II) riboswitch with accompanying Rosetta and FARFAR2 protocols are available on GitHub and Zenodo (https://doi.org/10.5281/zenodo.10963214 and https://doi.org/10.5281/zenodo.10963197). Additional source material is available from the corresponding author upon request.