Optimization-Based Pairwise Interaction Point Process (O-PIPP): A Precise and Universal Retinal Mosaic Modeling Approach

Abstract

Purpose

A retinal mosaic, the spatial organization of a population of homotypic neurons, is thought to sample a specific visual feature into the feedforward visual pathway. The purpose of this study was to propose a universal modeling approach for precisely generating retinal mosaics and overcoming the limitations of previous models, especially in modeling abnormal mosaic patterns under disease conditions.

Methods

Here, we developed the optimization-based pairwise interaction point process (O-PIPP). It incorporates optimization techniques into previous simulation approaches, enabling directional control of the simulation process according to the user-designed optimization target. For the convenience of the community, we implemented the O-PIPP approach into a Python package and a website application.

Results

We showed that the O-PIPP can generate more precise neural spatial patterns of healthy and diseased mosaics compared to previous phenomenological approaches. Notably, through modeling the retinal neural circuitry with O-PIPP–simulated retinitis pigmentosa cone mosaics, we elucidated how the cone mosaic rearrangement impacted the information processing of ganglion cells.

Conclusions

The O-PIPP provides a precise and universal tool to simulate realistic mosaics, which could help to investigate the function of retinal mosaics in vision.

Retinal mosaics refer to the spatial arrangement of homotypic neurons, which tile the retinal surface to sample specific visual information^1–3 and vary significantly across cell types.⁴ Recent investigations have provided quantitative descriptions of the spatial properties of mosaics from wild-type,^4–6 mutant,⁷ and diseased^8,9 retinas. These cell-type–specific mosaics play crucial roles in their functions and establishing local retinal circuits.^10–13 In addition to experimental approaches, computational models can provide novel insights into the formation and function of retinal mosaics.²⁵ One major modeling approach aims to simulate the formation process of retinal mosaics and evaluate the impact of developmental mechanisms such as homotypic interactions, lateral migration, cell fate determination, and programmed cell death.¹⁴ Based on these, mechanistic models that mimic the dynamics of neural development have been proposed to facilitate a better understanding of retinal mosaics, primarily focusing on photoreceptors^15–17 and ganglion cells.^18–20 However, the mechanism-specific details of these mechanistic models limit their availability in different retinal mosaics. Another modeling approach focuses on the similarity between spatial patterns of the model and the realistic data, at the price of omitting biologically plausible mechanisms. These phenomenological models offer more simplicity and generality when reproducing multitype mosaics^21,22 and thus are often used to study the function of retinal mosaics, such as the anti-aligned intermosaic coordination of primate retinal receptive fields.^12,13 However, the stochasticity in these models leads to difficulty in precisely reproducing the characteristics of spatial patterns, especially the abnormal clustered mosaics that are common in disease retinas.^23,24 Therefore, we need a more precise and universal retinal mosaic modeling approach.

In this work, we present the optimization-based pairwise interaction point process (O-PIPP), which enables directional control of the simulation process according to the user-designed optimization target. Results indicate that the O-PIPP approach could simulate wild-type (WT) healthy retinal mosaics ranging from highly regular to near-random patterns with higher precision, as well as diseased retinal mosaics featuring cell-free areas and clusters. In addition, by developing a three-layer retinal network model, we demonstrated how abnormal cone mosaics alter the receptive fields (RFs) of ganglion cells (GCs) in retinitis pigmentosa (RP), retinal dystrophies caused by photoreceptor loss. Overall, the O-PIPP provides an option for more precise and general mosaic modeling. Through the O-PIPP, we can quickly model many mosaic patterns that are consistent with the spatial characteristics of real retinal mosaic patterns observed in experiments. This allows researchers to use computational modeling to study the impact of these mosaic patterns on visual information processing in both healthy and diseased states.

Materials and Methods

In this section, we first introduce datasets of retinal mosaics for experiments. We then introduce the metrics of spatial patterns for mosaics and describe the technical details of the O-PIPP approach and the building of the three-layer network models. Finally, we provide the implemental details of this work. In Table 1, we list abbreviations and acronyms used in this article.

Table 1.

List of Abbreviations and Acronyms

Abbreviation	Definition	Abbreviation	Definition
AC	Amacrine cell	PIPP	Pairwise interaction point process
BC	(Retinal) bipolar cell	RF	Receptive field
CI	Convexity index	RI	Regularity index
GC	(Retinal) ganglion cell	RP	Retinitis pigmentosa
KL	Kullback–Leibler	SA	Simulated annealing
NN	Nearest neighbor	VD	Voronoi domain
NNRI	Nearest neighbor regularity index	VDRI	Voronoi domain regularity index
O-PIPP	Optimization-based pairwise interaction point process	WT	Wild-type

Datasets

This work used seven mosaics from WT retinas and rearranged cone mosaics from RP rat retinas. The side length (size) of these mosaic areas ranged from 100 µm to 500 µm, and the cell numbers (n) ranged from 80 to 850. Notably, due to the need to measure the spatial pattern of a single mosaic with statistical methods, we ignored the data of retinal mosaics with n < 50 to avoid inaccurate analysis results. We provide the mosaic-related spatial analysis results in Table 2.

Table 2.

Statistical Descriptions of WT Retinal Mosaics Across Cell Types

Cell Type	Size (µm)	N	NNRI	VDRI
Horizontal cell	300	87	4.512	4.357
Cholinergic AC	300	122	3.931	3.454
VGluT3 AC	300	98	3.406	3.036
AII AC	200	160	3.016	2.643
Type 2 BC	200	174	2.913	2.294
Type 3b BC	200	202	2.781	2.118
Type 4 BC	200	100	2.461	2.123
WT cone	491	850	4.120	3.493
RP cone	491	850	2.485	1.065

Multitype Mosaics From WT Mouse Retinas

The WT mouse retinal mosaics came from a published dataset⁴ including eight cell types: one horizontal cell (not distinguishing subtypes); four subtypes of amacrine cells (ACs), including cholinergic ACs, VGluT3 ACs, dopaminergic ACs, and AII ACs; and three subtypes of bipolar cells (BCs), including type 2 BCs, type 3b BCs, and type 4 BCs. For each cell type, the dataset contained an example natural mosaic with 20 to ∼250 cells in a square, and the spatial analysis resulted from 20 to ∼30 natural mosaics (Table 2). In this study, we ignored the data of dopaminergic ACs for their small n = 24.

Cone Mosaics From WT and RP Rat Retinas

Another published dataset⁹ provided the rat cone mosaics of WT and S334ter-line-3, a transgenic RP model. In this work, we used the rearranged RP cone mosaics at postnatal day 87 (P87; 6-week survival period), whose M-cones are highly clustered, and the data of WT cone mosaics on the same postnatal day. The mosaic rearrangement did not change the density of cones (∼4000 cells/mm²), so the WT cone mosaic and the RP one shared the same side length (size = 461 µm) and cell number (n = 850).

Metrics of Mosaic Spatial Patterns

In this study, we used the mouse horizontal cell mosaic as an example (Supplementary Fig. S1A) to introduce the metrics of spatial patterns.⁴ The first step of the analysis was Delaunay triangulation²⁵ to estimate neighborhoods based on cell positions (Supplementary Fig. S1B). Then, we calculated the nearest neighbor (NN) distance for the cell, the minimum distance to its neighbors (Supplementary Fig. S1C[1]). The triangulation also yielded a Voronoi diagram, and from that we could calculate the area of cell Voronoi domains (VDs; Supplementary Fig. S1C[2]). The frequencies of NN distances and VD areas represented special patterns of a mosaic (Supplementary Fig. S1D). We excluded cells close to the edges to avoid the boundary effect²⁶ and used transparent colors to label them in mosaic figures. After getting values of NN distances and VD areas, we could estimate the nearest neighbor regularity index (NNRI) and the Voronoi domain regularity index (VDRI). Here, the regularity index (RI) is the ratio between the mean value and the standard deviation of values, and NNRI is the mean of NN distances divided by the standard deviation. The VDRI follows the same calculation while using values of VD areas.

O-PIPP Approach

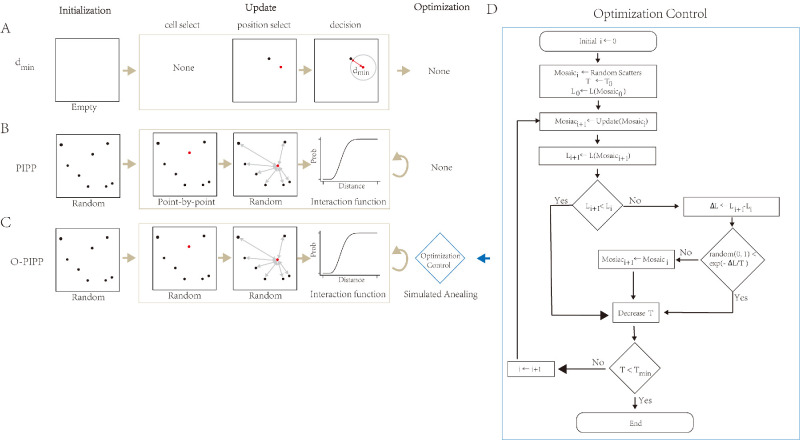
In this work, we summarized phenomenological modeling approaches into a three-stage process, including initialization, update, and optimization (Fig. 1). Two existing phenomenological models, the d_min model (Fig. 1A) and the pairwise interaction point process (PIPP) model (Fig. 1B), for comparison, are described in Supplementary Text S1.

Figure 1.

The “initialization–update–optimization” schema summarizes related phenomenological models and the O-PIPP approach. (A) The d_min model from Reference 21. This model begins at an empty area and inserts cells one by one until all insertions are finished. A new position is examined by the “exclusion zone” rule, and its distance to the closest neighbor must be larger than the d_min variable; otherwise, the model must find another position to satisfy the rule. (B) The PIPP model from Reference 22. This model begins at a random spatial distribution and uses a “death-and-birth” step to update all cells with a specific number of iteration steps. A selected cell is removed and reinserted into the mosaic with a new position. The selection of a position is a random process controlled by the distance-based interaction function, which forms the “exclusion zone” of cells. The PIPP model accepts all update iterations. (C) The O-PIPP approach in this work. This model incorporates simulated annealing techniques after an update to strategically accept the iteration results. (D) Schematic of the SA optimization in the O-PIPP approach.

In the O-PIPP, all of the cells start with random positions in the initialization stage, similar to the PIPP model. Then, the O-PIPP selects a certain proportion of cells and updates their positions simultaneously. Whether to accept this position update depends on whether the result of this update could make the modeling mosaic pattern closer to the mosaic pattern to be simulated. We used optimization algorithms (specifically, simulated annealing in this paper) to complete this decision-making process.²⁷ This was the reason why we named it O-PIPP. The optimization algorithm is a crucial part of the O-PIPP, not only controlling the optimization direction of the mosaic but also determining the termination conditions of the O-PIPP. In the following sections, we provide a more detailed description of the optimization process adopted in this paper.

Optimization Target

We used loss L to quantify the difference between the simulated mosaic and the realistic mosaic. We set L as the optimization target; therefore, the optimization algorithm would seek a mosaic with the smallest loss value. Based on the spatial pattern metrics in the Metrics of Mosaic Spatial Patterns section (Supplementary Fig. S1D), we defined a feature-based loss, L_F, of a simulated mosaic by summing up its Kullback–Leibler (KL) divergences of NN and VD²⁸ to the simulation target as

$$\begin{array}{c}\hfill L_F=\sum _i{p}_{NN}^s\left(i\right)*\log \left(\frac{p_{NN}^s\left(i\right)}{p_{NN}^t\left(i\right)}\right)+\sum _i{p}_{VD}^s\left(i\right)*\log \left(\frac{p_{VD}^s\left(i\right)}{p_{VD}^t\left(i\right)}\right)\end{array}$$ (1)

Here, i represents the histogram bin index of distribution, and p denotes the probability distribution of spatial features (subscript NN or VD) from mosaics (superscript s for simulated mosaic or t for target mosaic).

Optimization Process

In the O-PIPP, we used the simulated annealing (SA) algorithm to control the optimization process.²⁷ Here, we would like to use the symbols in SA but introduce their general meanings. We used T to represent the state of the optimization process, and its initial value was T₀. In each optimization, the O-PIPP calculated the loss of the newly generated mosaic, L_i+1 and compared it with the loss of the previous one (L_i). The O-PIPP would either accept the new mosaic if L_i+1 < L_i or accept the mosaic with a certain probability if L_i+1 > L_i. The acceptance probability, P_ac, was given as

$$\begin{array}{c}\hfill P_{ac}=e^{-\frac{L_{i+1}>L_i}{T_i}}\end{array}$$ (2)

where e denotes the exponential function, and T_i denotes the current state of the optimization process. After this, the O-PIPP would update the value of T strategically, as

$$T_{i+1}=\left\{\begin{array}{cc}\hfill T_i,& \hfill {\left[L\right]}_{i+1}\le {\left[L\right]}_i\\ \hfill \alpha *T_i,& \hfill {\left[L\right]}_{i+1}>{\left[L\right]}_i\end{array}\right.$$ (3)

where α is the hyperparameter to control the speed of optimization, and [L]_i denotes the average value of the loss of generated mosaics before.²⁹ As α < 1, the acceptance of a new mosaic would become more and more strict. The optimization process would be terminated when T was below a preset threshold (T_min).

For better clarification, we have visualized the trace of L_F alongside an O-PIPP optimization process on simulating the horizontal cell mosaic (Supplementary Fig. S2). The L_F was 1.21 at the beginning, and the corresponding distributions of features were obviously different from the target mosaic (inset 1 in Supplementary Fig. S2). After optimization, the L_F decreased to 0.08, and the corresponding feature distributions of the simulated mosaic were much closer to targets (inset 4 in Supplementary Fig. S2).

Parameters of the O-PIPP Model

Parameters of the O-PIPP model (Table 3) influenced the simulation in two stages:

• 1.During the cell update stage, parameters included those inherited from the PIPP (δ, ϕ, and α_h)³⁰ and the probability of update of a single cell, denoted as P_u, which was a specific parameter introduced in the O-PIPP. We maintained the values of δ, ϕ, and α_h as those used by the PIPP model and set the P_u as 0.01 after conducting a parameter search (refer to Supplementary Text S1, Section S3). Here, we chose to update only a portion of cell positions (P_u = 0.01) rather than updating all cell positions (P_u = 1) as in the PIPP. This decision ensures a smooth decrease in loss during the optimization process and enhances optimization efficiency.
• 2.During the optimization stage, parameters were mainly utilized to control the optimization process. These parameters included the initial state T₀, α for state updating, and termination threshold T_min. In our study, we applied the general parameter set (α = 0.95, T₀ = 2, T_min = 0.0001) on simulating the horizontal, AC, and BC mosaics. However, for cone mosaics, utilizing this set led to excessively long simulation times (>500,000 iterations). Instead, we chose a smaller value of T₀ (0.5), resulting in acceptable iteration numbers (100,000∼200,000). The chosen parameter values are listed in Table 3.

Table 3.

Parameters Employed in Models Across Cell Types

	O-PIPP				PIPP			d min
Cell Type	T 0	T min	α	Pu	δ	ϕ	αh	d mean	d std
Horizontal cell	2	0.0001	0.95	0.01	7.5	32.12	2.65	39	7
Cholinergic AC					5.0	33.02	3.01	39	8
VGluT3 AC					8.0	26.77	1.35	26	6
AII AC					1.5	10.02	1.35	7	2
Type 2 BC					2.0	7.04	1.96	7	2
Type 3b BC					2.0	8.33	2.72	7	2
Type 4 BC					1.5	13.84	1.10	5	1
WT cone	0.5				5.0	4.63	1.39	—	—
RP cone					4.0	2.03	5.22	—	—

In Supplementary Text S1, Section S3, we took the horizontal cell mosaic as an example to explore how parameter sets changed the performance of the O-PIPP model, and results indicated that the current choice (α = 0.95, T₀ = 0.5, T_min = 0.0001, and P_u = 0.01) was better than other parameters considering both the performance and the time consumption (Supplementary Figs. S3, S4). Parameters effects on d_min and the PIPP are shown in Supplementary Table S1 and Supplementary Figure S5, respectively.

Retinal Discrete Neuronal Network Models

In this section, we introduce how to build cone ON-type BCs and ON-type GC neuronal network models for WT and RP rat retinas with natural or simulated mosaics (Supplementary Fig. S6). The neural dynamics of the model³¹ and estimation of receptive fields^32,33 are described in Supplementary Text S2.

Neural Connections

Neural connections are restricted by the relative position and the radius of the dendrite field of cells. We adopted the following biologically plausible rules to constrain the connections of a single cell:

• 1.A cone inputs to a single BC or not.³¹
• 2.A BC receives a maximum of eight cone inputs.³⁴
• 3.A cell only receives inputs from cells with a distance less than its dendrite field radius (30 µm for BCs and 150 µm for GCs).³⁵
• 4.The BC that does not receive cone inputs is removed to mimic the dendritic retraction in the RP retina.³⁶

Cell Mosaics

The cone layer used generated mosaics or mosaics from the dataset provided earlier in the Cone Mosaics from WT and RP Rat Retinas section. The GC layer had only one cell with a random position. We used the O-PIPP approach to generate the WT BC mosaic. The RP circuitry models share the same BC mosaic due to the no-modification of the spatial organization of cone BCs at P87.³⁶ Due to the lack of data on cone bipolar cell spatial distribution, we designed a new optimization target, the connection-based loss, L_c. Specifically, after the update iteration, we built a network model with the generated BC mosaic and the WT cone mosaic by connecting rules discussed in the Neural Connections section. Then, we summarized connection pairs between BCs and cones and calculated loss L_c as

$$L_c=\left(1-\frac{B{C}_f}{N_{BC}}\right)+\left(1-\frac{C_f}{N_C}\right)$$ (4)

where BC_f and C_f denote the number of BCs and cones meeting these rules: A BC receives four to approximately six cone inputs,³⁴ and a cone has its downstream BC.³¹ N_cone = 850 and N_BC = 850/5 = 170 denote cell numbers, respectively.

Simulation Details

Due to the stochasticity in every model, we simulated 50 mosaics and calculated the average performance of mosaics as the final measurement. The parameters of the models are summarized in Table 3. We implemented all methods and computer simulations in Python with scientific computing packages (Numpy/Scipy/NetworkX), except that the interaction function parameters were estimated using R with the spatstat package (R Foundation for Statistical Computing, Vienna, Austria).³⁷ We have developed the O-PIPP package, written in Python 3, which is freely available from Github (https://github.com/heliy/OPIPP). With implemented simulation and optimization methods, it can generate mosaics with user-designed spatial features. We also provided a web application where users can upload retinal mosaics, do O-PIPP simulation, and download generated mosaics (https://opipp-online.streamlit.app/).

Results

We evaluated and compared modeling performance between the O-PIPP approach and previous models on different retinal spatial mosaic types (Fig. 2). After that, we demonstrated the specific ability of O-PIPP to model abnormal mosaics by modeling the clustered cone mosaic pattern from RP retinas (Fig. 3). Based on this, we built three-layer discrete neuronal network models with realistic RP cone mosaics and reproduced the RF alteration of GCs observed in experimental research (Fig. 4). Our results indicate the superiority of the O-PIPP approach in building more biologically realistic models.

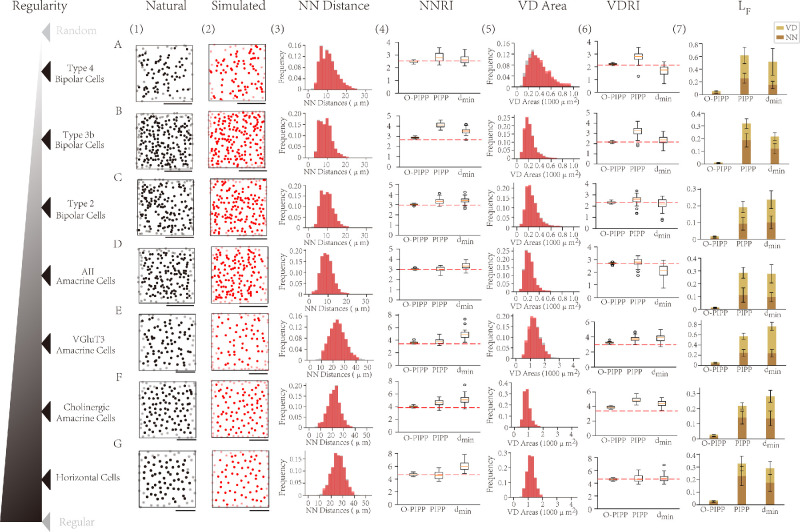
Figure 2.

Simulation results with the O-PIPP approach on WT retinal mosaics. (A–G) Cell types are ordered by the regularity index (NNRI) of the natural mosaic. Scale bars: 100 µm. (1) The natural mosaics adapted from Reference 4. (2) The artificial mosaics generated by the O-PIPP approach. (3) The distributions of NN distances in natural mosaics (gray), overlaid by values extracted from O-PIPP–simulated mosaics (transparent red). (4) Boxplots of NNRIs of the single mosaic simulated by the O-PIPP approach, the PIPP model, and the d_min model. (5) The distributions of VD areas in natural mosaics (gray), overlaid by values extracted from O-PIPP-generated mosaics (transparent red). (6) Boxplots of the VDRIs of the single mosaics simulated by the O-PIPP approach, the PIPP model, and the d_min model. (7) The loss of simulated mosaics.

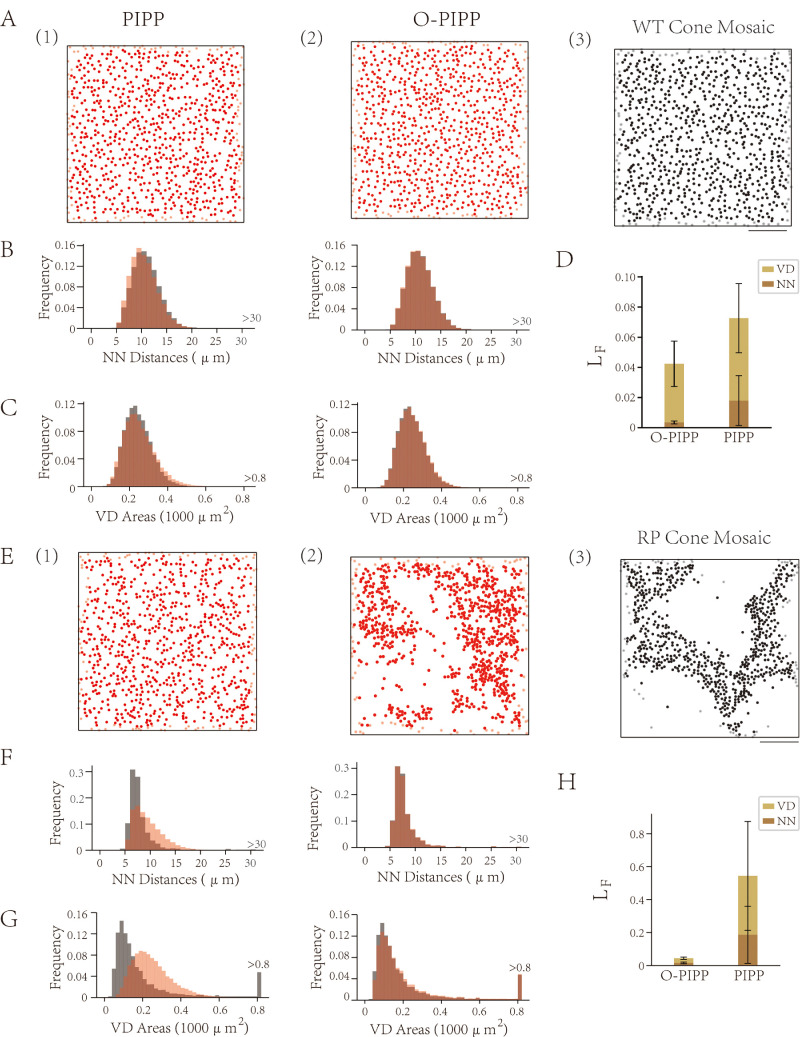
Figure 3.

Simulation results with the O-PIPP approach and the PIPP model on RP retinal mosaics. (A) Sample mosaics from PIPP-simulated WT mosaics (1), O-PIPP–simulated WT mosaics (2), and natural WT mosaics (3; adapted from Ref. 9). (B) The distributions of NN distances in natural WT mosaics (gray), overlaid by values extracted from PIPP-simulated WT mosaics (left, transparent red) and O-PIPP–simulated WT mosaics (right, transparent red). (C) The distributions of VD areas in natural WT mosaics (gray), overlaid by values extracted from PIPP-simulated WT mosaics (left, transparent red) and O-PIPP–simulated WT mosaics (right, transparent red). (D) The loss of simulated WT cone mosaics. (E) Sample mosaics from PIPP-simulated RP mosaics (1), O-PIPP–simulated RP mosaics (2), and the natural RP mosaic (3; adapted from Ref. 9). (F) The distributions of NN distances in natural RP mosaics (gray), overlaid by values extracted from PIPP-simulated RP mosaics (left, transparent red) and O-PIPP–simulated RP mosaics (right, transparent red). (G) The distributions of VD areas in natural RP mosaics (gray), overlaid by values extracted from PIPP-simulated RP mosaics (left, transparent red) and O-PIPP–simulated RP mosaics (right, transparent red). (H) The loss of simulated RP cone mosaics.

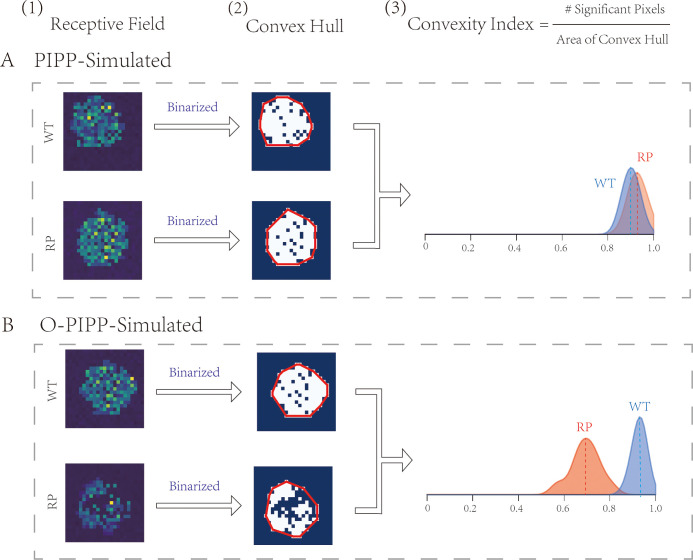
Figure 4.

Receptive fields of GCs in retinal neural networks. (A) The RFs (1) and the binarized RFs (2) of the GCs from an O-PIPP–simulated RP retinal network and an O-PIPP–simulated WT retinal network. Distributions of CIs of GC RFs from two populations of networks (3). (B) The RFs (1) and the binarized RFs (2) of the GCs from a PIPP-simulated RP retinal network and a PIPP-simulated WT retinal network. (3) Distributions of CIs of GC RFs from two populations of networks.

O-PIPP Shows More Precise Modeling of WT Retinal Mosaics

To validate the versatility and superiority of the O-PIPP, we modeled seven retinal mosaic patterns (Fig. 2; Supplementary Tables S2–S4). These mosaics came from WT healthy animals, and their patterns ranged from semi-near regular to near-random distribution.⁴ It is not difficult to observe that random examples from the simulated mosaics by the O-PIPP (Fig. 2[2]) exhibit significant similarity with data samples (Fig. 2[1]). In each mosaic pattern, the statistics of both the NN distance (Fig. 2[3], red) and VD area (Fig. 2[5], red) could fit very well with those from data samples (Figs. 2[3] and 2[5], gray). However, mosaics generated by PIPP and d_min displayed different degrees of similarity with sample data across diverse mosaic patterns (Supplementary Fig. S7)—for example, the type 4 BC mosaic simulated by the PIPP (Supplementary Figs. S7A[2] and S7A[3]) and the VGluT3 amacrine cell mosaic simulated by d_min (Supplementary Figs. S7E[5] and S7E[6]). Additionally, we randomly selected three examples from the simulation results of horizontal cells to demonstrate the influence of stochastic factors on model outcomes (Supplementary Fig. S8). From two key spatial metrics, NNRI (Fig. 2[4]) and VDRI (Fig. 2[6]), it is clear that the mosaic models through the O-PIPP reproduced data samples (the red dashed lines) much more stably and precisely than the other two. The NN (Fig. 2[7], brown) and VD (Fig. 2[7], yellow) KL divergence, which evaluated the distribution similarity between models and data, also quantitatively describe the better reproduction of the O-PIPP (the lower, the better). In summary, the O-PIPP simulated mosaics could reproduce the spatial features of data samples more accurately and robustly than the other two methods.

O-PIPP Can Model Abnormal RP Mosaics

The O-PIPP is also superior in its ability to model abnormal mosaic patterns, which cannot be well solved by the classic PIPP. To prove this, we modeled the cone mosaic from WT and RP rats⁹ with the PIPP and O-PIPP. In the situation of modeling the WT cone mosaic that had a normal mosaic pattern, the result was the same as the cases in Figure 2. Both the PIPP and the O-PIPP could simulate similar mosaics as the data sample (Fig. 3A), even though the O-PIPP displayed greater similarity with regard to NN distance (Fig. 3B), VD area (Fig. 3C), and KL divergence (Fig. 3D). Much more obvious performance differences were observed when modeling the RP cone mosaic. The PIPP failed to accurately model the RP cone mosaic pattern, as shown in Figure 3E. However, with the O-PIPP (Fig. 3E[2]), we reproduced the data sample mosaic pattern easily by defining an optimization function with target spatial features. Results for NN distance (Fig. 3F), VD area (Fig. 3G), and KL divergence (Fig. 3H) reveal the distinct performance between the PIPP and the O-PIPP (note the tail of VD area in Fig. 3G and unseen O-PIPP KL divergence in Fig. 3H). In short, the O-PIPP could model disease retinal mosaics by defining a suitable optimization function, remedying the PIPP limitation.

Retinal Circuitry Model With RP Cone Mosaics Reproduces Alteration on GC RFs

Modeling abnormal mosaics has significant meaning in the study of retinal disease. It is well known that photoreceptor loss and mosaic rearrangement are typical characteristics of the RP retina, but their effects on retinal circuitry and function remain to be investigated. Computational modeling can facilitate the exploration based on experimental research. Therefore, after obtaining cone mosaics, we developed a three-layer discrete neuronal network model (Supplementary Fig. S6). With these models, we could obtain the corresponding GC RF through spike-triggered average analysis (Fig. 4[1], Supplementary Fig. S9).³² Binarization of the RF yielded the convex hull (Fig. 4[2]), and the convexity index (CI) was the quantitative description of the convex hull (Fig. 4[3]).³⁸ Because the PIPP could not model the RP cone mosaic well, we could not distinguish between the RFs and convex hulls nor the distribution of CIs between PIPP-simulated WT and RP retinas (Fig. 4A). However, with the O-PIPP, both the WT and RP cone mosaic models were much more biologically plausible, as well as the GC RFs (Fig. 4B[1]) and corresponding convex hulls (Fig. 4B[2]). Of greatest importance is that the RF CIs had wider distributions and smaller peak values, which was also observed in experimental recordings.³⁸ In conclusion, better retinal mosaic models could contribute to more biologically plausible retinal circuitry models, which have the potential to promote our understanding of retinal diseases.

Discussion

Overall, we provide a more precise and universal mosaic generation method, the O-PIPP approach. We demonstrated its advantages by simulating various neural spatial organizations, including different healthy mosaics⁴ and clustered RP mosaics.⁹ Additionally, we exhibited the ability of biologically plausible retinal discrete neuronal network models to reproduce experimental observations.³⁸ Our findings suggest the significance and potential of the O-PIPP in retinal computational modeling research, which will be helpful to many studies, such as retinal development, retinal diseases, retinal circuits, and neural computations in visual information processing.

Advantages of the O-PIPP Compared With the PIPP

The core of the PIPP, the interaction function, only describes the local spatial features of cells and is insufficient for describing spatial features on a larger scale. Therefore, the PIPP does not perform well in modeling mosaics in certain disease states, which limits its broader application. To address this, we introduced an optimization process based on PIPP. By designing optimization objectives, we can constrain the spatial features of mosaics on a larger spatial scale. Experiments have shown that this optimization process not only enables the modeling of special disease mosaic patterns but also significantly improves the accuracy of conventional mosaic modeling (Figs. 2, 3).

Moreover, the optimization objectives are not limited to spatial features. By using the connection relationships of cells under disease conditions as constraints, we successfully modeled the spatial distribution of bipolar cells in RP states (Supplementary Fig. S6). The resulting retinal network model accurately reproduces the physiological characteristics observed in actual experiments (Fig. 4).

In theory, the O-PIPP can be implemented independently of the PIPP, as the interaction function can be replaced by other local updation rules. The widespread use of the PIPP makes developing the O-PIPP based on the PIPP an optimal choice. This allows the O-PIPP to fully leverage the existing advantages of the PIPP while ensuring sufficient compatibility, which facilitates quicker adoption of the O-PIPP by researchers in the field.

Reason for the Current Methodology

Selecting Simulated Annealing in Optimization

The optimization stage in the O-PIPP serves as an engine that drives the mosaic toward specific spatial or connecting features. In this work, we employed the simulated annealing algorithm due to two requirements arising from the mosaic application: (1) the algorithm must function without differentiable loss functions, given the complexity of feature calculations, and (2) it must introduce randomness into the process to generate massive mosaics from a single starting value. These requirements exclude many optimization algorithms in computer science, such as gradient-based searches³⁹ and grid search algorithms. In theory, several other optimization algorithms may also be suitable, particularly methods within metaheuristic techniques.⁴⁰ This remains open for further research.

Selecting NN and VD as Evaluation Metrics

Metrics that describe spatial patterns of retinal mosaics are mainly adopted from computational geometry and point pattern analysis.⁴¹ Various metrics have been applied in retinal mosaics analysis, including the NN distance or the VD area in this work, and several distance-based functions to describe the correlation among points (L, G functions).^4,30 Also, previous work has proposed spatial autocorrelation-related metrics for retinal mosaics, such as the effective radius and the packing factor.⁴²

We selected the NN distance, VD area, and their probability distributions in our study for the following reasons: (1) Their numerical values can be obtained from one real mosaic figure. (2) They are reliable in distinguishing minor differences between two mosaics by relocating a small partition of cells. (3) They provide sufficient constraints for capturing the retinal mosaics spatial pattern compared to metrics; for example, the G function is the cumulative frequency distribution of NN distances, and the L function is the cumulative frequency distribution of cell–cell distances.⁴ The effective radius and the packing factor⁴² are further calculations based on the L function and therefore do not provide more information. (4) They are widely used in retinal mosaic research, and their corresponding physical spatial meanings are easy to understand.^43–45

Significance and Potential Applications of More Realistic Mosaics Modeling

More than 60 types of retinal cells form different mosaic distribution patterns to sample specific types of visual information. The mechanisms behind the formation of these specific mosaic patterns have always been a fundamental research topic. At the same time, understanding the relationship between these mosaic patterns and visual functions is also a significant theme.

One key research area involves exploring the correlation between photoreceptor mosaic changes and visual function in disease states by combining in vivo retinal imaging and visual function tests.^46–50 Similar studies on animals^9,51,52 can more easily recruit ex vivo techniques. In this paper, we have demonstrated how O-PIPP provides a supplementary approach to exploring the underlying mechanisms between abnormal retinal structure and visual function loss.

Another research area aims to uncover how healthy retinal mosaics directly influence visual processing, and this is where mathematical and computational modeling is more widely used. The most straightforward perspective is to regard photoreceptor mosaics as sampling devices, using computational simulations to assess how different mosaics impact signal sampling.⁵³ Typically, these simulations consider only regular and irregular mosaic patterns. Similarly, retinal ganglion cells (RGCs) are often regarded as feature extractors in visual pathways. Efficient coding models have shown that coordinating retinal receptive fields among rats and primates, particularly the intermosaic coordination of ON and OFF RGCs, optimized information transmission.^12,54 However, current retinal network models typically organize homotypic cells into grid arrays, ignoring type-specific spatial organizations and neural connections based on relative arbor distances (reviewed in Ref. 55). Other theoretical models simulate disease-induced changes in the retina using a well-mixed schema, where a single cell represents a population, thus neglecting mosaic-specific spatial effects (reviewed in Ref. 56). In the downstream visual pathway of retinas, RGC mosaics modeled as hexagonal lattices were initially thought to shape orientation maps in the visual cortex.⁵⁷ More realistic RGC mosaic models using PIPP have evolved different perspectives.⁵⁸ Similarly, applying O-PIPP in the aforementioned models can enhance their biological realism, helping us to understand the relationship between structure and function through computational modeling.

To sum up, by bridging the gap between anatomical observations and computational models, the O-PIPP can help to provide a more comprehensive understanding of the intricacies of retinal development, retinal diseases, and neural computations in visual information processing.