Functional architecture of intracellular oscillations in hippocampal dendrites

Abstract

Fast electrical signaling in dendrites is central to neural computations that support adaptive behaviors. Conventional techniques lack temporal and spatial resolution and the ability to track underlying membrane potential dynamics present across the complex three-dimensional dendritic arbor in vivo. Here, we perform fast two-photon imaging of dendritic and somatic membrane potential dynamics in single pyramidal cells in the CA1 region of the mouse hippocampus during awake behavior. We study the dynamics of subthreshold membrane potential and suprathreshold dendritic events throughout the dendritic arbor in vivo by combining voltage imaging with simultaneous local field potential recording, post hoc morphological reconstruction, and a spatial navigation task. We systematically quantify the modulation of local event rates by locomotion in distinct dendritic regions, report an advancing gradient of dendritic theta phase along the basal-tuft axis, and describe a predominant hyperpolarization of the dendritic arbor during sharp-wave ripples. Finally, we find that spatial tuning of dendritic representations dynamically reorganizes following place field formation. Our data reveal how the organization of electrical signaling in dendrites maps onto the anatomy of the dendritic tree across behavior, oscillatory network, and functional cell states.

Neurons receive their input in three dimensions via their dendrites, but how electrical activity in dendrites is organized is unknown. Here, the authors work out the distinct rules that govern activity across this 3D structure in different brain states.

Introduction

Electrical activity in the nervous system is organized on multiple spatial and temporal scales^1–6 and controls animal behavior. During locomotion, single unit activity and local-field potential (LFP) in the hippocampal formation both show modulation in the theta frequency band (5–10 Hz), whereas during awake immobility, brief high-frequency sharp-wave ripple (SWR) oscillations (80–220 Hz) associated with memory consolidation are present^6–8. Although the participation and connectivity of different cell types in these network states have been well documented, how converging excitation and inhibition interact within active dendrites⁹ to modulate the local membrane potential across these states is not known.

To study this question, we focused our attention on hippocampal CA1-area pyramidal cells (CA1PCs), which receive topographically organized synaptic inputs from distinct neuronal populations¹⁰. In addition to this anatomical organization, incoming population-level synaptic activity is temporally structured, as can be seen in measurements of alternating current sinks and sources in LFP across the hippocampal strata. With competing passive and active propagation of signals within dendrites, we hypothesized that such spatially and temporally structured inputs will give rise to similarly structured membrane potential dynamics, which in turn will affect how inputs are integrated. Changes in behavioral state also drastically affect the participation of different classes of interneurons¹¹ that preferentially inhibit excitatory inputs at distinct locations across the dendritic tree, giving rise to complex membrane potential dynamics that demand empirical study.

Cortical dendrites are seldom accessible to direct electrophysiological recordings in vivo^12–14, and have primarily been studied either in vitro^15,16 or indirectly by optical imaging of calcium sensors in vivo^13,17–25. Due to technical limitations, it has not been previously possible to interrogate dendritic membrane potential dynamics repeatedly at multiple locations across the dendritic tree of the same cell in the awake, behaving animal.

Genetically encoded voltage indicators (GEVIs) have recently emerged as promising tools for fast optical recording of neural circuit dynamics^26–29. To study the relationship between subcellular voltage dynamics, integration of synaptic inputs and changes in network states in vivo relevant for spatial navigation and episodic memory^5,18,30–35, we electroporated ASAP3²⁷ into single CA1PCs and performed two-photon voltage imaging across their dendritic trees. Using concurrent hippocampal LFP recordings, we investigated the relationship between local dendritic voltage dynamics and two physiologically antagonistic population patterns: the locomotion-associated theta rhythm and the immobility-associated SWR. Finally, using a random-foraging behavioral task on cued belts, we characterized dendritic electrical signaling as a function of a cell’s place tuning. Our results reveal dynamic compartmentalization of intracellular voltage signals that depends on behavioral, network, and cellular states within the dendritic arbor of CA1PCs in vivo.

Results

Two-photon voltage imaging dendritic activity in vivo

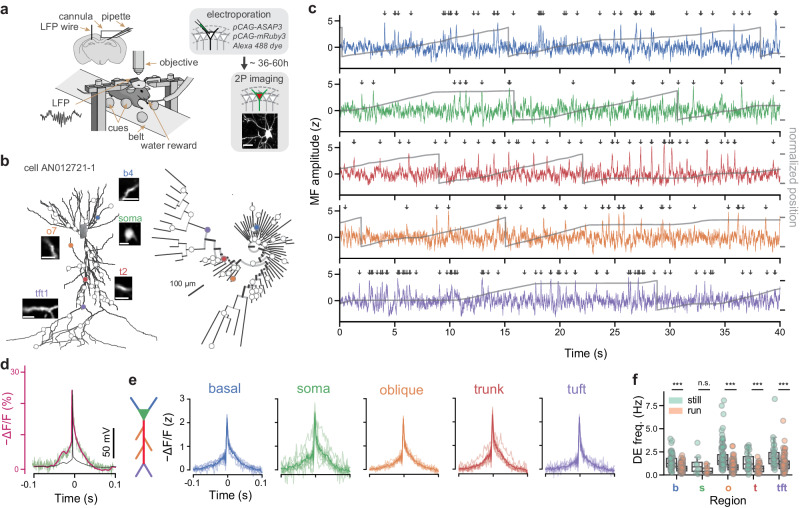
To investigate electrical signaling in dendrites of CA1PCs in behaving mice, we performed in vivo single-cell electroporation (SCE) under two-photon microscopy guidance^36–38 to deliver plasmids for stable expression of ASAP3 (Fig S1), a green-fluorescent GEVI developed and characterized for use in vivo²⁷, along with mRuby3³⁹, a static red-fluorescent morphological filler protein (see Methods). Simultaneous two-photon ASAP3-voltage imaging of CA1PCs and contralateral LFP recordings⁴⁰ were performed in head-fixed mice during volitional running and immobility on a cued treadmill⁴¹ (Figs. 1a, S2a, b, see Methods). Our SCE procedure allowed for bright labeling of fine dendrites and post hoc full reconstruction of cell morphology (Fig. 1b). In this work, we introduce phylogenetic dendrograms ("phylograms”) to render 3D dendritic morphology in two dimensions (Fig. 1b, right; also see Methods). ASAP3 fluorescence was sampled at a frame rate of 440 Hz over a period of 30–45 s from 28–64 (median: 43, IQR: 10.75) regions of interest (ROIs) along the dendritic arbor (Figs. 1c, S2c). Our labeling and recording configuration allowed for the detection of depolarizing events (DEs, Fig. 1c) using a matched-filter approach (Figs. S2d, e, S3–S5).

Fig. 1. Detection and organization of depolarizing events (DEs) across the dendritic arbor and behavioral states.

a Experimental setup. Electroporation-imaging cannula window was implanted above the right dorsal hippocampal area CA1. A tungsten wire LFP electrode was inserted contralaterally, within or in proximity to the CA1 cell body layer. Mice were habituated using water rewards to run on a cued belt treadmill. ASAP3 and mRuby3 plasmids were single-cell electroporated (SCE) in CA1 pyramidal cells under two-photon microscopy guidance. Two-photon fluorescence measurements were obtained after approx. 36 hours post SCE from several tens of dendritic regions of interest (ROIs) across the whole dendritic tree. Scale bar 25 μm. b Morphological reconstruction and identification of recording locations. Left: two-photon microscopy stacks were acquired in vivo following each imaging session and neuronal morphologies were reconstructed (example cell AN012721-1). Inset scans show the extent of dendritic (basal: b4, trunk: t2, oblique: o7, tuft: tft1) and somatic imaging regions (scale bars 10μm). Right: phylogram representation of the same cell’s branching morphology, with radial distance from soma representing path distance to each recording location. Circles indicate imaging locations. c Example optical measurements of sequentially recorded dendritic electrical activity from cell shown in (b) during bouts of locomotion and rest. Optical signals were sampled at 440 Hz, stabilized against movement artifacts during locomotion epochs, match-filtered (MF) and thresholded for depolarizing event (DE) detection (arrows) (see Methods). Note that ASAP3 fluorescence is plotted as  − ΔF/F to reflect the direction of change in the membrane potential. Gray traces: animal position during the recording. d Electrophysiological calibration: A somatically recorded CA1PC action potential (black) was played through voltage-clamped ASAP3-expressing HEK293 cells at 37 °C and the corresponding ASAP3 fluorescence response (green) was recorded. Magenta: Markov model predicted ASAP3 response. For a detailed analysis of the Markov model, see Fig. S3. e Average z-scored DE waveforms for isolated events pooled from different dendritic domains with a fluorescence baseline SNR>10 (calibrated against a shot-noise baseline) during locomotion and immobility behavior states (N = 13 cells from 9 mice, colored curves). f DE frequency is reduced during locomotion states compared to immobility across all dendritic domains for fluorescence baseline SNR>10 (basal: p = 10⁻¹⁰, oblique: p = 2 × 10⁻¹⁵, soma: p = 0.03, trunk: p = 2 × 10⁻⁶, tuft: p = 4 × 10⁻⁵, Wilcoxon paired test; 587 dendrites from 13 cells). Two-way ANOVA for frequency: p = 3 × 10⁻¹¹, main effect of region; p = 1 × 10⁻⁴¹, main effect of locomotion; F(4, 770) = 2.24, p = 0.06 region × locomotion interaction. Box: Q1, Q2, Q3; whiskers: range (excluding outliers). Points represent individual dendrites. α = 0.01 indicates significance for post hoc tests at the per-region level using Bonferroni’s correction.

To better understand the voltage-to-fluorescence transformation of ASAP3, we modeled sensor dynamics using a 4-state Markov chain based on recordings from ASAP3-expressing voltage-clamped HEK293 cells (Figs. 1d, S3, see Methods). We then compared the model-predicted ASAP3 response to single action potentials recorded in vivo to detect DEs in our dataset, and found close qualitative agreement (Fig. 1d, see Methods). The average DE waveform detected using our method was qualitatively similar across dendritic domains Fig. 1e and between running and immobile behavior states (Figs. S2b, S6). Across behavior states, the soma fired at an average of 0.67 ± 0.14 Hz. Mean DE frequency differed significantly between dendritic regions (basal: 0.89 ± 0.03 Hz, trunk: 0.93 ± 0.08, oblique: 1.1 ± 0.04, tuft: 1.4 ± 0.08; Kruskal–Wallis H test, H = 37.8, p = 3 × 10⁻⁸) but did not vary as a function of distance along the basal-apical axis (Fig. S6a). DE frequency decreased across all cellular domains during locomotion compared to rest (Fig. 1f). These results demonstrate that DEs with fast sodium spike-like kinetics are detectable with voltage imaging across behavioral states and dendritic regions of CA1PCs in vivo. Throughout the remainder of this work, DEs refer to fast sodium spike-like events, likely representing locally generated or backpropagating individual spikes in dendrites, detected using a matched filter based on a template calibrated to simultaneous patch-clamp and voltage imaging in an in vitro preparation (Methods). We also observed a smaller proportion of longer duration dendritic events in all dendritic regions (10.4% of all events, 56.2 ± 2.2 ms, mean  ± s.e.m.), likely representing a combination of sodium spikes and a slower, NMDA receptor/voltage-gated calcium channel-mediated component (plateau-bursts)^42,43 using a template constructed from dendritic patch-clamp recordings from CA1 acute slices (Fig. S7a)⁴⁴. Our fast voltage imaging approach necessitates sequential scanning of ROIs, which does not allow for disambiguation of backpropagating action potentials from locally generated dendritic spikes or an exhaustive characterization of the diversity of dendritic events. In the remainder of this work, we characterize dendritic signaling in the online (locomotor) and offline (immobile) states using subthreshold membrane voltage and suprathreshold fast DEs.

Theta oscillation-related modulation of dendritic membrane potential

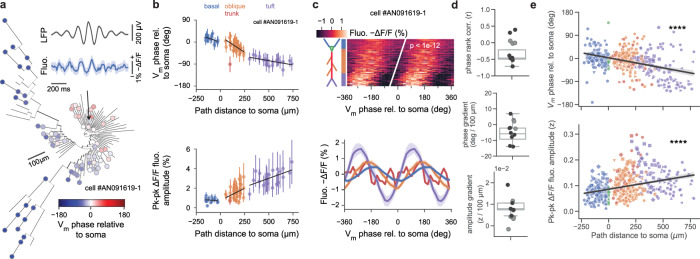
When an animal is moving, a 5–10 Hz extracellular oscillation (“theta”) emerges in the hippocampus, which is thought to reflect the “online” state of the brain and support memory encoding and decoding⁸. Layer-dependent organization of theta has been proposed based on extracellular recordings and recordings in anesthetized animals⁸. Here, we investigated the relationship between extracellular theta and intracellular membrane potential across the entire dendritic tree in the awake, behaving animal. Previous work has found high coherence between interhemispheric hippocampal theta oscillations^45,46; in order to avoid electrical artifacts induced by imaging, we imaged membrane potential while simultaneously recording LFP in contralateral CA1 (see Methods). Out of N = 11 cells, ASAP3 fluorescence from 83% basal, 100% somatic, 97% trunk, 91% oblique and 93% tuft ROIs was found to be theta-band modulated (example cell in Fig. 2a, see Methods). Morphological reconstruction revealed that theta oscillation amplitude and phase changed gradually across the dendritic tree as a function of somatic path distance to the recorded ROI (example cell in Fig. 2b, top, middle, Fig. 2c, additional examples in Fig. S8). Regression analysis of imaged ROIs within the same cell showed a significant gradient of theta-band fluorescence oscillation phase relative to the somatic compartment along the basal-tuft axis for 8/11 cells, with 7/8 showing an advancing gradient toward the tuft (Fig. 2d, top, middle). The average theta-band fluorescence oscillation amplitude of theta-modulated ROIs was also found to increase from basal toward the tuft domain (Fig. 2d, bottom). Pooling ROIs across cells, starting from the distalmost basal and progressing toward distalmost tuft dendritic ROIs, the fluorescence oscillation phase advanced along the basal-tuft axis with a slope of  −7.9°/100 μm while oscillation amplitude increased with a slope of  0.7%z/100 μm (Fig. 2e).

Fig. 2. Theta oscillation is organized across the dendritic tree as a traveling wave.

a Phylogram of fluorescence phase at recording locations, relative to estimated somatic phase (all regions showed significant sinusoidal phase modulation at p < 0.05 under a modified one-sided Z-test without multiple comparisons correction). Inset, top: Contralaterally-recorded extracellular theta-band-filtered (5–10 Hz) local-field potential (mean with 95% CI); Bottom: Cycle-averaged fluorescence oscillation of a basal dendritic segment (arrow, mean with 95% CI). b Dendritic tree gradients in theta oscillation phase, amplitude and DE phase for example cell in (a) during locomotion epochs. Top: Membrane potential oscillation phase advances along the basal-tuft axis relative to somatic phase (zero phase corresponds to a trough in somatic membrane potential oscillation). Region linear regression fits: phase dependence: basal (n = 20 segments, r² = 0.27, p = 0.04), oblique (n = 46 segments, r² = 0.39, p < 0.01), tuft (n = 20 segments, r² = 0.32, p = 0.01); overall (r = − 0.89, p < 6 × 10⁻²⁷). Bottom: Membrane potential oscillation amplitude increases along the basal-tuft axis. Region fits (same n as above): basal (r² = 0.02, p = 0.62), oblique (r² = 0.13, p = 0.02), tuft (r² = 0.30, p = 0.01); overall (r = 0.84, p < 2 × 10⁻²¹). Data are presented as mean values ± SEM. c Subthreshold theta-band membrane potential oscillation is a traveling wave across the basal-tuft dendritic tree axis. Top: Heatmap of mean phase-binned fluorescence vs soma path-distance rank along basal-tuft axis for example cell in a (two cycles shown) with rank-regression line (Pearson’s r = − 0.70, p < 10⁻¹²). Vertical axis colored by cell region. Bottom: Cycle-averaged mean fluorescence (±bootstrapped 95% c.i.) of example cell as a function of theta phase relative to somatic phase. d Top: Correlation coefficients from rank-regression shown in c (top) of path-distance to soma vs phase bin of minimum. 8/11 cells recorded exhibit a significant phase gradient along the basal-tuft axis (black dots: significant cells; gray dots: nonsignificant cells), with 6/8 having a negative (advancing) gradient. Middle: Phase gradients from least-squares fit as in e calculated per-cell. 8/11 cells recorded show a significant phase gradient along the basal-tuft axis, with 7/8 having a negative (advancing) gradient. Bottom: Z-score amplitude gradients from least-squares fit as in (e) calculated per cell. 5/11 cells recorded exhibit a significant increasing gradient along the basal-tuft axis. e Population summary of theta-band membrane potential oscillation phase and amplitude gradients by recording segment during locomotion epochs. (colors: regions, markers: N = 11 unique cells). Top: Theta-band membrane potential oscillation phase advances with distance from basal to tuft regions (slope  = − 7. 9°/100μm, Pearson’s r: r = − 0.41, p = 1 × 10⁻¹⁹, Spearman’s rho: ρ = − 0.35, p = 2 × 10⁻¹⁴). Bottom: Theta-band membrane potential oscillation z-score amplitude increases with distance from basal to tuft regions. (slope  = 0.7%z/100 μm, Pearson’s r: r = 0.32, p = 8⁻¹³, Spearman’s rho: ρ = 0.37, p = 1 × 10⁻¹⁶). Regression line is shown with a 95% bootstrapped confidence interval.

Theta phase preference of dendritic events

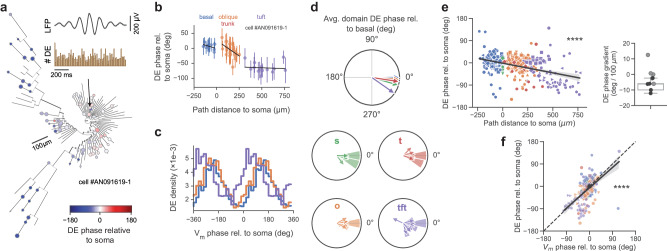
Somatic spikes occur preferentially at the extracellular theta trough, corresponding to the peak of the intracellular theta oscillation⁸. We asked if the same was true in dendrites. We found that gradients in theta phase and amplitude were accompanied by a comparable gradient in DE phase preference (example cell in Fig. 3a–c, resultant DE phase distributions in Fig. 3d), with DE phase advancing toward the tuft with a slope of  −7.8°/100 μm (Fig. 3e). A strong correlation between theta-band membrane-potential oscillation and DE phases was observed (Fig. 3f), with the oscillation phase showing a slight advancement compared to DE phase, indicating that at the segment level, DEs occur preferentially close to the peak of the subthreshold oscillation. We expect locally-generated events to be entrained to local theta phase (45° slope of the DE phase vs membrane potential phase relationship) and bAPs to occur preferentially at the peak of somatic theta (0° slope). The true observed slope is shallower than 45°, consistent with a mixture of local events and somatic-phase conveying back-propagating action potentials. Unlike fast DEs, the distribution of slow events appear to be concentrated around 0^∘ in all regions but the tuft (Fig. S7b). To assess whether DE properties are modulated by the subthreshold oscillation, we performed a linear-circular regression of DE peak amplitude against DE phase (see Methods). DE amplitude was not strongly modulated by theta phase in any regions other than the tuft (p < 4 × 10⁻⁵, Fig. S9).

Fig. 3. Depolarizing events are organized across the dendritic tree by local theta oscillations.

a Phylogram of depolarizing event (DE) phase at recording locations, relative to estimated somatic phase (all regions showed significant phase modulation at p < 0.05 under a modified one-sided Z-test without multiple comparisons correction). Inset, top: Same contralaterally-recorded extracellular theta-band-filtered (5–10 Hz) local-field potential as in Fig. 2 (mean with 95% CI); Bottom: DE histogram, with DEs occurring preferentially at the peak of intracellular theta oscillation. b Dendritic tree gradient in DE phase for example cell in (a) during locomotion epochs. DE preferred phase advances along the basal-tuft axis relative to somatic DE phase. Region linear regression fits: basal (n = 20 segments, r² = 0.18, p = 0.2), oblique (n = 46 segments, r² = 0.2, p = 0.02), tuft (n = 20 segments, r² = 0.01, p = 0.79); overall (r = − 0.81, p = 4 × 10⁻¹³). Data are presented as mean values +/- SEM. c Histogram of DE densities for the same example cell vs theta phase in the basal, oblique, trunk, and tuft domains relative to somatic membrane potential oscillation phase (two cycles shown, zero phase corresponds to estimated trough of somatic theta). DE density was defined as the DE rate (events / second) in each phase bin. d Resultant phase of DEs (relative to basal mean phase) also changed gradually along the basal-tuft axis. ROI preferred phases (histograms) and cell means (arrows) by region. e Left: Theta-band DE phase preference gradient across the basal-tuft axis relative to soma (slope  = − 7. 8°/100 μm, r = − 0.41, p = 10⁻¹⁴). Regression line shown with 95% bootstrapped confidence interval. Right: Strength of DE phase gradient by cell (significant cells in black, 5/10; boxplot significant only). f Dendritic DEs preferentially occur close to the peak of local theta-band dendritic membrane potential oscillations. Linear regression of DE resultant phase vs theta-band membrane potential oscillation phase, by recording segment (slope  = 0.91 ± 0.07 (mean  ± s.e.m.), (0.77, 1.04) 95% CI, r = 0.59, p = 10⁻³⁰; colors: regions; markers: cells). Unless otherwise specified, all box-and-whisker plots show Q1, Q2, Q3, and range excluding outliers; points represent individual cells; r values are Pearson’s r; using Bonferroni correction α = 0.01 for post hoc tests performed on the per-region level, α = 0.05 for all other tests.

We then asked whether these gradients were explained by absolute distance from the soma or distance along the basal-apical axis. We focused on trunk and oblique segments, decomposing the total somatic path distance into an along-trunk component and an away from the trunk (oblique) component. Multivariate regression against these two components revealed that the observed gradients did not advance significantly along radial obliques dendrites; rather, they could be explained solely by the distance along the soma-trunk axis (Fig. S10). With these results, we comprehensively characterize subcellular theta oscillations across the CA1PC dendritic tree in the behaving animal, revealing strong correlation between the phase of local dendritic events and dendritic membrane theta phase.

SWR-related modulation of dendritic membrane potential

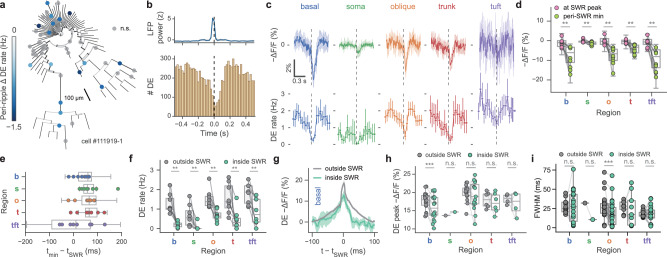
Hippocampal dynamics during immobility (the “offline” state) differ considerably from online dynamics during locomotion. The theta oscillation disappears when an animal is immobile, while the sharp-wave ripple (SWR) emerges. SWRs are critical for offline memory consolidation, but like theta, have thus far primarily been studied at the somatic compartment. Here, we examine dendritic signaling across the arbor inside and outside of SWRs⁷. Overall, dendrites fired at 0.50 ± 0.08 Hz inside of SWRs compared to 1.50 ± 0.17 Hz (mean  ± s.e.m.) during immobility outside of SWRs. On average, 17.6 ± 3% of each cell’s dendrites (mean  ± s.e.m., N = 8 cells) were significantly modulated by SWRs; 98.3% of modulated dendrites showed a reduction in DE rate inside SWRs compared to immobility baseline outside of SWRs (example cell in Fig. 4a, more cells in Fig. S11). In a  ± 500 ms peri-SWR window, we found a net suppression of dendritic DEs, which begins approximately 200 ms prior to SWR onset, reaching a nadir shortly after the peak of SWR power, and returning to baseline 200 ms after SWR peak (Fig. 4b). We dissected this effect by dendritic region, and found that SWRs on average are associated with an acute hyperpolarization of dendritic membrane potential in every region, which reaches a nadir shortly after the SWR LFP power peak (Fig. 4c, top). However, individual SWR responses are highly heterogeneous; while the predominant effect is inhibition, a minority of SWRs recruit the recorded dendrite (Fig. S12). In each region, fluorescence showed maximal membrane potential hyperpolarization that was delayed from the SWR LFP peak power (baseline = 0% − ΔF/F, Fig. 4d, e, Tables S4, S5). The timing of this effect was fairly consistent between cells and along the basal-tuft axis (Fig. S13). Concomitantly, we found an acute reduction in DE rate in the soma and all regions of the arbor (Fig. 4c, bottom, Fig. 4f, Table S6). Similar to fast DEs, slow events were also suppressed around SWRs (Fig. S7c). Given that different subtypes of GABAergic interneurons are differentially recruited to SWRs and target distinct dendritic domains¹¹, we asked whether DEs occurring during SWRs differed from those occurring outside SWRs in each region. Unlike somatic action potentials, local dendritic events are not stereotyped or all-or-none, but vary in their amplitude and morphology^42,47–52 which may be modulated by oscillations^50,53. We found that DE amplitudes were significantly decreased (Fig. 4g) inside SWR epochs for the basal domain (outside: 18.9%  − ΔF/F, 95% CI [18.1,19.5], inside: 15.7%  − ΔF/F, 95% CI [13.9,18.3]; Fig. 4h, Table S7), while amplitude was preserved but DE width was significantly narrowed in the oblique domain (outside: 26.0 ms, 95% CI [20.0, 30.1]; inside: 16.1 ms 95% CI [12.6, 21.7]; Fig. 4i, Table S8); other regions did not exhibit significant differences in these parameters. In summary, we found that SWRs on average are associated with an inhibitory effect on the dendritic arbor, in membrane potential, DE rate, and DE waveform shape in the basal and oblique domains. This cell-wide inhibition begins preceding the peak of SWR power, peaks shortly after SWR LFP power peak, and recedes about 200 ms after the peak.

Fig. 4. Sharp-wave ripple-associated modulation of dendritic electrical signaling.

a Example phylogram of a reconstructed cell (cell #111919-1) with significantly SWR-modulated recording locations colored by DE rate change inside minus outside of ripple epoch (gray: p > 0.05, two-tailed Poisson rate test). Significantly modulated recording locations show a suppression of DE rate during SWRs. b Top: Mean z-scored LFP power in ripple band. Bottom: Peri-SWR spike time histogram (all regions, N = 8 cells). c SWR-associated changes in fluorescence show hyperpolarization of membrane potential (top) and reduction in DE rate across the soma and dendritic arbor (bottom); average of N = 8 cells with 95% CI. Note trough of membrane potential hyperpolarization is visibly delayed with respect to SWR LFP peak power (dashed vertical lines) in most cellular compartments. Due to high background levels of internal membrane-bound ASAP3 in the somatic compartment, absolute fluorescence changes recorded from the soma are smaller compared to dendrites. d SWR-associated hyperpolarization from c (top). Mean amplitudes ( − ΔF/F) at peak of ripple power (pink), vs minimum in expanded SWR window (ripple peak  ± 100 ms; light green). Two-way ANOVA for membrane potential: p = 5 × 10⁻⁵, main effect of region; p = 2 × 10⁻¹³, main effect of SWR modulation; F(4, 69) = 5.55, p = 6 × 10⁻⁴ interaction of SWR × region. Maximal voltage hyperpolarization lags ripple power (p = 0.008 for all regions, Wilcoxon paired test). e Mean time of maximal membrane potential hyperpolarization of d with regard to SWR LFP peak power. f SWR-associated DE rate suppression from c (bottom). (p = 0.008 in all, Wilcoxon paired test). Two-way ANOVA for DE rate: p = 9 × 10⁻⁶, main effect of region; p = 7 × 10⁻¹², main effect of SWR modulation; F(4, 69) = 0.72, p = 0.58 interaction of SWR × region. g Average DE waveforms are significantly decreased in the basal domain inside SWRs (green) compared to outside SWRs (gray). Waveforms with 95% CI were filtered with a 5-point moving average. h DE peak amplitudes are slightly decreased in the basal domain inside SWRs (p = 0.006) but not significantly modulated in soma or apical domains (oblique: p = 0.42, soma: p = 1.0, trunk: p = 0.44, tuft: p = 0.63, all Wilcoxon paired test). Two-way ANOVA for DE amplitude: p = 1 × 10⁻²³, main effect of region; p = 0.0007, main effect of SWR modulation; F(4, 69) = 3.34, p = 0.01 interaction of SWR × region. i Full-width at half-max (FWHM) of regional average DE waveforms (as in g) shows significantly narrower peaks in the oblique domain (p = 0.0004, Wilcoxon paired test). Other regions were not significantly modulated (p = 1.0 for basal, soma, tuft, p = 0.57 for trunk). Two-way ANOVA for DE FWHM: p = 0.02, main effect of region; p = 0.058, main effect of SWR modulation; F(4, 158) = 1.25, p = 0.29 interaction of SWR × region. Unless otherwise specified, all box-and-whisker plots show segment-level Q1, Q2, Q3, and range excluding outliers; points represent individual cells (n = 8 cells throughout unless otherwise noted); using Bonferroni correction α = 0.01 for two-sided post hoc tests performed on the per-region level, α = 0.05 for all other tests.

Spatial tuning in dendrites of non-place cells

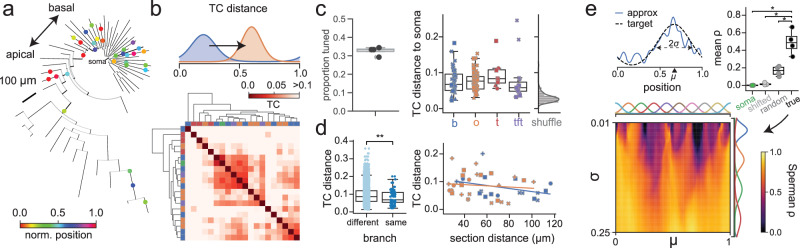
In the preceding sections, we studied the basic principles of online and offline dendritic signaling in featureless environments. We next augmented the environment with tactile and visual cues in order to study dendritic signaling during an active random foraging task on a feature-rich circular belt^41,54. We first focused on CA1PCs which did not exhibit somatic spatial tuning (“non-place” cells). We aimed to test the following hypotheses: (1) dendrites exhibit spatial tuning; (2) dendritic segments on the same branch are likely to be similarly tuned; (3) dendritic representations of single cells span the environment (Fig. 5a, individual cell example; see Fig. S14 for all recorded cells). In these non-place cells, we identified that approximately 33% of dendritic segments were spatially tuned, defined as a statistically significant spatial nonuniformity of DEs (calculated using the H statistic⁵⁵) compared to a shuffle distribution (Fig. 5c, left). We calculated the pairwise tuning curve distances⁵⁶ between these tuned segments, and found apparent cluster structure in this tuning (Fig. 5b). Even though these were non-place cells, we asked if some low baseline of somatic spatial selectivity could be driving this structure. Although there was wide variability in spatial firing between soma and dendrites in each dendritic region (Fig. 5c, right), we found that dendrites in each region were less coherent with the soma than chance, suggesting that the dendritic tuning we observed was not explainable by somatic backpropagation; rather, the dendritic arbor and the soma are compartmentalized to some extent. We then asked on what level this compartmentalization occurs: we found that the tuning curve distances between pairs of recorded locations on the same branch were significantly smaller than tuning curve distances between pairs on different branches, suggesting branch-level compartmentalization (Fig. 5d, left). However, we found no relationship of tuning curve distance and physical distance between pairs of segments along the same branch (Fig. 5d, right). The tuning of each dendrite that we observe may be determined by its presynaptic afferents, which are fixed. However, their weights may change during learning, which is the hypothesized mechanism by which somas acquire spatial selectivity⁵⁷. We finally asked how expressive the dendritic tuning we observed was. We used a simplified linear dendrite model to assess whether the measured dendritic tuning curves of a cell, taken together, were diverse enough to generate a range of tuning curves at the soma under appropriate weights (Fig. 5e; Fig. S14). We found that the observed dendritic tuning curves span the space of potential Gaussian place fields much better than the somatic tuning curve alone, the somatic tuning curve with spatially delayed copies, or the same number of linearly independent random tuning curves (Fig. 5e, top right), and reasonably broad tuning curves can be reconstructed with very high fidelity. These results illustrate that the dendritic arbors of non-place CA1PCs exhibit both striking internal organization and diversity of tuning, which may enable it to support arbitrary somatic place fields.

Fig. 5. Spatial tuning in non-place pyramidal cell dendrites.

a Example phylogram of reconstructed cell (AN061420-1), with recording locations colored by tuning curve centroid. b Example tuning curve distance (TCD, i.e. Wasserstein distance) matrix. Many segments exhibit high distance from soma. Top: Schematic of TCD calculation. TCD is normalized such that d = 1 corresponds to point masses on opposite sides of the belt. c Left: Proportion of tuned dendrites by cell, where tuning is defined as having a p-value below the 5th percentile of a random shuffle. Right: Cotuning of tuned dendrites with their respective soma. Black: N = 89 tuned dendrites from 4 cells; gray: TC distance 95th percentile from shuffle performed on each dendrite. Basal: p = 2 × 10⁻⁵, oblique: p = 8 × 10⁻⁹, trunk: p = 0.008, tuft: p = 0.02, Mann–Whitney U test. d Dendrites operate as compartments on the single-branch level. Left: Pairs of segments recorded on the same branch (n = 96 pairs) are significantly more co-tuned than pairs on different branches (n = 6568 pairs) (p = 0.0009, Mann-Whitney U test). e Arbitrary somatic tuning curves can be realized as sparse nonnegative combinations of tuned dendrites in non-place cells (n = 4 cells). Top left: Example tuning curve and approximation as weighted sum of dendrites. Top right: Mean realizability (Spearman’s ρ) of tuning curves in (bottom) using somatic tuning curve alone, somatic tuning curve with local shifts, and random tuning curves (true vs soma-only: p = 0.018, true vs soma/shifted: p = 0.007, true vs random: p = 0.006, paired t-test). Bottom: Realizability of theoretical Gaussian tuning curves parameterized by location and width as nonnegative least-squares fit from tuned dendrites. Unless otherwise specified, all box-and-whisker plots show Q1, Q2, Q3, and range excluding outliers. All statistical tests performed in a two-sided manner where relevant unless otherwise specified.

Spatial tuning in dendrites of induced place cells

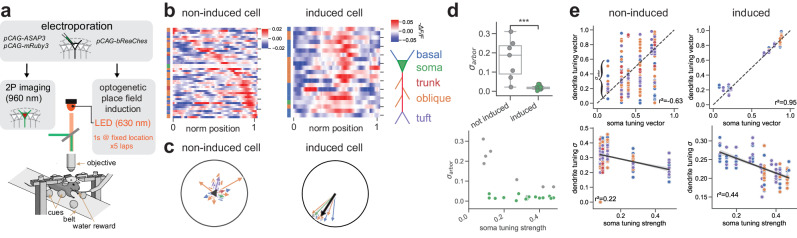
Finally, we tested the hypothesis suggested by the above model: that the diversity of dendritic tuning in non-place cells enables arbitrary place fields to be implanted at the soma. We carried out single-cell optogenetic place field induction (Fig. 6a)^25,58 and recorded activity from small, randomly selected sets of dendrites. We observed a significant increase in the coherence of dendritic tuning compared to non-induced cells and also found that this coherence corresponded well with the somatic peak (two example cells shown in Fig. 6b, c). To quantify this observation, we computed the DE tuning vector⁴¹ for each dendrite and compared the diversity among tuning vectors σ_arbor (defined as the circular standard deviation in the set of dendrite tuning directions) between induced and non-induced cells. Using this metric, we found that the arbors of induced cells showed significantly lower diversity, suggesting greater coherence in their dendritic representations (Fig. 6d, top). Rather than binarizing tuned vs untuned, we now use a continuous metric of tuning strength (defined as the normalized magnitude of the resultant vector), and observed that among the non-induced cells, stronger somatic tuning significantly inversely correlated with diversity of tuning in the arbor (r² = 0.74, p = 0.006), while induced cells exhibited low arbor tuning diversity at all soma tuning strengths (Fig. 6d, bottom). Finally, we sought to dissect these differences at the level of single dendrite-soma pairs (Fig. 6e). We found that somatic tuning is a poor predictor (r² = − 0.63) of dendritic tuning in general among non-induced cells, but a very good predictor (r² = 0.95) of tuning among induced cells. We found that the variability of a single dendrite’s tuning negatively correlates to the strength of its conjugate soma tuning in both non-induced (r² = 0.22) and induced (r² = 0.44) cells. Interestingly, we find that place cell induction also serves to similarly organize slow plateau events in induced place cells compared to noninduced place cells (Fig. S7d). Together with our previous results, these findings suggest that somatic place field acquisition reorganizes the predominant patterns of electrical activity observed at dendrites.

Fig. 6. Spatial tuning in pyramidal cells dendrites following place field induction.

a Experimental setup. ASAP3, mRuby3 and bReaChes plasmids were single-cell electroporated in CA1 pyramidal cells. Place fields were optogenetically induced with 1s-long LED photostimulation of bReaChes at randomly chosen, fixed location on the treadmill belt for five consecutive laps. b Example tuning maps of dendrites from a non-induced (non-place) and an induced (place) cell, sorted by tuning curve maximum. c Mean normalized DE tuning vectors from an example non-induced (non-place) and an induced ('place') cell. Each arrow represents a single dendrite. d Tuning diversity across the dendritic arbor (σ_arbor) in induced (N = 15) and non-induced (N = 7) cells. Top: The dendritic arbor of induced cells exhibit significantly less tuning diversity σ_arbor, defined as the circular standard deviation of tuning peaks in the arbor, compared to the dendrites of induced cells (two-sided Mann–Whitney U test, p = 8 × 10⁻⁵). Bottom: Relationship between arbor tuning diversity and strength of somatic tuning. The arbors of induced cells exhibit low diversity at all somatic tuning strengths, while a significant inverse relationship exists between tuning diversity and soma tuning strength in non-induced cells (r² = 0.74, p = 0.006). Box: Q1, Q2, Q3; whiskers: range excluding outliers. e Relationship between tuning parameters (tuning peak, tuning strength) at the level of individual soma-dendrite pairs in non-induced (N = 7) and induced (N = 15) cells. Top row: Dendrite peak locations are tightly coupled to their corresponding soma peak location (r² = 0.95 for the line y = x, black dashed line; N = 123 dendrites from 15 non-induced cells) in induced cells but much less coherent (r² = −0.63, N = 217 dendrites from 7 cells) in non-induced cells. Bottom row: More strongly tuned somas tend to have dendrites with more spatially coherent firing in both non-induced (r² = −0.22) and induced (r² = 0.44) cells, with a higher magnitude correlation for induced compared to non-induced cells. Regression fit line is shown with bootstrapped 95% CI.

Discussion

A fundamental question in neuroscience is how spatially and temporally structured electrical activity within the nervous system gives rise to animal behavior—and conversely, how behavior in turn shapes the activity of neural circuits. In this work, we optically interrogated subthreshold and suprathreshold electrical activity across multiple behavior states and network oscillations characterizing voltage dynamics at multiple sites across the somato-dendritic membrane surface of principal cells in the hippocampus. Our results reveal dynamic compartmentalization of electrical signals in CA1PC dendrites, consistent with behavioral state-dependent differences in synaptic input structure and active dendritic integration^24,42.

Our work offers new insights into the relationship between intracellular electrical signaling and population patterns across brain states. First, we find that dendrites across subcellular domains undergo prominent network state-dependent activity modulation, in which locomotion is associated with a reduced rate of DEs. While previous calcium imaging and extracellular electrophysiological recordings reported an increase in firing rate of CA1PCs during locomotion^59,60, our result is consistent with intracellular recordings showing somatic hyperpolarization and suppressed firing rate in CA1^61–63, CA3^64,65, and CA2⁶⁵ PCs during locomotion, as well as with recent optical voltage recordings from CA1PCs²⁶.

Second, our results answer the long-standing question of whether dendrites of CA1PCs exhibit morphologically structured oscillatory dynamics in vivo. The prominent gradient in intracellular theta phase along the basal-tuft axis we find during online locomotion suggests that phase-shifted extracellular theta currents carried by extrinsic inputs to CA1^8,66,67 map onto dendrites of CA1PCs in their corresponding layer. By modulating the intrinsic excitability of dendrites⁶⁸, spatially structured membrane potential oscillations effectively serve as a clock to pace the integration of synaptic inputs and generate dendritic DEs through coincidence detection between subthreshold membrane potential depolarization and synaptic input with a significant degree of autonomy from the soma. Our finding of opposite-sign theta phase shifts for segments in the basal and oblique domains at comparable distances from the soma suggests the sub- and suprathreshold phase shifts observed cannot simply be explained by propagation delays, but may reflect anatomical gradients in the distributions of excitatory and inhibitory inputs. The observed intracellular theta gradient along the basal-apical axis is reminiscent of previous extracellular LFP recordings demonstrating that theta oscillations are organized as traveling waves in CA1^69,70. The subcellular correlates of theta oscillations we report here provide in vivo support for soma-dendrite or oscillatory interference models for the generation of the hippocampal temporal code during spatial navigation^{32,63,71–77}.

Third, our results identify subthreshold membrane potential hyperpolarization and depolarizing event rate suppression across the somato-dendritic membrane during offline SWRs. This result is in agreement with the prominent hyperpolarization observed around SWRs with somatic intracellular electrophysiological recordings from CA1PCs in vivo^78–81, (cf. ref. ⁸²). It is important to note, however, that SWRs are associated with a relative but not absolute inhibitory state for dendrites, as DEs still occur, albeit at a lower rate, around SWRs. Sharp-wave ripples are closely associated with hippocampal replay, during which online sequences are recapitulated in the offline state⁷. Inhibition can thus play a crucial role in organizing SWR-associated replay of online activity patterns while also suppressing the reactivation of irrelevant representations⁸³. The predominant dendritic inhibition in SWRs is likely brought about by GABAergic interneurons innervating CA1PC dendrites^11,84, further implicating dendritic inhibition in structuring excitatory input integration and plasticity in vivo^{35,58,78,85–87}. In particular, parvalbumin-expressing basket and bistratified cells, which are strongly activated during SWRs^11,84,88 may provide inhibition to perisomatic and proximal dendritic compartments of CA1PCs during SWRs, respectively.

Finally, our voltage recordings suggest the presence of distributed feature selectivity of electrical signals in dendritic arbor in un-tuned CA1PCs, where spatially tuned branch-level compartments tiling space exhibit a high degree of within-branch coherence even in the absence of tuned somatic output. This finding is in line with recent two-photon calcium imaging studies showing functional independence and compartmentalization in CA1PC dendrites^20,25. Recent studies also revealed that arbitrary somatic place fields can be induced in non-place cells using spatially localized electrical^33,57 or optogenetic simulation^25,38,58,89. Indeed, we find that following optogenetic field induction, dendritic tuning becomes significantly more coherent with somatic tuning in all compartments, likely due to backpropagating axo-somatic action potentials dominating dendritic tuning. Thus, similar to neocortical principal cells^14,22,23,90, hippocampal place cells may also integrate distributed input-level tuning into a singular output-level receptive field through synaptic⁵⁷ or intrinsic⁹¹ plasticity.

There are limitations to our study. The sequential two-photon imaging approach used here does not allow for disambiguation of backpropagating action potentials from locally generated dendritic spikes, or detailed characterization of propagation-dependent changes in event amplitude and shape. Furthermore, our study focuses primarily on single spikes, without resolving high-frequency complex spikes and plateau-burst events, which are more prevalent during place fields of place cells^33,60. While ASAP3 improves upon previous indicators in fluorescence-voltage response as well as tolerability in vivo, the duration of imaging is limited by bleaching considerations, which constrained our ability to capture functional tuning profiles. Genetically encoded voltage indicators have proliferated, pushing forward optical access to neural membrane potential dynamics^28,29. Newer-generation indicators are constantly being reported,^89,92–96, with continual improvements to parameters such as signal-to-noise ratio, photostability, cytotoxicity, and speed. Future work may take advantage of these improvements to record across subcellular compartments for longer trials as well as longitudinally across days, which will allow an examination of how dendritic representations evolve over longer timescales. Finally, we recorded LFP from the contralateral hemisphere, consistent with established practice, to reduce artifacts and circumvent the difficulty of recording ipsilaterally^40,88,97. Previous studies^45,46 have found high coherence in interhemispheric LFP, with highly correlated theta power, only minor ( < 20 deg) theta phase variance, as well as highly correlated SWR power and co-occurrence of events between hemispheres, though the coherence between hemispheres is not perfect.

In summary, we have illustrated how the dendritic arbor functionally compartmentalizes electrical signaling in vivo. We have shown across network and behavior states that local events are coupled to local oscillations. Our results suggest that the functional architecture of neuronal input-output transformation in CA1PCs in vivo is best captured as a multi-layer interaction between dendritic subunits exhibiting considerable autonomy, as previously suggested by in vitro and modeling studies^{24,42,98–101}. This highlights the insufficiency of point-neuron models in capturing the computational capacity of either single cells or neural circuits in vivo. While our recording configuration did not allow for simultaneous recordings from the soma and dendrite, our findings are suggestive of an important compartmentalized component of electrical signaling, in particular during theta-associated memory encoding, which could increase dendritic computational capacity in vivo^34,102–107. Future studies using simultaneous multi-compartmental recordings from place cells will aid in uncovering how dendritic oscillatory and spiking dynamics are utilized to implement the hippocampal time and rate code for navigation and learning^{32,57,72,73,108–110}.

Methods

Mice

All experiments were conducted in accordance with National Institute of Health guidelines and with the approval of the Columbia University Institutional Animal Care and Use Committee. C57Bl/6J non-transgenic mice were used for all experiments. Mice were kept in the vivarium on a reversed 12-h light-dark cycle and were housed with 3–5 mice per cage (temperature, 22-23 °C; humidity, 40%).

Cannula implants

Imaging and single-cell electroporation cannulas, having a trapezoidal shape when viewed from the side (height 1.9 mm, top length 6.6 mm, base length 3.1 mm, width 3.0 mm), were 3D printed using 316L stainless steel (InterPRO Additive Manufacturing Group, US). Glass windows of 3.0 mm diameter and 0.13-0.16 mm thickness containing a rectangular opening of 0.2 mm by 0.35 mm offset 0.3 mm from the window center were laser cut (Potomac Photonics, US) and attached to the metal cannulas using a UV-curable adhesive (Norland optical adhesive 81, Thorlabs, US). Finally, a 0.02 mm thick silicone membrane covering the rectangular opening was glued to the glass bottom using a thin layer of UV-curable silicone adhesive (5091 Nuva-SIL, Loctite, US). This allowed glass microelectrodes to easily pierce through the membrane, repeatedly, while the brain remained insulated from the environment. Cannulas were sterilized prior to implantation.

Surgery

Male and female C57BL/6J mice of 2–2.5 months of age were anesthetized with isoflurane and placed in a heated stereotactic mount where anesthesia was maintained during the surgical procedure. Eyes were lubricated (Puralube ophthalmic ointment, Dechra, US) and the scalp was thoroughly disinfected by three alternating wipes between 70% ethanol and povidone iodine solution. Meloxicam and bupivacaine were administered subcutaneously to minimize discomfort. The scalp was removed and the exposed skull was cleaned with 70% ethanol and dried with an air duster jet. The skin surrounding the surgery site was reattached to the skull using a tissue adhesive (Vetbond, 3M, US), while the skull surface was treated with a UV-curable adhesive (Optibond, Kerr, US) to improve dental cement adhesion.

For measurement of local field potential (LFP), a reference screw with a soldered lead was inserted to make contact with the contralateral-to-imaging cerebellar lobe, while a ground screw was similarly inserted in the ipsilateral-to-imaging cerebellar lobe. The insertion sites were dried and both screws were subsequently secured with dental cement. A small craniotomy matching the shape of the implantation cannula was made to center the imaging window at -2.3 mm AP, 1.6 mm ML. After removing the bone and dura, cortical aspiration was performed while irrigating the site with ice-cold cortex buffer to carefully expose medio-lateral axonal (ML) fibers overlying the hippocampus. These fibers could be visually separated into thicker and thinner types, the latter lying right above the anterior-posterior (AP) fibers. Thicker ML fibers were removed without disturbing AP fibers and the cannula was inserted and pushed down 1.6 mm, flush with the exposed tissue. The surgical site was dried and the cannula was initially glued to the bone using a tissue adhesive (Vetbond, 3M, US). Hippocampal LFP was measured by inserting a 0.004" outer ϕ PFA-coated tungsten wire (#795500, A-M Systems, US) 1.1 mm deep from dura at same coordinates as the center of the imaging window in the contralateral-to-imaging hemisphere. In a subset of implants, the recording location of the tungsten wire was determined to be within the pyramidal layer from the shape of spontaneous ripples occurring at rest in the awake mouse. The cannula and LFP wire were fixed firmly with dental cement, which covered the skull and a headbar used for head-fixation during electroporation and imaging was attached. Ground, reference and LFP signal leads were attached to a connector strip socket (851-43-050-10-001000, Mill-Max manufacturing Corp., US) similarly fixed with dental cement. Finally, saline and buprenorphine were administered subcutaneously to minimize post-operative discomfort and the well-being of mice was monitored every 12 hours for three days. Mice were left to recover for 7 days prior to the start of treadmill habituation and the implant was left to stabilize for 3 weeks before electroporation and imaging.

Single-cell electroporation

Endotoxin-free plasmids were purified using silica columns (NucleoBond Xtra Midi EF, Macherey-Nagel/Takara Bio, US). Plasmids expressing red fluorescent protein mRuby3³⁹ at 25–100 ng/μL under CAG promoter in combination with ASAP3²⁷ voltage sensor at 30–100 ng/μL under either CAG, EF1a or hSyn1 promoters, were electroporated in single dorsal hippocampal CA1-area pyramidal neurons under two-photon microscopy guidance using mice of <4 months of age at the time of electroporation.

Long-taper pipettes were pulled from borosilicate glass (G200-3, Warner Instruments, MA, 2.0 mm OD, 1.16 mm ID) using a horizontal puller (DMZ puller, Zeitz Instrumente Vertriebs GmbH, Germany) to yield a series resistance of 4-6 MΩ when dipped in 0.1 M PBS and filled with the following plasmid carrier saline solution (in mM): 155 K-gluconate, 10 KCl, 10 HEPES, 4 KOH, 0.166 Alexa488-hydrazide, having pH 7.3 at 25 degrees Celsius.

For the electroporation procedure, mice were placed in a heated, head-bar fixation equipped Zeiss stereo-microscope, and were anesthetized for  ≈ 45 min by subcutaneous injection of a Ketamine-Xylazine mixture. The dental-cement head-cap implant, cannula, imaging window and the silicone-membrane covered opening were thoroughly cleaned with sterile 0.1 M PBS and debris was removed from the opening surface using the sharp tip of an injection needle (without piercing the membrane). A custom-designed electroporator relay unit was used to flexibly switch between a patch-clamp amplifier (BVC-700A, Dagan Corporation, MN, US) head-stage used to monitor pipette resistance and a digitally-gated stimulus isolator (ISO-Flex, A.M.P.I, Israel) used to deliver electroporating voltage pulses. Both the patch-clamp amplifier and the stimulus isolator were controlled by a digitizer (Digidata 1550B, Molecular Devices, CA, US). Pipettes containing plasmid and saline solution mix were mounted on a micromanipulator (PatchStar, Scientifica, UK) and advanced at an angle of 32 degrees through the silicone membrane under two-photon laser scanning microscopy guidance using 920 nm excitation, with 80-120 mBar positive pressure until the membrane was pierced. If pipettes pierced the membrane without becoming clogged, they were advanced several 10’s of micrometers into the tissue and the pressure was reduced promptly to 20–30 mBar to avoid spilling dye under the imaging window. More frequently, pipettes were clogged on the first piercing attempt and this was usually remedied by retracting the pipette and returning it into the saline-filled bath and applying large positive pressure alone or in combination with large voltage pulses −90 V, 100 Hz, 0.5 ms pulse ON for 1 second. After unclogging, pipettes were pushed back through the silicone membrane along the same piercing tract, and the unclogging procedure was repeated usually less than three times, as needed. After each piercing, the silicone membrane resealed and in this manner could be pierced repeatedly without losing its integrity or sterile insulation within our experimental conditions. After successfully piercing the silicone membrane, pipettes were gradually advanced toward the dorsal hippocampal CA1-area pyramidal layer, at about 120-150 μm beneath the imaging window, maintaining 20-30 mBar positive pressure. Upon approaching a cell body and pipette series resistance increasing 1-2 MΩ, the pressure was decreased to 6-8 mBar and a series of −4 to −5 V, 100 Hz, 0.5 ms electroporating pulses were delivered for 1 s after which the pipette was kept on the cell body for an additional 4-5 seconds before slowly retracting. Successful electroporation was accompanied by dye filling the cell body and dendrites, with 4/5 cells remaining intact 10-15 minutes post-SCE. Out of these intact cells, a further  ≈ 4/5 cells expressed both plasmids 15-24h post-SCE, with a remaining cells usually being intact and containing residual Alexa 488. Expression of mRuby3 could be seen as early as 15h post SCE, while ASAP3 expression was evident after 24h, when Alexa488 cleared from the cell. On rare occasions only one of the plasmids was expressed. While expression levels could be varied by the choice of promoter, cell filling time, plasmid concentration and expression time, the probabilistic nature of expression introduced variability that was offset by either advancing or delaying the imaging session up to 12h. Per electroporation session, 1–2 cells were prepared in this manner, spaced 100–150 μm apart to allow for unequivocal morphological reconstruction of their dendritic trees.

Functional imaging

Head-fixed mice were habituated to run freely on a cued treadmill. Cells were imaged within 36–60h post-SCE, with plasmid-expressing cells remaining healthy for  ≈72 h post-SCE as judged by their morphology and presence of depolarizing fluorescence transients. Two-photon laser scanning microscopy was done with a custom built 8 KHz resonant galvanometer-based microscope using: a 4.0 mm 1/e² ϕ Gaussian beam aperture 3-galvo scanner unit (RMR Scanner, Vidriotech, US), 50.0 mm FL scan lens (SL502P2, Thorlabs, US) 200.0 mm effective FL tube lens (2x AC508-400-C Thorlabs, US, mounted in a Plössl configuration, custom large aperture fluorescence collection optics (primary dichroic: 45.0 × 65.0 × 3.0 mm T865lpxrxt Chroma, US; secondary dichroic: 52.0 × 72.0 × 3.0 mm FF560-FDi02-t3 Semrock, US; green emission filter: 50.8 mm ϕ FF01-520/70 Semrock, US; red emission filter: 50.8 mm ϕ FF01-650/150 Semrock, US; GaAsP PMTs for green and red channels, PMT2101 Thorlabs, US) matched to a 0.8 NA, 3 mm W.D., water-immersion Nikon 16x objective, commercial software (ScanImage, Vidriotech, US) and electronics (PXIe-1073 5-slot PXIe chassis, PXIe-7961R FlexRIO FPGA module, 5732 2-channel 80 MS/s FlexRIO DAQ, PXIe-6341 X Series DAQ, National Instruments, US). To reduce out-of-focus movement, the point spread function was axially elongated by under-filling the objective to 0.4 effective N.A. Two-photon excitation of ASAP3/mRuby3 pair was done at 960 nm (to excite mRuby3 better) using a tunable ultrafast pulsed laser source (Chameleon Ultra II, Coherent, US), modulated by a Pockels cell synced to the resonant scanning system (350-80LA modulator, 320RM driver, Conoptics, US). Transform-limited pulses were obtained at the sample using a custom SF11 glass prism-based pulse compressor.

Fluorescence scans lasting 45 seconds were acquired at  ≈ 440 Hz (50–60× optical zoom, 32 lines/frame, 32–64 pixels/line) from preselected locations on the cell body and dendritic tree (basal, apical trunk, oblique, tuft) at various laser powers to obtain a more reproducible laser power delivery that is less dependent on the imaging depth, which bleached ASAP3 fluorescence 0.3 to 0.5 of its initial value. Under these conditions no signs of photodamage were observed (e.g. beading/swelling of dendrites), cells remained healthy throughout the recordings and morphology could be recovered.

Single-cell optogenetic place field induction

Optogenetic place field inductions were performed as previously described^25,58. DNA plasmid constructs (pCAGGS-ASAP3b, pCAGGS-mRuby3, pCAGGS-bReaChes) were diluted to 50ng/μL and electroporated into single dorsal hippocampal CA1-area pyramidal neurons. Successfully electroporated cells were imaged 48-72h post electroporation. Cells were stimulated for 1 second at a randomly chosen location for five laps with an ultrafast and high-power (30-40mW measured after the objective) collimated LED at 630 nm (Prizmatix, 630 nm). LED stimulation light pulses were delivered using custom-built electronics, which were synchronized with the blanking signal of the imaging beam Pockels cell, allowing pulsed LED stimulation during the flyback periods of the Y-galvanometer between each imaging frame. Following this wide-field optical stimulation protocol, the remainder of the imaging session was used to acquire postinduction somatic and dendritic data.

Morphological reconstruction

Morphology acquisition was done using 1030 nm two-photon excitation of mRuby3, overfilling the Nikon 16x objective for 0.8 effective NA. Multiple image stacks tiling a cell were acquired at 1.0 μm axial and 0.4 μm transverse pixel resolution under isoflurane anesthesia. Neuronal morphologies were reconstructed from fluorescence stacks using Neurolucida (MBF Bioscience, US). Neurite thickness was set to full-width half-maximum (FWHM) of a fluorescent segment cross-section. Morphological path-distance measurements e.g. between imaged ROIs and the somatic compartment were done using NEURON’s¹¹¹ inbuilt functionality using custom Python scripts.

Phylogram rendering

We introduce the phylogenetic dendrogram, or “phylogram”, as a systematic visualization tool for dendritic morphology. This visualization is motivated both aesthetically and algorithmically by the tree of life visualization used in phylogenetics.

In brief, a tree data structure is constructed with the soma at the root ("last common ancestor” in phylogenetic terms). Intermediate nodes are added corresponding to branching points, with radial edge lengths proportional to physical distances along the dendrite and thickness optionally proportional to dendritic diameter. Leaf nodes correspond to dendritic tips. Finally, colored points are added to the phylogram corresponding to recorded locations. The tree is then laid out in polar coordinates.

The phylogram provides a schematic, programmatically generated way of visualizing dendritic morphology in 2D. Unlike a 2D projection view, the phylogram avoids ambiguities from self-intersections and faithfully represents distances. In addition to representing dendritic topology, distances can be measured directly as the radial distance from the soma to a recording location; angular distance is simply used to separate distinct branches.

Code for phylogram rendering was written using the BioPython, Matplotlib, and PlotLy packages.

Fluorescence signal processing and event detection

Frame scans were in-plane motion corrected and fluorescence from segmented regions of interest (ROIs) was extracted using a modified version of SIMA package¹¹². Rather than using an arbitrary scaled fluorescence signal, the modification allowed for converting fluorescence signals to a Poisson shot-noise equivalent number of detected photons. Since the speed of resonant galvanometers is not uniform, to maintain a faithful geometric representation of the sample, pixels across the scanfield are sampled unevenly in terms of the number of digitizer samples that are summed together. With the number of digitizer samples per pixel across the scanfield provided by ScanImage, an average fluorescence signal per digitizer sample (every 12.5 ns) per ROI patch was calculated. This value was converted to photon counts using previously calibrated shot-noise equivalent counts that were measured in Alexa-488 fluorescent-dye-containing solution at varying laser powers and fluorescence signal levels. Since mRuby3 red-fluorescent protein has a small but not negligible bleedthrough in the green channel, this contribution to the green channel signal was linearly unmixed and subtracted based on a previously calibrated mRuby3 only labeled cell under the same imaging conditions. To correct for bleaching, instead of fitting multi-exponential curves to ASAP3 and mRuby3 fluorescence traces, we opted for a more robust approach. Fluorescence traces were corrected by fitting and normalizing to a natural cubic spline curve having 10 knots that were geometrically spaced over 45s of recording (knots closer to each other at the start of the recording).

The modifications applied to SIMA also allowed for a frame-by-frame extraction of X- and Y-axis pixel displacement, which together with a low-pass filtered version of mRuby3 control signal (natural cubic spline with 20 ms knot intervals), were used to perform a 4th order polynomial feature multivariate regression (Scikit learn Python package¹¹³) and subtraction of ASAP3 movement-induced artifacts. If movement artifacts were too large, here defined as a decrease in mRuby3 fluorescence to less than 50% of its bleaching normalized baseline with a z-score more negative than -3, ASAP3 and mRuby3 fluorescence signals were blanked and excluded from analysis.

Depolarizing events (DEs) were detected using a thresholded match-filtered approach that was applied to the motion stabilized and high-pass filtered ASAP3 signal (butterworth, 4th order zero-phase, 0.2 Hz cutoff). The matched-filter template was constructed by averaging 440 Hz downsampled ASAP3 fluorescence responses obtained from the 4-state Markov model (see Methods: ASAP3 Markov model) in response to in vivo whole-cell soma recorded single action potential waveforms in mouse hippocampal CA1-area pyramidal neurons. DE match-filtered signal threshold for each recording was chosen by generating a Poisson shot-noise equivalent fluorescence signal and calculating a level that yielded a false positive rate in the simulation of 0.01 Hz. To avoid subthreshold changes in the membrane potential being registered as DEs, for the match-filtered signal, a minimum 5% fluorescence-change threshold corresponding to sodium current inflection point of APs was set for dendritic recordings, while for somatic recordings, due to larger fluorescence background, this was adjusted for each cell and ranged 1%-5%. To improve DE estimation, the thresholded match-filtered signal was subjected to a peak detection algorithm that pruned DE events within a 40 ms window to keep a single largest event. This parameter was chosen as the shortest value balancing the competing objectives of temporal resolution (shorter windows better) and reliability (longer windows better), and cross-validated across different sizes, with good agreement apart from very short (sub-10 sample) window sizes (Fig. S5). DEs were considered to be isolated if 45 ms before or after the event there were no other events.

ASAP3 response characterization

A comprehensive characterization of the biophysical and electrophysiological properties of ASAP3 in vitro and in vivo is reported in²⁷. We use HEK293 cells for calibration of the voltage-fluorescence response: given a ground-truth voltage waveform, we sought to measure the corresponding fluorescence signal and use it to both construct a fluorescence template for AP-like events as well as to calibrate a voltage-fluorescence response model. ASAP3 construct was cloned in pcDNA3.1/Puro-CAG plasmid backbone and used to transfect HEK293 cells with Lipofectamine 3000 (ThermoFisher, US) using 400 ng DNA, 0.8 μL P3000 reagent and 0.8 μL Lipofectamine. HEK293A cells were obtained from Thermo Fisher (mycoplasma free, not authenticated further).Cells were patch-clamped at 22–23 °C and at 37 °C after 24h from transfection using a Multiclamp 700B amplifier (Molecular Devices, US) and either voltage stepped for 1s starting from a holding potential of -70 mV to voltages between -200 and +120 mV and back or voltage-clamped using in vivo somatic measured mouse hippocampal CA1-area pyramidal neuron action-potential burst waveforms. Simultaneous with voltage stepping, ASAP3 fluorescence was excited using UHP-Mic-LED-460 LED (Prizmatix, US) through a 484/15-nm excitation filter and cells were imaged using a fast iXon 860 EMCCD camera (Oxford Instruments, US) at a frame rate of 2.5 KHz. Steady-state ASAP3 fluorescence responses were described well by sigmoidal functions (Table S1), while dynamic step responses could be fit well to single and double exponential kinetics (Table S2).

The use of voltage clamp with a ground-truth AP waveform reduces dependence on the electrophysiological properties of the cell used for calibration; the fluorescence response in culture will be comparable to the fluorescence response in vivo assuming only that the dynamics of the sensor are comparable and that the sensor is expressed similarly in both preparations.

ASAP3 Markov model

A minimal 4-state linear chain Markov gating model formalism was used that was similar to previous descriptions of ion-channel gating¹¹⁴, except that in the case of ASAP3, instead of modeling current conduction, the ensemble fluorescence brightness was modeled. To describe voltage-dependent transition rates between any two states, a linear thermodynamic model was used:

$$r\left(V\right)=r_0{e}^{-\left(a+bV\right)/\left(RT\right)}$$ 1

where r₀, a and b are transition-dependent constants, V is the membrane potential, R is the universal gas constant and T is temperature. The 4-state linear-chain voltage-dependent Markov model transition matrix was then:

$$Q\left(V\right)=\left(\begin{array}{cccc}-{\alpha }_{12}\left(V\right)\hfill & \hfill {\alpha }_{12}\left(V\right)& \hfill 0\hfill & 0\hfill \\ {\beta }_{21}\left(V\right)\hfill & \hfill -{\alpha }_{23}\left(V\right)-{\beta }_{21}\left(V\right)& \hfill {\alpha }_{23}\left(V\right)\hfill & 0\hfill \\ 0\hfill & \hfill {\beta }_{32}\left(V\right)& \hfill -{\alpha }_{34}\left(V\right)-{\beta }_{32}\left(V\right)\hfill & {\alpha }_{34}\left(V\right)\hfill \\ 0\hfill & \hfill 0& \hfill {\beta }_{43}\left(V\right)\hfill & -{\beta }_{43}\left(V\right)\hfill \end{array}\right)$$ 2

where α_ij(V) and β_ij(V) are voltage-dependent transition rates from state i to j and back respectively. The temporal evolution of the state probability vector $\overline{\pi }$ is given by:

$$\frac{\mathrm{d}\overline{\pi }}{\mathrm{d}t}=\overline{\pi }Q\left(V\right)$$ 3

which can be numerically calculated at each time-step Δt:

$$\overline{\pi }\left(t+\mathrm{\Delta }t\right)=e^{\overline{\pi }\left(t\right)Q\left(V\right)}$$ 4

To obtain the steady state probability vector ${\overline{\pi }}_{\infty }$, the following equations were solved algebraically:

$$\overline{\pi }Q\left(V\right)=0,\sum _i{\pi }_i=1$$ 5

Time-dependent ensemble fluorescence for state brightness vector $\overline{\lambda }$ was calculated as

$$F\left(t\right)=\overline{\pi }\left(t\right)\cdot \overline{\lambda }$$ 6

The 4-state linear-chain Markov model parameters were fit to the steady state and voltage step responses of ASAP3 in voltage-clamped HEK293 cells at 22–23 °C and 37 °C (Tables S1, S2) using boundary constrained limited-memory BFGS algorithm (L-BFGS-B) implemented by the Python SciPy optimization package.

Simulation of domain-specific average DE waveforms

To obtain average domain-specific DE waveforms, as shown in (Fig. 1e), in response to somatically recorded APs in vivo, single APs were isolated from adult mouse dorsal hippocampal CA1PCs whole-cell current-clamp recordings that were kindly provided by Dr. Jeffrey C. Magee (Baylor CM, TX) from ref. ⁵⁷ (baseline=-58.2 ± 0.6 mV, amplitude=93.1 ± 1.0 mV, FWHM=1.2 ± 0.0 ms, mean ± SEM). AP waveforms sampled at 20 KHz were converted to fluorescence responses using the above ASAP3 Markov model and downsampled to 440 Hz to match the imaging frame rate. Poisson shot-noise limited fluorescence waveforms corresponding to single isolated APs were generated by randomly picking DE fluorescence baseline photon counts from the distribution of measured DE baselines corresponding to each domain and applying a minimum 100 cts/sample threshold. Matched-filter event detection and averaging was done similar to the measured fluorescence waveforms.

Local field potential (LFP) measurement and preprocessing

Hippocampal LFP was measured by inserting a shielded 18-pin electrode adapter board for headstages (C3418, Intan Technologies, US) in the surgically-fixed connector strip carrying LFP signal, ground and reference. To this adapter board, an RHD2132 16-channel amplifier with ground and reference pins disconnected from each other (C3334, Intan Technologies) was attached. LFP measurement was done using an RHD2000 interface board (C3100, Intan Technologies, US) that simultaneously recorded laser-scanning frame trigger and treadmill synchronization signals at a sampling rate of 10 KHz. LFP and treadmill position signals were resampled offline to about 440 Hz (and in a few cases 220 Hz) in sync with the acquired frames.

Behavioral state classification

Behavior of mice was defined by their locomotion activity on a treadmill with tactile cues. The 2-m long cue-rich fabric belt was constructed by stitching together 3 fabrics and then adhering local tactile cues (e.g., velcro, glue gun spikes, silver glitter masking tape, green pom poms). If movement velocity dropped below a threshold of 2 mm/s for at least 1 second, mice were considered at rest. Walking/running epochs were defined to have a sustained velocity above 10 mm/s for at least 1 second.

DE rate estimation

DE rate is estimated by counting the total number of events in a behavior state (running or nonrunning) and dividing by the duration in that state. For the purposes of rate estimation, all scans from a single segment are concatenated and only epochs of at least 1 second in duration are included.

Analysis of theta-band dendritic fluorescence oscillations

Theta-band LFP phase was determined by first applying a zero-phase 20th total order 5-10 Hz Butterworth filter, assigning a phase of 0 deg to oscillation troughs and interpolating the phase between adjacent troughs using a linear function. Fluorescence recordings were split according to the animal’s behavior state to be either still or walking/running. To avoid bias from soma-modulated back-propagating action potentials, fluorescence samples from matched-filter detected depolarizing events were excluded within a 20 ms window centered on each event.

This process allows us to assign a theta phase to each recording sample during locomotion based on the theta-band LFP oscillation. The amplitude A and phase ϕ of the membrane potential oscillation relative to the extracellular oscillation were estimated using the discrete Fourier transform (DFT) estimator of sinusoidal parameters under additive white Gaussian noise (AWGN)^115,116

$$\widehat{A}\exp \left\{j\widehat{\varphi }\right\}=\frac{1}{N}\sum _{n=0}^{N-1}x\left[n\right]\exp \left\{-j{\omega }_{0}n\right\}=\frac{1}{N}\mathrm{DTFT}\left(x\right)$$ 7

The variance of the amplitude and phase estimates derived in this way are well-characterized

$$\mathrm{Var}\left[\widehat{A}\right]=\frac{2{\sigma }^2}{N}$$ 8

$$\mathrm{Var}\left[\widehat{\varphi }\right]=\frac{1}{N\frac{A^2}{2{\sigma }^2}}$$ 9

where σ² is the noise variance, estimated empirically as the residual variance.

Segments whose amplitude estimate was significantly greater than 0 (i.e., $\widehat{A}>1.645\sqrt{\mathrm{Var}\left[\widehat{A}\right]}$) were considered to be significantly phase modulated in V_m. The advantage of this estimator is its ability to detect modulation at any constant phase offset. If a significant modulation is detected, the phase offset (relative to the contralateral theta) is read off from the estimator. As variability in the placement of the contralateral LFP electrode could also introduce a constant phase offset, we report all phases relative to the estimated phase at the somatic/proximal basal compartment.

DE phase preference was calculated by first assigning each DE a unit modulus complex number $\exp \left\{j\varphi \right\}$, where ϕ is the phase of extracellular theta LFP oscillation at which the event occurred. The mean of these complex numbers was computed for each recording location: the argument corresponds to the estimate of the DE preferred phase, while the modulus (elsewhere called mean resultant length, MRL) corresponds to the degree of preference. We note that this method is equivalent to the DFT method if samples are observed at uniform intervals. Segments for which p < 0.05 under a Rayleigh test of DE phases were considered significantly phase-modulated in DEs.

Detection of hippocampal ripples

Ripple detection was done by: 1) applying a zero-phase 4th total order (2nd order forward and backward) 80-220 Hz Butterworth band-pass filter to LFP measured during behaviorally still periods, 2) squaring the filtered signal to calculate the instantaneous power and smoothing it using a zero-phase 4th total order 25 Hz cutoff low-pass Butterworth filter, 3) scoring the instantaneous power using Tukey’s inter-quartile range (IQR) and thresholding ripple epochs at an IQR level above 10, 4) expanding ripple epochs in both directions until the IQR score decreased below 2, 5) ignoring ripple events shorter than 15 ms and joining ripple events that are less than 15 ms apart.

Phase gradient estimation

Small variations in electrode placement could introduce random offsets to the extracellular theta phase; to mitigate this, we report all phases relative to the somatic phase, inferred by performing linear regression of the phases of significantly phase-modulated basal dendrites vs path distance for each cell; if the resulting regression is significant, we use the estimated intercept, otherwise, we take the mean phase. The relative phase determined in this way is defined as 0 and all subsequent phase estimates are reported relative to this inferred somatic phase. We show that the phase estimated this way agrees well with the true somatic phase for cells for which both were recorded.

We assessed the presence of a phase gradient in the membrane potential oscillation along the basal-tuft axis both parametrically and nonparametrically. Throughout, we use a signed soma path distance convention, i.e. basal ROIs distance is negative. To estimate the phase gradient parametrically, we performed least-squares linear regression of relative phase of significantly phase-modulated dendritic segments vs path distance to soma. To estimate the same gradient nonparametrically, we binned a complete theta cycle into 20 phase bins and performed rank-regression, regressing the rank of each segment’s soma path distance vs the phase bin corresponding to that segment’s minimum membrane potential. Pearson correlation coefficients and p-values were calculated in both instances.

Recording locations in the oblique and trunk domains have two quasi-orthogonal contributions to their soma path distance: the distance from the soma at which obliques branch off the trunk axis (axial distance) and the distance of the recording location to this origination point on the trunk (radial distance). To interrogate the relative contributions of these components to the phase gradient, the phase variable was regressed simultaneously against these two distances using the statsmodels Python package regression.linear_model.OLS function, employing an ordinary least squares method. Phase gradients within said dendritic domains were deemed to be present if the p-value associated with the regression was below 0.05.

Basal-oblique and basal-tuft dendritic domains phase span was measured as the phase difference between basal and oblique or basal and tuft dendritic domains by using either the mean phase of all recording locations within the domain, if the phase-distance regression was not significant, or the phase associated with the furthest recording location from the soma according to the regression model, if the regression model was significant.

Phase modulation of DE amplitude

In order to ask the question of whether DE amplitude was modulated by phase in the theta cycle, we performed linear-circular fits to the empirical histograms of amplitudes and phases (as phase is a circular variable). This translates to solving the least-squares problem:

$$\arg \underset{\alpha ,\beta ,\varphi }{\min }{\sum }_{i\in E}{\parallel A\left({\theta }_i\right)-\widehat{A}\left({\theta }_i;\alpha ,\beta ,\varphi \right)\parallel }_2^2$$ 10

where E represents the set of events, A(θ_i) is the empirical amplitude of event i occurring at phase θ_i, and $\widehat{A}\left(\theta ;\alpha ,\beta ,\varphi \right)=\alpha \sin \left(\theta +\varphi \right)+\beta$ for amplitude α, phase ϕ and intercept β. Fitting and significance assessment were performed using the statsmodels package in Python.

Peri-ripple depolarizing event rate

Significantly rate-modulated segments (Fig. 4a, S11a), were defined as segments which differed significantly in Poisson rate inside and outside SWRs. The following standardized Poisson rate-difference statistic of¹¹⁷

$$z=\frac{\sqrt{{\widehat{\lambda }}_{out}}-\sqrt{{\widehat{\lambda }}_{in}}}{\frac{1}{2}\sqrt{\frac{1}{N_{out}}+\frac{1}{N_{in}}}}$$ 11

was computed, where

$${\widehat{\lambda }}_i:=\frac{k_i}{N_i},i\in \left(\mathrm{in,\; out}\right)$$

i.e., the total number of events observed in a condition k_i divided by the total number of samples from that condition N_i. Significance was determined by a two-sided z-test at a significance level of α = 0.05. For subsequent analyses, all segments were used without pre-filtering for segment-level significance.

Peri-ripple depolarizing event waveforms and amplitudes

Depolarizing event waveforms inside and outside the LFP ripple epoch were calculated as an average of a 5-point moving average—ΔF/F in a  ± 100 ms window aligned to the DE event time, as determined by the previously described matched filtering approach. Event amplitudes were taken as the—ΔF/F value at the DE event time.

Peri-ripple membrane potential analysis

As LFP ripple events are brief, the membrane potential trough may actually be reached outside the ripple itself. The peri-ripple V_m trough was identified on a per-segment level as the minimum membrane potential value in the average segment  − ΔF/F waveform computed in an expanded window of the LFP SWR power peak  ± 200 ms.

Spatial tuning analysis

Spatial tuning analyses were performed on detected depolarizing events. Tuning curves were calculated by binning the track into 100 place bins and computing the average DE rate in locomotion epochs within each bin.

Dendritic spatial tuning may be single- or multi-peaked, driven by multiple distinct spatially-tuned inputs converging onto the same stretch of dendrite. We called a segment “spatially tuned” if its DE rate tuning curve differed significantly from shuffle. We took the H statistic of nonuniformity described in⁵⁵ as our base tuning metric, and discarded segments which were not significantly nonuniformly tuned to p < 0.05 under this metric. A null distribution on this statistic was constructed by randomly permuting DE times within locomotion epochs 10,000 times for each segment and calculating the H statistic on each permutation, and the 95th percentile of this distribution was chosen as the critical value for determining significance.

Circular Wasserstein distance

Distance between tuning curves (TCD) was computed using the circular Wasserstein distance, defined as in eq. (10) of ref. ⁵⁶:

$$d:=\underset{\alpha \in \mathbb{R}}{\inf }{\int }_{t\in \left[0,1\right)}\mid F-G-\alpha \mid$$ 12

where F and G are the respective cumulative density functions (normalized to unit norm), and t ∈ [0, 1) corresponds to the normalized position around the circle.

The circular Wasserstein distance (also known as earthmover’s distance or Monge-Kantorovich distance) measures the total “cost” associated with transforming one distribution into another in terms of transporting probability mass. For single-peaked distributions, this corresponds to the usual intuition of moving the “mass” of one peak to another: the further apart the peaks, the higher the cost. Unlike peak-based metrics, the Wasserstein distance is robust to multipeaked distributions.

Construction of somatic tuning curve from dendritic tuning curves

The place-cell somatic tuning curve is classically modeled as a Gaussian distribution on the circle, parameterized by an angular mean and variance. The tuning curves of spatially tuned dendrites were taken as the basis set, and we asked whether any somatic tuning curve could be approximated up to scale as a nonnegative linear combination of these basis variables. We generated circular Gaussian tuning curves for a range of μ and σ parameters and computed the mean reconstruction quality as the average Spearman’s ρ between the NNLS reconstruction and the idealized tuning curve. We compared several alternative hypotheses: the soma tuning curve only, spatially shifted copies of the soma tuning curve, and the same number of linearly independent random tuning curves as significant dendrites.

Tuning resultant vector analysis

We used tuning resultant vector analysis following⁴¹ to quantify how dendritic event tuning changed with place field induction. Briefly, every DE during locomotion was assigned a complex number corresponding to the position in which it occurred, and the resultant vector was computed as the complex mean of all of these vectors, normalized in magnitude from [0,1]. The argument (direction) of this resultant corresponds to the direction of tuning, while the magnitude corresponds to a continuous measure of the strength of tuning. Tuning variability was defined within a dendrite as the circular standard deviation of the events that occurred within that dendrite. Tuning diversity was defined across the arbor as the circular standard deviation of the resultant tuning vectors observed at all dendrites across the arbor.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

A.L. and A.N. conceived the study and wrote the manuscript; Z.L. analyzed data, wrote the manuscript; A.N. analyzed data, designed and constructed custom two-photon laser-scanning microscope with the help from D.H.; A.N. developed and applied single-cell electroporation; A.N. performed surgeries together with D.M.L.; A.N. performed experiments, preprocessed and validated data, developed ASAP3 Markov model based on data contributed by G.Z. and M.Z.L; K.C.G. performed surgeries, performed experiments and preprocessed data; C.Y. reconstructed neuronal morphologies and contributed with illustrations; D.M.L. and N.E.M. performed image analysis, segmentation, morphological registration, behavior training together with A.N.; M.C., S.W.E., J.Y., C.M., and M.Z.L. provided ASAP3 GEVI and advice. The following authors contributed equally: C.Y., D.H., N.E.M.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data generated in this study have been deposited in the Dryad database as 10.5061/dryad.8cz8w9h0h. Source data are provided with this paper.

Code availability

The software generated in this study have been deposited in the Zenodo database as 10.5281/zenodo.11215569.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-50546-z.