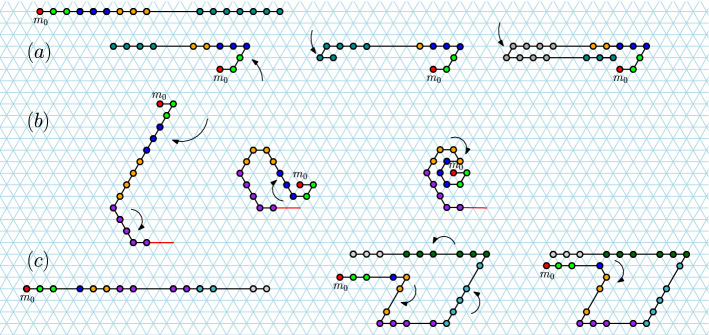
Fig. 14.

Illustration for Case 1 of the proof of Theorem 38, showing that a 2-turn, 1-gap, Spiral can not be folded from “inside to out”. Top left: initial configuration, monomers are co-linear, colours distinguish initial states. a Initial configuration with all states positive. First we fold the intended innermost coil/turn of the spiral, by rotating almost the full line of monomers anti-clockwise by $\pi$, creating a small “pocket” (red, green, and blue monomers). Then the teal/grey monomers “prematurely” fold the configuration into the pocket, eventually yielding a permanently blocked configuration—to carry out the folding it suffices that the teal monomers have initial state $\ge 6$. b Initial configuration with all states negative. The trajectory shown folds into a permanently blocked configuration similar to that in Fig. 7, but here uses clockwise turning (negative states) and has an extra long tail that needs to be folded out of the way before completing the erroneous tight spiral. The configuration in on the right is not (yet) permanently blocked, but the 7 monomers in the inner tight spiral are permanently blocked and thus all trajectories forward lead to permanently blocked configurations. c Initial configuration with strictly positive and strictly negative states. By Case 1(c) in the proof, there is a contiguous segment of monomers in state 0, here shown in purple. Monomers to the left (negative states) fold clockwise, and monomers to the right (positive states) fold anticlockwise, yielding a pincer-like permanently blocked configuration