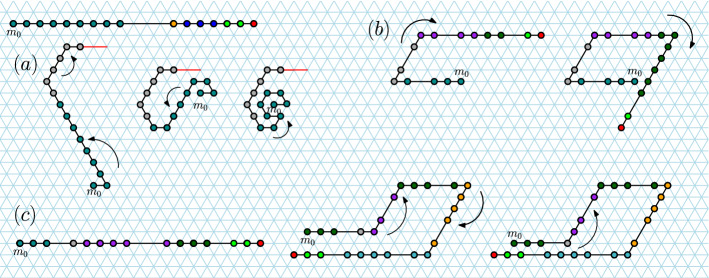
Fig. 15.

Illustration for Case 2 of the proof of Theorem 38 showing that a 2-turn, 1-gap, Spiral can not be folded from “outside to in”. Top left: initial configuration, monomers are co-linear, colours distinguish initial states. a Initial configuration with all states positive. Trajectory shown folds into a permanently blocked configuration similar to that in Figs. 14b and 7 . The configuration to the right is not yet permanently blocked, but the 7 monomers in the inner tight spiral (starting at $m_0$) are permanently blocked and thus all trajectories from this configuration will yield permanently blocked configurations. b Initial configuration with all states negative. First we fold the outer most part of the spiral by rotating almost a full line of monomers clockwise by $\pi$ creating a large “C shape” (dark green, gray, purple monomers). Then the remaining arm of the spiral folds such that it is anti-parallel to the y-axis (right). This arm of the spiral wishes to rotate clockwise to reach the center, but to do so would cause these monomers to intersect with the “C shape” outer coil of the spiral, thus leading to a permanently blocked configuration. c Initial configuration with both strictly positive and strictly negative initial states. This construction is similar to that used in Fig. 14c such that there is a contiguous segment of monomers with states $0,0,\dots ,0$, here shown in dark green. Monomers to its left (positive states) fold anti-clockwise, and monomers to the right (negative states) fold clockwise, yielding a “pincer-like” permanently blocked configuration