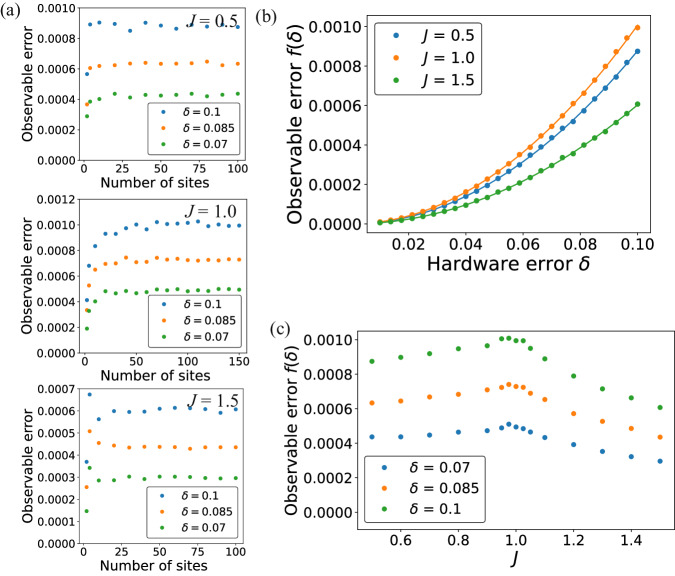
Fig. 2. Numerical study of the impact of errors in the SSH model.
The observable that we study here is O = HSSH[ J]/n, where HSSH[ J] is the Hamiltonian of the ideal SSH model (Eq. (9)) a The error in the expected value of the observable O in the ground state between the perturbed and unperturbed Hamiltonians, as a function of δ, the hardware error, and the number of sites n. For both gapped (J = 0.5, 1.5) and gapless ( J = 1.0) cases, we see that the error in O becomes independent of n as N → ∞. b Numerically extracted error between the perturbed and unperturbed models for n → ∞ as a function of δ, and its fit with δ2. c The error between the perturbed and unperturbed model as a function of J—for the same hardware error δ, this error peaks at J = 1 which is also the point at which the gap in the unperturbed model closes. All the errors are computed by averaging over 500 random instances of perturbed models.