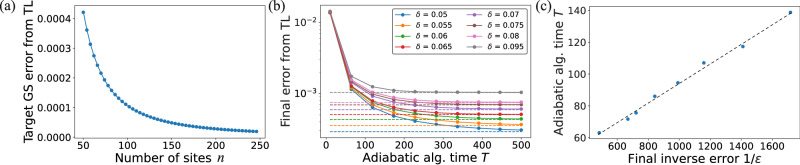
Fig. 4. Numerical study of quantum adiabatic algorithm in the presence of error.

We consider using the adiabatic algorithm to find the energy density observable for the critical SSH model in the thermodynamic limit (TL). a Convergence of the energy density to the thermodynamic limit as n → ∞—the scaling of ε with n reveals a power-law scaling that is expected for gapless models. b The adiabatic algorithm in the presence of hardware errors—the quantity being plotted is the error of the noisy adiabatic algorithm from the thermodynamic limit of the noiseless model. The precision achieved by the adiabatic algorithm is fundamentally limited by hardware errors. c The final precision (ε) achieved by an adiabatic algorithm in the presence of errors as a function of the adiabatic algorithm run-time, confirming that T ~ poly(1/ε) as expected from our analysis. Thus, on decreasing the hardware error, the error achievable by the noisy quantum simulator decreases and the run-time of the quantum algorithm increases at most polynomially.