Abstract
Synchronization in complex networks is a ubiquitous and important phenomenon with implications in various fields. Excessive synchronization may lead to undesired consequences, making desynchronization techniques essential. Exploiting the Proximal Policy Optimization algorithm, this work studies reinforcement learning-based pinning control strategies for synchronization suppression in global coupling networks and two types of irregular coupling networks: the Watts-Strogatz small-world networks and the Barabási-Albert scale-free networks. We investigate the impact of the ratio of controlled nodes and the role of key nodes selected by the LeaderRank algorithm on the performance of synchronization suppression. Numerical results demonstrate the effectiveness of the reinforcement learning-based pinning control strategy in different coupling schemes of the complex networks, revealing a critical ratio of the pinned nodes and the superior performance of a newly proposed hybrid pinning strategy. The results provide valuable insights for suppressing and optimizing network synchronization behavior efficiently.
Keywords: Reinforcement learning, Synchronization suppression, Pinning control, Complex networks
1. Introduction
Synchronization in complex networks has been emerged as an essential phenomenon and a topic of great interest in various disciplines, including physics, biology, engineering, and chemistry [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], due to its relevance to the stability and robustness of numerous real-world systems. Synchronization in ensembles of coupled oscillators is recognized as they achieving a same rhythm and has been extensively investigated. Although synchronization can be beneficial in certain scenarios [12], such as the coordination of power grids [13] and the coordinated firing of cardiac pacemaker cells [14], [15], excessive synchronization may lead to adverse effects, e.g., system collapse [16], or the emergence of undesirable collective behaviors [17], [18]. In the realm of neurological diseases, abnormal neuronal synchronization is proved to be a critical underlying factor. Usually, sufficiently strong interactions synchronize units of a network, leading to collective rhythm of the system, which is frequently detrimental and shall be suppressed. Notably, pathological synchronization within the neuronal circuits of the basal ganglia and thalamus is associated with the induction of tremors which may lead to the development of Parkinson's disease. Therefore, it is essential to understand and control undesired synchronization behavior of complex networks, ensuring the optimal performance of these systems.
In this context, Deep Brain Stimulation (DBS) has been developed to address the pathological synchronization via implanting micro-electrodes to certain regions of brain, exerting high-frequency pulse stimulations [19]. This technique for synchronization suppression utilizes explicit control signals, i.e., open-loop strategy. However, open-loop methods depend heavily on human-designed signals and suffer from external disturbances. Feedback controllers are then introduced to eliminate synchronization sustainably and efficiently [20], including the adaptive techniques [21], time delay-based techniques [1], etc. Recently, reinforcement learning (RL) is brought in to generate and adjust control signals automatically according to the system's current state [22], [23], [24], [25], [26], which achieves effective desynchronization performance. Despite advancements, there remains a need to reduce the invasiveness of control strategies theoretically and practically. Current methods, including those using reinforcement learning, apply control signals to all nodes in the network, resulting in high energy consumption and significant disturbance to the system. The primary problem addressed in this study is to develop a method that reduces the intrusion into the system while effectively suppressing undesired synchronization. One promising approach to achieve this goal is pinning control, which selectively applies control signals to a subset of nodes within the network [4], [27], [28], [29], [30]. By targeting only key nodes, pinning control aims to minimize intervention and reduce overall energy consumption. Various strategies have been proposed to identify and select these key nodes based on their importance in the network [31], [32]. Another notable approach to reducing invasiveness involves the use of precisely timed pulses to control collective synchrony in oscillatory ensembles. Rosenblum [33] introduced a method that applies stimuli only at the most sensitive phases of the oscillation cycle. This technique significantly reduces the number of pulses required, thereby minimizing system disturbance and energy consumption. By combining the principles of precisely timed pulses with pinning control, we can further enhance the efficiency and effectiveness of synchronization suppression strategies.
In this work, we study reinforcement learning-based pinning control strategies for synchronization suppression in complex networks, taking into account different network structures including global coupling networks and typical irregular coupling networks [34], [35], [31]. Implemented with the Proximal Policy Optimization (PPO) algorithm [36], several pinning strategies to select key nodes are proposed to realize desynchronization of oscillatory systems in the RL environment. We further investigate the impact of the ratio of controlled nodes and the role of key nodes selected by the LeaderRank algorithm [37], [38] on the performance of synchronization suppression in the well-known Watts-Strogatz (WS) small-world networks [39], [40], [41], [42], [43] and Barabási-Albert (BA) scale-free networks [44], [45], [46], [47], [48]. Numerical results demonstrate the effectiveness of the reinforcement learning-based pinning control strategies in different coupling schemes of the complex networks, revealing a critical ratio of the pinned nodes and the superior performance of a newly proposed hybrid pinning strategy. The results provide valuable insights for suppressing and optimizing network synchronization behavior efficiently.
The remaining part of this paper is organized as follows: Section 2 introduces several types of complex networks considered in this work, as well as the utilized strategies for controlled nodes selection and the reinforcement learning environment for control signals generation. Section 3 presents and discusses the experimental results. Section 4 summarizes the findings and concludes the work.
2. Models and methods
We first describe several types of complex networks considered in this work, which consist of coupled oscillators, as well as the utilized strategies for controlled nodes selection and the reinforcement learning environment for control signals generation. Specifically, we consider the cases of global coupling networks and typical irregular coupling networks. In the former scenario, starting from the whole, pinned nodes are randomly selected and we analyze the synchronization suppression performance when gradually decreasing their ratio in the network. While in the latter networks, LeaderRank algorithm is incorporated to pinpoint the key nodes and we evaluate the performance when varying proportions of them are controlled. In addition, a hybrid strategy is proposed to advance the overall desynchronization performance across different networks.
2.1. Global coupling networks
In networks of coupled oscillators, global coupling refers to simple circumstance that each oscillator interacts with all others (all-to-all connection or fully-connected network) [49]. Here, each node is represented by a Bonhoeffer-van der Pol (BVP) oscillator [50], whose networks are generally used to capture the essential dynamics of a wide range of oscillatory systems. Ensembles of BVP oscillators have emerged as basic tools for probing intricate phenomena, such as synchronization and desynchronization. Consider N globally coupled BVP oscillators, described by the following two-dimensional nonlinear differential equations:
| (1) |
where denotes the population of oscillators. We consider the case of heterogeneous oscillators, representing by the external stimulus sampled from a Gaussian distribution, i.e., with and . The oscillators are globally coupled through the term of their mean field with coupling strength ε. Pinned nodes will additionally receive input signals generated via reinforcement learning. BVP oscillators can exhibit rich dynamical behaviors including stable limit cycles, bistability, and chaotic dynamics, within varying regimes of parameters.
We consider oscillators and fix the coupling strength ε as 0.03 in the global coupling scenario. In these settings, our goal is to suppress the synchronization behavior of the population induced by the moderate strength of global coupling, while accounting for the variability introduced by the randomly designated . Practically, control protocols stand for external intrusions to the system and consume energy resources. Pinning strategy is then introduced to mitigate such intrusive effect by imposing signals to minor selected nodes. To be concrete, we first train a PPO agent that exerts action to every oscillator to suppress synchronization, and then gradually decrease the ratio of controlled nodes. Due to the global coupling mechanism, every node takes the same position in the network, and the selection of pinned nodes degrades to a completely random strategy, which we term as Random Pinning Strategy (RPS). This strategy is the simplest and has also been applied to control other types of complex networks.
2.2. Typical irregular coupling networks
Two typical types of irregular coupling complex networks are broadly observed in real-world scenarios and are comprehensively investigated in the past decades. Compared to global coupling networks, the irregular coupling networks endow their nodes with distinct roles in generating dynamics on them. The celebrated Barabási-Albert scale-free network is constructed from an initial small network by successively adding new nodes to it, where the new nodes tend to connect the existing ones with high degrees. This procedure results in a network with a few hubs and many low-degree nodes, leading to a power-law degree distribution. The Watts-Strogatz small-world network is built from a nearest-neighbor coupling network. At each step, a link is randomly rewired with probability p, which creates the small-world property with high clustering coefficient and low average shortest path length. Notice that corresponds to the original regular network and corresponds to a completely random network, also termed as Erdös-Rényi (ER) network.
We still employ the BVP oscillators but connecting them with certain network structures, which can be described by
| (2) |
where is a zero-one matrix denoting the specific network structure and denotes the degree of the i-th node. The heterogeneous external stimuli are the same with the setting in Section 2.1. We fix the coupling strength ε as 0.1 in this scenario and consider the generated WS small-world and BA scale-free networks with average node degree .
For oscillatory networks with nodes, we also use the PPO algorithm to first train two agents corresponding to both WS and BA networks separately, allowing the agents' actions to act on every oscillator during training. We find that under the same parameter conditions, both trained agents exhibit excellent generalization capability across the distinct WS and BA network structures. Therefore, we choose the model with better desynchronization performance to conduct the subsequent experiments. Moreover, since the nodes in irregular networks may have distinct positions in determining the desynchronization process and for the sake of minimizing pinned nodes, we sort them according to their importance in the corresponding network, which are characterized by the LeaderRank algorithm. This algorithm pinpoints the most influential and important nodes in the networks. Based on this sorting, Importance Pinning Strategy (IPS) can be introduced to select the pinned nodes with higher importance, which may contribute to better desynchronization performance but depend on the varying network structures. We will compare RPS and IPS in the following numerical examples.
We also demonstrate in the following experiments the differences in synchronization suppression process between the WS and BA networks. In fact, we observe that BA scare-free networks sometimes suffer from less effective performance in synchronization suppression with RPS or IPS, while maintaining an acceptable small ratio of controlled nodes. To accommodate such situations, we propose a Hybrid Pinning Strategy (HPS) which determines the pinned nodes via trading off the ones selected by RPS and IPS, integrating both node importance and randomness.
2.3. Reinforcement learning environment
Reinforcement learning (RL) is a machine learning paradigm that involves the interaction between an agent and its environment, wherein the agent performs actions that affect the state of the environment. This change in state results in a corresponding reward signal, which can be either positive or negative. The agent then formulates subsequent actions based on its current state and the reward it received, typically guided by a policy. In this setting, the objective of RL is to devise a policy that maximizes the cumulative reward garnered through the agent's actions over time. Here, in the context of suppressing the synchronization of networked BVP oscillators, we employ the RL environment used in the seminal works [24], [22], which is described in the following.
2.3.1. Action and state
In our setting, the action and the state can simply represent the input to and the resulting output from the environment (i.e., the oscillatory system), sampled at a time interval of Δ. Idealistic δ-shaped pulse actions with constant interpulse interval Δ is considered, whose amplitude is restricted by . Therefore, the actions satisfy with . The amplitude can be tuned in RL at each time step, while small values of are encouraged to minimize the invasion to the systems, especially in the real-world context of designing deep brain stimulation for Parkinson's disease [33]. To this end, a total input “energy”, defined by , is measured, which will then be minimized during training.
The state is directly read out from the current value of the mean field , which represents the system's response after taking action . Practically, we encompass most recent values of X (denoted as ) to accommodate the oscillatory behavior of the system.
2.3.2. Reward
In our task, the reward function is expected to repress the synchronization among oscillators while penalizing excessive energy consumption or invasiveness. Therefore, the following class of reward functions is utilized:
| (3) |
where the first term rewards synchronization and the second term penalizes excessive actions, with the coefficient β serving as a trade-off between these two terms. Notice that . We set for the task in global coupling networks and for the typical irregular coupling networks.
2.3.3. Agent
The PPO algorithm is a well-known type of policy-based reinforcement learning that seeks to optimize a policy function by maximizing the expected return of actions received from the environment. PPO is characterized by its use of a clipped surrogate objective function, which can update the policy function in a way that prevents it from changing too much from one iteration to the next. This technique mitigates the risk of harmful large policy updates, thereby improving the stability and reliability during training. The PPO algorithm typically employs the Actor-Critic architecture, where the Actor is responsible for policy generation and the Critic estimates the advantage function [51]. Now the policy can be defined as:
| (4) |
Here, π represents a policy mapping from states to actions parameterized by a neural network with parameters θ, determining the action to take given a particular state. θ is then optimized using PPO to maximize the expected return with γ being the discount factor (usually set to 0.99). Notice that in the context of pinning control, the actions are taken on only a subset of nodes, and the reward should be instead calculated by summing on all these pinned nodes. Moreover, in RL the advantage function assesses the superiority of a specific action over the averaged one in a given state. In fact, it is usually performed using the current policy to sample a trajectory in the environment, including series of states, actions, and rewards, and calculate the corresponding value of the advantage function for each step. Other general PPO and RL environment and parameter configurations can be referred to [24].
2.4. Measuring the performance of desynchronization
To make fair comparisons on the desynchronization performance with different pinning strategies and various network structures, we introduce two measures: suppression coefficient and synchronization error. The extent of the mean field suppression can be quantified by the following suppression coefficient:
| (5) |
where denotes the mean field values before the application of input stimuli, while denotes the values after the stimuli application. This measure characterizes desynchronization from a macroscopic rhythm perspective. To describe desynchronization performance in detail and further avoid other factors such as amplitude death that may cause macroscopic rhythm quenching, synchronization error is introduced [52]:
| (6) |
where denotes the average over a sufficiently large time window T.
3. Results
When applying RL-based control to all nodes in a global coupling network using our pre-trained model, i.e., no pinning strategy is taken, the system's mean field is rapidly suppressed. As shown in Fig. 1(a), the required control amplitude diminishes quickly and only relatively small amplitudes are needed to maintain the desynchronization performance. However, when the control signal is switched off, the mean field gradually oscillates and the system recovers to synchronization. It is noted that although external control signals invade the system, the dynamics of individual oscillators barely change but their oscillations become incoherent (Fig. 1(b)). This is essential for the RL-based control signals to manifest their effect only on preventing the emergence of macroscopic oscillations and without disturbing individual dynamics, which facilitates real-world applications. It has been demonstrated that the mean field fluctuations in the suppressed steady state depend on the population size as [53]. However, this theoretical limit can only be strived to approximate due to noise influence practically. Pre- and post-intervention behaviors of the network are shown in Fig. 1(c).
Figure 1.
Synchronization suppression performance in a global coupling network of BVP oscillators. Here control signals are applied to all nodes in the network and coupling strength is fixed to 0.03. (a) Network mean field (X, black) and the action pulses (orange) generated for suppression. Control is switched off at time step 6000. (b) The dynamics of two randomly selected oscillators (x, black and red) demonstrate that the system achieves desynchronization without disturbing individual dynamics. (c) Pre- and post-intervention behaviors of the network plotted for 50 nodes.
In the following, we discover the RL-based pinning control strategies to further reduce control energy consumption. Concretely, we analyze the synchronization suppression performance using RPS when gradually decreasing the ratio of pinned nodes in global coupling networks, and compare RPS and IPS in typical irregular coupling networks. We apply Stable Baselines [54], an open source RL toolset, to implement our experiments. The detailed parameters and configurations used include: discount factor 0.99, entropy coefficient for the loss calculation 0.01, learning rate 0.00025, number of training minibatches per update 4, trade-off bias 0.95, the number of steps to run for each environment per update 128.
3.1. Random pinning strategy in global coupling networks
We first test whether and to what extent pinning control can be effective in an ensemble of globally coupled BVP oscillators. Fig. 2 presents the results of typical cases when the ratio of pinned nodes decreases from 100% to 20% using RPS. It is evident that the time steps required for suppressing synchronization to a steady state significantly increase as the ratio of pinned nodes decreases, and finally desynchronization can no longer be achieved. The similar phenomenon that maintaining desynchronization state requires relatively smaller control amplitudes than the initial suppressing process can also be observed here. The transition from effective desynchronization to failure suggests a more detailed investigation. To this end, we present the variations of suppression coefficient (S), synchronization error (E), and total input energy () versus the ratio of controlled nodes in Fig. 3. Interestingly, all the three curves demonstrate a abrupt change around 32% of the pinned nodes, below which desynchronization can hardly be achieved by RPS. Specifically, suppression coefficient in Fig. 3(a) characterizes this abrupt change from the macroscopic rhythm perspective, where pinning control loses its efficacy below the critical value. The synchronization error in Fig. 3(b) reveals a slow decline when the pinned nodes are gradually removed, whereas a drastic drop occurs at the critical value. The total input energy shown in Fig. 3(c) also demonstrates this transition, providing practical insights to real-world applications.
Figure 2.
Synchronization suppression performance using RPS in a global coupling network. Notice that the time steps required for suppressing synchronization to a steady state significantly increase as the ratio of pinned nodes decreases, and finally desynchronization can no longer be achieved.
Figure 3.
Variations of three measures versus the ratio of controlled nodes using RPS in a global coupling network. All the three curves, i.e., suppression coefficient (S), synchronization error (E), and total input energy (Atotal), demonstrate a abrupt change around 32% of the pinned nodes, below which desynchronization can hardly be achieved by RPS. The shaded area represents the standard deviation of the results for twenty realizations.
3.2. Random pinning strategy in typical irregular coupling networks
We further perform our RPS in two types of typical irregular coupling networks: the WS small-world networks and the BA scale-free networks, and test their desynchronization performance. To maintain consistency across the studied networks, we set and the average node degree for all generated networks.
The WS small-world networks, first introduced by Duncan J. Watts and Steven H. Strogatz in 1998, aim to capture the characteristics of many real-world networks, e.g., power networks, social networks, food chains and so on. With a relatively small rewiring probability p, WS networks exhibit high clustering coefficient and low average shortest path length. We initially set . The property of low average shortest path length in WS networks contributes to shorter information transmission paths and faster information spreading throughout the whole network, which thereby improves the efficiency of the desynchronization procedure. As shown in Fig. 4, by utilizing our RPS in the PPO algorithm, the system converges to desynchronization state within a few time steps and its performance remains outstanding when pinning control is applied to only 50% of the nodes, though the time steps required to reach a suppressed steady state become slightly longer as less nodes are pinned. However, when the control signals are switched off, the recovery procedures to synchronous state in WS networks exhibit significant inhomogeneity, even in different trails under the same experimental conditions, as depicted in Fig. 4, which may be due to the different initial states after the termination of control, the highly complex interacting relationships among nodes, and/or the various synchronizability of the systems, and will be included in our future detailed inspections.
Figure 4.
Synchronization suppression performance using RPS in a WS small-world network, where the rewiring probabilitypis set to 0.4. The system converges to desynchronization state within a few time steps and its performance remains outstanding when pinning control is applied to only 50% of the nodes.
Moreover, the rewiring probability p largely determines the property of WS small-world networks. We thus investigate how the desynchronization performance using RPS is affected by this structural parameter. For the networks with p increasing from 0 (regular network) to 1 (random network), we apply pinning control to randomly selected 50% nodes. As depicted in Fig. 5, when p is relatively low, the synchronization in WS networks can be effectively eliminated, as reflected in the low suppression coefficient S/total input energy A and high synchronization error E. However, these measures tend to move towards the direction of low but stable desynchronization efficiency as p increases, where the networks have relatively higher average shortest path length. These results also demonstrate the relationship between WS networks' synchronizability and the parameter p, and provide empirical support for the modulation of synchronous behavior in complex networks.
Figure 5.
Variations of three measures versus the rewiring probabilitypusing RPS in WS small-world networks. The shaded area represents the standard deviation of the results for twenty realizations.
When considering the BA scale-free networks, we notice that the required ratio of pinned nodes is significantly larger than the WS small-world networks with rewiring probability , as shown in the curves with RPS in Fig. 6. This also implies a larger synchronizability for the BA networks. We speculate that the performance can be improved with redesigning pinning strategy to control the hubs in BA networks.
Figure 6.
Variations of three measures versus the ratio of controlled nodes using RPS and IPS in typical irregular coupling networks. IPS and RPS have a similar performance when the number of controlled nodes exceeds 40%, both achieving good desynchronization results. Their performance differs when this number falls below 40%.
3.3. Importance pinning strategy in typical irregular coupling networks
A lot of key node detection methods in complex networks have been proposed in the past decades, such as degree centrality, eigenvector centrality, betweenness centrality and so forth. These measures characterize the importance of nodes in networks from different aspects. In our study, we employ the LeaderRank algorithm to rank the nodes, which has been proved effective to identify the influential spreaders in networks. This algorithm is a simple variant of PageRank, where a virtual “ground node” connected bidirectionally with every other node is introduced into the original network, and then the standard random walk process is applied to dig out influential spreaders [37]. LeaderRank algorithm converges faster than PageRank since the introduced ground node renders the network strongly-connected, and is more robust to noise and spammers. We exploit the LeaderRank values to sort all nodes and apply pinning control to a proportion of nodes with the highest values.
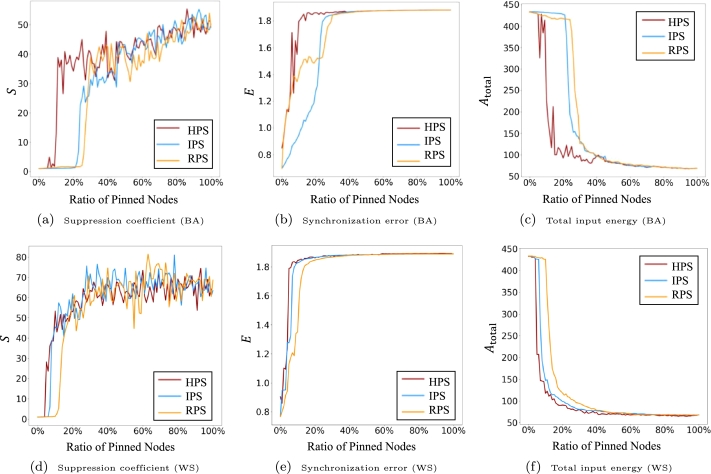
We present the synchronization suppression performance using IPS on both BA and WS networks and compare the results to using RPS. As illustrated in Fig. 6, IPS and RPS have a similar performance when the number of controlled nodes exceeds 40%, both achieving good desynchronization results. However, when this number falls below 40%, the advantages of IPS, i.e., controlling the nodes with high importance, become significant, particularly in WS small-world networks. Fig. 6(d)-(f) demonstrate this fact that in WS small-world networks, IPS achieves better desynchronization performance with lower energy consumption than RPS, under the same ratio of pinned nodes. The results in turn verify the essential role of the selected nodes, through which pinning control can achieve same effectiveness with fewer targets.
3.4. Hybrid pinning strategy in typical irregular coupling networks
It should be noted that IPS does not achieve the expected better performance compared to RPS in BA scale-free networks, as depicted in Fig. 6(a)-(c), where only the synchronization error metric expresses minor advancement. A possible reason lies in that the structure of WS small-world networks enables more long-range connections among nodes and key nodes' homogeneous roles to the network dynamics, while most nodes only link to a few hubs in BA scale-free networks and thus key nodes have distinct governed area. This difference significantly affects the desynchronization process especially when the number of controlled nodes is limited so that not all important hubs are covered in BA networks, leading to incomplete focused area of pinning control using IPS and only local desynchronization effect.
To address this problem, we further propose the Hybrid Pinning Strategy, especially for the BA scale-free networks. It determines the pinned nodes via trading off the ones selected by RPS and IPS, integrating both node importance and randomness. Here we test a scenario with a combination of 60% key nodes selected by IPS and 40% randomly selected nodes by RPS. Fig. 7(a)-(c) displays the performance of this balanced strategy and its comparison with IPS and RPS, showing a significantly improved synchronization suppression result. This strategy allows for effective and efficient synchronization suppression across various types of complex networks, providing valuable insights for suppressing and optimizing network synchronization behavior. Fig. 7(d)-(f) also demonstrate the advancement of HPS in WS small-world networks.
Figure 7.
Variations of three measures versus the ratio of controlled nodes using HPS, IPS, and RPS in BA scale-free and WS small-world networks. Notice that the proposed HPS significantly improves the desynchronization performance in both networks.
3.5. Comparison with precisely timed pulses method
We further incorporate the proposed pinning control strategies into a traditional synchronization suppression method, i.e., precisely timed pulses [33], and compare the performance with our RL-based methods. As shown in Fig. 8, HPS based on the LeaderRank algorithm significantly outperforms RPS regarding to the suppression coefficient in BA scale-free network. Remarkably, applying precisely timed pulses to only 1% of the nodes can achieve effective synchronization suppression. Despite its effectiveness, the traditional method relies heavily on predesigned and meticulously tuned controller parameters along with precise system models, whereas RL-based methods present a distinct advantage. RL learns optimal strategies through interaction with the environment, allowing it to autonomously adapt to varying system dynamics and noise conditions without precise system models. This adaptability renders RL-based synchronization suppression methods particularly flexible and effective in managing complex and dynamically evolving neural systems, offering a promising direction for future research in network control strategies.
Figure 8.

Comparison with precisely timed pulses method in BA scale-free network. The experimental settings are the same with those in Fig. 7(a).
4. Conclusion
In this study, we propose and analyze a series of reinforcement learning-based pinning control strategies for synchronization suppression in oscillatory systems coupled with several types of network structures. Specifically, in global coupling networks where all nodes take similar positions, a critical ratio of pinned nodes is discovered below which desynchronization can hardly be achieved. This abrupt change provides practical guidance in real-world applications such as DBS. In two typical irregular coupling networks, the roles of individual nodes become prominent so that pinning strategies based on the nodal importance measures are introduced and compared with randomly selection. While the strategy of pinning key nodes improves the synchronization suppression performance in WS small-world networks, our newly designed hybrid pinning strategy achieves significant advancement in BA scale-free networks.
Limitation of the current work lies in that it remains a simulation-based study whereas real-world applications require more intensive investigation. Future work of this study includes investigating the theoretical basis for RL-based pinning control, designing more efficient pinning strategies with reduced energy consumption, and further exploring the application of the developed strategies in various network settings. Our study offers detailed insights into how different network structures influence synchronization suppression and demonstrate practical techniques for effectively modulating synchronous behavior with minimal system intrusion. Our work also reveals valuable insights regarding the synchronizability of different structured networks and the practical modulation of synchronous behavior in complex networks, offering promising solutions for efficient and less invasive synchronization suppression, contributing to the broader field of network science and its real-world applications.
CRediT authorship contribution statement
Kaiwen Li: Writing – original draft, Visualization, Validation, Methodology, Investigation. Liufei Yang: Writing – review & editing, Validation. Chun Guan: Writing – review & editing, Validation, Investigation. Siyang Leng: Writing – review & editing, Visualization, Supervision, Methodology, Funding acquisition, Conceptualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 12101133). This work is also supported by Science and Technology Commission of Shanghai Municipality (No. 2021SHZDZX0103 and No. 21DZ1201402).
Data availability statement
No data was used for the research described in the article.
References
- 1.Zhou S., Lin W. Eliminating synchronization of coupled neurons adaptively by using feedback coupling with heterogeneous delays. Chaos, Interdiscip. J. Nonlinear Sci. 2021;31(2) doi: 10.1063/5.0035327. [DOI] [PubMed] [Google Scholar]
- 2.Cao J., Lu J. Adaptive synchronization of neural networks with or without time-varying delay. Chaos, Interdiscip. J. Nonlinear Sci. 2006;16(1) doi: 10.1063/1.2178448. [DOI] [PubMed] [Google Scholar]
- 3.Chen M. Synchronization in time-varying networks: a matrix measure approach. Phys. Rev. E. 2007;76 doi: 10.1103/PhysRevE.76.016104. [DOI] [PubMed] [Google Scholar]
- 4.Grigoriev R.O., Cross M.C., Schuster H.G. Pinning control of spatiotemporal chaos. Phys. Rev. Lett. 1997;79:2795–2798. [Google Scholar]
- 5.Pan C., Jiang Y., Zhu Q., Lin W. Emergent dynamics of coordinated cells with time delays in a tissue. Chaos, Interdiscip. J. Nonlinear Sci. 2019;29(3) doi: 10.1063/1.5092644. [DOI] [PubMed] [Google Scholar]
- 6.Ruths J., Ruths D. Control profiles of complex networks. Science. 2014;343(6177):1373–1376. doi: 10.1126/science.1242063. [DOI] [PubMed] [Google Scholar]
- 7.Gao J., Liu Y.Y., D'souza R.M., Barabási A.L. Target control of complex networks. Nat. Commun. 2014;5(1):5415. doi: 10.1038/ncomms6415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Petri G., Expert P., Turkheimer F., Carhart-Harris R., Nutt D., Hellyer P.J., et al. Homological scaffolds of brain functional networks. J. R. Soc. Interface. 2014;11(101) doi: 10.1098/rsif.2014.0873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leng S., Aihara K. Common stochastic inputs induce neuronal transient synchronization with partial reset. Neural Netw. 2020;128:13–21. doi: 10.1016/j.neunet.2020.04.019. [DOI] [PubMed] [Google Scholar]
- 10.Liu D., Zhang P., Zhang Y., Li T., Li Z., Zheng Y., et al. A cost-effective instrument of distributed functional near-infrared spectroscopy for hyperscanning real-world interactions. IEEE Trans. Instrum. Meas. 2023;72:1–10. [Google Scholar]
- 11.Calisto F.M., Santiago C., Nunes N., Nascimento J.C. Breastscreening-ai: evaluating medical intelligent agents for human-ai interactions. Artif. Intell. Med. 2022;127 doi: 10.1016/j.artmed.2022.102285. [DOI] [PubMed] [Google Scholar]
- 12.Mau E.T., Rosenblum M. Optimizing charge-balanced pulse stimulation for desynchronization. Chaos, Interdiscip. J. Nonlinear Sci. 2022;32(1) doi: 10.1063/5.0070036. [DOI] [PubMed] [Google Scholar]
- 13.Dörfler F., Bullo F. Synchronization and transient stability in power networks and nonuniform Kuramoto oscillators. SIAM J. Control Optim. 2012;50(3):1616–1642. [Google Scholar]
- 14.Jalife J. Mutual entrainment and electrical coupling as mechanisms for synchronous firing of rabbit sino-atrial pace-maker cells. J. Physiol. 1984;356(1):221–243. doi: 10.1113/jphysiol.1984.sp015461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Winfree A.T. Springer; 1980. The Geometry of Biological Time, vol. 2. [Google Scholar]
- 16.Strogatz S.H., Abrams D.M., McRobie A., Eckhardt B., Ott E. Crowd synchrony on the millennium bridge. Nature. 2005;438(7064):43–44. doi: 10.1038/43843a. [DOI] [PubMed] [Google Scholar]
- 17.Breakspear M., Heitmann S., Daffertshofer A. Generative models of cortical oscillations: neurobiological implications of the Kuramoto model. Front. Human Neurosci. 2010;4:190. doi: 10.3389/fnhum.2010.00190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tang E., Bassett D.S. Colloquium: control of dynamics in brain networks. Rev. Mod. Phys. 2018;90(3) [Google Scholar]
- 19.Tass P.A. A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biol. Cybern. 2003;89(2):81–88. doi: 10.1007/s00422-003-0425-7. [DOI] [PubMed] [Google Scholar]
- 20.Zuo Z., Cao R., Gan Z., Hou J., Guan C., Leng S. Feedback coupling induced synchronization of neural networks. Neurocomputing. 2023 [Google Scholar]
- 21.Zhou S., Ji P., Zhou Q., Feng J., Kurths J., Lin W. Adaptive elimination of synchronization in coupled oscillator. New J. Phys. 2017;19(8) [Google Scholar]
- 22.Krylov D., Des Combes R.T., Laroche R., Rosenblum M., Dylov D.V. Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence. 2021. Reinforcement learning framework for deep brain stimulation study; pp. 2847–2854. [Google Scholar]
- 23.Naros G., Naros I., Grimm F., Ziemann U., Gharabaghi A. Reinforcement learning of self-regulated sensorimotor β-oscillations improves motor performance. NeuroImage. 2016;134:142–152. doi: 10.1016/j.neuroimage.2016.03.016. [DOI] [PubMed] [Google Scholar]
- 24.Krylov D., Dylov D.V., Rosenblum M. Reinforcement learning for suppression of collective activity in oscillatory ensembles. Chaos, Interdiscip. J. Nonlinear Sci. 2020;30(3) doi: 10.1063/1.5128909. [DOI] [PubMed] [Google Scholar]
- 25.Chen K., Gan Z., Leng S., Guan C. 2022 International Joint Conference on Neural Networks (IJCNN) IEEE; 2022. Deep reinforcement learning with parametric episodic memory; pp. 1–7. [Google Scholar]
- 26.Sari M., Duran S., Kutlu H., Guloglu B., Atik Z. Various optimized machine learning techniques to predict agricultural commodity prices. Neural Comput. Appl. 2024:1–21. [Google Scholar]
- 27.Chen G. Pinning control of complex dynamical networks. IEEE Trans. Consum. Electron. 2022;68(4):336–343. [Google Scholar]
- 28.Yi C., Xu C., Feng J., Wang J., Zhao Y. Pinning synchronization for reaction-diffusion neural networks with delays by mixed impulsive control. Neurocomputing. 2019;339:270–278. [Google Scholar]
- 29.Tang Y., Zhou L., Tang J., Rao Y., Fan H., Zhu J. Hybrid impulsive pinning control for mean square synchronization of uncertain multi-link complex networks with stochastic characteristics and hybrid delays. Mathematics. 2023;11(7):1697. [Google Scholar]
- 30.Qiu X., Yang L., Guan C., Leng S. Closed-loop control of higher-order complex networks: finite-time and pinning strategies. Chaos Solitons Fractals. 2023;173 [Google Scholar]
- 31.Mohseni A., Gharibzadeh S., Bakouie F. The effect of network structure on desynchronization dynamics. Commun. Nonlinear Sci. Numer. Simul. 2018;63:271–279. [Google Scholar]
- 32.Zhu C., Wang X., Zhu L. A novel method of evaluating key nodes in complex networks. Chaos Solitons Fractals. 2017;96:43–50. [Google Scholar]
- 33.Rosenblum M. Controlling collective synchrony in oscillatory ensembles by precisely timed pulses. Chaos, Interdiscip. J. Nonlinear Sci. 2020;30(9) doi: 10.1063/5.0019823. [DOI] [PubMed] [Google Scholar]
- 34.Yuan Z., Zhao C., Di Z., Wang W.X., Lai Y.C. Exact controllability of complex networks. Nat. Commun. 2013;4(1):2447. doi: 10.1038/ncomms3447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang Y., Xiao R. Synchronization of Kuramoto oscillators in small-world networks. Phys. A, Stat. Mech. Appl. 2014;416:33–40. [Google Scholar]
- 36.Schulman J., Wolski F., Dhariwal P., Radford A., Klimov O. Proximal policy optimization algorithms. 2017. arXiv:1707.06347 arXiv preprint.
- 37.Li Q., Zhou T., Lü L., Chen D. Identifying influential spreaders by weighted leaderrank. Phys. A, Stat. Mech. Appl. 2014;404:47–55. [Google Scholar]
- 38.Lü L., Zhang Y.C., Yeung C.H., Zhou T. Leaders in social networks, the delicious case. PLoS ONE. 2011;6(6) doi: 10.1371/journal.pone.0021202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Watts D.J. Strogatz-small world network nature. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 40.Sanz-Arigita E.J., Schoonheim M.M., Damoiseaux J.S., Rombouts S.A., Maris E., Barkhof F., et al. Loss of ‘small-world’ networks in Alzheimer's disease: graph analysis of fmri resting-state functional connectivity. PLoS ONE. 2010;5(11) doi: 10.1371/journal.pone.0013788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lu J., Kurths J., Cao J., Mahdavi N., Huang C. Synchronization control for nonlinear stochastic dynamical networks: pinning impulsive strategy. IEEE Trans. Neural Netw. Learn. Syst. 2011;23(2):285–292. doi: 10.1109/TNNLS.2011.2179312. [DOI] [PubMed] [Google Scholar]
- 42.Yu W., Chen G., Lu J., Kurths J. Synchronization via pinning control on general complex networks. SIAM J. Control Optim. 2013;51(2):1395–1416. [Google Scholar]
- 43.Rothkegel A., Lehnertz K. Irregular macroscopic dynamics due to chimera states in small-world networks of pulse-coupled oscillators. New J. Phys. 2014;16(5) [Google Scholar]
- 44.Barabási A.L. Scale-free networks: a decade and beyond. Science. 2009;325(5939):412–413. doi: 10.1126/science.1173299. [DOI] [PubMed] [Google Scholar]
- 45.Chen J., Dai M., Wen Z., Xi L. A class of scale-free networks with fractal structure based on subshift of finite type. Chaos, Interdiscip. J. Nonlinear Sci. 2014;24(4) doi: 10.1063/1.4902416. [DOI] [PubMed] [Google Scholar]
- 46.Niamsup P., Botmart T., Weera W. Modified function projective synchronization of complex dynamical networks with mixed time-varying and asymmetric coupling delays via new hybrid pinning adaptive control. Adv. Differ. Equ. 2017;2017:1–31. [Google Scholar]
- 47.Orouskhani Y., Jalili M., Yu X. Optimizing dynamical network structure for pinning control. Sci. Rep. 2016;6(1) doi: 10.1038/srep24252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liu H., Xu X., Lu J.A., Chen G., Zeng Z. Optimizing pinning control of complex dynamical networks based on spectral properties of grounded Laplacian matrices. IEEE Trans. Syst. Man Cybern. Syst. 2018;51(2):786–796. [Google Scholar]
- 49.Abrams D.M., Pecora L.M., Motter A.E. Introduction to focus issue: patterns of network synchronization. Chaos, Interdiscip. J. Nonlinear Sci. 2016;26(9) doi: 10.1063/1.4962970. [DOI] [PubMed] [Google Scholar]
- 50.Rajasekar S., Lakshmanan M. Controlling of chaos in Bonhoeffer-van der Pol oscillator. Int. J. Bifurc. Chaos. 1992;2(01):201–204. [Google Scholar]
- 51.Sutton R.S., Barto A.G. MIT Press; 2018. Reinforcement Learning: An Introduction. [Google Scholar]
- 52.Gambuzza L.V., Di Patti F., Gallo L., Lepri S., Romance M., Criado R., et al. Stability of synchronization in simplicial complexes. Nat. Commun. 2021;12(1):1255. doi: 10.1038/s41467-021-21486-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Pikovsky A., Ruffo S. Finite-size effects in a population of interacting oscillators. Phys. Rev. E. 1999;59(2):1633. [Google Scholar]
- 54.Hill A., Raffin A., Ernestus M., Gleave A., Kanervisto A., Traore R., et al. Stable baselines. 2018. https://github.com/hill-a/stable-baselines
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.