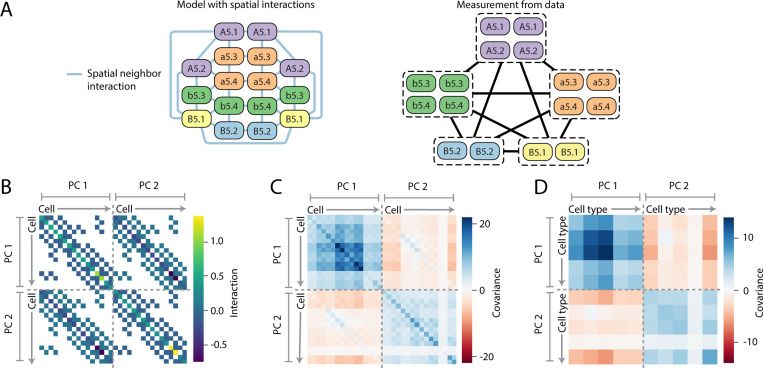
FIG. 5. Structure of statistical physics model with sparse interactions.

(A) Model of the 16-cell stage, where spatial neighbors are directly interacting. In the model we know every cells identity and the covariance between any two cells (left). However, in the data we only know the cell type of each cell and not it’s exact identity (right), hence we can only compute the covariances between cell types. (B) The sparse interaction matrix $J$, for model $p(\mathit{x})=𝓝\left(0,J^{-1}\right)$ where only spatial neighbors have direct interactions, shown for the 16-cell stage with 2 principle components as an example. (C) Dense covariance matrix $J^{-1}$. Note that while $J^{-1}$ is always symmetric, ${\left(J^{-1}\right)}_{(pi)(qj)}\ne {\left(J^{-1}\right)}_{(pj)(qi)}$ in general, even if $J_{(pi)(qj)}=J_{(pj)(qi)}$. (D) Dense matrix of cell type to cell type covariances, corresponding to the model $J$, which, unlike (C), can be directly compared to measurements from data.