FIG. 10.

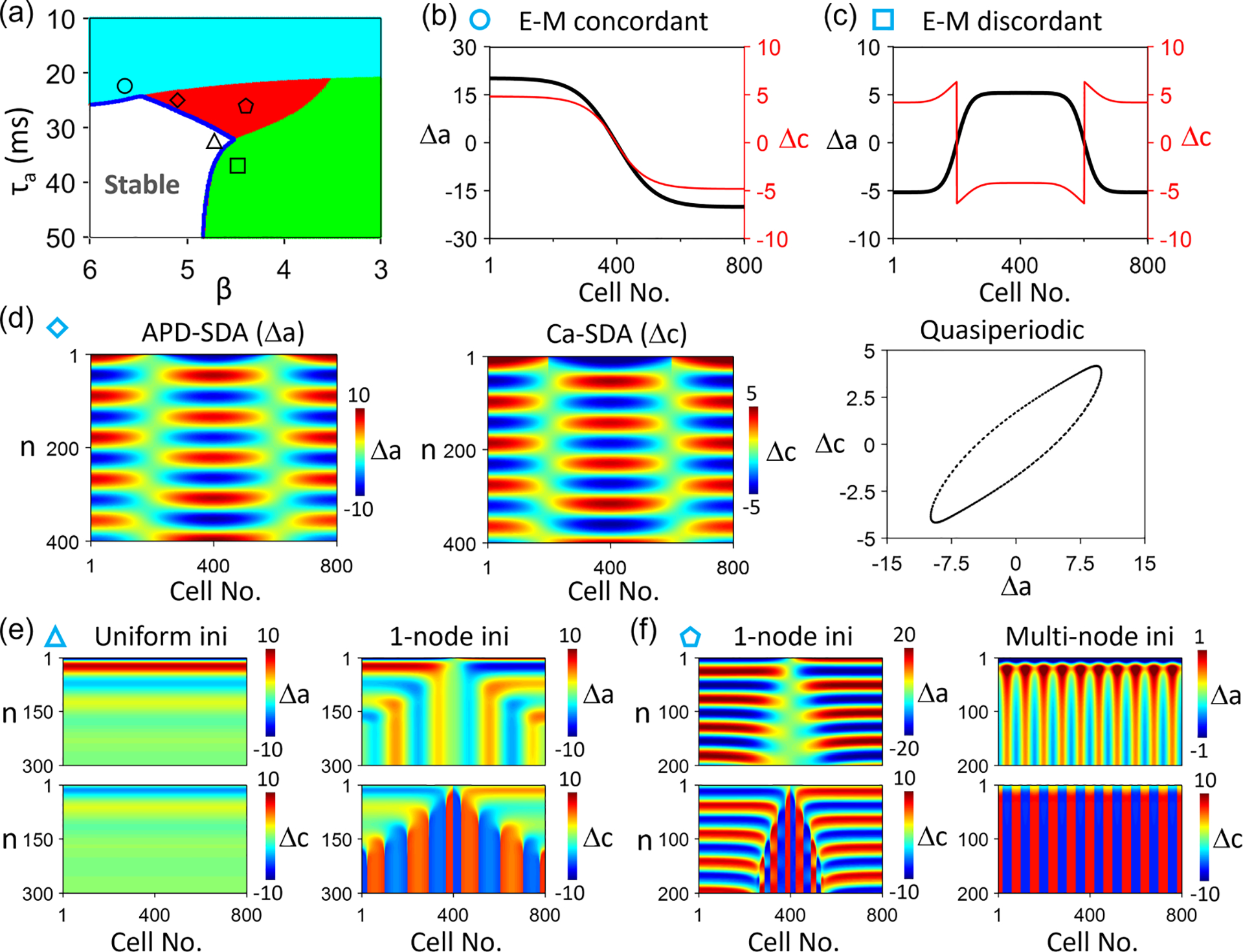
Spatiotemporal Ca and action potential duration (APD) dynamics in the coupled map lattice (CML) model for $\gamma <0$. (a) Phase diagram showing different Ca and APD dynamics vs ${\tau }_a$ and $\beta$ in a single cell. White: stable steady state; cyan: electromechanically concordant alternans; green: electromechanically discordant alternans; and red: quasiperiodicity. $\gamma =-0.002,{\sigma }_R=0.8$, and $=250\text{ms}$. (b) Steady-state $\mathrm{\Delta }a$ (black) and $\mathrm{\Delta }c$ (red) showing an electromechanically concordant spatially discordant alternans (SDA). ${\tau }_a=24$ and $\beta =5.7$, marked by the circle in (a). (c) Steady-state $\mathrm{\Delta }a$ (black) and $\mathrm{\Delta }c$ (red) showing an electromechanically discordant SDA. ${\tau }_a=38$ and $\beta =4.6$, marked by the square in (a). (d) Space-time color-scale plots of $\mathrm{\Delta }a$ (left) and $\mathrm{\Delta }c$ (middle) showing a quasiperiodic SDA (right). ${\tau }_a=24$ and $\beta =5.3$, marked by the diamond in (a). (e) A uniform initial condition leads to a stable steady state (left, no alternans), but a nonuniform (one-node) initial condition leads to multinode electromechanically discordant SDA (right). ${\tau }_a=32$ and $\beta =4.6$, marked by the triangle in (a). (f) A one-node initial condition leads to a quasiperiodic SDA (left), but a multinode initial condition leads to a multinode electromechanically discordant SDA. ${\tau }_a=27$ and $\beta =4.5$, marked by the pentagon in (a). In (e) and (f), the upper panels are color-scale plots of $\mathrm{\Delta }a$, and the lower panels are those of $\mathrm{\Delta }c$.