FIG. 6.

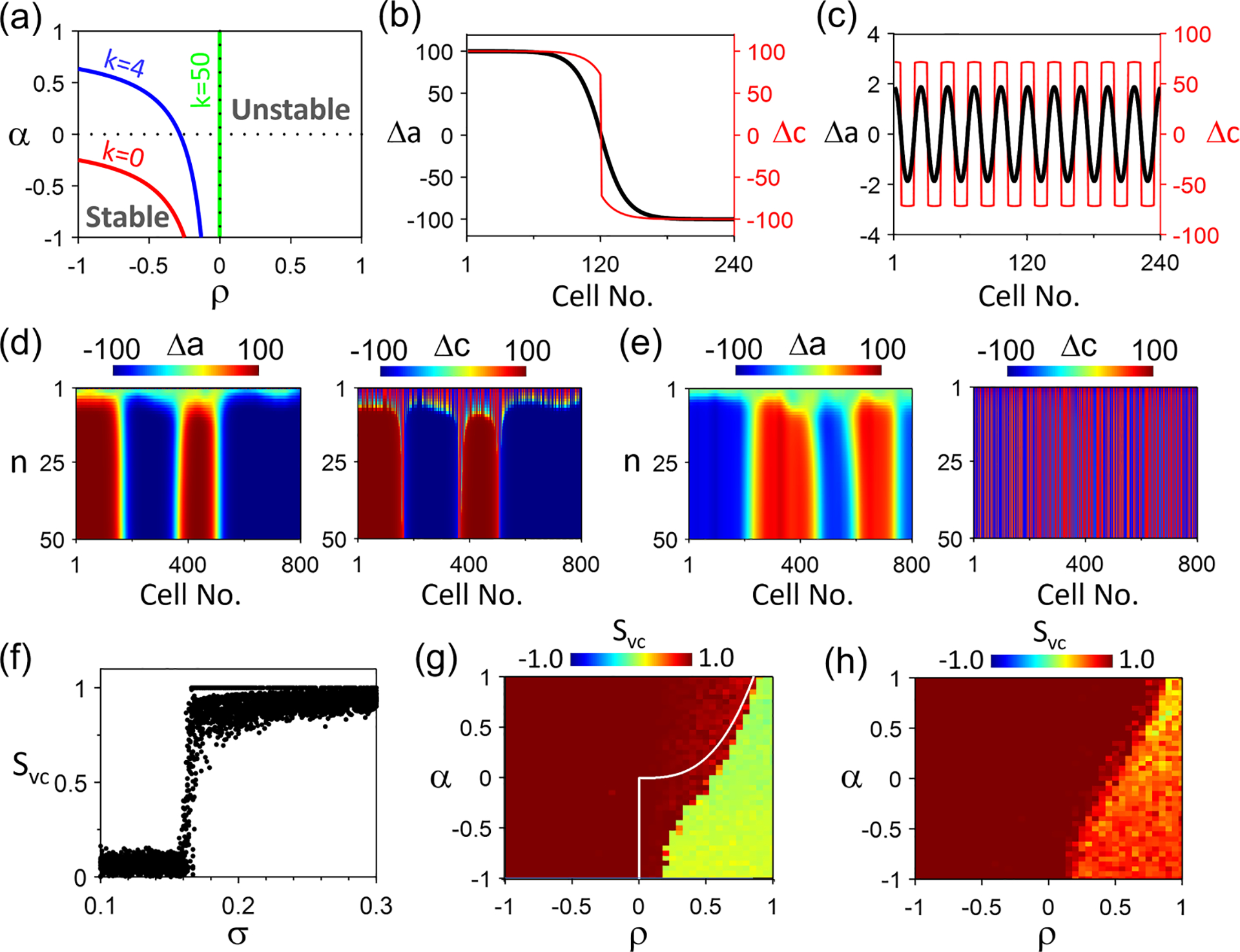
Spatiotemporal Ca and action potential duration (APD) dynamics in the amplitude equation (AE) model for $\gamma \sigma >0$. (a) Stability boundaries (colored lines) in the $\rho -\alpha$ plane for different spatial modes of the linear stability analysis of the steady state. Shown are the boundary for $k=0$ (red), 4 (blue), and 50 (green). $\gamma =0.5$ and $\sigma =0.5$. (b) Steady-state $\mathrm{\Delta }a$ (black) and $\mathrm{\Delta }c$ (red) in space for beat no. 100 with 1 node in both $\mathrm{\Delta }a$ and $\mathrm{\Delta }c$. (c) Same as (b) but with 20 nodes in both $\mathrm{\Delta }a$ and $\mathrm{\Delta }c$. (d) Space-time plots of $\mathrm{\Delta }a$ and $\mathrm{\Delta }c$ with an initial condition of $\mathrm{\Delta }a=0$ and random $\mathrm{\Delta }c$ in which $\mathrm{\Delta }c$ is a binary number, uniformly chosen as either −100 or 100. $\gamma =0.5$ and $\sigma =0.5$. (e) Same as (d) but with $\sigma =0.1$. (f) $S_{vc}$ vs $\sigma$. For each $\sigma ,20S_{vc}$ values from different initial conditions as in (c) and (d) are plotted. $\gamma =0.5$. (g) Color map of $S_{vc}$ vs $\alpha$ and $\rho$. For each set of $\alpha$ and $\rho$, one random initial condition (spatial scale $l=1$ cell) is simulated. $\gamma =0.5$ and $\sigma =0.3$. The white line is the synchronization boundary predicted by Eq. (13) under $\gamma =0$, showing that positive Ca-to-APD coupling ($\gamma >0$) enhances spontaneous synchronization. (h) Same as (g) but with a larger spatial scale of the initial conditions: $l=20$ cells.