Energy store & release facilitating movement in stick & slip friction, animal jump, and earthquake

Abstract

Nature abounds in examples of evolutionary designs (bio and non-bio) that evolve freely into configurations that provide easier and greater access for movement. The present article considers three seemingly unrelated phenomena that appear to obstruct flow: stick–slip friction, animal jump, and earthquake. The analysis is based on simple models of rhythmic energy store & release motion. In each case, the rhythm is the sole degree of freedom. The analyses show that stick–slip friction facilitates movement because the coefficient of static friction is greater than the coefficient of sliding friction. Next, all forms of animal locomotion under gravity consist of cycles of energy storage (jump to a height) and energy release (forward fall). The rhythm of the cycle is natural such that the forward advance of the animal is economical. Finally, the onset of the earthquake is modeled the same way, as shear stresses at the rock-on-rock interface, which are matched by bending stresses in the bent ‘blades’ of rock contained between fissures perpendicular to the interface. In sum, naturally evolved store & release rhythm facilitates the movement, contrary to the commonly held impression.

Introduction

Nature just issued a call to engineers to publish their ideas in Nature journals¹. This article responds to that call with a holistic engineering view of diverse phenomena that cover all realms (bio and non-bio) but have not been recognized as related, and then questioned.

Evolution throughout nature offers abundant evidence that flow systems that have freedom to morph evolve into configurations (designs) that provide greater access to what moves and flows. Examples cover all realms and scales: animal locomotion (from houseflies to jumbo jets)², river basins and deltas^3,4, pedestrian movement⁵, lung architecture and function⁶, city evolution⁷, air traffic, economy, technology evolution, and many more evolutionary designs reviewed in Refs.^8,9. The time direction of these evolutionary designs confirms the time arrow of evolution in nature¹⁰.

Recently I questioned the unanimity of such conclusions¹¹. As test to falsify¹² the universality of the evolution of flow configuration toward progressively greater access, I chose three common phenomena that seem to obstruct flow: cataracts¹³, hydraulic jumps¹⁴, and roll waves of rainwater on the pavement¹⁵. Contrary to their appearance, these evolutionary designs facilitate flow access. This unexpected conclusion aligns itself with earlier examples of flow designs have been shown to facilitate access (transport) instead of the impression that they obstruct access: turbulence scraping a wall¹⁶, respiration and other rhythmic physiological processes and technologies inspired by such processes (periodic ice making, surface cleaning, power plant downtime for repair and renewal)⁸.

In this article I submit to the same test another widespread phenomenon that gives the impression of obstructing movement: the alternating sticking and sliding of the interface between two bodies with relative motion. The test is predictive (theory), not descriptive (experiment). Does the stick–slip phenomenon obstruct or enhance relative motion?

Sticking and sliding phenomena are observed over a broad range of scales^17–22, from a metal piece being turned in a lathe, to active seismic zones where an earthquake (movement and sound) is triggered by the sudden change from sticking to sliding. The most common screeching sounds betray the presence of the stick-slide phenomenon: car tires and train wheels coming to an abrupt stop, basketball shoes on the parquet, squeaky-clean skin, and the sound of the bow on the chords of the violin and similar string instruments. While questioning what seems to be obvious, we will discover that the performance of rhythmic phenomenon is relevant to a host of previously unrelated examples from animal locomotion^23–29 and machines and athletics with throwing motion³⁰.

Stick–slip friction

Consider the cycle of stick & slide motion modeled in Fig. 1. The motion is on a horizontal plane. The coefficient of static friction (μ₁) is comparable with (but greater than) the coefficient of kinetic (sliding) friction (μ₂)^31,32. The weight Mg is pulled to the right by a force applied to the right end of a linear spring. The spring constant is k, meaning that the tensile force in the spring is kL, where L is the elongation of the spring (i.e. L = 0 when the spring is relaxed).

Figure 1.

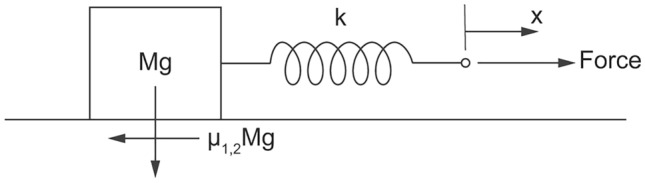
Spring-mass model of body with energy store & release motion.

In the beginning, the spring is relaxed and the weight is stuck on the plane. The applied force stretches the spring to the distance L during the time t₀, until the tensile force in the spring matches the force needed to dislodge the weight and start its movement:

$$\text{k L}={\mu }_1\text{Mg}.$$ 1

As the weight slides to the right, the energy stored in the spring is converted into the kinetic energy of the body,

$$\frac{1}{2}k{L}^2=\frac{1}{2}M{V}^2.$$ 2

V is the velocity at the end of acceleration, i.e. when the spring is relaxed. The friction force is μ₂Mg, the body slides to the distance x and dissipates its kinetic energy by friction (μ₂),

$$\frac{1}{2}M{V}^2={\mu }_{2}Mgx.$$ 3

The time of travel to the step x is

$$t_x=\frac{x}{V}.$$ 4

Equation (4) is an order of magnitude statement. A more exact analysis would have to account for the fact that (during energy release) the speed V increases from zero to a maximum when the spring is relaxed. From Eqs. (1)–(4) we learn that $\text{L}={\mu }_1\text{Mg}/k$, $\text{V}=L{(k/M)}^{1/2},$ and $\text{x}=k{L}^2/(2{\mu }_{2}Mg)$. The sliding time interval becomes:

$$t_x=\frac{1}{2}\frac{{\mu }_1}{{\mu }_2}{\left(\frac{M}{k}\right)}^{1/2}.$$ 5

After the time step t_x, the spring is relaxed, and the weight remains stationary. To complete the cycle and restart the motion, the right end of the spring must be moved with the speed scale V to a new distance L during the stretching time t₀,

$$t_0=\frac{L}{V}={\left(\frac{M}{k}\right)}^{1/2}.$$ 6

The work dissipated during one cycle is expressed in Eqs. (2) and (3). The duration of one cycle is t_x + t₀. The power dissipated during one cycle is

$$P=\frac{{\mu }_{2}Mgx}{t_x+t_0}={\mu }_{2}MgV\frac{1}{1+2{\mu }_2/{\mu }_1},$$ 7

where V represents the speed of the mass-spring assembly (with the spring extended to L) as it moves to the right. The dissipated power P does not depend on the spring constant k because the spring is a conservative (reversibly changing) system, not a dissipative (irreversibly changing) system.

We recognize two extremes of Eq. (7). If the static friction coefficient is larger than the kinetic friction coefficient, ${\mu }_1>{\mu }_2,$ the power spent is

$$P\cong {\mu }_{2}MgV.$$ 8

Note that in this limit the power dissipation (8) is the same as when the sticking phenomenon is absent. In the second extreme μ₁ is equal to μ₂, and the power spent is

$$P=\frac{{\mu }_2}{3}MgV.$$ 9

The phenomenon of stick & slip resides between the limits (8) and (9). In conclusion, the stick & slip phenomenon enhances the access of the body as it slides on the plane surface. This conclusion comes from the fact that although comparable, ${\mu }_1$ is greater than ${\mu }_2$. Eqs. (8) and (9) represent the two extremes of Eq. (7). The extremes determine the range of possibilities, namely Eqs. (8) and (9), which is 1/3 of Eq. (8). Note that Eq. (7) shows the effect of the ratio ${\mu }_2/{\mu }_1$, which is in accord with the factor ${(1+2{\mu }_2/{\mu }_1)}^{-1}$.

Animal locomotion

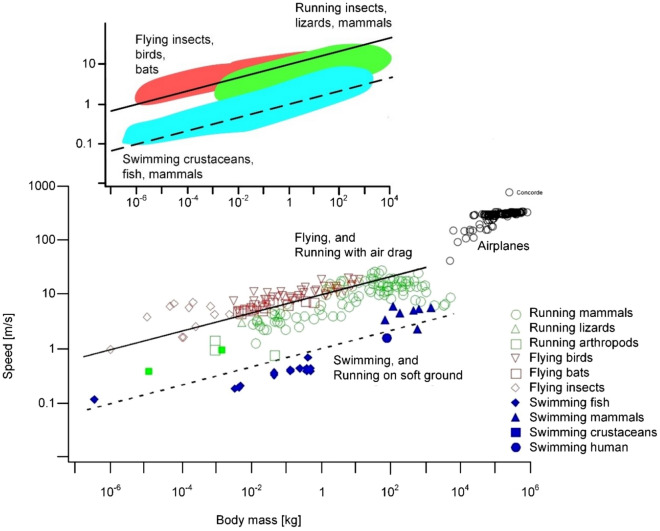
Animals of all sizes in all media (water, land, air) exhibit a periodic movement (Fig. 2) with features predicted based on a model with one degree of freedom, the cruising speed of forward advance—or, alternatively, the frequency of body undulation (leg stride, wing flapping, fishtailing)^2,8. The predicted results agree with animal measurements. The agreement is manifested in several equivalent ways: the horizontal speed is proportional to the body mass M raised to the power 1/6 (cf., Fig. 3); the speed is proportional to the body length scale raised to the power 1/2; or the height (jump) and the distance traveled during one cycle (body lift & fall forward) are proportional to the body length scale.

Figure 2.

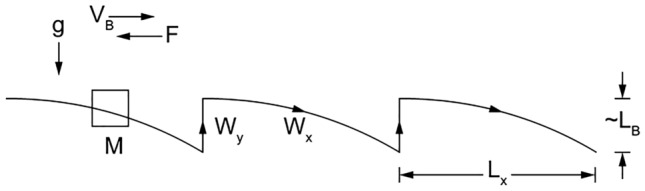
The two-step cycle of animal locomotion theory.

Figure 3.

The universal scaling of steady locomotion in all media on earth (after Ref.²). The labels on the axes in the upper graph are the same as on the axes in the lower graph.

As shown in Fig. 3, the agreement with theory is accompanied by the diversity compacted in the clouds of data. The diversity is predictable as well if one accounts for additional features (degrees of freedom) in the assumed model of the moving body. Examples of additional features are the slenderness of the body and the lifestyle of the animal (predator vs. prey³³).

Cases that deviate significantly from the predicted alignment are recognized in the literature as ‘outliers’: these are waiting to be reunited in the physics of evolution of animal design. Examples of extreme outliers are animal bodies driven by stored elastic energy, which is released suddenly by latch-like mechanisms. Best known outliers are fleas and grasshoppers, which jump to heights and distances orders of magnitude greater than their body length scale. Aquatic animals with store & release locomotion (such as spiny lobsters¹⁷) are recognized in zoology.

The hint that the energy store-release design is predictable comes from the observation that aquatic animals that propel themselves with store-release energy travel during one step to a considerably shorter distance than the insects: in water the jump is comparable with the body length scale. Clearly, the medium in which the store-release design propels the body is an important participant.

This suggests a modification of the spring-mass model of Fig. 1, in which the medium is the horizontal plane, and the slowdown is caused by friction. In store-release locomotion, the medium is the surrounding fluid. Equation (2) continues to hold: $\frac{1}{2}k{L}_b^2$ is the energy stored in the elastic organ, L_b is the body length scale, and $\frac{1}{2}M{V}^2$ is the kinetic energy of the body immediately after the release of the stored energy. The kinetic energy is dissipated by overcoming fluid friction (drag force F_D) during travel to the distance x. Employing the rules of scale analysis¹⁶, in which “ ~ ” means ‘equal in an order of magnitude sense’, the first law of thermodynamics requires,

$$\frac{1}{2}M{V}^2\sim F_{D}x.$$ 10

The drag force is calculated with the following formula, which serves as definition for the drag coefficient C_D available for experiments and graphically¹⁶,

$$F_D\sim C_D{L}_b^2\frac{1}{2}{\rho }_a{V}^2,$$ 11

where ρ_a is the density of the ambient fluid (air, water). If the Reynolds number based on L_b and V (namely Re = VL_b/ν_a) is of order 10–100 or greater, C_D is essentially constant and of order 1. If Re is smaller than this range, then C_D is proportional to ${\text{Re}}^{-1}$. Equation (11) is not derived from existing theories. Note that Eq. (11) is an empirical correlation of measurements of the drag force (F_D) experienced by objects suspended in a uniform flow field (V). The form of the correlation serves as definition of the drag coefficient C_D¹⁶.

Continuing with the assumption that Re is greater than 10–100, and in view of the body mass scaling

$$M\sim {\rho }_b{L}_b^3.$$ 12

we find that Eqs. (10)–(12) yield,

$$x\sim L_b\frac{{\rho }_b}{{\rho }_a},$$ 13

where ρ_b is the body density. Results from the same analysis are,

$$V\sim L_b{\left(\frac{k}{M}\right)}^{1/2},$$ 14

$$t_x\sim \frac{{\rho }_b}{{\rho }_a}{\left(\frac{M}{k}\right)}^{1/2},$$ 15

where t_x is the time step of the jump to the distance x, namely t_x ~ x/V.

The main conclusion comes from Eq. (13). The jump (x) is greater than the body length scale (L_b) by a factor of order ${\rho }_b/{\rho }_a$. In air the ratio ${\rho }_b/{\rho }_a$ is of order 10²–10³ and accounts for the extraordinary jumping ability of some insects. In water, the ratio ${\rho }_b/{\rho }_a$ is of order 1, and is the reason why the aquatic store-release movement consists of shorter steps comparable with the body length scale.

Next, for smaller bodies with Re values below 10–100, C_D is replaced by Re^–116 and Eq. (13) becomes,

$$x\sim L_b\frac{{\rho }_b}{{\rho }_a}\text{Re},$$ 16

where

$$\text{Re}\sim \frac{V{L}_b}{{\nu }_a}\sim \frac{1}{{\nu }_a}{\left(\frac{k{L}_b}{{\rho }_b}\right)}^{1/2}.$$ 17

and ν_a is the kinematic viscosity of the medium. Equation (16) shows that in the case of smaller bodies the jumping distance x falls below the estimate determined for the large-Re range. In other words, for the flea the x/L_b ratio should be expectedly smaller than for the grasshopper.

To shed light on the question on whether the store-release design is an economic way to move, let us compare it with the rhythmic design that unites most animals^2,9. To place the comparison of animals on the same basis assume that C_D is a constant of order 1, which means that the body is big enough such that Re > 10–100. The work done rhythmically per unit travel is of order^2,8

$$W^{\prime }\sim {\left(\frac{{\rho }_a}{{\rho }_b}\right)}^{1/3}Mg.$$ 18

The dimensions of W’ are [J/m] because the dimensions of M[kg]g[ms^–2] are N (= J/m). Equation (18) shows that the $W^{\prime }[J/m]$ value of a flying animal (size M) is roughly one tenth of the $W^{\prime }$ value of a swimmer of the same size [because ${({\rho }_a/{\rho }_b)}^{1/3}\sim \frac{1}{10}$ in air, and ${({\rho }_a/{\rho }_b)}^{1/3}$ ~ 1 in water].

The stick-slide work done per unit travel is of order,

$$W_{s-s}^{\prime }\sim \frac{1}{2}k{L}_b^2\frac{1}{x}.$$ 19

To have both kinds of locomotion, $W^{\prime }$ and $W_{s-s}^{\prime }$, the body must be strong. Here, the word ‘strong’ has the meaning of powerful, or forceful (not weak), as the description of a weightlifter and a wrestler at the Olympics. In the case of Eq. (18), the body strength is represented by the body weight Mg lifted to a height of order L_b during each cycle of lifting and falling forward. Lifting a weight is equivalent to stretching vertically a constant-force spring (Fig. 4). The force in such a spring is Mg, and the displacement of the top end of the spring (where M is located) relative to the fixed end of the spring (the ground) is the height (L_b) to which M is lifted.

Figure 4.

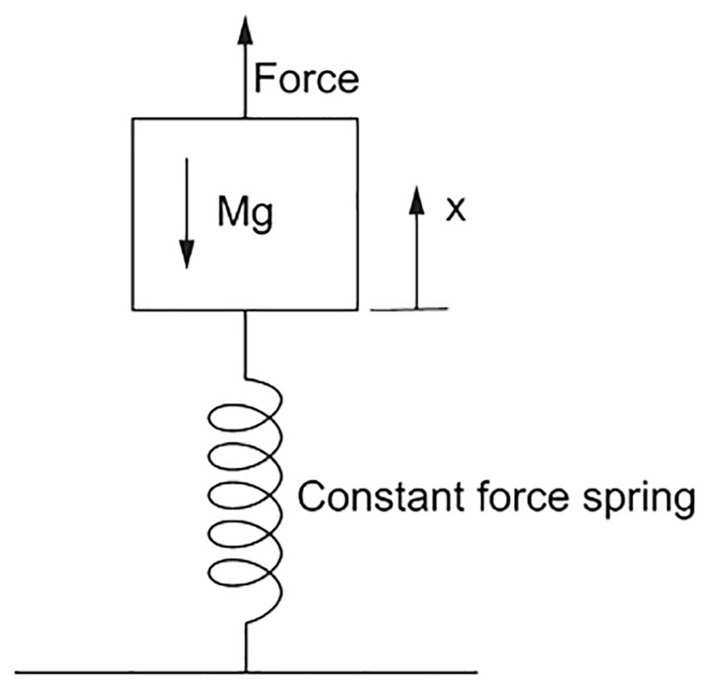
Model of lifting a weight, viewed as stretching a constant-force spring.

Stretching the spring that drives the store-release movement requires a force of size kL_b. To compare the two movements on the same basis, assume that the two movers are equally strong:

$$Mg\sim k{L}_b.$$ 20

With this assumption, Eqs. (18)–(20) yield the ratio of the competing efforts:

$$\frac{W_{s-s}^{\prime }}{W^{\prime }}\sim \left(\frac{{\rho }_a}{\rho _b^{}}\right)_{}^{2/3}.$$ 21

In air this ratio is of order ${10}^{-2},$ and indicates a dramatic advantage in favor of store-release movement. In water, the per-unit efforts are of the same order of magnitude $W_{s-s}^{\prime }/W^{\prime }\sim 1$.

The store & release motion is not the only way that animals move on earth. Certain insects and aquatic animals are unique (outliers) because of their lifestyle, predator, or fear of becoming prey. It is the same with the ‘uniqueness’ of the long neck of the giraffe, which evolved to provide the animal with access to high leaves and fruit. Seemingly different than the animals considered in Sect. "Animal locomotion" are the crawlers, snakes, and reptiles on land, with their predecessors (the fish) in water. They do not coil and recoil, but they all have locomotion because of the energy store & release cycle imagined in Fig. 2. They all must lift weight (including the fish²) before being able to advance by overcoming drag. The fish is not fighting gravity only when it is asleep. When swimming, the fish must get the water out of the way, and the only direction for that water packet to go is upward because the upper surface is free (deformable) and the bottom is rigid.

Earthquake

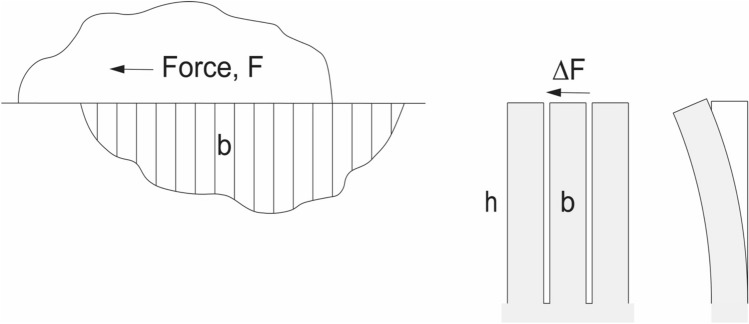
Another example of energy store & release is the motion of two rock layers with pressure at the interface. This periodic motion has been studied descriptively, based on several models reviewed in Refs.^34–36. The classical models account for a ‘noisy’ and random phenomenon, not for a periodic stick–slip phenomenon. The models conform to the reality that the earthquake onset is impossible to anticipate because of local randomness in the features of fissured bodies^37,38. This is not questioned. However, part of the same reality is that before the earthquake onset, the mating bodies are stressed by shear forces (e.g. F in Fig. 5), and that the solid ‘slabs’ between fissures bend under the shear forces at the body-body interface. This is the view that connects the present model of an earthquake with the diverse store & release phenomena theorized in Sects. "Stick–slip friction" and "Animal locomotion".

Figure 5.

Model of energy store & release motion when two bodies of rock are pressed against each other, and one body develops vertical cracks because of shear at the horizontal interface.

The assumption h/b > 10 refers to the present model and to the ‘comb’ example discussed later. This assumption is made for simplicity. It means that the deformation of the solid ‘blades’ is due primarily to bending stresses [tensile stresses in the dorsal portions of blades, and compressive stresses in the ventral portions]. Generally, the deformation of a solid blade is due to a combination of bending stresses and shear stresses³².

In Fig. 5 the upper layer is pushed to the left while being stuck to the lower layer. The lower layer develops cracks because of shear at the interface. The shear force F is proportional to μ₁, namely F = μ₁Mg where Mg is the weight of the upper layer. The cracks are modeled as perpendicular to the interface. Between the cracks emerges a stack of vertical rock layers that undergo bending. Their tips bend in the direction of the shear force at the interface.

Assume that each vertical layer is slender, with h/b > 10 as shown in Fig. 5. The cracks allow the vertical layers to bend slightly with negligible friction between them. Each vertical layer is approximated by a two-dimensional elastic blade of height h and thickness b. The blade is in pure bending. The deflection of the tip is,

$$\delta =\frac{\mathrm{\Delta }F{h}^3}{3EI}.$$ 22

where ΔF is the fraction of the shear force supported by the top of one blade, E is the rock modulus of elasticity, and I is the area moment of inertia of the blade cross section:

$$I=\frac{b{h}^3}{12}.$$ 23

In pure bending, the cross sections of the vertical blade remain plane while they rotate slightly as the blade becomes curved. The tips turn and the rock layer develops ridges at the interface with the upper layer. Although the upper and lower rock layers are still stuck, the deformed blades are a spring that is extended to the left to the distance δ under the horizontal force ΔF. The spring constant is

$$k=\frac{\mathrm{\Delta }F}{\delta }=\frac{1}{4}Eb.$$ 24

Beyond this point in the model, the analysis and conclusions of Sect. "Stick–slip friction" apply. The upper and lower layers remain stuck until the force experienced by the spring (the tops of the blades) matches the tangential force of static friction due to the interfacial pressure.

The spring constant [k, Eq. (24)] plays an important role in stick–slip motion during an earthquake. Sparse cracks (large b) and stiff rock contribute to the effect of a stiff spring, i.e. to a large shear force and the delay of sliding motion. When cracks multiply (small b) the shear force needed for sliding is smaller, and sliding starts sooner.

One can play with a tooth comb to develop a feel for the physics captured by the model of Fig. 5. Press your palm against the teeth and pull the comb across the teeth. Each tooth bends independently of its neighbors. Pull harder, and suddenly your palm slides along those tips. If you do not like the tickling feeling, replace your palm with a piece of rubber such as an eraser.

Conclusion

The conclusion from this article is that energy store & release motion deserves renewed scrutiny. The main result of this investigation is that three seemingly unrelated classes of phenomena can be modeled as periodic movement in one direction, driven by energy storage and release. The previously not connected phenomena are stick–slip friction, animal locomotion, and rock-on-rock slip during earthquake onset. Essentially, one simple mental viewing (one idea) connects all three classes and leads to the conclusion that energy store & release motion facilitates movement. This conclusion is theoretical and, like any theory that connects disparate phenomena, it deserves to be tested against data and notions available separately in mature fields.

Indeed, this was the declared purpose of this work. Its original title in the manuscript was posed as a question, “Is energy store & release obstructing or facilitating movement?” Before revisions, the journal informed me that the title must not be a question, therefore I changed it to “Energy store & release facilitating movement in stick–slip friction, animal jump, and earthquake”.

The first reviewer asked whether there exist other phenomena that can be investigated and explained according to this theory. I am sure there are. In this article I brought together three unlikely relatives. The way to identify more relatives is to recognize and then question the rhythmic movements that abound in nature. What drives each rhythmic movement is a secondary question. One must question the rhythm because science education is dominated by lessons about steady flow and static models.

A tendency toward greater (easier) access governs the evolution of rhythmic configurations that give the impression that they decrease access to movement. Beginning with Sect. "Stick–slip friction", the analyses showed that energy store & release rhythms are natural, predictable, and they facilitate movement.

The second reviewer felt that the use of ‘greater access’ sounds vague. The expression of “greater access’ comes from the constructal law, which is the physics principle that governs the occurrence and evolution of all flow designs, animate and inanimate^2,8,39. The word ‘access’ was used intentionally, to be all-inclusive, and to avoid field-specific expressions in use, such as minimum flow resistance in hydrology and blood vasculature⁴⁰, minimum travel time in urban design, minimum work in locomotion, maximum efficiency in machines, and ‘least action’ in the 1700s mechanics. Superlatives such as optimum, maximum, minimum, most, and least, do not appear in the constructal law because “end design” is not part of nature. Evolution has no end. All phenomena of evolution are about directionality: change after change in a discernible direction in time.

Furthermore, the constructal law has not been refuted since its multiple disclosures in 1996–1997^41–44. It was not refuted even in cases chosen to refute it¹¹. During the first decade of its spreading, the constructal law appeared primarily in engineering and applied physics publications. Then, after the publication of constructal law books for the general audience^8,45–48, we are seeing a surge in publications bearing related labels of design phenomenon (constructor, live matter, assembly, canalization, anomalous diffusion, pattern in nature, topology optimization⁴⁹, etc.).

The second reviewer also felt that “naturally evolved” seems ambiguous. He questioned whether by ‘natural evolution’ I mean ‘spontaneous emergence phenomena that are not tuned but just find an optimum by themselves.’ I considered such questions in the 1980s, before the constructal law was formulated. Evolution means everything, all phenomena of change in configuration (flow, movement, internal and external) in a discernible direction in time. Spontaneous, young, and mature are all evolutionary designs in nature. In the study of evolution, the physical phenomenon that had been overlooked was the design (the form, the configuration) and its occurrence and change with direction in time.

Freedom was the overlooked physical property present in all evolving systems. Freedom is universally and naturally present, because without freedom no change is possible. In sum, all evolving designs are natural, including the ‘human and machine’ species⁵⁰.

The reviewer also recommended clarification of the adjective ‘predictive’, which applies to the ideas communicated in the present article. There are two kinds of scientific inquiry, predictive (called ‘theory’) and descriptive (called ‘empiricism’). Theory and empiricism are opposites in how the mind proceeds in time:

Theory is a purely mental viewing, called ‘idea’, a word from the ancient Greek verb idein (to see with the eyes of the mind). The idea happens before the thinker looks at nature, to test the validity of the idea. With a theory we predict.

Empiricism proceeds in the opposite direction in time. First, the thinker observes, measures and records one or more features of an object in nature (e.g. the speed of a bird, the image of a snowflake, etc.). Afterwards, the thinker describes the observations. This is empiricism, the facts, the data, the reality. In cases where the narrator is more curious and gifted, the description is followed by explanation, which is the attempt to account for the observed features by referencing existing principles and older observations.

None of the acts mentioned in the preceding paragraphs are present in this article, which is why this article is theory, not empiricism. It takes new language to put together the stick–slip friction with the earthquake and the animal jump. Theoretical acts of climbing over the fence and stepping off the curb are possible, which is why metaphors are useful in scientific work⁵¹.

List of symbols

b

Blade thickness, m

C_D

Drag coefficient

E

Modulus of elasticity, Nm^–2

F

Force, N

F_D

Drag force, N

g

Gravitational acceleration, m s^–2

h

Blade height, m

I

Area moment of inertia, m⁴

k

Spring constant, N m^–1

L

Length, m

L_b

Body length scale, m

M

Mass, kg

P

Power, W

Re

Reynolds number

t₀

Stretching time, s

t_x

Sliding time, s

V

Speed, m s^–1

W’

Work dissipated per unit travel, J m^–1

x

Displacement, m

Greek symbols

δ

Deflection, m

μ₁

Static friction coefficient

μ₂

Kinematic friction coefficient

ν_a

Kinematic viscosity, m²s^–1

δ_a

Ambient density, kg m^–3

δ_b

Body density, kg m^–3

Author contributions

A.B. wrote the manuscript and designed the figures.

Data availability

All data generated or analysed during this study are included in this published article.

Competing interests

The author declares no competing interests.