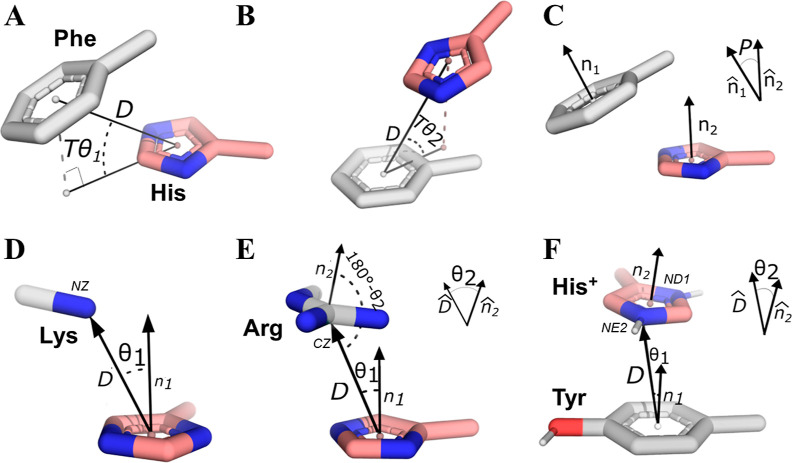
Figure 1.

Selected geometrical parameters to represent aromatic–aromatic and cationic–aromatic interaction conformations involving histidine. (A–C) Definition of parameters for a His–Phe pair, where D is the distance between the centroids of the His ring (pink with the nitrogen atoms colored in blue) and the Phe ring (gray), Tθ₁ is the elevation of the Phe centroid relative to His, Tθ₂ is the elevation of His relative to the Phe centroid, and P denotes the angle between the normal vectors of the aromatic rings of the paired His and Phe residues, provided P ≤ 90°. (D–F) Definition of parameters for amino acid pairs involving His and Lys, Arg, or Tyr based on ref (24). (D) Parameters for a His⁰–Lys pair, where θ₁ describes the angle between the NZ atom of Lys and the normal of the His ring’s plane (represented by the n1 vector), where D is the distance of the NZ atom from the ring centroid. (E) For the His⁰–Arg pair, an additional parameter, θ₂, denotes the angle of the normal to the Arg’s plane and the direction of the vector D. (F) Parameters for a His⁺–Tyr pair, where the distances and angles are taken from the closest His nitrogen (NE2 or ND1) for a given pair. The geometric parameters (panels A–C) are illustrated for His–Phe, with the same parameters used for the other pairwise interactions (as His–Trp). All the pairwise interactions between two rings (i.e., aromatic–aromatic pairs and cationic–aromatic pairs in which His serves as the cation) were characterized using the three parameters D, P, and Tθ₂, being the elevation of His from its partner’s ring. We note that, in the definition of Tθ₁ in the context of homogeneous His–His pairs, this angle refers only to the order of their assignment (with His chosen first as the reference). In these cases, both elevation angles were calculated for the two scenarios. All cationic–aromatic systems (panels D–F) were characterized using D and θ₁. For His⁺ and Arg as cations, also θ₂ was considered.