Skip to main content
PMC home page
Heliyon logoLink to Heliyon
. 2024 Jul 31;10(15):e35451. doi: 10.1016/j.heliyon.2024.e35451

Proximal humeral bone density assessment and prediction analysis using machine learning techniques: An innovative approach in medical research☆

Gen Li a,1, Nienju Wu a,1, Jiong Zhang a,1, Yanyan Song b, Tingjun Ye a, Yin Zhang a, Dahang Zhao a, Pei Yu a,⁎⁎, Lei Wang a,⁎⁎⁎, Chengyu Zhuang a,⁎
PMCID: PMC11334883  PMID: 39166094

Abstract

Background

Patients with fractures of the proximal humerus often local complications and failures attributed to osteoporosis. Currently, there is a lack of straight forward screening methods for assessing the extent of local osteoporosis in the proximal humerus. This study utilizes machine learning techniques to establish a diagnostic approach for evaluating local osteoporosis by analyzing the patient's demographic data, bone density, and X-ray ratio of the proximal humerus.

Methods

A cohort comprising a total of 102 hospitalized patients admitted during the period spanning from 2021 to 2023 underwent random selection procedures. Resulting in exclusion of 5 patients while enrolling 97 patients for analysis encompassing patient demographics, shoulder joint anteroposterior radiographs, and bone density information. Using the modified Tingart index methodology involving multiple measurements denoted as M1 through M4 obtained from humeral shafts. Within this cohort comprised 76 females (78.4 %) and 21 males (21.6 %), with an average age of 73.0 years (range: 43–98 years). There were 25 cases with normal bone density, 35 with osteopenia, and 37 with osteoporosis. Machine learning techniques were used to randomly divide the 97 cases into training (n = 59) and validation (n = 38) sets with a ratio of 6:4 using stratified random sampling. A decision tree model was built in the training set, and significant diagnostic indicators were selected, with the performance of the decision tree evaluated using the validation set. Multinomial logistic regression methods were used to verify the strength of the relationship between the selected indicators and osteoporosis.

Results

The decision tree identified significant diagnostic indicators as the humeral shaft medullary cavity ratio M2/M4, age, and gender. M2/M4 ≥ 1.13 can be used as an important screening criterion; M2/M4 < 1.13 was predicted as local osteoporosis; M2/M4 ≥ 1.13 and age ≥83 years were also predicted as osteoporosis. M2/M4 ≥ 1.13 and age <64 years or males aged between 64 and 83 years were predicted as the normal population; M2/M4 ≥ 1.13 and females aged between 64 and 83 years were predicted as having osteopenia. The decision tree's accuracy in the training set was 0.7627 (95 % CI (0.6341, 0.8638)), and its accuracy in the test set was 0.7895 (95 % CI (0.6268, 0.9045)). Multinomial logistic regression results showed that humeral shaft medullary cavity ratios M2/M4, age, and gender in X-ray images were significantly associated with the occurrence of osteoporosis.

Conclusion

Utilizing X-ray data of the proximal humerus in conjunction with demographic information such as gender and age enable the prediction of localized osteoporosis, facilitating physicians' rapid comprehension of osteoporosis in patients and optimization of clinical treatment plans.

Level of evidence

Level IV retrospective case study.

Keywords: Proximal humerus fracture, Osteoporosis, Tingart index, Machine learning, Decision tree research

1. Introduction

The proximal humerus is a common location for osteoporosis-related fractures, accounting for 6 % of all fractures and ranking third among osteoporosis-related fractures [1]. There are several treatment options available for fractures, tailored to the specific type. Among these, open reduction and internal fixation using a plate is the most prevalent surgical approach [2]. However, local bone loss at the proximal humerus often leads to complications such as plate malposition, screw protrusion, and implant loosening (with an incidence rate of 12.8–22.5 %) postoperatively, sometimes requiring revision surgery [[3], [4], [5]]. Therefore, accurately assessing the local bone volume in the proximal humerus before surgical intervention is essential.

Currently, the gold standard for diagnosing osteoporosis is bone mineral density testing based on DXA values, which primarily incorporates data from the lumbar spine and hip joints which excluding the proximal humerus [6]. The Tingart index [7] or the deltoid tuberosity index [8] are widely utilized in clinical practice to assess local bone density using shoulder joint AP X-ray. In a cadaver study, Saitoh confirmed a proportional decrease in bone density of the humeral head and femoral head [9]. However, the association between proximal humerus osteoporosis and DXA remains unclear.

While bone density testing is widely used, its availability remains limited in certain underprivileged healthcare settings, necessitating the exploration of alternative reliable methodologies for preliminary screening. Numerous researchers have dedicated their efforts to addressing this challenge. For example, Gabriela utilized machine learning techniques to develop a predictive model for osteoporosis using electromagnetic waves [10], reducing the need for unnecessary DXA tests and conserving public health resources in Brazil. Similarly, Sato employed chest X-ray analysis to predict localized rib bone density reduction [11]. This study involved collecting patient data including DXA scans and proximal humerus X-rays which were then leveraged with machine learning algorithms to adapt Tingart's approach into a straightforward decision support system capable of correlating with bone density while forecasting osteoporosis severity within the proximal humerus.

2. Materials and methods

2.1. Inclusion and exclusion criteria

Inclusion criteria: (1) Patients with proximal humerus fractures, (2) Patients undergoing arthroscopic rotator cuff repair, (3) Patients with hip fractures. Exclusion criteria: (1) Pregnant or lactating women, (2) History of traumatic surgery on the lumbar spine, bilateral hips, or shoulders involving the placement of artificial prostheses or implants, (3) Presence of tumors or other factors leading to secondary osteoporosis, (4) Prolonged bed rest or insufficient physical activity, (5) Brachial plexus injury resulting in upper limb dysfunction, (6) Incomplete clinical and imaging data.

2.2. General information

A retrospective random selection of 102 inpatients from January 2021 to January 2023 was conducted. After applying the inclusion criteria, 5 cases were excluded, consisting of 2 cases with previous surgical history, 2 tumor patients, and 1 case with incomplete patient data. The study finally included 97 patients, with an average age of 73.0 ± 13.6 years (range: 43–98 years), including 21 male patients (21.6 %) and 76 female patients (78.4 %). The overall BMI was 22.8 ± 3.68 (kg/m2). Among them, there were 24 cases of proximal humerus fractures, 52 cases of rotator cuff injuries, and 22 cases of hip fractures. Patients were grouped based on bone density assessment, with 25 cases having normal bone mass, 35 cases with osteopenia, and 37 cases with osteoporosis. Basic data within each group were summarized and statistically analyzed (Table 1). This study has received approval from the Medical Research Ethics Committee of the hospital(2019–64), and all participants have provided informed consent by signing appropriate forms.

Table 1.

Basic information of patients.

 Summary
 Normal
 Osteopenia
 Osteoporosis
 p.overall
N = 97 N = 25 N = 35 N = 37
Gender <0.001
Female 76 (78.4 %) 12 (48.0 %) 29 (82.9 %) 35 (94.6 %)
Male 21 (21.6 %) 13 (52.0 %) 6 (17.1 %) 2 (5.41 %)
Age 73.0 (13.6) 60.7 (10.2) 72.1 (11.9) <0.001 <0.001
BMI 22.8 (3.68) 24.9 (3.68) 22.7 (2.92) 21.4 (3.77) 0.001
Open in a new tab

2.3. Methods

Prior to the surgical procedure, all patients underwent shoulder joint AP X-rays and bone density tests. Subsequently, the patients were categorized into three groups based on the findings of the bone density test: normal(1<T < −1),osteopenia(-1<T < −2.5), osteoporosis(T < −2.5)(Fig. 1). Employing the approach developed by Markus J. Tingart's method [7], and the diagnostic imaging processing software - Medraw Print developed by Imaging Medical Technology (Shanghai) Co., Ltd. was used to read the DICOM images of patients' shoulder joint X-rays. Two segments of data were selected for measurement. The first segment was measured from the midshaft of the humerus to the same cortical thickness on the diaphysis, and the outer and inner widths of the diaphysis were measured (M1, M2). The second segment was selected 2 cm away from the first segment horizontally, and the widths of the inner and outer sides were also measured (M3, M4) (Fig. 2, Fig. 3). To avoid differences between image values and real data, a ratio-based approach was adopted. Four groups of values were combined and defined as follows: ratio1 = (M1 - M2)/(M3 - M4); ratio2 = (M1 - M3)/(M2 - M4); ratio3 = (M1/M2); ratio4 = (M1/M3); ratio5 = (M1/M4); ratio6 = (M2/M3); ratio7 = (M2/M4); ratio8 = (M3/M4).

Fig. 1.

Fig. 1

Open in a new tab

Patient bone mineral density Report.

Fig. 2.

Fig. 2

Fig. 2

Open in a new tab

a: Measurement of M1 and M2 using the software.

Fig. 2b: Measurement of M3 and M4 using the software.

Fig. 3.

Fig. 3

Fig. 3

Open in a new tab

a: Patient's values for M1 and M2.

Fig. 3b: Patient's values for M3 and M4.

Based on the Gini index, a decision tree was constructed using the clinical radiological X-ray measurement data in combination with patient bone density indicators [12,13]. The machine was trained using deep learning and screening to generate diagnostic criteria. The 97 patients were randomly sampled in a stratified manner at a ratio of 6:4, resulting in a training dataset (n = 59) and a test dataset (n = 38). The training set was used to construct the decision tree, while the test set was used to evaluate the performance of the decision tree (Fig. 4). To validate the variables selected by the decision tree model, multinomial logistic regression was performed to assess the correlation between the selected variables and osteoporosis.

Fig. 4.

Fig. 4

Open in a new tab

Employing a decision tree approach for data visualization.

2.4. Evaluation metrics

The evaluation metrics include patient age, gender, height, weight, bone density indicators, and imaging measurement parameters. The collection and analysis of the above information were decided upon through consultation with the same group of doctors and evaluated based on actual clinical conditions.

2.5. Statistical methods

Categorical variables are described as counts (percentages), while continuous variables are described as means (standard deviations) or medians [25th percentile, 75th percentile]. Differences between variables in different groups were compared using one-way analysis of variance or Kruskal-Wallis test for continuous variables and chi-square test for categorical variables. A decision tree based on the Gini index was constructed to select clinical indicators and generate diagnostic criteria based on the selected clinical indicators. The 97 patients were stratified randomly in a 6:4 ratio to form training (n = 59) and test (n = 38) datasets. The training dataset was used to build the decision tree model, and the test dataset was used to evaluate the performance of the decision tree. The relevant evaluation indicators for each outcome classification prediction were calculated, including sensitivity, specificity, positive predictive value, and negative predictive value, using the model's predicted results (using osteoporosis as an example). Finally, multinomial logistic regression was used to assess the correlation between the selected variables by the decision tree model and osteoporosis, thus validating the rationale for selecting these variables.

3. Results

3.1. General information

Among the 97 patients, they were grouped based on bone density, with 25 cases having normal bone mass, 35 cases with osteopenia, and 37 cases with osteoporosis. There were 21 male patients (21.6 %) and 76 female patients (78.4 %), with a significantly higher proportion of female patients. The average age of the patients was 73.0 ± 13.6 years (range: 43–98 years), and the average BMI was 22.8 ± 3.68 (kg/m2). There were statistically significant differences in age and BMI values among the normal, osteopenia, and osteoporosis groups, with advanced age and lower BMI more common in the osteoporosis group (Table 1).

3.2. Establishment of decision tree model

Different combinations of values obtained from the patients' proximal humerus images were input in sequential order, and most of the values were found to have statistically significant differences in conventional bone density classifications (Table 2). Based on the Gini coefficient calculation of the training dataset (n = 59), a decision tree was initially grown with all variables included, and then pruned multiple times based on CP values to obtain the final decision tree model, which was found to be only related to ratio7 (Fig. 5). Additionally, the classification of patient age and bone density in the final decision tree model was analyzed and found to be consistent with current clinical knowledge (Fig. 6).

Table 2.

Statistical significance of different parameters with bone density classification.

Parameters
 [ALL]
 Normal
 Osteopenia
 Osteoporosis
 p. overall
N = 97 N = 25 N = 35 N = 37
ratio1 0.93 (0.11) 0.89 (0.08) 0.92 (0.10) 0.96 (0.14) 0.053
ratio2 0.84 [0.71; 0.97] 0.80 [0.68; 0.86] 0.84 [0.75; 0.93] 0.92 [0.76; 1.10] 0.048
ratio3 1.30 (0.07) 1.33 (0.06) 1.31 (0.06) 1.27 (0.08) 0.005
ratio4 1.13 (0.05) 1.12 (0.05) 1.13 (0.04) 1.12 (0.06) 0.772
ratio5 1.57 (0.14) 1.63 (0.11) 1.61 (0.13) 1.50 (0.16) 0.001
ratio6 0.86 [0.83; 0.91] 0.84 [0.81; 0.87] 0.85 [0.83; 0.92] 0.87 [0.85; 0.92] 0.038
ratio7 1.21 (0.08) 1.23 (0.07) 1.23 (0.07) 1.18 (0.09) 0.028
ratio8 1.40 (0.11) 1.45 (0.08) 1.42 (0.10) 1.34 (0.10) <0.001
Open in a new tab

Fig. 5.

Fig. 5

Open in a new tab

Decision tree.

Fig. 6.

Fig. 6

Open in a new tab

Distribution of age, bone density classification, and Ratio7 in the decision tree model.

3.3. Performance evaluation of the decision tree model

The final decision tree constructed using the training dataset was evaluated using the test dataset (n = 38). The model's predictive results on the test dataset are shown in Table 3. The accuracy of the model on the test dataset was 0.7895 (95 % CI: 0.6268, 0.9045), which showed a significant difference compared to noninformation rate (0.3684) (0.7895 > 0.3684, p < 0.001). The sensitivity, specificity, and other evaluation metrics of the model's predictions for each outcome classification are shown in Table 4.

Table 3.

Model predictive results on test dataset.

Normal (True) Osteopenia(True) Osteoporosis (True)
Normal (Predicted) 10 1 0
Osteopenia (Predicted) 0 9 3
Osteoporosis (Predicted) 0 4 11
Open in a new tab

Table 4.

Performance metrics of the decision tree model.

Sensitivity Specificity Positive Predictive Value (PPV) Negative Predictive Value (NPV)
Normal 1 0.9643 0.9091 1
Osteopenia 0.6429 0.875 0.75 0.8077
Osteoporosis 0.7857 0.8333 0.7333 0.8696
Open in a new tab

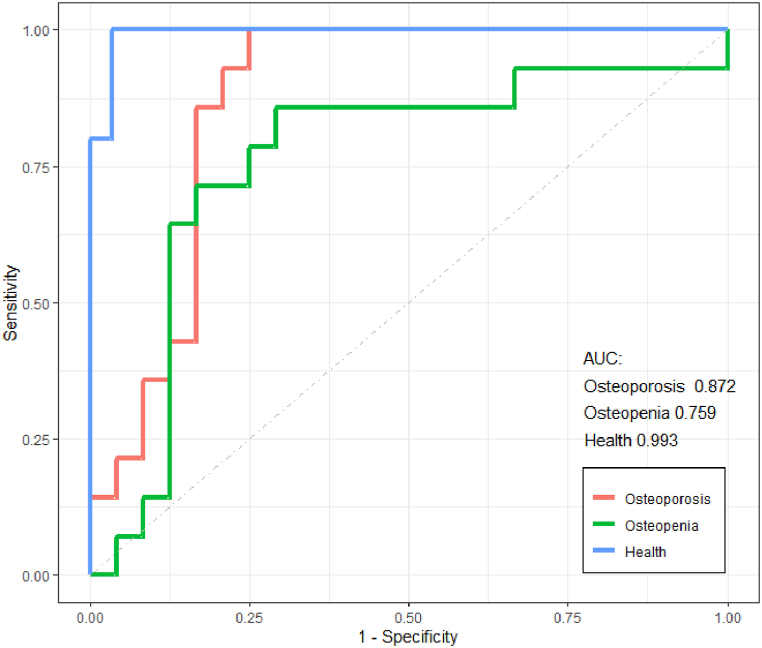
Fig. 7 displays the ROC curves and the area under the curve (AUC) for each outcome classification, with AUC values of 0.993, 0.759, and 0.872 for Normal, Osteopenia, and Osteoporosis, respectively. This indicates that the model is effective in identifying osteoporosis patients based on the measurement of proximal humerus X-rays.

Fig. 7.

Fig. 7

Open in a new tab

Roc curves for sensitivity and specificity of the decision tree model.

3.4. Validation of the decision tree model

Multiple logistic regression was employed to validate the correlation of various factors with osteoporosis and osteopenia in the machine-learning-based decision tree model. It was found that the ratio7 (M2/M4), age, and gender showed statistically significant differences with osteoporosis and osteopenia. However, there was no statistically significant difference observed between BMI values and osteoporosis or osteopenia in this study (Table 5).

Table 5.

Multinomial logistic regression analysis.

Outcome Predictor Odds Ratio (95 % CI) p-value
Osteopenia Intercept
Osteopenia ratio7 ≥ 1.13 0.04 [0.0015, 1.0036] 0.0503
Osteopenia 64 ≤ age <83 9.11 [3.45, 105.96] 0.0007
Osteopenia age ≥83 26.58 [2, 353.26] 0.0127
Osteopenia sex M 0.10 [0.02, 0.49] 0.0047
Osteopenia BMI 0.84 [0.67, 1.05] 0.1330
Osteoporosis Intercept
Osteoporosis ratio7 ≥ 1.13 0.003 [0.00, 0.12] 0.0018
Osteoporosis 64 ≤ age <83 75.19 [3.82, 1479.12] 0.0044
Osteoporosis age ≥83 812.41 [24.81, 26603.55] 0.0002
Osteoporosis sex M 0.02 [0.00, 0.26] 0.0026
Osteoporosis BMI 0.79 [0.61, 1.02] 0.0757
Open in a new tab

Patients with a Ratio7 (M2/M4) ≥ 1.13 have a lower likelihood of developing osteoporosis compared to those with Ratio7 (M2/M4) < 1.13 (OR 0.003 [0.00, 0.12], p = 0.0018). In other words, patients with Ratio7 (M2/M4) < 1.13 are at a higher risk of developing osteoporosis. Compared to patients under 64 years old, those between 64 and 83 years old (OR 19.11 [3.45, 105.96], p = 0.0007; OR 75.19 [3.82, 1479.12], p = 0.0044) and patients above 83 years old (OR 26.58 [2, 353.26], p = 0.0127; OR 812.41 [24.81, 26603.55], p = 0.0002) have a higher risk of experiencing osteopenia and osteoporosis. Furthermore, compared to females, males have a lower risk of osteopenia and osteoporosis (OR 0.10 [0.02, 0.49], p = 0.0047; OR 0.02 [0.00, 0.26], p = 0.0026).

4. Discussion

4.1. Proximal humerus fractures and Regional bone mineral density

Humeral proximal fractures are a prevalent occurrence among the elderly, ranking second only to hip and distal radius fractures in terms of incidence rate [14]. Carbone's retrospective study revealed that 72.4 % of patients with humeral proximal fractures had osteoporosis. Moreover, specific fracture types such as diaphyseal comminution, compression of fracture fragments, condylar comminution, and subluxation are frequently observed in individuals with osteoporosis [15].

Treatment of proximal humerus fractures often involves consideration of multiple factors, with the majority being managed conservatively. A study involving 160,000 patients aged over 65 with proximal humerus fractures from 2010 to 2019 found that 17 % underwent surgical treatment while 83 % opted for conservative management. Randomized clinical trials have also indicated comparable treatment outcomes between the two approaches [16,17]. However, for displaced fractures, surgical intervention remains the preferred method. In younger patients with good bone quality, complications related to internal fixation failure during surgery are rare; however, elderly patients with osteoporosis exhibit a significantly higher incidence of such complications [4]. Consequently, due to the impact of osteoporosis, there has been a notable shift in surgical approach selection over the past decade: plate fixation and intramedullary nail fixation decreased by 25.7 % and 81.9 %, respectively, while reverse shoulder arthroplasty increased by 1841.4 %. This trend warrants attention [18].

Currently, the challenge perplexing shoulder joint surgeons lies in the absence of a standardized method for assessing bone density in the proximal humerus. While bone density measurement is currently based on assessments of lumbar spine and femoral head bone density, which provide an overall indication of bodily condition, there lacks a consistent evaluation standard for other regions of bone density. In a 1993 comparative study by Japanese scholar Satoru Saitoh [9], it was demonstrated that the bone density in the proximal humerus is approximately two-thirds lower than that in the corresponding region of the femoral head; notably, the highest bone density is found at the top of the humeral head, while the neck exhibits roughly half this density with only one-third of trabecular bone stress resistance compared to that at the head. Furthermore, women over 60 years old generally exhibit lower femoral head bone density compared to men. In 2003, Dr. Markus J. Tingart of Harvard Medical School in the United States presented his unique findings in the British edition of JBJS. He introduced the Tingart index, a method for predicting proximal humeral bone density using X-rays, and determined that the average cortical bone density was 4.4 ± 1.0 mm. Furthermore, he observed a significant difference in cortical bone thickness between patients under 70 and those over 70 [7].

Drawing inspiration from the forementioned articles, the author employed Tingart's method to analyze X-ray images and categorized the measured values into three segments representing normal bone density, reduced bone density, and osteoporosis based on a comparison with traditional bone density indicators. In refining Tingart's measurement approach, the author introduced a proportional-based method to mitigate errors arising from differences between actual values and pixel-based measurements in images. This endeavor aims to identify a straightforward, dependable, and viable means of assessing proximal humerus bone density. The author also observed numerous studies on osteoporosis assessment in the proximal humerus and diverse evaluation criteria; however, there remains ambiguity regarding their correlation with osteoporosis severity (bone density) as well as predictive trends. Notably in 2020, Norio utilized machine learning to assess the relationship between hip imaging and osteoporosis [19]. Similarly in 2022, Yoichi et al. validated the potential for predicting bone density through chest X-rays using deep learning [11]. This study leveraged machine learning techniques to process measured data, thereby enhancing result reliability.

4.2. Applications of machine learning

The name machine learning was proposed in 1959 by the famous computer scholar Arthurs Samuel [20]. Mainly by introducing algorithms, ingesting input data, applying computer analysis to predict output values within an acceptable accuracy range, identifying patterns and trends in the data, and ultimately learning from previous experience [21,22]. Traditional statistics are largely based on testing causal hypotheses and selecting models around significance and in-sample goodness of fit. Machine learning is less concerned with the interpretability of models and more mathematically concerned with the predictive performance of models and the generalization around cross-validation and iterative improvement of algorithms [23]. With the development of computer science, machine learning is also introduced into medicine, which is mainly applied in the prediction, diagnosis, and treatment of diseases [[24], [25], [26], [27], [28], [29], [30]]. Salgado [5] and other scholars used machine learning to study whether patients in ICU need vasopressors, and predicted the steps according to 24 clinical indicators in ICU, achieving certain success. Japanese scholar Sato [11] proposed that osteoporosis patients could be screened by predicting bone mineral density of chest radiographs through the study of chest X-ray and T-value score of bone mineral density using machine learning methods. In addition, Hsieh [30] and other scholars also carried out bone mineral density prediction and fracture risk assessment of patients through the method of machine learning. Based on such ideas, we developed an integrated machine learning model based on proximal humerus radiographs, age, gender, and BMI to predict bone mineral density (g/cm2) and diagnosis based on T-values (normal, osteopenia, osteoporosis). In terms of performance, the area AUG under the prediction curve of normal, osteopenia and osteoporosis was 0.993, 0.759 and 0.872, respectively (Fig. 7). The results show that this model is suitable for screening patients with osteoporosis by X-ray measurement of proximal humerus.

Decision trees are a class of machine learning algorithms based on clinical, detection or radiological data [31]. Initially, decision trees were built using clinical evidence and making recommendations based on a variety of data sources and expert opinions. However, with the advent of the era of big data, the amount and complexity of data are constantly increasing, so it is necessary to construct and divide decision tree variables through computer-aided methods [32]. Since the amount of data is greatly increased by multiple measurements, machine learning may be an effective way to establish prediction intervals. On the one hand, machine learning models such as decision trees make it easier to get interpretable results and determine potential relationships between multiple outcomes. On the other hand, machine learning can also be used as a tool for data mining, providing new ideas for diagnosis and treatment. In the choice of variables, in general, obesity is a protective feature of osteoporosis, which provides mechanical stimulation to the bones [33]. The model established by Bogyeong [26] through deep learning also determined the relationship between obesity and bone density as linear. Although our model also shows that BMI values are statistically different in the normal population, in people with bone loss, and in people with osteoporosis. However, in the calculation process of decision tree, BMI is not used as a screening indicator, mainly variables such as age and gender have better performance in the classification process. The advantage of this study is that the shoulder joint X-ray is a routine examination that accurately reflects a person's true anatomy, and the measurement parameters are derived from the shoulder joint. Unlike the DXA data of the hip and spine, these data can better reflect the local bone mass of the proximal humerus.

5. Limitation

In clinical practice, the Tingart index is often interfered with because of the fracture line of the proximal humerus. Part of the data in this study were collected from measurements of the proximal end of the contralateral humerus. Of course, Christian Spross [8] et al. proposed to use deltoid Tuberosity index as an index to measure local osteoporosis and believed that if its ratio was less than 1.4, local osteoporosis could be considered. Secondly, as a preliminary exploration, this study still has shortcomings in the number of cases, but the decision tree through machine learning has shown effectiveness, and more information will be collected in the future to improve the credibility. Finally, in the measurement of image data, more software or AI programs can be tried to optimize.

6. Conclusion

This study demonstrates the reliability of utilizing X-ray characteristics of the proximal humerus as a basis for osteoporosis screening through machine learning. The results from the test set indicate accurate classification of osteoporosis, bone loss, and normal populations. Furthermore, verification with the test set confirms high accuracy of this method, rendering it interpretable and applicable to real-world evaluation. Consequently, our study presents an effective and convenient approach for clinicians to screen for osteoporosis and predict bone mass in the proximal humerus.

CRediT authorship contribution statement

Gen Li: Writing – original draft. Nienju Wu: Formal analysis. Jiong Zhang: Visualization, Investigation. Yanyan Song: Investigation. Tingjun Ye: Writing – review & editing. Yin Zhang: Software. Dahang Zhao: Supervision. Pei Yu: Formal analysis, Conceptualization. Lei Wang: Supervision. Chengyu Zhuang: Visualization, Validation, Supervision, Software, Resources, Funding acquisition, Formal analysis, Data curation, Conceptualization.

Declaration of Competing interest

The authors declared no potential conflicts of interest with respect to the research, authorship, publication of this article.

Footnotes

☆

This work was supported by:National Key Research and Development Program of China (2021YFB3200603), Shanghai Special Research Project on Aging and Maternal and Child Health(2020YJZX0126), National Natural Science Foundation of China (82102618 and 32171317), Key project of “Star of Jiaotong University” Biomedical Engineering (YG2021ZD06)，Shanghai Municipal Health Commission Fund (202140231).

Contributor Information

Pei Yu, Email: yupei_ortho@163.com.

Lei Wang, Email: ray_wangs@hotmail.com.

Chengyu Zhuang, Email: zhuangchengyu@msn.com.

References

  • 1.Johnell O., Kanis J.A. An estimate of the worldwide prevalence and disability associated with osteoporotic fractures. Osteoporos. Int. 2006;17(12):1726–1733. doi: 10.1007/s00198-006-0172-4. [DOI] [PubMed] [Google Scholar]
  • 2.Tepass A., Blumenstock G., Weise K., et al. Current strategies for the treatment of proximal humeral fractures: an analysis of a survey carried out at 348 hospitals in Germany, Austria, and Switzerland. J. Shoulder Elbow Surg. 2013;22(1):e8–e14. doi: 10.1016/j.jse.2012.04.002. [DOI] [PubMed] [Google Scholar]
  • 3.Gradl G., Dietze A., Arndt D., et al. Angular and sliding stable antegrade nailing (Targon PH) for the treatment of proximal humeral fractures. Arch Orthop Trauma Surg. 2007;127(10):937–944. doi: 10.1007/s00402-007-0425-5. [DOI] [PubMed] [Google Scholar]
  • 4.Court-Brown C.M., Mcqueen M.M. The relationship between fractures and increasing age with reference to the proximal humerus. Curr Orthopaed. 2002;16(3):213–222. [Google Scholar]
  • 5.Salgado C.M., Vieira S.M., MendonçA L.F., et al. Ensemble fuzzy models in personalized medicine: application to vasopressors administration. Eng. Appl. Artif. Intell. 2016;49:141–148. [Google Scholar]
  • 6.Spross C., Zeledon R., Zdravkovic V., et al. How bone quality may influence intraoperative and early postoperative problems after angular stable open reduction-internal fixation of proximal humeral fractures. J. Shoulder Elbow Surg. 2017;26(9):1566–1572. doi: 10.1016/j.jse.2017.02.026. [DOI] [PubMed] [Google Scholar]
  • 7.Tingart M.J., Apreleva M., VON Stechow D., et al. The cortical thickness of the proximal humeral diaphysis predicts bone mineral density of the proximal humerus. J Bone Joint Surg Br. 2003;85(4):611–617. doi: 10.1302/0301-620x.85b4.12843. [DOI] [PubMed] [Google Scholar]
  • 8.Spross C., Kaestle N., Benninger E., et al. Deltoid tuberosity index: a simple radiographic tool to assess local bone quality in proximal humerus fractures. Clin. Orthop. Relat. Res. 2015;473(9):3038–3045. doi: 10.1007/s11999-015-4322-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Saitoh S., Nakatsuchi Y. Osteoporosis of the proximal humerus: comparison of bone-mineral density and mechanical strength with the proximal femur. J. Shoulder Elbow Surg. 1993;2(2):78–84. doi: 10.1016/1058-2746(93)90004-Z. [DOI] [PubMed] [Google Scholar]
  • 10.Albuquerque G.A., Carvalho D.D.A., Cruz A.S., et al. Osteoporosis screening using machine learning and electromagnetic waves. Sci. Rep. 2023;13(1) doi: 10.1038/s41598-023-40104-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Sato Y., Yamamoto N., Inagaki N., et al. Deep learning for bone mineral density and T-score prediction from chest X-rays: a multicenter study. Biomedicines. 2022;10(9) doi: 10.3390/biomedicines10092323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Breiman L.F.J.H.O.R.A. Routledge; New York: 1984. Classification and Regression Trees. [Google Scholar]
  • 13.Przybyla-Kasperek M., Kusztal K. New classification method for independent data sources using pawlak conflict model and decision trees. Entropy. 2022;24(11) doi: 10.3390/e24111604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Court-Brown C.M., Caesar B. Epidemiology of adult fractures: a review. Injury. 2006;37(8):691–697. doi: 10.1016/j.injury.2006.04.130. [DOI] [PubMed] [Google Scholar]
  • 15.Carbone S., Mezzoprete R., Papalia M., et al. Radiographic patterns of osteoporotic proximal humerus fractures. Eur. J. Radiol. 2018;100:43–48. doi: 10.1016/j.ejrad.2017.12.025. [DOI] [PubMed] [Google Scholar]
  • 16.Olerud P., Ahrengart L., Ponzer S., et al. Internal fixation versus nonoperative treatment of displaced 3-part proximal humeral fractures in elderly patients: a randomized controlled trial. J. Shoulder Elbow Surg. 2011;20(5):747–755. doi: 10.1016/j.jse.2010.12.018. [DOI] [PubMed] [Google Scholar]
  • 17.Fjalestad T., Hole M.O. Displaced proximal humeral fractures: operative versus non-operative treatment--a 2-year extension of a randomized controlled trial. Eur. J. Orthop. Surg. Traumatol. 2014;24(7):1067–1073. doi: 10.1007/s00590-013-1403-y. [DOI] [PubMed] [Google Scholar]
  • 18.Patel A.H., Wilder J.H., Ofa S.A., et al. Trending a decade of proximal humerus fracture management in older adults. JSES Int. 2022;6(1):137–143. doi: 10.1016/j.jseint.2021.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Yamamoto N., Sukegawa S., Kitamura A., et al. Deep learning for osteoporosis classification using hip radiographs and patient clinical covariates. Biomolecules. 2020;10(11) doi: 10.3390/biom10111534. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Shaw D., Samuel A. Medical administration in psychiatric hospitals. Lancet. 1959;2(7095):170–172. doi: 10.1016/s0140-6736(59)90576-8. [DOI] [PubMed] [Google Scholar]
  • 21.DE Santis M., Rinaldi F., Falcone E., et al. Combining optimization and machine learning techniques for genome-wide prediction of human cell cycle-regulated genes. Bioinformatics. 2014;30(2):228–233. doi: 10.1093/bioinformatics/btt671. [DOI] [PubMed] [Google Scholar]
  • 22.Joshi A., Ramakrishman N., Houstis E.N., et al. On neurobiological, neuro-fuzzy, machine learning, and statistical pattern recognition techniques. IEEE Trans Neural Netw. 1997;8(1):18–31. doi: 10.1109/72.554188. [DOI] [PubMed] [Google Scholar]
  • 23.Ringner M. What is principal component analysis? Nat. Biotechnol. 2008;26(3):303–304. doi: 10.1038/nbt0308-303. [DOI] [PubMed] [Google Scholar]
  • 24.Kourou K., Exarchos T.P., Exarchos K.P., et al. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015;13:8–17. doi: 10.1016/j.csbj.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Yang Y., Xu L., Sun L., et al. Machine learning application in personalised lung cancer recurrence and survivability prediction. Comput. Struct. Biotechnol. J. 2022;20:1811–1820. doi: 10.1016/j.csbj.2022.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Suh B., Yu H., Kim H., et al. Interpretable deep-learning approaches for osteoporosis risk screening and individualized feature analysis using large population-based data: model development and performance evaluation. J. Med. Internet Res. 2023;25 doi: 10.2196/40179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Xu G., Wang D., Zhang H., et al. Prediction of osteoporosis from proximal femoral cortical bone thickness and Hounsfield unit value with clinical significance. Front Surg. 2022;9 doi: 10.3389/fsurg.2022.1047603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Wu X., Zhai F., Chang A., et al. Development of machine learning models for predicting osteoporosis in patients with type 2 diabetes mellitus-A preliminary study. Diabetes Metab Syndr Obes. 2023;16:1987–2003. doi: 10.2147/DMSO.S406695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Bowes M.A., Kacena K., Alabas O.A., et al. Machine-learning, MRI bone shape and important clinical outcomes in osteoarthritis: data from the Osteoarthritis Initiative. Ann. Rheum. Dis. 2021;80(4):502–508. doi: 10.1136/annrheumdis-2020-217160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Hsieh C.I., Zheng K., Lin C., et al. Automated bone mineral density prediction and fracture risk assessment using plain radiographs via deep learning. Nat. Commun. 2021;12(1):5472. doi: 10.1038/s41467-021-25779-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Thomas J.B. Advanced cardiac life support (ACLS) algorithms. A powerful decision tree for management of cardiac arrest victims. Can. Crit. Care Nurs. J. 1989;6(4):12–19. [PubMed] [Google Scholar]
  • 32.Podgorelec V., Kokol P., Stiglic B., et al. Decision trees: an overview and their use in medicine. J. Med. Syst. 2002;26(5):445–463. doi: 10.1023/a:1016409317640. [DOI] [PubMed] [Google Scholar]
  • 33.Cao J.J. Effects of obesity on bone metabolism. J. Orthop. Surg. Res. 2011;6:30. doi: 10.1186/1749-799X-6-30. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Heliyon are provided here courtesy of Elsevier

RESOURCES