Abstract
Experimental studies have shown that ultrasonic cavitation can reversibly open the blood–brain barrier (BBB) to assist drug delivery. Nevertheless, the majority of the present study focused on experimental aspects of BBB opening. In this study, we developed a three-bubble-liquid-solid model to investigate the dynamic behavior of multiple bubbles within the blood vessels, and elucidate the physical mechanism of drug molecules through endothelial cells under ultrasonic cavitation excitation. The results showed that the large bubbles have a significant inhibitory effect on the movement of small bubbles, and the vibration morphology of intravascular microbubbles was affected by the acoustic parameters, microbubble size, and the distance between the microbubbles. The ultrasonic cavitation can significantly enhance the unidirectional flux of drug molecules, and the unidirectional flux growth rate of the wall can reach more than 5 %. Microjets and shock waves emitted from microbubbles generate different stress distribution patterns on the vascular wall, which in turn affects the pore size of the vessel wall and the permeability of drug molecules. The vibration morphology of microbubbles is related to the concentration, arrangement and scale of microbubbles, and the drug permeation impact can be enhanced by optimizing bubble size and acoustic parameters. The results offer an extensive depiction of the factors influencing the blood–brain barrier opening through ultrasonic cavitation, and the model may provide a potential technique to actively regulate the penetration capacity of drugs through endothelial layer of the neurovascular system by regulating BBB opening.
Keywords: Blood–brain barrier, Multiple bubbles, Drug delivery, Finite element method (FEM)
1. Introduction
When the ultrasonic energy reaches a certain threshold, the cavitation nucleus will vibrate and grow continuously under ultrasonic excitation, which is the common ultrasonic cavitation effect in the application of ultrasonic wave [1], [2]. The bubble will produce high-pressure and high-temperature during the oscillation process, and with the generation of shock wave and micro jet, which will produce corresponding mechanical effects on the surrounding objects [3], [4]. Nowadays, cavitation effect is widely used in various fields, such as drug delivery [5], [6], chemical reaction [7], [8], fouling cleaning [9], [10] and water treatment [6], [8]. With the advancement of medical technology, ultrasound-driven microbubbles have attracted the attention of medical practitioners due to ultrasound imaging and other technologies. Studies have shown that moving bubbles can cause oscillation or even damage nearby tissues [11], [12]. However, the effect of bubble motion constrained in blood vessels may be beneficial under appropriate ultrasonic excitation [13], [14], [15], [16], [17], including affecting the permeability of blood vessel walls [13], [14], dredging the blood–brain barrier (BBB) [14], [15], and recanalization of blocked blood vessels [16], [17]. It is necessary to explore bubble dynamics for the application of bubbles, especially the effectiveness and safety of focused ultrasound-induced BBB opening. At present, most drugs developed for the treatment of nervous system diseases cannot pass through BBB at therapeutic concentration. The emergence of ultrasonic cavitation is the bottleneck to achieve the therapeutic effect of drugs in the brain [18], [19].
Numerous experiments have been conducted to investigate the viability and efficiency of the use of ultrasonic cavitation to open BBB. The results have shown that during focused ultrasound (FUS) treatment, the BBB can be safely and reversibly opened with the assistance of bubbles [18], [20], [21], [22], which can enhance the permeability of the blood–brain barrier [21] and deliver targeted drugs to the treatment point [21]. The feasibility of this treatment method has been confirmed in the treatment of patients with Parkinson’s disease (PD), Alzheimer’s disease and amyotrophic sclerosis [21]. In order to study whether submicron bubbles can compress BBB when oscillating at their resonant frequencies, Fan et al. [20] conducted experiments on rat brains in vitro, the results showed that it can greatly limit inertial cavitation, enhance stable cavitation, and reduce the extravasation of red blood cells [20]. In a mouse model of Alzheimer ‘s disease, Alison et al. used a two-photon microscopy to study in real time the differences between FUS-induced permeability of plaque-burdened vessels in a mouse model of Alzheimer’s disease compared to healthy vessels in non-transgenic littermates [22]. Choi et al. studied the dependence of FUS-induced BBB opening on bubble size through experiments on mice [23]. Poon et al. proposed an experimental method for intravital multiphoton microscopy using a skull window aligned with an annular transducer and a 20x objective lens [24]. Dallan et al. reported that a significant and destructive inflammatory response was observed at high doses of circulating microbubbles (MBs), and the severity of the response depended on the dose of microbubbles [25]. It is worth noting that the instantaneous destruction of the BBB by focused ultrasound (FUS) can promote non-invasive drug delivery, which can significantly increase the local drug concentration of the targeted tissue to 60 times [20], with precise spatial and temporal specificity [18]. Yan et al. opened the BBB by low-intensity focused ultrasound (LIFU) and delivered curcumin-loaded Lipid-PLGA hybrid nanobubbles (Cur-NBs) to the targeted tissue in the mouse brain [26], the results showed that the transmission efficiency and therapeutic efficiency of curcumin in mice were greatly improved [26]. The central nervous system (CNS) is the preferred target for the treatment of brain diseases, but it is also one of the most difficult organs for drugs to reach the target [27]. With the assistance of FUS and microbubbles, Felix et al. successfully delivered therapeutic agents to the CNS, which was confirmed by in vivo mouse experiments [27]. Ting et al. used FUS to destroy BBB and used loading tools to deliver drugs at targeted sites, the results showed that this method not only slowed down the degradation rate of drugs, but also increased the deposition of drugs at targeted sites [28]. Deng et al. found that ultrasound-assisted delivery of drugs through the BBB can greatly improve the therapeutic effect of brain neurological diseases [29]. High intensity focused ultrasound as a non-invasive in-vitro method has received great attention in clinical practice.
Studies have shown that the BBB is mainly opened by steady-state cavitation [20]. In terms of numerical research, many studies have simulated the dynamic behavior of bubbles trapped in blood vessels and the effect of bubble motion on surrounding tissues [13], [30], [31], [32], [33], [34]. Liu et al. established a bubble-fluid–solid model to study the biomechanical effects of ultrasound-driven microbubbles (UDM) on microvessels, and evaluated the effects of various acoustic parameters and tissue parameters, the results show that the blood vessel wall will be convex or concave while the microbubble vibrates, and the results are directly related to the ultrasonic frequency, the blood vessel radii and the initial microbubble radius [13]. Nazanin et al. established a bubble-fluid-container model and evaluated the influencing factors of wall stress based on the Marmottant shell model, the results show that wall stress is related to ultrasonic frequency and bubble volume [30]. Xie et al. established a two-way coupling model of bubble-vascular system and combined with experimental results, the damage mechanism of ultrasonic cavitation on vascular wall was discussed in depth [31]. Hosseinkhah et al. established a mathematical model of the bubble-vascular system, and discussed the influence of the symmetric and asymmetric distribution of bubbles on the model results [32]. Wiedemair et al. built a coupled, multi-domain numerical model using the finite volume formulation to study the interaction between microbubbles and closed capillaries [33]. Miao et al. [34] studied the excitation-response of ultrasound-induced bubbles to the vessel wall using an axisymmetric finite element model, the simulation results show that the stretching part of the vascular wall plays a decisive role in the ruptured vascular wall during ultrasonic excitation, the tissue characteristics and ultrasonic characteristics have an important influence on the results [34]. Chen et al. explored the response of a single bubble in a microcontainer filled with viscous fluid, and evaluated the effects of vessel size, acoustic parameters, and viscoelasticity of the microbubble shell on bubble motion and surrounding containers [35].
The above results show that the ultrasonic-induced cavitation effect has important research prospects in opening blood–brain barrier, but most of the studies are analyzed in vitro experiments [26], [27], [28], [29], or they investigated the effect of individual bubbles and did not take into account the inter-bubble forces [13], [31], [32], [33], there are also some studies [36], [37], [38], [39], [40] on the correlation between multiple microbubbles in existing research. For example, Mirsandi et al. report [36] demonstrated the interaction of two bubbles in a viscous fluid, and primarily examined the influence of parameters like the Reynolds number on bubble motion. The kinetic behavior of two bubbles rising side by side in an incompressible liquid was experimentally studied by Meenu et al [37]. Wang et al. [38] addressed the dynamics of discontinuous wave-driven double bubble and discussed the effect of acoustic parameters on the bubble dynamics in depth. Liang et al. [39] developed a new system of equations to study the bubble dynamics behavior of three bubbles distributed on a straight line. Wu et al. [40] developed a kinetic model to describe the aspherical oscillations of three bubbles with a linear distribution. However, the majority of current multibubble research has focused primarily on double-bubble models [2], [36], [37], [38], and described the dynamics behavior of two bubbles in an infinite domain environment in terms of analytical solutions. The bubbles in the models arrange in a predominantly rectilinear manner, they ignore the forces existing between bubbles by assuming that there is a large space between them [39], [40]. The mechanism of ultrasonic cavitation is not clear. In addition, there are a large number of bubbles in the liquid during the ultrasonic excitation process. At present, there are few studies on the multiple bubbles dynamics in the container. In this paper, we establish a time-varying control model of three-bubble-vascular system. In the process of ultrasonic excitation, we discuss the influence mechanism of microbubbles on BBB by expounding the factors such as stress, displacement and permeability of the model, and deeply analyze the influence of various factors on the model results.
2. Theoretical models and methods
2.1. Theoretical models
In Fig. 1, a three-bubble-vascular system time-varying model is established to analyze the mechanism of ultrasound-induced microbubbles opening the BBB. In the model, three bubbles are evenly distributed on the same plane in an equilateral triangle manner (. The length of the vessel wall is represented by symbol L , and the wall is assumed to be composed of three tissues (The thickness of intima, media and adventitia were 0.3 m, 0.3 m and 0.4 m respectively). In addition, the vascular radius was set to 8 . The origin coordinate of the axis is the leftmost end, and the origin coordinates of the and axes are at the center of the blood vessel wall.
Fig. 1.
A schematic diagram of a bubble–bubble–bubble–blood–vessel system (xy plane).
2.2. Theoretical methods
2.2.1. Conservations of momentum and mass
The blood is assumed to be incompressible, single-phase and uniform Newtonian fluid, and its motion obeys the Navier-Stokes Equation [41] as follows:
| (1) |
| (2) |
Here, , and represent the pressure, density and dynamic viscosity of the liquid, respectively. and are the unit tensor and velocity vector, respectively. The fluid momentum equation, the continuity equation, and the equation of state serve as the primary foundations for the derivation of the Navier-Stokes equation. The Navier-Stokes equations provide information about the evolution of the velocity field over time, the equations of state describe how the pressure and density variations with temperature [42]. Equation (1) satisfies the conservation of mass, Equation (2) is relevant to fluids with low Reynolds coefficients, and shows the link between the fluid’s acceleration, velocity, and pressure.
Assuming that the blood flow at the intake is oriented along the x-axis, and the velocity profile is assumed to be parabolic. The y-axis has zero velocity, the velocity U can be found as follows [43]:
| (3) |
Here, was the steady average velocity at the blood flow entrance, was the radius of the blood vessel.
We assume that the vascular wall is a porous medium material, and the transmural flow in arterial wall is explained by Darcy’s law [41], [44], which describes the relationship between the factors such as permeability and fluid viscosity, and the flow rate of a single-phase fluid through the porous medium, it is important in areas such as the theory of porous media [45]:
| (4) |
| (5) |
Where , and are the vessel inner-wall pressure, the Darcian permeability coefficient, and the velocity of the transmural flow, respectively. It is considered that the vascular wall is made of a porous substance, and the wall porosity’s description is as follows [46]:
| (6) |
Here, the pressure on the vessel wall is represented by , is the proportional constant determined by infame area. is the initial pressure, and its value is 140 mmHg. In order to enable the pressure drop across the vessel wall, we assumes that the constant pressure value is 2333.022 Pa (17.5 mm Hg) at the outer membrane boundary [44].
2.2.2. Solid models and fluid–solid boundaries
This part is an idealistic model based on the presumption of small deformation, satisfying a linear relationship between stress and strain. Solid structure is assumed to be isotropic linear elastic material. In three-dimensional space, the relationship between stress and strain can be described by the following expression under small deformation assumption [47]:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Here, and are Poisson ‘s ratio and Young ‘s modulus, respectively. and are strain components; and are stress components. At the fluid–solid boundary, the following constraints can be written as:
| (13) |
| (14) |
| (15) |
Equations (13)-(15) represent velocity continuity, stress and displacement, respectively. Symbol and represent solid and liquid, respectively.
2.2.3. Bubble dynamics theory
It is assumed that the gas inside the bubble satisfies the ideal gas state equation, the heat transfer is ignored and gas inertia and diffusion are not taken into account because the gas inside the bubble has a lower density and amplitude than blood during the bubble oscillation. Assuming that the bubble is moving in an isothermal manner, we can determine the expression for the gas pressure inside the bubble using the equation of state [48], [49]:
| (16) |
| (17) |
Where , , , and represent the gas pressure inside the bubble, the initial gas pressure inside the bubble, the surface tension of the bubble, the initial static pressure in the liquid and the initial radius of the bubble , respectively. The heat transport and liquid’s compressibility are not taken into consideration in Equation (16). It should be noted that the radius in this paper refers to the effective radius of the bubble. The meaning of is the gas pressure inside the bubble during movement, and γ represents the polytropic exponent of the gas.
At the bubble boundary, the pressure and velocity continuity conditions are followed [50]:
| (18) |
| (19) |
Here, n and k are the unit normal vector and the local curvature of bubble surface, respectively. The rate at the bubble boundary is represented by Equation (18), and the force at the bubble boundary is described by Equation (19).
In addition, the ultrasonic excitation source is expressed by the following Equation [38]:
| (20) |
Where , and represent the amplitude, the frequency of burst and the number of acoustic cycles in the burst, respectively. We assume that the value of is 5.
We know that bubbles interact with each other, and the expression of the radiation sound pressure generated between the two bubbles is as follows [51]:
| (21) |
Where is the radiation sound pressure generated by bubble at the center of bubble , represents the distance between two bubbles. Equation (21) reflects the magnitude of the interaction force between the bubbles.
Based on the above theoretical basis, the secondary Bjerknes force exerted by the (4-i)th bubble to the ith bubble can be expressed [49], [52]:
| (22) |
Here, and are the ith bubble volume and the bubble distance, respectively. The relative position change and nonlinear behavior of the bubbles are reflected in this equation, which indicates whether the bubbles are “near” or “far” from one another at any particular time [52].
2.2.4. Permeability of vessel wall
The research report shows that the wall permeability has a great relationship with the shear stress, and the shape index (SI) of the wall is described by the following expression [53]:
| (23) |
Where is related to the number of mitotic cells per area of 0.64 mm2, is the wall shear stress. In addition, Olgac et al. obtained the following expression by fitting the reference data [54]:
| (24) |
It was assumed that the number of leaky cells correlated with non-mitotic cells is independent on τ. Considering the influence of non-mitotic cells, they improved the Equation (24), and the specific expression is as follows:
| (25) |
The amount of leaky cells in leaky junction area was depended on the following equation:
| (26) |
In Equation (26), denotes the radius of the endothelial cell with a value of 15 μm, and the permeability of the endothelium can be described by the following expression [53]:
| (27) |
| (28) |
| (29) |
Where stands for the fraction of leaky junction, is the permeability of the leaky junction which was related to the , denotes the leaky junction of half-width with a value of 10 nm. In addition, is an invariant constant which can be defined by using known data for [53].
Studies have shown that the unidirectional flux of any compound across the BBB from blood to brain be disposed by the sum of diffusion flux and solvent drag terms [55].
| (30) |
Where is defined as a size-independent volume flux which meaning bulk fluid flow, and its value is 7.3 × 10−5 cm3 s−1 [55]. P is the capillary permeability and its value is 1 × 10−6 cm s−1 [57], is the surface area, is the reflection coefficient of the compound, which depends on its molecular size and on the geometry of the pore [55]. The and are the plasma concentrations and brain parenchyma of the compound, respectively [55] (Taking amoxicillin as an example), we assume that the value of is 3 mmol/L [56]. In this paper, we assume that biological tissue is composed of cylindrical pores of uniform size, is expressed by [55], [58]:
| (31) |
Here, and represent the compound molecular radii and pore radius respectively (Taking amoxicillin as an example, ). The equation illustrates that the effect of penetration of a substance is related to the size of the molecules and the shape of the wall voids (e.g., size, shape). The water conducing porosity, (The values of and are equivalent), within the known range can be described by Carey et al. [59]:
| (32) |
Here, a and b are pore radii, is the number of pores per unit surface area per unit pore radius and its value is 22.6 pores/mm2 [60].
2.2.5. Particle motion equation
The following theory is used to describe the movement of particles based on Section 2.2.4 in order to gain a better understanding of the trajectory and distribution of drug molecules in blood arteries.
| (33) |
| (34) |
| (35) |
| (36) |
Based on Newtonian physics, Equations (33)-(36) represent the kinetic behavior of a particle moving in a fluid and accounts for the fluid’s velocity in addition to additional forces (such as gravity and trailing forces, among others) [61], [62]. is the mass of the particle, is the drag force vector of the particle, () represents the particle size, and represents the density. Note that the influence of gravity is not taken into account here because of the short simulation time and little particle mass. represents the particle’s trailing force vector, which depends on the particle’s mass, velocity, radius, blood velocity, and viscosity. The adhesion condition is adopted by the blood-intima border and the outermost outer membrane boundary, and the bubble-blood flow boundary is set as the elastic boundary condition.
In this paper, we use the finite element method (COMSOL Multiphysics) [35] to solve various physical field equations and various boundary conditions, and the unit size free tetrahedral mesh is used to divide the model. The fluid domain consists of 7922 mesh vertices and 38,327 unit tetrahedrons, respectively. The solid structure consists of 6945 mesh vertices and 30,862 unit tetrahedrons, respectively. In addition, the bubbles are composed of 2279 mesh vertices and 9500 unit tetrahedrons. In order to minimize the influence of the grid on the model results, all models have a minimum unit mass greater than the 0.1 low-quality element restriction, and make the average element mass of all models consistent as much as possible. Furthermore, in every model, there was no alarm phenomenon brought on by a unit mass of less than 0.01. The Navier-Stokes equations are solved on a freely moving deformed mesh, which constitutes the fluid domain. PARDISO solver is used for the coupled system of solid and fluid equations.
3. Numerical results and analysis
3.1. Model validation
To verify the accuracy of the model, we examined the dynamic behavior of bubble in the environment depicted in references [69], [70] using the equations and parameters mentioned above, and contrasted the findings with the results of references. The bubble radius variation over time is shown in Fig. 2(a) from both the simulation and experimental viewpoints, respectively, the lumen inner diameter and bubble spacing in Fig. 2(a) are consistent with the parameters of this paper (, ), and two bubbles in a straight line within the vessel, it should be noted that the effect of the bubble shell is taken into account in references [69], [70]. We calculated the kinetic behavior of the double bubbles in the vessel during 4 cycles using the theory (parts 2.2.1, 2.2.2 and 2.2.3) of this paper, and the major parameters (Fig. 2(b)) are identical to those of references [69], [70] (, , ). Here, we only calculated the situation when the initial radius is 2 m because the difference between the values of the two initial radii is not great. It is discovered that the change rule of the two results is essentially the same, but there are variations, likely as a result of the influence of the bubble shell and other factors. The above results verify the validity of the model in this paper.
Fig. 2.
Bubble radius-time curves under different calculation conditions (Fig. 2(a) is taken from reference [69] and Fig. 2(b) shows the results of this paper).
3.2. Grid and time-step convergence verification
This model must encrypt the bubble region and carefully take into account the time step for obtaining accurate simulation results.
In this part, we describe the radius variation of bubble 3 within 1 s to examine the impact of the time step and the number of units on the simulation results. On the basis of Table 1, the average radius of the bubbles are 1.9932 m at case 1, 1.9932 m at case 2, 1.9933 m at case 3, 1.9934 m at case 4, 1.9944 m at case 5, and 1.9946 m at case 6, respectively. Setting the time step to the first four cases, the results essentially do not differ when the number of meshes in the overall model area is the same. However, when the time step was set to 0.06 μs and 0.1 μs, there was a significant difference in the results, the outcomes demonstrate that the first four cases have greater results precision.
Table 1.
| Name | Parameters | Value (unit) |
|---|---|---|
| Gas polytropic | γ | 1.07 |
| Saturated vapor pressure | 2330 Pa | |
| The initial radius of the microbubble | 2 m | |
| Gas-liquid surface tension | 0.072 N m−1 | |
| The density of blood | 1050 kg m−3 | |
| Sound pressure | 0.4 × 105 Pa | |
| Hemodynamic viscosity | 0.0035 Pa s | |
| The ambient pressure | 1.013 × 105 Pa | |
| Ultrasonic frequency | 1.0 × 106 Hz |
Based on Table 3, the time step is set to 0.02 s, and we meshed the entire area in the model of Fig. 1 using the six cases listed in Table 4. On the basis of Table 1, the average radius of the bubbles are 1.9888 m at case 1, 2.0305 m at case 2, 1.9934 m at case 3, 1.9935 m at case 4, 1.9935 m at case 5, and 1.9935 m at case 6, respectively. The radius change of bubble 3 is essentially insignificant when the number of grids is in the last four cases, but there are clear changes in the findings for the first two grid amounts. Considering the computation time and the precision of the results, the time step and the number of grids in our model are set to 0.02 μs and 78689, respectively.
Table 3.
Time step for case 1, 2, 3, 4, 5, and 6.
| Case | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 0.001 μs | 0.005 μs | 0.01 μs | 0.02 μs | 0.06 μs | 0.1 μs |
Table 4.
Number of units for case 1, 2, 3, 4, 5, and 6.
| Case | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Number of units | 8342 | 44,842 | 78,689 | 136,627 | 144,734 | 204,073 |
3.3. Flow field distribution and particle motion trajectory
The trajectory of drug molecules in blood vessels must be investigated in order to investigate the mechanism of ultrasonic cavitation influencing the admission of drug molecules into the blood–brain barrier. However, considering the large amount of calculation of the three-dimensional model, we use the two-dimensional model to examine the particle’s track in order to reduce the quantity of calculations in this part. We assume that there is a damage boundary on the intima with a length of 10 μm based on Equation (6), which allows the particles to enter the vascular wall at a Darcy velocity of 2 × 10−7 m s−1, In general, the Darcy velocity in the blood–brain barrier is relatively tiny [71], [72], [73], and the values employed in this paper fall within a reasonable range. The findings indicate that the penetration rate is larger and fastest on both sides close to the blood. During the penetration phase, the blood vessel’s maximum Darcy velocity is 1.179 × 10−6 m s−1. Furthermore, the downstream has a rather high particle density, and the particles start to progressively permeate both sides of the blood artery wall. The position length of particles is about 12.7 μm at 2 s, 15.4 μm at 4 s, and 21.1 μm at 10 s, respectively. The penetration rate drops progressively as the particles get deeper, perhaps because the permeability coefficients differ (Fig. 3). It is evident from Equations (30), (31), as well as from pertinent research findings [55], [56], [57], [58], that the penetration impact of pharmacological molecules is typically correlated with both molecular size and wall porosity. Focused ultrasonic waves induce the bubbles' movement to create microjet that causes a comparable amount of stress on the vessel’s wall surface. It is evident from Equation (6) that the bubble motion influences the variation of wall porosity. It is noteworthy that the change in porosity is reversible. The nature of the porosity change may be attributed to the expansion and contraction of the bubbles.
Fig. 3.
Drug molecule distribution and trajectory in blood. The values in the figure represent the Darcy velocity (m s−1) of the particles.
We discuss the impact of single bubble in the blood vessel on blood flow based on the aforementioned bubble dynamics theory. Based on Table 1 and Table 2, the blood flow distribution is depicted in Fig. 4. It is evident that at first, all streamline appears to end at the outlet. However, the streamline’s distribution changes significantly as the bubble moves on, and a back flow phenomena is even seen at the bottom right of the bubble. Furthermore, the bubble will shift downstream and eventually flatten over time, this may be of the tiny amplitude of sound pressure.
Table 2.
| Parameters | Density (kg m−3) | Poisson’s ratio | Young’s modulus (MPa) | Permeability coefficient (m2) |
|---|---|---|---|---|
| Intima | 1000 | 0.49 | 2 × 106 | 2 × 10−16 |
| Media | 1000 | 0.49 | 6 × 106 | 2 × 10−18 |
| Adventitia | 1000 | 0.49 | 4 × 106 | 2 × 10−18 |
Fig. 4.
Intravascular blood distribution. The values in the figure represent the blood velocity (m s−1).
Fig. 5 illustrates the flow of medication molecules in the circulation based on Fig. 4. Assume that at the blood flow’s entrance, 10 particles are expelled at random intervals of very small time. The movement and distribution of drug molecules in 50 μs are depicted in Fig. 5 as a result of ultrasonic cavitation. It can be seen that the particle velocity near the vascular wall is the smallest, and is the easiest to adhere to the vascular wall. Consequently, cavitation bubbles may be employed to modify the particle distribution by altering the liquid’s streamline distribution. Furthermore, it is known from Equation (6) that bubble motion influences the variation in wall porosity, which in turn influences the mobility of drug molecules sticking to the vessel wall. The findings of this study demonstrate that ultrasonic cavitation modifies the fluid flow distribution and wall porosity, which in turn modifies drug molecule penetration. It should be mentioned that this paper only examines the effect of blood flow velocity in Fig. 3, Fig. 4 and Fig. 5.
Fig. 5.
Drug molecule distribution and trajectory in blood. The values in the figure represent the blood velocity (m s−1).
The aforementioned findings indicate that, within the blood flow region, the majority of the particles are concentrated in the region with high fluid velocity, whereas the region with low fluid velocity is more likely to result in the particles adhering to the blood vessel wall. It is possible to exploit the ultrasonic cavitation effect to help the medicine pass through the blood–brain barrier.
3.4. Multi-bubble dynamics analysis
Fig. 6(a) describes the change curve of each bubble radius with time. It can be seen that the movement trends of the three bubbles are almost the same, which may be caused by the bubble distance. It is worth noting that the bubble 3 in the middle is slightly suppressed. In order to further understand the interaction and motion between bubbles, we calculate the secondary Bjerknes force between bubbles based on Equation (22). In Fig. 6(b), we can get the nonlinear behavior between bubbles, such as near and far away [52], which may be caused by inconsistent volume changes. The study shows that when the secondary Bjerknes force is more than zero, the double cavitation bubbles resist one another [52]. Conversely, they attract one another when the secondary Bjerknes force is less than 0, the absolute magnitude of the secondary Bjerknes force indicates the degree of interaction [52].
Fig. 6.
The curve of radius and secondary Bjerknes force with time.
3.5. Biological effect analysis
In the process of ultrasonic excitation, bubble movement will cause fluctuations in the surrounding tissue which can temporarily and reversibly open the BBB of the local tissue [74], [75], [76]. We take half of the blood vessel wall as the research object. The material properties of biological tissue have a great influence on its displacement [67], [68], [77]. Fig. 7 shows the displacement of the vessel wall changes with position in the case of 2 μs, 6 μs and 10 μs. Taking the y-axis direction as the positive direction, one can find that the blood vessel wall is almost in the open state, and the lower blood vessel wall seems to move more than the upper blood vessel wall. At 10 μs, the total displacement (TD) at the center of the blood vessel wall is about 0.114 μm.
Fig. 7.
The displacement-position curve of upper and lower vascular wall.
Under ultrasonic excitation, the shear stress has a great influence on the tissue wall which act as a ‘thrust’ to continuously affect the motion state of the blood vessel wall [78], [79]. Fig. 8 depicts the shear stress-position curves of the upper and lower vessel walls at 2 μs, 6 μs and 10 μs. It can be seen that the shear stress of the wall can not be underestimated, and the bubble motion becomes severe with the extension of time. In fact, the shear stress generated by the bubble motion can reach thousands of pascals, and even megapascals when the bubble is annihilated [80], [81], [82].
Fig. 8.
The shear stress-position curve of upper and lower vascular wall.
In addition, shear stress is one of the important factors affecting the permeability of tissue wall [4], [13]. Fig. 9 shows the permeability-position curves of the wall surface at three moments. It can be seen that the bubble motion becomes more and more intense with the increase of time, and the permeability change in the region near the bubble is the most significant compared to other regions, the reason for this may be found in the results of Fig. 8, in which we can observe that the violent movement of the bubbles causes the wall shear stress values to fluctuate violently, we can know from Equation (23) that the wall permeability causes a corresponding oscillating change. The results show that ultrasonic cavitation has a great influence on the permeability of the tissue wall, and the simulation results are consistent with the relevant research results [4], [13].
Fig. 9.
The permeability-position curve of upper and lower vascular wall.
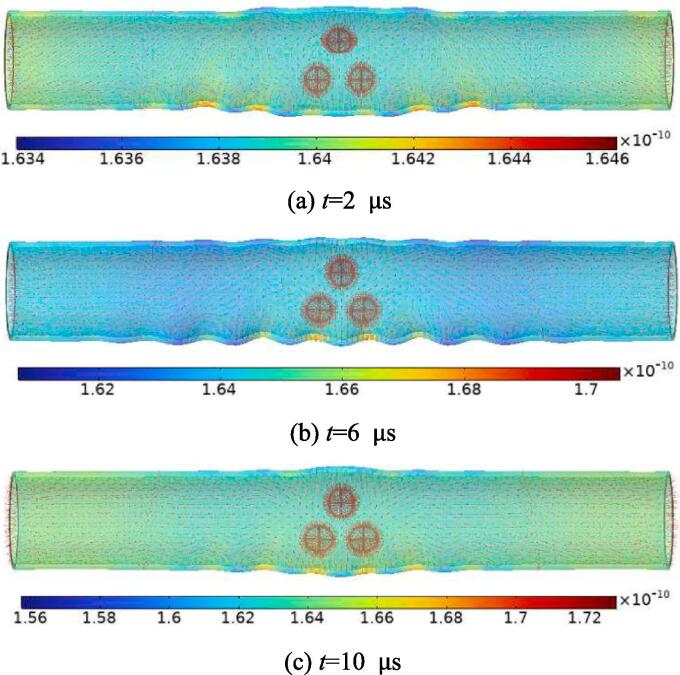
According to the Equation (30), we calculate the unidirectional flux of amoxicillin on the endothelial wall at different times (Fig. 10). It can be seen that ultrasonic cavitation has an effect on the unidirectional flux of the wall surface, and the effect is more obvious with the increase of ultrasonic intensity. The unidirectional flux’s maximum and lowest values are in close proximity to the cavitation area. the maximum unidirectional flux are 1.646 × 10−10 mol s−1 at 2 s, 1.705 × 10−10 mol s−1 at 6 μs, and 1.729 × 10−10 mol s−1at 10 μs, respectively. Compared with the non-cavitation effect (t = 0 s, =1.639 × 10−10 mol s−1), the growth rates of the unidirectional flux are 0.43 % at 2 μs, 4.03 % at 6 μs, and 5.49 % at 10 μs, respectively. The aforementioned findings indicate that ultrasonic cavitation has an important prospect in opening the BBB.
Fig. 10.
The unidirectional flux of the model at different times under ultrasonic excitation. The values in the figure represent the unidirectional flux (mol s−1).
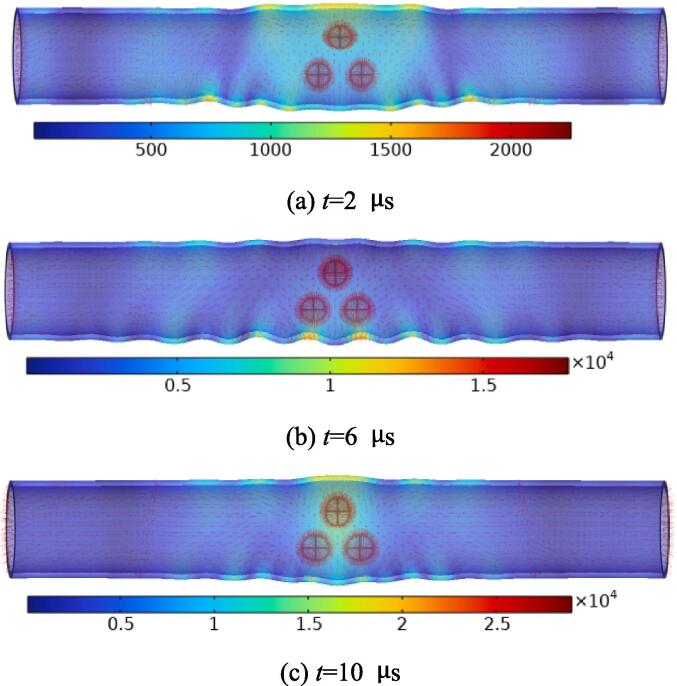
In order to further describe the stress distribution in the blood vessel wall driven by ultrasonic cavitation. Based on the small deformation assumptions, Fig. 11 depicts the bubble motion in the lumen and the stress distribution in the blood vessel wall at different times. On the one hand, the streamline density near the bubble is highest. On the other hand, the wall stress caused by bubble motion is also the largest. The maximum stress values of blood vessel wall are 2.252 × 103 N/m2 at 2 μs, 1.780 × 104 N/m2 at 6 μs, and 2.901 × 104 N/m2 at 10 μs, respectively. It is worth noting that the shape of the bubbles gradually changes from round to oval, and the bubbles in the middle seem to have a tendency to be flattened.
Fig. 11.
The stress distribution of the model at different times under ultrasonic excitation. The values in the figure represent the wall stress (N/m2).
4. Discussion
There may be various uncontrollable factors in clinical practice. A large number of studies have proved that environmental factors and ultrasonic excitation conditions have a non-negligible relationship with ultrasonic cavitation. In this section, we will analyze the effects of acoustic parameters and environmental factors on the results.
4.1. Effect of frequency
In Fig. 12(a), we calculated the maximum TD of the upper and lower vessel walls at three ultrasonic excitation frequencies. In the frequency range 0.9 MHz to 1.1 MHz, we can know that the higher the ultrasonic excitation frequency, the shorter the duration. At the 10th microsecond, the maximum TD is 0.186 m at 0.9 MHz, 0.221 m at 1.0 MHz, and 0.248 m at 1.1 MHz, respectively. In this frequency band, TD increases with frequency. To be noted, the damage that ultrasonic cavitation causes to the “bridges” that connect the substances in the target tissue is irreversible, despite the fact that the data show that the kinematic displacement of the vessel wall generated by ultrasonic cavitation appears to be reversible [83]. Therefore, it can be seen that the time of focused ultrasound should not be too long. Studies have shown that the biological effects of bubble motion are related to its initial radius [31], [38]. At the 10th microsecond, we describe the TD-bubble initial radius curve in Fig. 12(b) at different frequencies. In conclusion, it appears that the greater the initial radius value, the greater the value of TD. However, in the same scenario, the value of TD after altering the frequency does not seem to have any rules to be found. Nevertheless, as we can see in Fig. 12(c) and Fig. 12(d), there appears to be a relationship between frequency and unidirectional flux as well as shear stress. So, picking the right frequency is more crucial. In addition, under extended high-frequency focused ultrasound, it does not only increase the temperature of the target tissue leading to denaturation [84], [85], but also causes greater mechanical damage to the target tissue [13], [31], [83], which requires attention in clinical practice.
Fig. 12.
The effect of different ultrasound frequencies on model results under ultrasonic excitation.
4.2. Effect of cycle number
Fig. 13 illustrates the total displacement, shear stress and unidirectional flux at different number of cycles N in the ultrasonic burst. We can know that the smaller the N, the shorter the burst time. At the 10th microsecond, the maximum total displacement are 0.163 m at N=2, 0.114 m at N=5, and 0.068 m at N=8, respectively. In a short time, the greater the N is, the lighter the intensity of bubble motion gets. In Wang et al.’s report, they employed the analytical solution to investigate the impact of cycle number (N=3, 5, 7) on the motion of bubbles, based on the assumption of an infinite domain environment [38]. They find that the speed of bubble driven by burst wave with large N is more strong when the time is longer (t > 40 s). However, it appears that the speed of bubble driven by burst wave with tiny N is more intense for shorter simulation times [38], which is consistent with the results obtained in this paper.
Fig. 13.
The effect of different number of cycles on model results under ultrasonic excitation.
4.3. Effects of bubble–bubble distance
Insonation of bubbles at a sufficiently high concentration results in changes in the permeability of capillary wall [86]. Studies have shown that high concentrations bubbles can increase the bubble signal amplitude through the skull and improved the quality of the spectrograms at matched pressures [87]. In order to further study the effect of different contrast agent concentration or bubble concentration on blood vessel wall, we discussed the distance between bubbles. It can be seen from Fig. 14(a) that the larger the value of , the smaller the value of TD. At 10th microsecond, the maximum total displacement is 0.156 μm at 7 μm, 0.114 μm at 8 μm, and 0.093 μm at 9 μm, respectively. Nevertheless, we can see in Fig. 14(b) and (c) that the greater the distance between the bubbles, the maximum unidirectional flux and the maximum shear stress of the wall appear to be larger, this is probably due to the fact that the closer the bubbles are to the blood vessel wall, the more pressure and shear stress they cause. The results show that the concentration of ultrasound contrast agent has a great influence on the ultrasonic cavitation effect. When using ultrasound contrast agent for treatment, the concentration should be strictly controlled.
Fig. 14.
The effect of different bubble–bubble distances on model results under ultrasonic excitation.
4.4. Effect of ultrasonic amplitude
Higher ultrasonic amplitudes result in higher energy inputs into the system, which might cause more violent energy transformations and raise the possibility of bubble collapse [88]. In addition, the higher the ultrasound amplitude has, the more violent the bubble gets, and the maximum temperature inside the bubble as well as the maximum pressure increase [89]. Fig. 15 depicts the influence of different ultrasonic amplitudes on the model results, and the greater the ultrasonic amplitude, the greater the stress of the blood vessel wall. At 10th microseconds, the maximum stress values of blood vessel wall are 1.416 × 104 N/m2 at 0.02 MPa, 2.901 × 104 N/m2 at 0.04 MPa, and 4.966 × 104 N/m2 at 0.06 MPa, respectively. It is worth noting that the larger the ultrasonic amplitude, the more obvious the intermediate bubble is compressed.
Fig. 15.
The stress distribution of the model at different ultrasonic amplitudes under ultrasonic excitation. The values in the figure represent the wall stress (N/m2).
The fluctuation of the wall shear stress and maximum unidirectional flux for various ultrasonic amplitudes are shown in Fig. 16. It can be found that the larger the ultrasonic amplitude, the larger the wall shear stress as well as the maximum unidirectional flux. The results indicate that the ultrasonic amplitude has a larger effect on the wall shear stress and pressure. Prior research has demonstrated that the wall stress caused by bubble rupture can potentially exceed hundreds of GPa [90], the right ultrasonic amplitude must be carefully chosen in clinical setting because prolonged exposure to high energy levels might cause cell injury or separation when bubble bursts [31], [83].
Fig. 16.
The effect of different ultrasonic amplitudes on wall shear stress and unidirectional flux under ultrasonic excitation.
4.5. Effect of ambient radius of bubbles
In this section, we focus on the influence of the initial radius of the bubble on the results. We assume that the initial bubble radii are 1.5 μm, 2 μm and 2.5 μm, respectively. In Fig. 17, we can know that the initial bubble radium has a great influence on the wall displacement. With the increase of the initial bubble radii, the movement of the bubble seems to be gradually intense. The calculation results are consistent with the related research results [38].
Fig. 17.
The maximum total displacement at three different initial radius (R10 = R20 = R30, f = 1.0 MHz, N = 5, RL = 8 μm).
It should be noted that the above calculation is based on the assumption that the radii of the three bubbles are equal. Here we will focus on describing the case of different radius. We assume that the radii of and are both 2 μm, and the radii of are 1.5 μm, 2 μm and 2.5 μm, respectively (Fig. 18). At 10th microseconds, on the one hand, the maximum stress values in the three cases are different, the maximum stress values of blood vessel wall are 2.727 × 104 N/m2 at , 2.901 × 104 N/m2 at , and 8.085 × 104 N/m2 at , respectively, it seems that the larger the initial radius of the bubble, the higher the wall stress. On the other hand, the shapes of the bubbles are also quite different, but it seems that the large bubbles will suppress the small bubbles, which is consistent with the relevant research results [76], [77], [78].
Fig. 18.
The stress distribution of the model at different under ultrasonic excitation. The values in the figure represent the wall stress (N/m2).
The maximum unidirectional flux and maximum shear stress variation curves are shown in Fig. 19, which is based on Fig. 18. Interestingly, it seems that when the three radii are equal, the values of the maximum unidirectional flux and maximum shear stress are the smallest, To put it another way, the system as a whole is the most stable, which can be informative for clinical practice.
Fig. 19.
With the ultrasonic excitation, the stress distribution of the model at different .
In addition, when f = 1.0 MHz, N=5, RL=8 , and we calculate the case of three bubbles with different radii. It can be seen that the results of Fig. 20 are similar to those of Fig. 18. Small bubbles are inhibited from developing by larger ones, and the signs of compression on the surface of smaller bubbles appear to be more noticeable. It should be noted that the wall stress and unidirectional flux have the largest values near the largest bubbles, perhaps resulting from the closer distance from the vessel wall (not shown in the Fig. 20).
Fig. 20.T.
He stress distribution of the model at different times under ultrasonic excitation. The values in the figure represent the wall stress (N/m2).
4.6. Effect of viscosity coefficient
It has been demonstrated that lowering the liquid’s viscosity coefficient causes the bubbles to move more quickly, boosting the cavitation impact of focused ultrasound [91], [92]. More specifically, increasing medium viscosity drastically dampens the bubble dynamics and weakens the strength of bubble collapse. The cavitation dynamics of differently-sized bubbles depend differently on the medium viscoelasticity, and each bubble is affected by its neighboring bubbles to a different degree [93]. Fig. 21 calculated the radius of bubble 3, and shows the maximum values of unidirectional flux and shear stress variation for different viscosity coefficients. We can find that the smaller the coefficient of viscosity, the greater the degree of bubble motion and the maximum unidirectional flux, as well as the maximum shear stress value. Therefore, the viscosity of the patient’s blood has a certain impact on the clinical treatment of cavitation effect.
Fig. 21.
The effect of different viscosity coefficients on model results under ultrasonic excitation.
4.7. Effect of bubble arrangement
Here, we discuss the arrangement of bubbles. Based on the calculation conditions in Fig. 11, we assume that the lumen radius is 5 μm, and the three bubbles are evenly distributed on the center line of the blood vessel. In Fig. 22, we calculate the bubble radius (not shown in the figure.), secondary Bjerknes force (Fig. 22(a)), vessel displacement (Fig. 22(b)), wall shear stress (Fig. 22(c)), and the wall permeability (Fig. 22(d)) at three different moments. On the one hand, the results show that the trend of bubble dynamics is consistent with Fig. 6(a), but the numerical gap is relatively obvious. On the other hand, the displacement, shear stress and permeability at the bubble are larger than other locations (Fig. 22(b)-Fig. 22(d)). It should be noted that there is a significant gap in the secondary Bjerknes force between bubbles compared with Fig. 6(b), the secondary Bjerknes force between bubble 1 and bubble 2 is the smallest, which may be caused by the farthest distance.
Fig. 22.
The influence of bubble arrangement on the model results (Bubbles are evenly distributed in the cavity).
Finally, we further explore the influence of the arrangement of bubbles on the model results. Based on the small deformation assumptions, Fig. 23 depicts the bubble motion in the lumen and the stress distribution in the blood vessel wall at different times. It can be seen that the results are basically consistent with the conclusions of Fig. 11. The maximum stress of blood vessel wall is 6.394 × 103 N/m2 at 2 μs, 8.103 × 103 N/m2 at 6 μs, and 1.944 × 104 N/m2 at 10 μs, respectively. In addition, the maximum unidirectional flux are 1.644 × 10−10 mol s−1 at 2 μs, 1.677 × 10−10 mol s−1 at 6 μs, and 1.691 × 10−10 mol s−1at 10 μs, respectively (not shown in the figure). From the above, it is evident that the triangular configuration of the bubbles appears to have a more notable impact on the vascular wall, potentially resulting in a higher concentration of bubbles.
Fig. 23.
The stress distribution of the model at different times under ultrasonic excitation. The values in the figure represent the wall stress (N/m2).
5. Conclusion
This paper describes the dynamic behavior of the three-bubble system and its effect on the vascular walls, including wall displacement, permeability and unidirectional flux (Taking amoxicillin as an example), etc. The interaction between bubbles and the interaction between bubbles and biological tissue were considered in this model, and deeply analyzed for the influence of environmental factors and ultrasonic parameters. The findings demonstrate that the BBB can be momentarily and reversibly opened by bubble motion, increasing the permeability and mass flux of walls. The opening degree of the BBB is related to the bubble concentration, the initial radius of the bubble, the distribution of the bubbles, and the sound pressure. The findings demonstrated that the velocity of bubble motion and drug flux increased with increasing ultrasonic amplitude or reducing viscosity coefficient. The drug flux is trending upward as ultrasonic action duration increases, and the drug permeation effect is significantly influenced by the bubble radius’s size. In low viscosity liquids, the unidirectional flux growth rate of the wall can reach more than 5 % when the initial radius of the bubbles, the ultrasonic frequency and the ultrasonic amplitude are 2 μm, 1 MHz and 0.04 MPa, respectively, but when the bubbles are arranged in a straight line inside the vessel, the unidirectional flux is significantly less. On the other hand, the bubbles will also extrude one another, and the deformation rate of bubbles is related to acoustic parameters.
It should be mentioned that bubbles typically exist as bubble clusters. Furthermore, the explosion of the bubbles may generate high temperatures and pressures [94], [95]. These effects are not taken into account in this research. Some papers have taken into account the existence of a magnetic field when examining the ultrasonic cavitation impact [96], [97]. Moreover, some studies have included deep learning into their research methodology to find the best possible model [98], [99]. All of the above questions are worth exploring in the future.
In conclusion, this study demonstrates a preliminary and comprehensive understanding of the mechanism by which ultrasonic cavitation opens the blood–brain barrier. Our model on ultrasonic cavitation within microvessels may provide a new choice for the treatment of brain diseases.
CRediT authorship contribution statement
Weirui Lei: Writing – review & editing, Writing – original draft, Supervision, Project administration, Investigation. Shuai Chang: Supervision, Project administration, Investigation. Feng Tian: Supervision, Project administration, Investigation. Xiao Zou: Supervision, Project administration, Investigation. Jiwen Hu: Writing – review & editing, Writing – original draft, Supervision, Funding acquisition. Shengyou Qian: Writing – review & editing, Writing – original draft, Project administration, Funding acquisition.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This study was supported by the National Nature Science Foundation of China (No. 12274200, 11774088), the Scientific Research Foundation of Education Department of Hunan Province of China (No. 22B0036), Changsha Municipal Natural Science Foundation of China (No. kq2202239) and Hengyang Science and Technology Plan Projects (No. 202250045335).
Contributor Information
Xiao Zou, Email: shawner@hunnu.edu.cn.
Jiwen Hu, Email: hu_sanping@163.com.
Shengyou Qian, Email: shyqian@hunnu.edu.cn.
Data availability
All data generated or used during the study appear in the submitted article.
References
- 1.Ye L., Zhu X., Liu Y. Numerical study on dual-frequency ultrasonic enhancing cavitation effect based on bubble dynamic evolution. Ultrason. Sonochem. 2019;59 doi: 10.1016/j.ultsonch.2019.104744. [DOI] [PubMed] [Google Scholar]
- 2.Margulis M.A. Sonoluminescence and sonochemical reactions in cavitation fields. A review. Ultrasonics. 1985;23(4):157–169. doi: 10.1016/0041-624X(85)90024-1. [DOI] [Google Scholar]
- 3.Hu J., Lu X., Liu Y., et al. Numerical and experimental investigations on the jet and shock wave dynamics during the cavitation bubble collapsing near spherical particles based on OpenFOAM. Ultrason. Sonochem. 2023;99 doi: 10.1016/j.ultsonch.2023.106576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Liu W., Li N., Weng C., et al. Bubble dynamics and pressure field characteristics of underwater detonation gas jet generated by a detonation tube. Phys. Fluids. 2021;33(2) doi: 10.1063/5.0029729. [DOI] [Google Scholar]
- 5.Favvas E.P., Kyzas G.Z., Efthimiadou E.K., et al. Bulk nanobubbles, generation methods and potential applications. Curr. Opin. Colloid. Interface Sci. 2021;54 doi: 10.1016/j.cocis.2021.101455. [DOI] [Google Scholar]
- 6.Gurung A., Dahl O., Jansson K. The fundamental phenomena of nanobubbles and their behavior in wastewater treatment technologies. Geosystem. Eng. 2016;19(3):133–142. doi: 10.1080/12269328.2016.1153987. [DOI] [Google Scholar]
- 7.Mapukata S., Ntsendwana B., Mokhena T., et al. Advances on sonophotocatalysis as a water and wastewater treatment technique: efficiency, challenges and process optimisation. Front. Chem. 2023;11:1252191. doi: 10.3389/fchem.2023.1252191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gadipelly C., Pérez-González A., Yadav G.D., et al. Pharmaceutical industry wastewater: review of the technologies for water treatment and reuse. Ind. Eng. Chem. Res. 2014;53(29):11571–11592. doi: 10.1021/ie501210j. [DOI] [Google Scholar]
- 9.Shi X., Tal G., Hankins N.P., et al. Fouling and cleaning of ultrafiltration membranes: a review. J. Water. Process. Eng. 2014;1:121–138. doi: 10.1016/j.jwpe.2014.04.003. [DOI] [Google Scholar]
- 10.Batouti M.E., Alharby N.F., Elewa M.M. Review of new approaches for fouling mitigation in membrane separation processes in water treatment applications. Separations. 2021;9(1):1. doi: 10.3390/separations9010001. [DOI] [Google Scholar]
- 11.Krasovitski B., Frenkel V., Shoham S., et al. Intramembrane cavitation as a unifying mechanism for ultrasound-induced bioeffects. Proc. Natl. Acad. Sci. India B. 2011;108(8):3258–3263. doi: 10.1073/pnas.1015771108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Movahed P., Kreider W., Maxwell A.D., et al. Cavitation-induced damage of soft materials by focused ultrasound bursts: a fracture-based bubble dynamics model. J. Acoust. Soc. Am. 2016;140(2):1374–1386. doi: 10.1121/1.4961364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu W., Hu J., Liu Y., et al. Numerical analysis of the biomechanical effects on micro-vessels by ultrasound-driven cavitation. Acta. Bioeng. Biomech. 2021;23(1) doi: 10.37190/ABB-01749-2020-03. [DOI] [PubMed] [Google Scholar]
- 14.Karthikesh M.S., Yang X. The effect of ultrasound cavitation on endothelial cells. Exp. Biol. Med. 2021;246(7):758–770. doi: 10.1177/1535370220982301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Adhikari U., Goliaei A., Berkowitz M.L. Nanobubbles, cavitation, shock waves and traumatic brain injury. Phys. Chem. Chem. Phys. 2016;18(48):32638–32652. doi: 10.1039/C6CP06704B. [DOI] [PubMed] [Google Scholar]
- 16.Lei W., Hu J., Liu Y., et al. Numerical evaluation of high-intensity focused ultrasound-induced thermal lesions in atherosclerotic plaques. Math. Biosci. Eng. 2021;18:1154–1168. doi: 10.3934/mbe.2021062. [DOI] [PubMed] [Google Scholar]
- 17.Brahmandam A., Chan S.M., Dardik A., et al. A narrative review on the application of high-intensity focused ultrasound for the treatment of occlusive and thrombotic arterial disease. JVS-Vascular Sci. 2022;3:292–305. doi: 10.1016/j.jvssci.2022.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Meng Y., Pople C.B., Lea-Banks H., et al. Safety and efficacy of focused ultrasound induced blood-brain barrier opening, an integrative review of animal and human studies. J. Control. Release. 2019;309:25–36. doi: 10.1016/j.jconrel.2019.07.023. [DOI] [PubMed] [Google Scholar]
- 19.Burgess A., Shah K., Hough O., et al. Focused ultrasound-mediated drug delivery through the blood–brain barrier. Expert Rev. Neurotherapeutics. 2015;15(5):477–491. doi: 10.1586/14737175.2015.1028369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fan C.H., Liu H.L., Ting C.Y., et al. Submicron-bubble-enhanced focused ultrasound for blood–brain barrier disruption and improved CNS drug delivery. PLoS One. 2014;9(5):e96327. doi: 10.1371/journal.pone.0096327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Singh A., Kusunose J., Phipps M.A., et al. Guiding and monitoring focused ultrasound mediated blood–brain barrier opening in rats using power Doppler imaging and passive acoustic map**. Sci. Rep.-UK. 2022;12(1):14758. doi: 10.1038/s41598-022-18328-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Burgess A., Nhan T., Moffatt C., et al. Analysis of focused ultrasound-induced blood–brain barrier permeability in a mouse model of Alzheimer’s disease using two-photon microscopy. J. Control. Release. 2014;192:243–248. doi: 10.1016/j.jconrel.2014.07.051. [DOI] [PubMed] [Google Scholar]
- 23.Choi J.J., Feshitan J.A., Baseri B., et al. Microbubble-size dependence of focused ultrasound-induced blood–brain barrier opening in mice in vivo. IEEE T. Bio-Med. Eng. 2009;57(1):145–154. doi: 10.1109/TBME.2009.2034533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Poon C., Mühlenpfordt M., Olsman M., et al. Real-time intravital multiphoton microscopy to visualize focused ultrasound and microbubble treatments to increase blood-brain barrier permeability. JoVE-J. vis. Exp. 2022;180:e62235. doi: 10.3791/62235. [DOI] [PubMed] [Google Scholar]
- 25.McMahon D., Hynynen K. Acute inflammatory response following increased blood-brain barrier permeability induced by focused ultrasound is dependent on microbubble dose. Theranostics. 2017;7(16):3989. doi: 10.7150/thno.21630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yan Y., Chen Y., Liu Z., et al. Brain delivery of curcumin through low-intensity ultrasound-induced blood–brain barrier opening via lipid-plga nanobubbles. Int. J. Nanomed. 2021;16:7433–7447. doi: 10.2147/IJN.S327737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Felix M.S., Borloz E., Metwally K., et al. Ultrasound-mediated blood-brain barrier opening improves whole brain gene delivery in mice. Pharmaceutics. 2021;13(8):1245. doi: 10.3390/pharmaceutics13081245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ting C.Y., Fan C.H., Liu H.L., et al. Concurrent blood–brain barrier opening and local drug delivery using drug-carrying microbubbles and focused ultrasound for brain glioma treatment. Biomaterials. 2012;33(2):704–712. doi: 10.1016/j.biomaterials.2011.09.096. [DOI] [PubMed] [Google Scholar]
- 29.Deng C.X. Targeted drug delivery across the blood–brain barrier using ultrasound technique. Ther. Deliv. 2010;1(6):819–848. doi: 10.4155/tde.10.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hosseinkhah N., Goertz D.E., Hynynen K. Microbubbles and blood–brain barrier opening: a numerical study on acoustic emissions and wall stress predictions. IEEE. T. Bio-Med. Eng. 2014;62(5):1293–1304. doi: 10.1109/TBME.2014.2385651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Xie Y., Hu J., Lei W., et al. Prediction of vascular injury by cavitation microbubbles in a focused ultrasound field. Ultrason. Sonochem. 2022;88 doi: 10.1016/j.ultsonch.2022.106103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hosseinkhah N., Hynynen K. A three-dimensional model of an ultrasound contrast agent gas bubble and its mechanical effects on microvessels. Phys. Med. Biol. 2012;57(3):785. doi: 10.1088/0031-9155/57/3/785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wiedemair W., Tuković Ž., Jasak H., et al. On ultrasound-induced microbubble oscillation in a capillary blood vessel and its implications for the blood–brain barrier. Phys. Med. Biol. 2012;57(4):1019. doi: 10.1088/0031-9155/57/4/1019. [DOI] [PubMed] [Google Scholar]
- 34.Miao H., Gracewski S.M., Dalecki D. Ultrasonic excitation of a bubble inside a deformable tube: implications for ultrasonically induced hemorrhage. J. Acoust. Soc. Am. 2008;124(4):2374–2384. doi: 10.1121/1.2967488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen C., Gu Y., Tu J., et al. Microbubble oscillating in a microvessel filled with viscous fluid: a finite element modeling study. Ultrasonics. 2016;66:54–64. doi: 10.1016/j.ultras.2015.11.010. [DOI] [PubMed] [Google Scholar]
- 36.Mirsandi H., Kong G., Buist K.A., et al. Numerical study on the interaction of two bubbles rising side-by-side in viscous liquids. Chem. Eng. J. 2021;410 doi: 10.1016/j.cej.2020.128257. [DOI] [Google Scholar]
- 37.Agrawal M., Gaurav A., Karri B., et al. An experimental study of two identical air bubbles rising side-by-side in water. Phys. Fluids. 2021;33 doi: 10.1063/5.0044485. [DOI] [Google Scholar]
- 38.Wang X., Chen W., Zhou M., et al. Dynamics of double bubbles under the driving of burst ultrasound. Ultrason. Sonochem. 2022;84 doi: 10.1016/j.ultsonch.2022.105952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liang J.F., Liu J.X. Dynamics of three cavitation bubbles with pulsation and symmetric deformation. Ultrason. Sonochem. 2023;96 doi: 10.1016/j.ultsonch.2023.106428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wu Y., Chen W., Zhang L., et al. The left-right symmetrical and asymmetrical deformations in a three-bubble system. J. Acoust. Soc. Am. 2022;152(4):2446–2455. doi: 10.1121/10.0014905. [DOI] [PubMed] [Google Scholar]
- 41.Lei W., Qian S., Zhu X., et al. Haemodynamic effects on the development and stability of atherosclerotic plaques in arterial blood vessel. Interdiscip. Sci. 2023;15(4):616–632. doi: 10.1007/s12539-023-00576-w. [DOI] [PubMed] [Google Scholar]
- 42.White M.C., Godfrey M.M. Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 2008;40(1):235–256. doi: 10.1146/annurev.fluid.40.111406.102156. [DOI] [Google Scholar]
- 43.Lei W., Hu J., Xie Y., et al. Mathematical modelling of the effects of statins on the growth of necrotic core in atherosclerotic plaque. Math. Model. Nat. Pheno. 2023;18:11. doi: 10.1051/mmnp/2023005. [DOI] [Google Scholar]
- 44.Cilla M., Pena E., Martinez M.A. Mathematical modelling of atheroma plaque formation and development in coronary arteries. J. R. Soc. Interface. 2014;11(90):20130866. doi: 10.1098/rsif.2013.0866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cheng Z., Zhang W., Ning Z., et al. Wettability control on imbibition behavior of oil and water in porous media. Phys. Fluids. 2022;34(7) doi: 10.1063/5.0100051. [DOI] [Google Scholar]
- 46.Hariharan P., Nabili M., Guan A., et al. Model for porosity changes occurring during ultrasound-enhanced transcorneal drug delivery. Ultrasound. Med. Biol. 2017;43(6):1223–1236. doi: 10.1016/j.ultrasmedbio.2017.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li D.F., Li C.F., Shu S.Q., et al. A fast and accurate analysis of the interacting cracks in linear elastic solids. Int. J. Fracture. 2008;151:169–185. doi: 10.1007/s10704-008-9249-8. [DOI] [Google Scholar]
- 48.Qin S., Ferrara K.W. Acoustic response of compliable microvessels containing ultrasound contrast agents. Phys. Med. Biol. 2006;51(20):5065–5088. doi: 10.1088/0031-9155/51/20/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Qin D., Zou Q., Lei S., et al. Cavitation dynamics and inertial cavitation threshold of lipid coated microbubbles in viscoelastic media with bubble–bubble interactions. Micromachines-Basel. 2021;12(9):1125. doi: 10.3390/mi12091125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang Y., Cai J., Li Q. Numerical simulation of large bubble-rising behavior in nuclear reactor using diffuse interface method. Int. J. Energ. Res. 2018;42(1):276–283. doi: 10.1002/er.3942. [DOI] [Google Scholar]
- 51.Zhang Y., Li S. The secondary Bjerknes force between two gas bubbles under dual-frequency acoustic excitation. Ultrason. Sonochem. 2016;29:129–145. doi: 10.1016/j.ultsonch.2015.08.022. [DOI] [PubMed] [Google Scholar]
- 52.Yang H., Sun Y., Wei J., et al. The effects of ultrasound-targeted microbubble destruction (UTMD) carrying IL-8 monoclonal antibody on the inflammatory responses and stability of atherosclerotic plaques. Biomed. Pharmacother. 2019;118 doi: 10.1016/j.biopha.2019.109161. [DOI] [PubMed] [Google Scholar]
- 53.Lin S.J., Jan K.M., Weinbaum S., et al. Transendothelial transport of low density lipoprotein in association with cell mitosis in rat aorta. Arteriosclerosis. 1989;9(2):230–236. doi: 10.1161/01.ATV.9.2.230. [DOI] [PubMed] [Google Scholar]
- 54.Olgac U., Kurtcuoglu V., Poulikakos D. Computational modeling of coupled blood-wall mass transport of LDL: effects of local wall shear stress. Am. J. Physiol-Heart. C. 2008;294(2):H909–H919. doi: 10.1152/ajpheart.01082.2007. [DOI] [PubMed] [Google Scholar]
- 55.Robinson P.J., Rapoport S.I. Size selectivity of blood-brain barrier permeability at various times after osmotic opening. Am. J. Physiol-Reg. I. 1987;253(3):R459–R466. doi: 10.1152/ajpregu.1987.253.3.R459. [DOI] [PubMed] [Google Scholar]
- 56.Liu Y. Mathematical modeling and simulation of atherosclerotic formation and progress at arterial bifurcations. Biomed. Signal. Process. 2023;80 doi: 10.1016/j.bspc.2022.104266. [DOI] [Google Scholar]
- 57.Lénárt N., Walter F.R., Bocsik A., et al. Cultured cells of the blood–brain barrier from apolipoprotein B-100 transgenic mice: effects of oxidized low-density lipoprotein treatment. Fluids. Barriers. CNS. 2015;12:1–16. doi: 10.1186/s12987-015-0013-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Renkin E.M. Filtration, diffusion, and molecular sieving through porous cellulose membranes. Physiology. 1954;38(2):225–243. doi: 10.1085/jgp.38.2.225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Carey S.K., Quinton W.L., Goeller N.T. Field and laboratory estimates of pore size properties and hydraulic characteristics for subarctic organic soils. Processes. 2007;21(19):2560–2571. doi: 10.1002/hyp.6795. [DOI] [Google Scholar]
- 60.Fu Y., Bian X., Zou R., et al. Hemodynamic alterations of flow diverters on aneurysms at the fetal posterior communicating artery: a simulation study using CFD to compare the surpass streamline, pipeline flex, and tubridge devices. J. Neuroradiol. 2024;51(1):74–81. doi: 10.1016/j.neurad.2023.07.002. [DOI] [PubMed] [Google Scholar]
- 61.Innocenti A., Fox R.O., Salvetti M.V., et al. A Lagrangian probability-density-function model for collisional turbulent fluid–particle flows. J. Fluid Mech. 2019;862:449–489. doi: 10.1017/jfm.2018.895. [DOI] [Google Scholar]
- 62.Mofakham A.A., Ahmadi G. Improved discrete random walk stochastic model for simulating particle dispersion and deposition in inhomogeneous turbulent flows. J. Fluid. Eng.-T. ASME. 2020;142(10) doi: 10.1115/1.4047538. [DOI] [Google Scholar]
- 63.Klotz A.R., Hynynen K. Simulations of the Devin and Zudin modified Rayleigh-Plesset equations to model bubble dynamics in a tube. Technical. Acoustics. 2010;17:11–26. http://www.ejta.org, 2010, 11. [Google Scholar]
- 64.Aganin A.A., Kosolapova L.A., Malakhov V.G. Bubble dynamics near a locally curved region of a plane rigid wall. Phys. Fluids. 2022;34(9) doi: 10.1063/5.0105955. [DOI] [Google Scholar]
- 65.Tomita Y., Robinson P.B., Tong R.P., et al. Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid. Mech. 2002;466:259–283. doi: 10.1017/S0022112002001209. [DOI] [Google Scholar]
- 66.Akyildiz A.C., Speelman L., Brummelen H.V., et al. Effects of intima stiffness and plaque morphology on peak cap stress. Biomed. Eng. Online. 2011;10:1–13. doi: 10.1186/1475-925X-10-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Xie J., Zhou J., Fung Y.C. Bending of blood vessel wall: stress-strain laws of the intima-media and adventitial layers. J. Biomech. Sci. Eng. 1995;1(136):136–145. doi: 10.1115/1.2792261. [DOI] [PubMed] [Google Scholar]
- 68.Khanafer K., Berguer R. Fluid–structure interaction analysis of turbulent pulsatile flow within a layered aortic wall as related to aortic dissection. J. Biomech. 2009;42(16):2642–2648. doi: 10.1016/j.jbiomech.2009.08.010. [DOI] [PubMed] [Google Scholar]
- 69.Ri J., Pang N., Bai S., et al. Three-dimensional numerical analysis of wall stress induced by asymmetric oscillation of microbubble trains inside micro-vessels. Phys. Fluids. 2023;35(1) doi: 10.1063/5.0134922. [DOI] [Google Scholar]
- 70.Garbin V., Dollet B., Overvelde M., et al. History force on coated microbubbles propelled by ultrasound. Phys. Fluids. 2009;21(9) doi: 10.1063/1.3227903. [DOI] [Google Scholar]
- 71.Abbott N.J., Patabendige A.A.K., Dolman D.E.M., et al. Structure and function of the blood–brain barrier. Neurobiol. Dis. 2010;37(1):13–25. doi: 10.1016/j.nbd.2009.07.030. [DOI] [PubMed] [Google Scholar]
- 72.Obermeier B., Daneman R., Ransohoff R.M. Development, maintenance and disruption of the blood-brain barrier. Nat. Med. 2013;19(12):1584–1596. doi: 10.1038/nm.3407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Pardridge W.M. Drug transport across the blood–brain barrier. J. Cerebr. Blood. F. Met. 2012;32(11):1959–1972. doi: 10.1038/jcbfm.2012.126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sheikov N., McDannold N., Vykhodtseva N., et al. Cellular mechanisms of the blood-brain barrier opening induced by ultrasound in presence of microbubbles. Ultrasound. Med. Biol. 2004;30(7):979–989. doi: 10.1016/j.ultrasmedbio.2004.04.010. [DOI] [PubMed] [Google Scholar]
- 75.Deprez J., Lajoinie G., Engelen Y., et al. Opening doors with ultrasound and microbubbles: beating biological barriers to promote drug delivery. Adv. Drug. Deliver. Rev. 2021;172:9–36. doi: 10.1016/j.addr.2021.02.015. [DOI] [PubMed] [Google Scholar]
- 76.Mesiwala A.H., Farrell L., Wenzel H.J., et al. High-intensity focused ultrasound selectively disrupts the blood-brain barrier in vivo. Ultrasound. Med. Biol. 2002;28(3):389–400. doi: 10.1016/s0301-5629(01)00521-x. [DOI] [PubMed] [Google Scholar]
- 77.Sun Y., Du Y., Yao Z., et al. The effect of surface geometry of solid wall on the collapse of a cavitation bubble. J. Fluid. Eng.-T. ASME. 2022;144(7) doi: 10.1115/1.4053350. [DOI] [Google Scholar]
- 78.You Q., Shao X., Wang J., et al. Progress on physical field-regulated micro/nanomotors for cardiovascular and cerebrovascular disease treatment. Small. Methods. 2023;7(10):2300426. doi: 10.1002/smtd.202300426. [DOI] [PubMed] [Google Scholar]
- 79.Pitt W.G., Husseini G.A., Staples B.J. Ultrasonic drug delivery–a general review. Expert. Opin. Drug. Delivery. 2004;1(1):37–56. doi: 10.1517/17425247.1.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.VanBavel E. Effects of shear stress on endothelial cells: possible relevance for ultrasound applications. Prog. Biophys. Mol. Bio. 2007;93(1–3):374–383. doi: 10.1016/j.pbiomolbio.2006.07.017. [DOI] [PubMed] [Google Scholar]
- 81.Yu H., Chen S. A model to calculate microstreaming-shear stress generated by oscillating microbubbles on the cell membrane in sonoporation. Bio-Med. Mater. Eng. 2014;24(1):861–868. doi: 10.3233/BME-130878. [DOI] [PubMed] [Google Scholar]
- 82.Vos H.J., Dollet B., Versluis M., et al. Nonspherical shape oscillations of coated microbubbles in contact with a wall. Ultrasound. Med. Biol. 2011;37(6):935–948. doi: 10.1016/j.ultrasmedbio.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 83.Lei W., Li A., Zhou K., et al. Study on the ultrasonic cavitation damage to early atherosclerotic plaque. Phys. Fluids. 2024;36(5) doi: 10.1063/5.0207678. [DOI] [Google Scholar]
- 84.Yang D., Ni Z., Yang Y., et al. The enhanced HIFU-induced thermal effect via magnetic ultrasound contrast agent microbubbles. Ultrason. Sonochem. 2018;49:111–117. doi: 10.1016/j.ultsonch.2018.07.031. [DOI] [PubMed] [Google Scholar]
- 85.Zawada T., Bove T. Strongly focused HIFU transducers with simultaneous optical observation for treatment of skin at 20 MHz. Ultrasound. Med. Biol. 2022;48(7):1309–1327. doi: 10.1016/j.ultrasmedbio.2022.03.002. [DOI] [PubMed] [Google Scholar]
- 86.Ferrara K.W. Driving delivery vehicles with ultrasound. Adv. Drug. Deliver. Rev. 2008;60(10):1097–1102. doi: 10.1016/j.addr.2008.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Manuel T.J., Sigona M.K., Phipps M.A., et al. Small volume blood-brain barrier opening in macaques with a 1 MHz ultrasound phased array. J. Control. Release. 2023;363:707–720. doi: 10.1016/j.jconrel.2023.10.015. [DOI] [PubMed] [Google Scholar]
- 88.Kanthale P., Ashokkumar M., Grieser F. Sonoluminescence, sonochemistry (H2O2 yield) and bubble dynamics: frequency and power effects. Ultrason. Sonochem. 2008;15(2):143–150. doi: 10.1016/j.ultsonch.2007.03.003. [DOI] [PubMed] [Google Scholar]
- 89.Wang B., Zeng T., Shang J., et al. Bubble dynamics model and its revelation of ultrasonic cavitation behavior in advanced oxidation processes: a review. J. Water. Process. Eng. 2024;63 doi: 10.1016/j.jwpe.2024.105470. [DOI] [Google Scholar]
- 90.Dular M., Petkovšek M. On the mechanisms of cavitation erosion–Coupling high speed videos to damage patterns. Exp. Therm. Fluid. Sci. 2015;68:359–370. doi: 10.1016/j.expthermflusci.2015.06.001. [DOI] [Google Scholar]
- 91.Qin D., Lei S., Chen B., et al. Numerical investigation on acoustic cavitation characteristics of an air-vapor bubble: effect of equation of state for interior gases. Ultrason. Sonochem. 2023;97 doi: 10.1016/j.ultsonch.2023.106456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Sabzeghabae A.N., Devia-Cruz L.F., Gutierrez-Herrera E., et al. Bubble dynamics of laser-induced cavitation in plasmonic gold nanorod solutions and the relative effect of surface tension and viscosity. Opt. Laser. Technol. 2021;134 doi: 10.1016/j.optlastec.2020.106621. [DOI] [Google Scholar]
- 93.Qin D., Zou Q., Zhong X., et al. Effects of medium viscoelasticity on bubble collapse strength of interacting polydisperse bubbles. Ultrason. Sonochem. 2023;95 doi: 10.1016/j.ultsonch.2023.106375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Klotz A.R., Lindvere L., Stefanovic B., et al. Temperature change near microbubbles within a capillary network during focused ultrasound. Phys. Med. Biol. 2010;55(6):1549. doi: 10.1143/JJAP.51.07GF27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Moriyama T., Yoshizawa S., Umemura S. Thermal simulation of cavitation-enhanced ultrasonic heating verified with tissue-mimicking gel. Jap. J. Appl. Phys. 2012;51(7S):07GF27. doi: 10.1143/JJAP.51.07GF27. [DOI] [Google Scholar]
- 96.Huang J., Yang J., Li L., et al. The aggregation of micro-particles based on hydraulic vortices. Phys. Fluids. 2024;36(3):032005. doi: 10.1063/5.0192288. [DOI] [Google Scholar]
- 97.Chen J., Wang C., Mo R. Dynamics of magnetic microbubble transport in blood vessels. Chinese. Phys. B. 2023;32(9) doi: 10.1088/1674-1056/aca14b. [DOI] [Google Scholar]
- 98.Li G., Sun H., He J., et al. Deep learning, numerical, and experimental methods to reveal hydrodynamics performance and cavitation development in centrifugal pump. Expert. Syst. Appl. 2024;237 doi: 10.1016/j.eswa.2023.121604. [DOI] [Google Scholar]
- 99.Choi Y., Hong S., Song J. Composite propeller design optimization for cavitation minimization using deep learning-based objective parameter prediction model. Ocean. Eng. 2023;287 doi: 10.1016/j.oceaneng.2023.115760. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or used during the study appear in the submitted article.