Toward Efficient and Unified Treatment of Static and Dynamic Correlations in Generalized Kohn–Sham Density Functional Theory

Abstract

Accurate description of the static correlation poses a persistent challenge in electronic structure theory, particularly when it has to be concurrently considered with the dynamic correlation. We develop here a method in the generalized Kohn–Sham density functional theory (DFT) framework, named R-xDH7-SCC15, which achieves an unprecedented accuracy in capturing the static correlation, while maintaining a good description of the dynamic correlation on par with the state-of-the-art DFT and wave function theory methods, all grounded in the same single-reference black-box methodology. Central to R-xDH7-SCC15 is a general-purpose static correlation correction (SCC) model applied to the renormalized XYG3-type doubly hybrid method (R-xDH7). The SCC model development involves a hybrid machine learning strategy that integrates symbolic regression with nonlinear parameter optimization, aiming to achieve a balance between generalization capability, numerical accuracy, and interpretability. Extensive benchmark studies confirm the robustness and broad applicability of R-xDH7-SCC15 across a diverse array of main-group chemical scenarios. Notably, it displays exceptional aptitude in accurately characterizing intricate reaction kinetics and dynamic processes in regions distant from equilibrium, where the influence of static correlation is most profound. Its capability to consistently and efficiently predict the whole energy profiles, activation barriers, and reaction pathways within a user-friendly “black-box” framework represents an important advance in the field of electronic structure theory.

Kohn–Sham density functional theory (KS-DFT), grounded in single-reference black-box methodology, has emerged as the preeminent electronic-structure framework for analyzing large-scale systems across diverse scientific fields.¹⁻⁶ In KS-DFT, density functional approximations (DFAs) form a development hierarchy, known as the Jacob’s Ladder, stratified into five rungs reflecting increasing complexity toward chemical accuracy.⁷ Doubly hybrid (DH) approximations, which stand on the top rung (the fifth rung) of the Jacob’s Ladder, have demonstrated significant superiority over their popular lower-rung counterparts, particularly for properties dominated by the dynamic correlation.⁸⁻²⁴ Despite this significant progress, accurately capturing the static correlation remains an unsolved challenge in KS-DFT,^4,25,26 necessitating computationally demanding multideterminant wave function treatments that are nontrivial for routine applications.^1,27

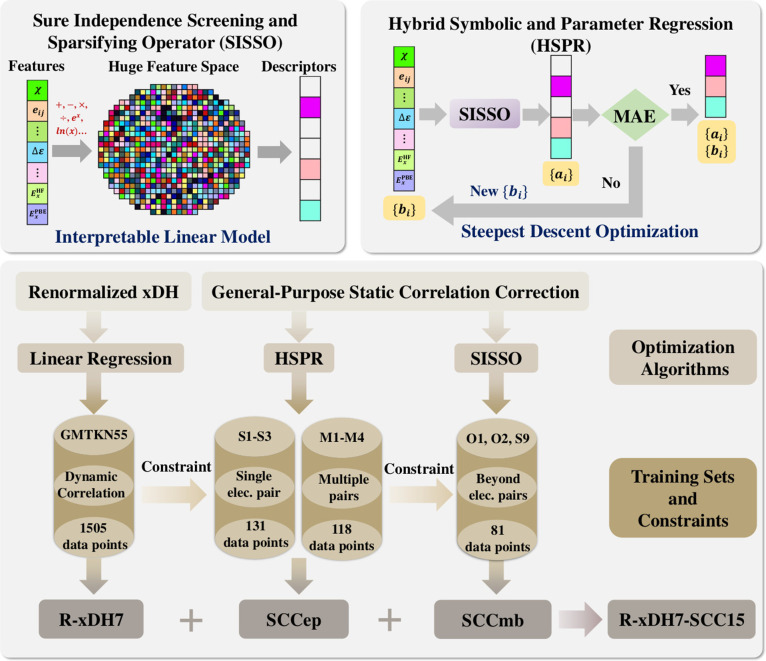
In this study, we start with the development of a renormalized XYG3-type doubly hybrid method, designated as R-xDH7, which utilizes B3LYP density and orbitals, and incorporates seven empirical parameters through an integration of a spin-distinctive random-phase approximation (RPA)-type renormalization of the second-order perturbative contribution (PT2).⁵ The R-xDH7 method encapsulates a substantial portion of the static correlation alongside a broad range of the dynamic correlation toward chemical accuracy. Based on this foundation, we further devise a general-purpose term for the residual static correlation correction specially adapted to R-xDH7 with 15 parameters (SCC15), utilizing a hybrid machine learning algorithm that synergistically combines symbolic and nonlinear parameter regressions. The working scheme is illustrated in Figure 1 and implemented in the Rust-based Electronic Structure Toolkit (REST).²⁸ The final R-xDH7-SCC15 method achieves an unprecedented balance between accuracy in describing both dynamic and static correlations. Its robustness is further underscored by the outstanding performance across a comprehensive benchmark suite for main-group chemistry, displaying its exceptional aptitude in providing precise characterizations of complex reaction mechanisms beyond the equilibrium regions where static correlation effects are significant.

Figure 1.

Development strategy for the renormalized XYG3-type doubly hybrid approximation (R-xDH7) and the machine learned static correlation correction (SCC15). Only a subset of 10 out of total 23 bond dissociation curves within the MBD23–594 (refer to Figure 2 for more details) were incorporated into the training set or utilized as constraints during the establishment of the SCC15 model.

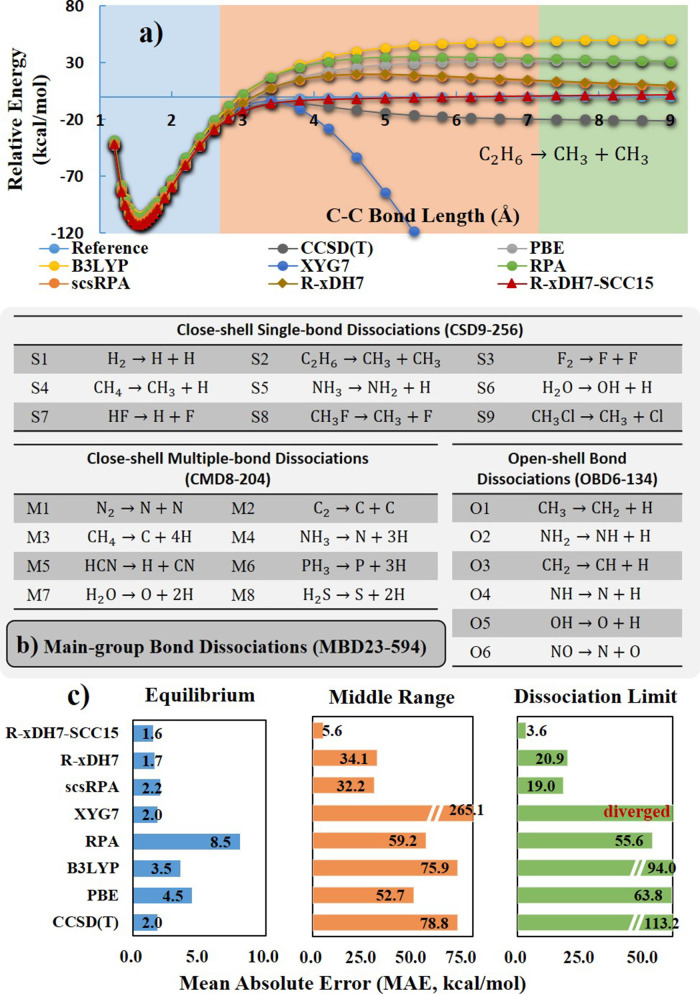
The XYG3-type doubly hybrid approximations (xDH)^12,17,24,29 have garnered widespread recognition for their ability of accurately and efficiently describing dynamic correlation effects.³⁰⁻³⁵ This is exemplified by XYG7³⁶ recently developed by our group. Some other successful examples that follow the same construction strategy as xDH are ωB97M(2)²² and xrevDSD-PBEB86-D4,³⁷ independently developed by the Head-Gordon and Martin research groups, respectively. The use of the PT2 term is a key that accounts for the notably good performance of all doubly hybrid functionals.^23,29 Despite this advancement, PT2 is notoriously inadequate for (near)-degenerated systems, where static correlation effects are predominant.⁴ As shown in Figure 2, the XYG7 results diverge during molecular bond dissociation processes. To address this shortcoming, we have previously explored enhancements to the PT2 correlation model, which included the integration of the screened second-order Bethe-Goldstone equation (sBGE2)⁶ and a spin-distinctive random-phase approximation (RPA)-type renormalization of PT2.⁵ These novel correlation models have demonstrated their efficacy in resolving the inherent divergence of PT2 in (near)-degenerated systems.⁴

Figure 2.

Assessment of various methods on the MBD23–594 data set for chemical bond dissociation. (a) Detailed depiction of calculated potential energy curves during C–C bond cleavage in ethane (C₂H₆), exemplifying method’s performance. (b) 23 bond dissociation reactions encompassed within MBD23–594, which are categorized into three subsets based on the type of bond being broken. (c) Comprehensive comparison of Mean Absolute Errors (MAEs) of these methods across three critical regions: equilibrium, middle, and the dissociation limit. All calculations were performed employing the def2-QZVPP basis set. For benchmarking, reference data were prepared using the CCSD(T) method extrapolated to the complete basis set limit (CBS) for the equilibrium region and the NVEPT2 method for the middle and dissociation limit regions.

Building upon these advancements, we introduced here a renormalized xDH method, R-xDH7, which, akin to the standard xDH method of XYG7, utilized the B3LYP³⁸⁻⁴¹ density and orbitals, but improved the standard PT2 by the spin-distinctive RPA-type renormalization⁵:

1

Here E^HF_x is the contribution from the Hartree–Fock (HF)-like exact exchange, while E^S_x and E^B88_x denote the exchange contributions from the Slater-type local density approximation (LDA)⁴² and the Becke88 generalized gradient approximation (GGA),³⁸ respectively. E^VWN_c is the local Vosko-Wilk-Nusair correlation.⁴³ The R-xDH7 method adhered to the specific VWN-III version utilized in the original B3LYP implementation to maintain consistency.⁴¹E^LYP_c is the Lee–Yang–Parr correlation approximation.³⁹ Specifically, E^osRPT2_c stands for the RPA-type renormalization of opposite-spin PT2, derived from the spin-pair distinctive adiabatic connection fluctuation–dissipation (ACFD) framework,^5,44,45 while E^ssRPT2+_c presents the difference between the standard RPA and osRPT2, which includes not only the renormalization of the same-spin PT2 but also accounts for the high-order contribution beyond PT2.⁵ Note that E^ssRPT2+_c covers only the high-order direct diagrams within the same-spin channel, explicitly excluding the second-order screened exchange (SOSEX) contributions.⁴⁶ The seven parameters in R-xDH7 were optimized against the weighted total mean absolute deviation (WTMAD2) of 1505 relative energies of main-group chemistry in the GMTKN55 data set,⁴⁷ which can be found in the Supporting Information (SI). While no constraints were applied to the seven parameters during the optimization process, an interesting pattern emerges in their final values. Specifically, the first parameter, associated with the HF-like exact exchange, was found to be nearly 1, suggesting that the R-xDH7 functional has less self-interaction error (SIE) than the conventional DFAs. Furthermore, the sum of the three exchange parameters (a₁, a₂, and a₃) is approximately close to 1. Likewise, the sum of the four correlation parameters is also nearly equal to 1. We believe that this balance in the final optimized values is crucial for maintaining the accuracy and stability of the functional, as it ensures that the exchange and correlation contributions are neither overemphasized nor underrepresented.

Table 1 presents the performance of various DFAs on the GMTKN55 benchmark set. Notably, the leading performers predominantly emerge from the standard PT2-based xDH methods, including ωB97M(2)²² and xrevDSD-PBEB86-D4³⁷ with an impressively small WTMAD2 of 2.19 and 2.23 kcal/mol, respectively. These methods also benefit from the pairwise dispersion corrections involving several tens of empirical parameters to properly capture nonbonded interactions. Interestingly, the XYG7 method, featuring only 7 empirical parameters, achieves an outstanding WTMAD2 of 2.05 kcal/mol, although no pairwise dispersion corrections have been adopted.³⁶ These PT2-based xDH methods outperform the best hybrid methods such as ωB97X-V⁴⁸ (3.92 kcal/mol), CF22-D⁴⁹ (3.62 kcal/mol), and also the machine-learning local hybrid DM21⁵⁰ (3.97 kcal/mol), by approximately 1.5 to 2.0 kcal/mol.

Table 1. WTMAD2 Values of Different DFAs (in kcal/mol) for the Full GMTKN55 Benchmark (All), Basic Properties and Reactions of Small Systems (Sub1), Isomerizations and Reactions of Large Systems (Sub2), Barrier Heights (Sub3), Intermolecular Noncovalent Interactions (Sub4), and Intramolecular Noncovalent Interactions (Sub5).

	all	sub1	sub2	sub3	sub4	sub5
Hybrid DFAs
PBE0-D3(BJ)a	6.59	4.42	8.35	9.88	6.65	6.40
B3LYP-D3(BJ)a	6.37	4.25	10.21	9.04	5.56	5.68
ωB97X-Va	3.93	3.21	6.59	4.21	3.03	3.62
ωB97M-Vb	3.47	2.57	4.75	3.40	2.90	4.53
CF22-Dc	3.64	2.53	4.01	3.46	4.22	4.68
Machine-learned hybrid DFA
DM21d	3.97	1.99	4.64	3.63	6.56	4.16
B2PLYP-type double hybrids (bDHs)
DSD-BLYP-D3(BJ)b	3.07	1.84	4.3	3.04	3.92	3.15
B2GPPLYP-D3(BJ)b	3.26	1.95	4.59	3.24	4.28	3.21
XYG3-type double hybrids (xDHs)
XYG3e	3.75	1.72	4.69	2.23	6.04	4.88
XYGJ-OSe	4.04	4.04	1.85	4.42	2.94	6.01
xrevDSD-PBEB86-D4b	2.23	1.80	3.03	2.11	2.33	2.23
ωB97M(2)b	2.19	1.41	2.58	1.99	2.45	2.99
XYG7e	2.05	1.31	2.43	2.30	2.78	2.00
Renormalized xDHs (R-xDHs)
scsRPA	3.54	2.66	3.13	2.79	5.58	3.68
R-xDH7	2.23	1.74	3.09	2.48	2.80	1.55
R-xDH7-SCC15	2.24	1.77	3.05	2.54	2.80	1.55

^aResults from ref (37) using the basis set of def2-QZVPP.

^bResults from ref (22) using the basis set of def2-QZVPP.

^cResults from ref (49) using the basis set of def2-QZVPP.

^dResults from ref (50) using the basis set of def2-QZVPP.

^eResults from ref (36) using the numerical basis set of NAO-VCC-4Z.

Our R-xDH7 method attains an overall WTMAD2 of 2.23 kcal/mol for GMTKN55, placing it among the top class of computational methods in this benchmark. This performance underscores the efficacy of the renormalized PT2 in preserving the accuracy of PT2-based xDH methods across a broad range of chemical interactions, when dynamic correlations dominate. Furthermore, the R-xDH7 method demonstrates remarkable versatility in accurately modeling various types of interactions, including covalent bond interactions both in small (Sub1) and large systems (Sub2), barrier heights (Sub3), and nonbonded interactions (Sub4 and Sub5) in GMTKN55, as shown in Table 1. To extend our analysis, we followed the work of Liu and co-workers⁴⁹ and partitioned the 55 subsets of GMTKN55 into Radical7 (7 subsets) and Nonradical48 (48 subsets). This classification offered a focused lens through which to evaluate the performance of DFAs in reactions involving radical versus nonradical species. Supplementary Figure S1 in the Supporting Information suggests that R-xDH7, paralleling other state-of-the-art xDH methods, provides outstanding and balanced performance in both radical and nonradical systems. Remarkably, R-xDH7, also with 7 empirical parameters akin to XYG7, achieves this level of precision without resorting to any pairwise dispersion corrections, indicating the capabilities of renormalized PT2 correlation model for the description of nonbonded interactions.

Turning to the challenge of the static correlation, its significance grows substantially as molecules deviate from their ground state equilibrium geometries.^4,25,26 It is a notorious limitation that conventional DFAs struggle to accurately portray molecular bond dissociations, particularly when bonds are heavily stretched and the static correlation prevails due to (near)-degeneracy.⁴ As demonstrated in Figure 2a, lower-rung DFAs, such as GGA of PBE⁵¹ and the hybrid GGA of B3LYP,³⁸⁻⁴¹ exhibit significant static correlation errors. For instance, in the C–C bond dissociation of C₂H₆, these inaccuracies lead to deviations from the correct dissociation curves as large as 30 to 50 kcal/mol. PT2-based DH approximations, such as XYG7, fail badly; they tend to diverge at the dissociation limit, a direct consequence of PT2’s inherent inability to handle the degenerate situations.

The proposed R-xDH7 method successfully mitigates this divergence (Figure 2a). By integrating a spin-distinctive RPA-type renormalization into the PT2 model, R-xDH7 guides the C₂H₆ dissociation process toward the correct limit. Given its excellent performance on the GMTKN55 data set, R-xDH7 manifests its proficiency in effectively capturing a good portion of dynamic correlation and a substantial amount of the static correlation. However, an intriguing observation from Figure 2a reveals the persistence of the residual static correlation error in R-xDH7, which is particularly noticeable in the middle range of the dissociation curve, leading to an unphysical repulsive bump.

To further substantiate our findings, we compiled a comprehensive data set, MDB23–594, encompassing a total of 594 data points from 23 distinct bond dissociations in main-group molecules. This data set, detailed graphically in Figure 2b, includes 9 close-shell single-bond dissociations (CSD9–256), 8 multiple-bond dissociations (CMD8–204), and 6 open-shell systems (OBD6–134). Aiming to achieve an unbiased assessment, we partitioned the dissociation curves into three sections, namely equilibrium, middle and limit regions, respectively. As illustrated in Figure 2c, both XYG7 and R-xDH7 attain a good accuracy in the equilibrium region, being comparable to the expensive CCSD(T) method, which is considered the “gold standard” in quantum chemistry. However, as the static correlation effects intensifies moving from the equilibrium region to the middle and limit regions, their performances significantly degrade. The results from these 23 dissociation benchmarks confirm that R-xDH7 successfully overcomes the divergence problem observed in XYG7. However, it still exhibits mean absolute errors (MAEs) of 34.1 and 20.9 kcal/mol in the middle and limit regions, respectively. While these errors are notably reduced compared to other methods, including CCSD(T), they underscore the need for further improvement in order to accurately capture the static correlation on par with the accuracy being achieved by xDHs for the dynamic correlation.

In the realm of dispersion interactions as associated with, e.g., ωB97M(2)²² and xrevDSD-PBEB86-D4,³⁷ pairwise corrections with empirical parameters have proven to be highly effective.⁵²⁻⁵⁴ However, addressing static correlation errors poses a significantly greater challenge due to its complex multireference character.^55,56 Although current diagnostics, derived from both KS-DFT and wave function theory, often exhibit weak correlations with the static correlation,⁵⁷⁻⁵⁹ machine learning has emerged as a potent tool, offering innovative avenues to decipher complex correlation patterns embedded in data.^{49,50,60−63} Given that R-xDH7 has already captures a substantial portion of the static correlation, we anticipated that the residual errors, as those evident in the middle and limit regions for bond dissociations, could be rectified by devising a static correlation correction (SCC). Acknowledging that the static correlation is more pronounced yet less well understood than the dispersion interactions, we turned to machine learning. To precisely target both dynamic and static correlations for general purpose, we identified four system-independent input features at diverse theoretical levels as follows:

Electron-Pair Energy Ratios ({r_i})

Defined as 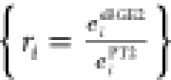, these ratios compare sBGE2^6,64 and PT2 correlation energies for each electron pair involved in double excitations. These electron pairs are sorted in descending order according to the sum of their eigenvalues, with each pair indexed by “i” to reflect its position in this ordered sequence. This descending order ensures that the electron pair with the largest sum of eigenvalues is considered first. Due to the nature that sBGE2 was designed to mitigate the PT2 divergence,^4,6,64 {r_i} were used to serve as an effective indicator for systems with significant static correlation. As evidenced in Supplementary Figure S2 in the Supporting Information, the distinct values of {r_i} accurately demarcated different dissociation regimes and displayed differing convergence tendencies with respect to the number of bonds being cleaved. This characteristic behavior forms a fundamental basis of our SCC pairwise correction.

HOMO–LUMO Gap (ΔE)

Calculated as the orbital energy difference between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the B3LYP method. As also evidenced in Supplementary Figure S2, ΔE was used to serve as a direct indicator of correlation effects across different dissociation regimes: a larger gap in the equilibrium region, a smaller gap in the middle region, and a near-degenerate gap in the limit region.

Exchange Energy Deviation (ΔE_x)

Represented as 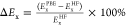. This metric was used to quantify the percentage difference between PBE and HF exchange energies. First introduced by Truhlar and colleagues^65,66 and also evidenced in Supplementary Figure S2, it is indicative of the extent of the static correlation effect within KS-DFT, with a larger difference pointing to a more important static correlation effect.

Response Functional Radii ({χ_α, χ_β})

These special radii of spin-pair distinctive response functions were used to provide insight into many-body static correlation effects. The detailed definition and implementation of {χ_α, χ_β} was provided in Supplementary Section S1. Our recent finding suggested that such effects in RPA-type correlation models are linked to the special radius of the KS noninteraction response function.^4,5 A radius exceeding unity would imply a divergence in the Dyson expansion of the RPA-like correlation, indicative of a strong static correlation effect beyond the scope of standard single-reference perturbation treatments.

Static correlation presents a unique challenge due to its elusive and ill-defined nature, as well as the scarcity of suitable data sets. To overcome these obstacles, we built here the MDB23–594 data set and devised a hybrid machine learning approach that combined symbolic and nonlinear parameter regression methods based on ({r_i}, ΔE, ΔE_x, {χ_α, χ_β}). As illustrated in Figure 1, we developed a systematic approach using the Sure Independence Screening and Sparsifying Operator (SISSO)⁶⁷ method. It allowed us to thoroughly explore the descriptor space and identify the most relevant descriptors for the residual static correlation errors associated with R-xDH. Consequently, we introduced a select number of parameters in a nonlinear fashion to refine and enhance the accuracy. The training process was iterative, continuing until the desired level of accuracy was reached using descriptors that displayed well-understood behaviors.

The final correction model, coined SCC15, is composed of two distinct parts, involving 9 descriptors and 15 empirical parameters:

2

The detailed formulation of the SCC15 model was provided in the Supporting Information. Briefly speaking, the first segment 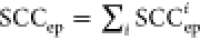represents the pairwise correction to the static correlation error, where “i” indexes each electron pair in double excitations. The second term SCC_mb addresses the residual many-body contributions beyond electron-pair excitations.

We started by focusing on R-xDH7’s errors in close-shell single-bond dissociations, where the relevant static correlation correction is pairwise and specific to the first electron pair: SCC¹_ep. We trained the SCC¹_ep model using the data set consisting of 131 data points from the first three reactions (S1–3) in CSD9–256, as shown in Figure 2b. Meanwhile, 1505 data points in GMTKN55 were also included, which served as constraints to preserve the good description of dynamic correlations of R-xDH7. To this stage, we arrived at the SCC¹_ep model with 3 descriptors {Dⁱ⁼¹_1–3} and 9 empirical parameters:

3

The 3 parameters {c_1–3} were concurrently determined alongside the 3 descriptors during the SISSO operation, while the remaining 6 nonlinear parameters {b_1–6} underwent iterative optimization in subsequent outer loops.

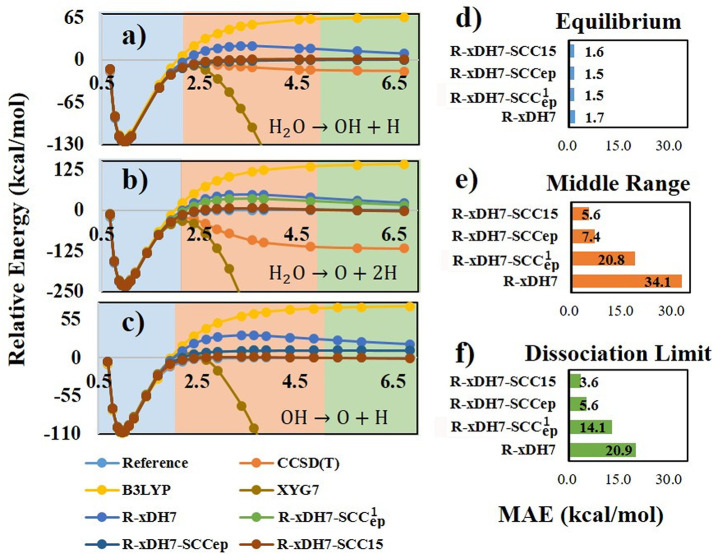
In Figure 3a–c, we present the calculated curves for three critical bond dissociations in H₂O, which were not part of the training sets used in this study. The results showed that the SCC¹_ep model notably improved R-xDH7’s performance in dissociating a single O–H bond from water (H₂O → OH + H); however, it fell short when simultaneously dissociating two O–H bonds (H₂O → O + 2H), as expected. For the comprehensive MBD23–594 data set, the MAEs of R-xDH7-SCC¹_ep in the middle region and dissociation limit were reduced to 20.8 and 14.1 kcal/mol, respectively, which marked a substantial progress compared to the uncorrected R-xDH7 method, although further improvement is needed to meet the desired accuracy comparable to that observed in the equilibrium region.

Figure 3.

Effect of different components of the R-xDH7-SCC15 method on three critical bond dissociation regions for H₂O (a–c) and on the MBD23–594 data set (d–f). B3LYP and CCSD(T) results are also presented for comparison in (a–c).

To extend the SCCⁱ_ep model for electron pairs beyond the first pair (i > 1), we then constructed a new training set comprising 118 data points from the first four reactions (M1–4) in CMD8–204. To maintain the success already achieved, constraints were imposed using data from GMTKN55 and also Reactions S1–3. Utilizing the hybrid regression approach led us to an interesting finding: the SCCⁱ_ep model with i > 1 shares two common descriptors with SCC¹_ep. Instead of reoptimizing the parameters established in the SCC¹_ep model, we introduced a novel parameter-descriptor pair {c₄, D₄} to recalibrate the static correlation correction for higher-order electron pairs. Then the form of the SCCⁱ_ep model was updated to

4

where {c₄, D₄} were optimized through a supplementary SISSO operation. Figure 3 vividly reveals that, by incorporating the static correlation correction for all electron pairs, the refined R-xDH7-SCCep approach accurately predicts the concurrent dissociation of both O–H bonds in the water molecule. It bears repeating that the three bond dissociation instances depicted in Figure 3 were neither part of the training set nor utilized as constraints for the SCCⁱ_ep model. A detailed depiction of bond dissociation curves for all 23 molecules can be found in the Supporting Information (Supplementary Figures S4–S26). A thorough analysis of these curves reveals that, R-xDH7, when augmented with the SCC_ep model, removes the undesired repulsive bump in the middle range of the dissociation curves.

Then we proceeded to develop the corresponding many-body static correlation correction model SCC_mb. We employed a training set comprising 81 data points from two reactions (O1–2) in OBD6–134 and one reaction (S9) in CSD9–256, as illustrated in Figure 2b. Consistently applying the same strategy, data from GMTKN55 and Reactions S1–3, along with M1–4 were included as constraints to minimize potential model bias or unintended influence on the outcomes. In light of the complex nature of many-body static correlation, the final SCC_mb model incorporates another 5 descriptors and their corresponding parameters, which were systematically identified and fine-tuned using the standard SISSO symbolic regression approach:

5

To this end, we arrived at the SCC15 model step by step, which is specifically adapted to R-xDH7.

As evident in Figure 3, the resultant R-xDH7-SCC15 method achieves a remarkably accurate description for all three types of bond dissociation processes involved in H₂O. Notably, within the MBD23–594 data set, 13 out of total 23 dissociation curves (over 300 distinct data points) were deliberately excluded from the training of the SCC15 model (see Figure 1). Deeper exploration within this expended framework further highlights the advancements brought forth by the R-xDH7-SCC15 method for the static correlation are indeed significant. The overall MAEs in the middle range and dissociation limit are now 5.6 and 3.6 kcal/mol, respectively, approaching to its performance in the equilibrium region (MAE = 1.6 kcal/mol) where the dynamic correction is dominant. Therefore, R-xDH7-SCC15 strikes an unprecedented balance between accurately capturing dynamic and static correlation effects. This conclusion is further reinforced by its high accuracy on the GMTKN55 data set. As detailed in Table 1, the overall MAE of R-xDH7-SCC15 for GMTKN55 is 2.24 kcal/mol. Upon examination across five subsets of GMTKN55, it is clear that the SCC15 model introduces, on average, an influence of less than 0.1 kcal/mol. Thus, the significant advancement of R-xDH7-SCC15 in describing strongly correlated systems is achieved without compromising its accuracy in describing dynamic correlations.

The MGCDB84 data set,⁶⁸ developed by the Head-Gordon group, represents a chemically diverse and comprehensive database designed for main-group chemistry. It encompasses 84 subsets containing a total of 4986 individual data points. Similar to GMTKN55, MGCDB84 primarily targets dynamic correlations with exception to 3 subsets denoted by the “MR” suffix.⁶⁸ Given the limited overlap of only 804 data points across 24 subsets shared by GMTKN55 and MGCDB84, we utilized the MGCDB84 data set as a supplementary means of validation. Supplementary Figure S3 in the Supporting Information suggests XYG7 and R-xDH7 as the top performers with MAEs of 0.65 and 0.67 kcal/mol, respectively. Notably, the SCC15 model shows a negligible effect on MGCDB84, with R-xDH7-SCC15 maintaining the good performance with an overall MAE of 0.67 kcal/mol. This consistency highlights the robustness and transferability of the predictive power of R-xDH7-SCC15.

While MGCDB84 is predominantly governed by the dynamic correlation outside the training set, we further evaluate the performance of R-xDH7-SCC15 on the MG23 set, which comprises 23 chemical reaction energies having important static correlation effects. These testing cases involve both main-group metal and nonmetal elements as detailed in Supplementary Table S1 in the Supporting Information, meticulously collected from prior literature sources^69,70 and identified using the %[(T)] diagnostic for their static correlation characters. While the CCSD(T) method yields an MAE of 4.03 kcal/mol, standard PT2-based methods, hampered by their inherent limitations in handling static correlation effects, demonstrate less accurate results. For instance, XYG7 records an MAE of 6.23 kcal/mol on the MG23 set. In sharp contrast, R-xDH7 effectively captures a significant portion of the static correlation with its innovative renormalized design, reducing the MAE to 2.96 kcal/mol. More significantly, R-xDH7-SCC15 achieves top-tier accuracy with an MAE of 2.43 kcal/mol on the MG23 set, underlining its superior potential to tackle problems with important static correlation effects.

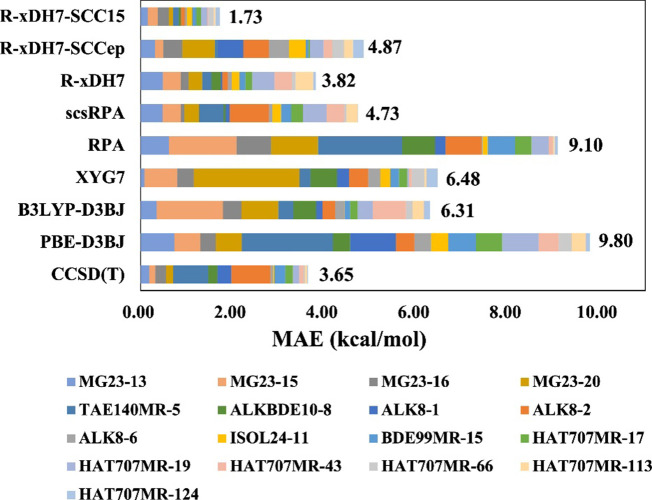
We would like to emphasize that the SCC15 model was devised to eliminate the residual errors adapted for R-xDH7 in the treatment of the static correlation. This point was substantiated by our findings: 4 out of 23 reactions in the MG23 test set exhibit SCC_ep, SCC_mb, or SCC15 values exceeding 3.0 kcal/mol. Extending this threshold across more than 6400 data points from GMTKN55, MGCDB84, and MG23 altogether, we identified and filtered out 17 specific chemical reactions which were detailed in Supplementary Table S2 in the Supporting Information. Figure 4 and Supplementary Table S2 show that R-xDH7 yields an MAE of 3.82 kcal/mol, which closely parallels the performance of the CCSD(T) method and significantly surpassed other DFAs. Significantly, none of these 17 reactions are part of training sets for the SCC15 model, yet R-xDH7-SCC15 achieves an outstanding performance with an MAE of only 1.73 kcal/mol, demonstrating again its remarkable robustness and transferability across a diverse spectrum of chemical scenarios. When applying only the electron-pair correction (i.e., R-xDH7-SCCep), the accuracy is inferior (MAE = 4.87 kcal/mol), highlighting the crucial interplay between electron-pair and many-body corrections in achieving optimal results. The success of the SCC15 model is rooted in its developing strategy that effectively tackled both types of static correlation errors, thereby providing strong evidence for the validity and effectiveness of our systematic approaches.

Figure 4.

Performance comparison of various methods on a specialized validation set of 17 reactions where the SCC15 model exhibits a substantial improvement (>3 kcal/mol). Each reaction is filtered out from the GMTKN55, MGDC84, or MG23 databases and identified by its corresponding subset name and original index. Details of these 17 reactions are presented in Supplementary Table S2.

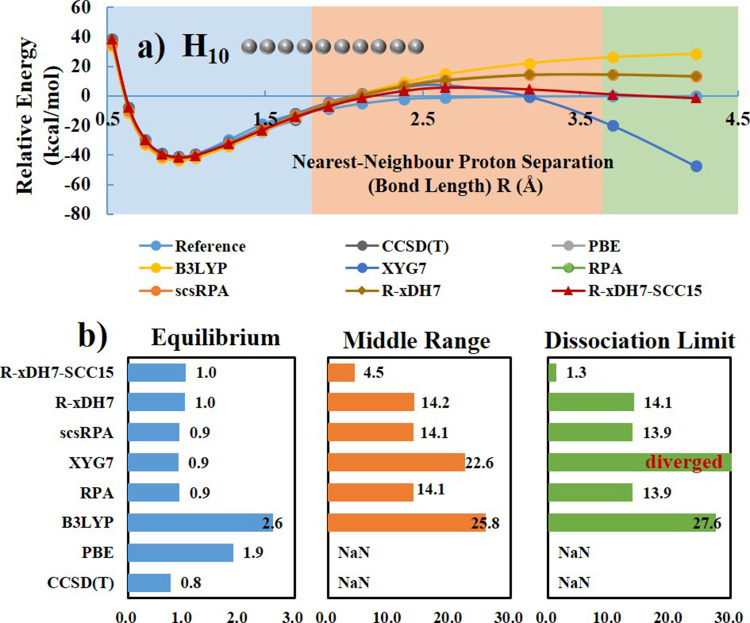
The linear hydrogen chain model holds a profound position within the realm of computational materials science,⁷¹ as it provides a pivotal means to mimic strong electron correlation effects, prevalent in many complex materials. Unlike the Hubbard model that simplifies interactions to one-dimensional lattice sites, the linear H chain model offers a more authentic depiction of molecular bonding inherent to condensed matter systems. Figure 5a presents the energy profile that dissociates all bonds simultaneously in a finite hydrogen chain consisting of ten atoms (H10), while Supplementary Table S5 provides the calculated energies per atom at the thermodynamic limit (TDL). This specific model system presents a stringent test, as it involves multiple bond dissociations simultaneously, being a far more challenging task compared to those usually encountered in typical molecules as in MBD23–594. R-xDH7-SCC15 demonstrates its robustness by providing a balanced and accurate description for the whole dissociation curve. As showcased in Figure 5b. the overall MAEs of R-xDH7-SCC15 in the middle range and dissociation limit are 4.5 and 1.3 kcal/mol, respectively, which are notably close to its performance in the equilibrium region (MAE = 1.0 kcal/mol), where the dynamic correction is dominant.

Figure 5.

Relative potential energy curve of H10. Energies per atom were evaluated by 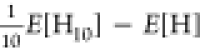(a) and Mean Absolute Errors (MAEs) of various methods across three critical regions: equilibrium, middle, and the dissociation limit (b). All calculations were performed employing the def2-QZVPP basis set. For benchmarking, accurate reference data were taken from ref (71). ‘NaN’ denotes failure of SCF convergence for PBE or non-convergence of coupled-cluster iteration for CCSD(T).

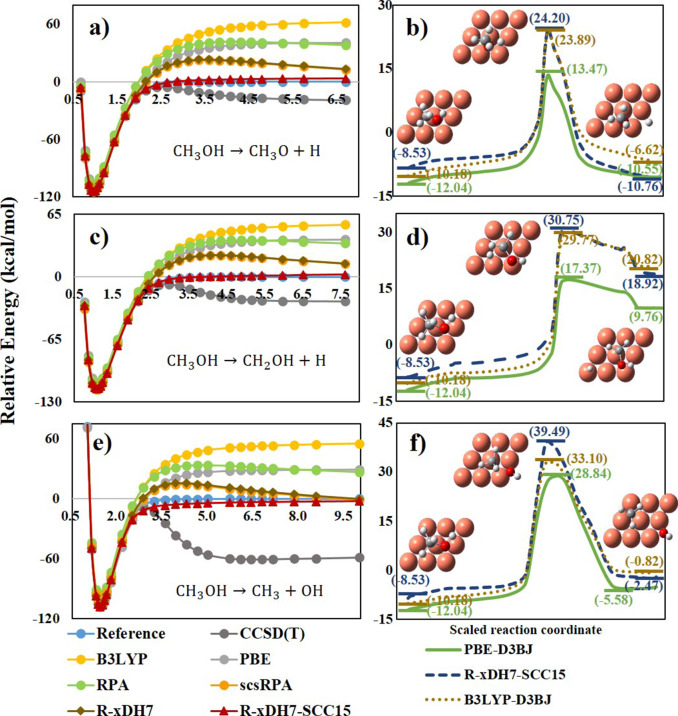
As a practical case study, we examined here the dissociative chemisorption of methanol (CH₃OH) on the Cu(111) surface, where three primary reaction channels are involved with the cleavage of O–H, C–H, and C–O bonds, respectively. The control of the product branching ratios via vibrational mode excitation has been proposed.^72,73 A proper description of these product branching ratios necessitates accurate molecular dynamics simulations, where constructing precise potential energy surfaces is essential. Until now, however, these surfaces have primarily been constructed at the GGA level.⁷²

First, we calculated the dissociation curves of methanol in the gas phase (Figure 6a,c, and e). Among the methods tested, R-xDH7-SCC15 performs significantly better with an MAE of only 1.91 kcal/mol against reference curves, outperforming traditional single-reference based methods such as conventional DFAs and even CCSD(T). We then extended our analysis to the bond dissociation curves of methanol on the Cu(111) surface by employing the XO-PBC strategy recently developed (See the Supporting Information for the detail of XO-PBC).⁷⁴⁻⁷⁶ Using R-xDH7-SCC15 results as the benchmark, we identified that the widely used GGA methods, in particular PBE-D3BJ,^52,54 have a strong tendency to overestimate the adsorption energies, while significantly underestimating reaction barriers. Figure 6b,d, and f show an improvement when utilizing the hybrid B3LYP-D3BJ method. For O–H and C–H bond dissociation pathways, the errors in B3LYP-D3BJ reaction barriers are less than 1 kcal/mol. However, the error exceeds 6 kcal/mol for C–O bond dissociation. Such discrepancies in predicted reaction barriers of different pathways are critical, as they have a direct impact on the determination of the product branching ratios, highlighting the need for more advanced computational approaches in an unbiased modeling of the complex surface reactions.

Figure 6.

Comparative analysis of the performance of various methods in calculating the dissociation processes of methanol (CH₃OH) in the gas phase (a,c, and e) and on the Cu(111) surface (b,d, and f).

In summary, we have developed the R-xDH7 functional that stands at the apex of Jacob’s Ladder of KS-DFT. This renormalized xDH method, containing seven empirical parameters, excels in capturing a significant portion of the static correlation, while preserving the generally good performance of xDH methods for a wide range of systems with the dynamic correlation. A pivotal achievement lies in the successful development of the SCC15 model through symbolic and parameter regressions to eliminate the residual static correlation errors associated with R-xDH7. The resultant R-xDH7-SCC15 method achieves an extraordinary balance in representing dynamic and static correlation effects over conventional DFAs, as well as the “gold standard” CCSD(T) in wave function theory. This superiority has been confirmed by extensive benchmarking over a diverse array of 6400 main-group chemical reactions sourced from GMTKN55, MGDCB84, and MG23 data sets, as well as 594 data points associated with 23 molecular dissociation curves. Applications of R-xDH7-SCC15 to the dissociative chemisorption of methanol on copper surfaces have showcased the inadequacies of the widely used GGAs, as well as hybrid DFAs, in accurately describing complex reaction energetics and kinetics. We anticipate that the R-xDH7-SCC15 method, integrating superior accuracy, high computational efficiency and black-box-like accessibility all-in-one, will significantly boost the predictive power of computational chemistry, particularly in elucidating intricate reaction mechanisms when both static and dynamic correlation effects are crucial.

Methods

The electronic calculations for R-xDH7-SCC15 were conducted using our in-house Rust-based Electronic Structure Toolkits (REST).²⁸ Unless specified otherwise, the def2-QZVPP basis set was employed. The resolution-of-identity approach was introduced in conjunction with the def2-SV(P)-JKFIT auxiliary basis set to enhance the computational efficiency. Only valence electrons from the outer shell were considered in the post self-consistent field (post-SCF) calculations. For the molecular dissociation curves, the calculations were performed without breaking spin symmetry. A detailed account of the computational parameters and methodology is provided in the SI. It is worth noting that the computational scaling of R-xDH7-SCC15 is on part with standard PT2-based doubly hybrid approximations. This is attributed to the advanced correlation models introduced, which exhibit the same or even lower computational scaling than the PT2 term. As illustrated in Table S8 in Supporting Information, the consumption cost of evaluating the PT2 correlations in XYG7 is comparable to a single B3LYP SCF iteration. This efficiency is particularly notable for large systems, as demonstrated by our calculations on systems comprising up to 80 atoms and over 3000 basis functions. Furthermore, the many-body renormalization of the PT2 evaluation and the SCC15 correction are cost-effective, similar to the standard PT2 term. This highlights the practicality of the R-xDH7-SCC15 method within the REST package for complex systems. While the REST package currently supports numerical evaluation of energy gradients for R-xDH7-SCC15, the development of analytic energy gradients is underway and will be a significant enhancement in the forthcoming versions of the package.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.4c00488.

• R-xDH7 functional, SCC15 model, and computational details (PDF)

• Geometry files for MBD23–594 and MG23 data sets and the surface reaction system of CH₃OH on Cu(111) (zip)

Author Contributions

CRediT: Yizhen Wang data curation, formal analysis, investigation, writing-original draft; Zihan Lin data curation, formal analysis, investigation; Runhai Ouyang data curation, formal analysis, funding acquisition, investigation; Bin Jiang data curation, formal analysis, funding acquisition, investigation; Igor Ying Zhang conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing-original draft, writing-review & editing; Xin Xu conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, writing-review & editing.

The authors declare no competing financial interest.