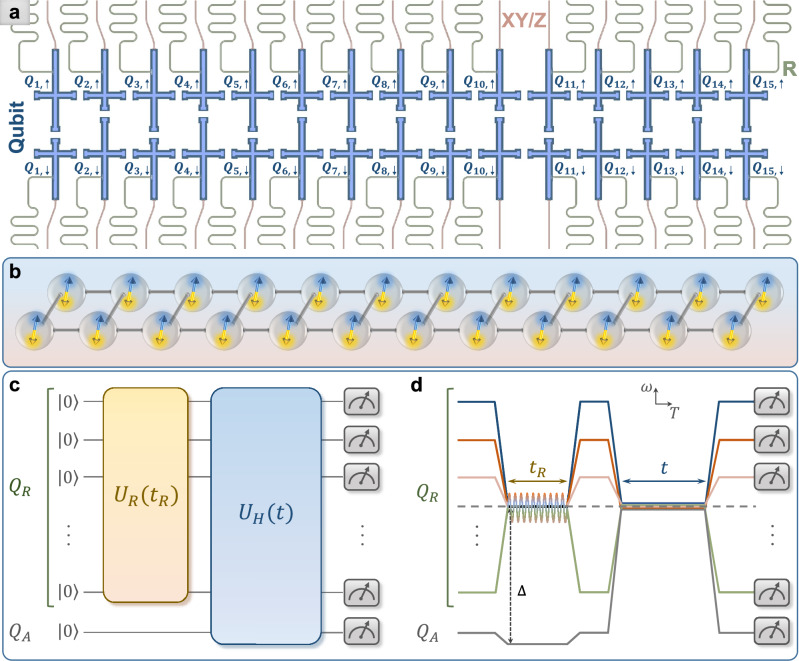
Fig. 1. Superconducting quantum simulator and experimental pulse sequences.

a The schematic showing the ladder-type superconducting quantum simulator, consisting of 30 qubits (the blue region), labeled Q_1,↑ to Q_15,↑, and Q_1,↓ to Q_15,↓. Each qubit is coupled to a separate readout resonator (the green region), and has an individual control line (the red region) for both the XY and Z controls. b Schematic diagram of the simulated 24 spins coupled in a ladder. The blue and yellow double arrows represent the infinite-temperature spin hydrodynamics without preference for spin orientations. c Schematic diagram of the quantum circuit for measuring the autocorrelation functions at infinite temperature. All qubits are initialized at the state $∣0⟩$. Subsequently, an analog quantum circuit ${\widehat{U}}_R\left(t_R\right)$ acts on the set of qubits Q_R to generate Haar-random states. This is followed by a time evolution of all qubits, i.e., ${\widehat{U}}_H\left(t\right)=\exp \left(-i\widehat{H}t\right)$ with $\widehat{H}$ being the Hamiltonian of the system, in which the properties of spin transport are of our interest. d Experimental pulse sequences corresponding to the quantum circuit in (c) displayed in the frequency (ω) versus time (T) domain. To realize ${\widehat{U}}_R\left(t_R\right)$, qubits in the set Q_R are tuned to the working point (dashed horizontal line) via Z pulses, and simultaneously, the resonant microwave pulses represented as the sinusoidal line are applied to Q_R through the XY control lines. Meanwhile, the qubit Q_A is detuned from the working point with a large value of the frequency gap Δ. To realize the subsequent evolution ${\widehat{U}}_H\left(t\right)$ with the Hamiltonian (1), all qubits are tuned to the working point.