Advancing forest carbon stocks’ mapping using a hierarchical approach with machine learning and satellite imagery

Abstract

Remote sensing of forests is a powerful tool for monitoring the biodiversity of ecosystems, maintaining general planning, and accounting for resources. Various sensors bring together heterogeneous data, and advanced machine learning methods enable their automatic handling in wide territories. Key forest properties usually under consideration in environmental studies include dominant species, tree age, height, basal area and timber stock. Being proxies of stand productivity, they can be utilized for forest carbon stock estimation to analyze forests’ status and proper climate change mitigation measures on a global scale. In this study, we aim to develop an effective machine learning-based pipeline for automatic carbon stock estimation using solely freely available and regularly updated satellite observations. We employed multispectral Sentinel-2 remote sensing data to predict forest structure characteristics and produce their detailed spatial maps. Using the Extreme Gradient Boosting (XGBoost) algorithm in classification and regression settings and management-level inventory data as reference measurements, we achieved quality of predictions of species equal to 0.75 according to the F1-score, and for stand age, height, and basal area, we achieved an accuracy of 0.75, 0.58 and 0.56, respectively, according to the R². We focused on the growing stock volume as the main proxy to estimate forest carbon stocks on the example of the stem pool. We explored two approaches: a direct approach and a hierarchical approach. The direct approach leverages the remote sensing data to create the target maps, and the hierarchical approach calculates the target forest properties using predicted inventory characteristics and conversion equations. We estimated stem carbon stock based on the same approach: from Earth observation imagery directly and using biomass and conversion factors developed for the northern regions. Thus, our study proposes an end-to-end solution for carbon stock estimations based on the complexation of inventory data at the forest stand level, Earth observation imagery, machine learning predictions and conversion equations for the region. The presented approach enables more robust and accurate large-scale assessments using limited annotated datasets.

Introduction

The organic carbon cycle is the main biogeochemical cycle on Earth^1,2. Among terrestrial ecosystems, forests are pivotal, representing one of the largest carbon reservoirs and, therefore, playing a critical role in the global carbon cycle^3,4. According to the IPCC Guidelines for National Greenhouse Gas Inventories⁵, methods for evaluating the carbon balance of forested lands and consequently tracking its changes over time can be broadly categorized into two groups: (1) assessment of changes in the carbon stocks of the main pools of ecosystems (2) assessment of gas flux rates to and from the atmosphere. While the carbon fluxes estimation is considered to be the direct method of measuring carbon exchange between land and atmosphere, it is not connected with the management practices and is poorly integrated into carbon sequestration support, being rather fundamental information of the ecosystem functioning⁶. Conversely, a balance estimation method based on tracking changes in carbon stocks is widely used from both scientific and practical standpoints, serving as the foundation for improved forest management and, consequently, implementing forest carbon offset projects^7,8.

By definition, total carbon stock in forest ecosystems is the amount of carbon that has been absorbed from the atmosphere and is currently stored in the ecosystem, primarily in living biomass and soil and, to a lesser extent, in dead wood and litter⁵. A significant advantage of carbon balance evaluation approaches based on the carbon stocks estimations is that they can be directly measured using relatively simple instruments, so they can be, therefore, monitored^9,10. In this regard, the task of estimating forest carbon balance can be solved by measuring the individual pools according to the main functional levels: the sum of above-ground and underground biomass, debris, litter, and soil, and a comparison of them at selected time points.

About 50% of the initial carbon uptake through photosynthesis is used by vegetation for growth and maintenance, while up to 70% from the overall forest carbon pool is stored in the biomass, mostly in woody parts¹¹. Consequently, under disturbances such as fires, logging and pest outbreaks, this storage becomes a source of emissions, along with, but to a lesser extent, areas of feelings and dead wood pool^12–14. From 20 to 60% of the total forest carbon can be sequestered in the soils^15,16. Soil carbon stabilized on a mineral matrix turns over more slowly than carbon from other pools, is more protected, and contributes significantly to the remaining carbon storage after fires and other events that result in significant loss of aboveground carbon^17,18. Assessing carbon stocks and their dynamics in soils is a highly relevant but rather complex and separate area of research¹⁹. Significantly, dependence between different pools is both compound and differentiated in space and time, such as, for instance, carbon stocks of the phytomass nonlinearly depend on the age of tree²⁰, while the data from long-term observations is required to establish patterns of forest growth dynamics²¹.

Forest stands are primarily characterized by the species they comprise and their growth specifics regarding the geography of the region²². One common methodological approach to assess forest carbon stocks is to use an integral parameter reflecting forest productivity—a growing stock volume—which can then be recalculated to other pools using Biomass Conversion and Expansion Factors²³. However, extensive accompanying structural information is still required to be considered to address the complexity of the mass distribution among pools. Apart from the conceptual complexity of the representation of biophysical processes behind stand productivity and the explanation of the principles of the distribution of the mass and energy in the carbon cycle, the additional difficulty of studying forest ecosystems is in their both temporal and spatial dynamics at extremely large extent²⁴. Therefore, approaches to upscaling the site-specific field monitoring data are of high need.

The development of Earth observation instruments has significantly simplified the process of estimating forest cover characteristics to a spatial extent. Openly available global products give a unique opportunity for the continuous spatial assessment and monitoring of vegetation communities worldwide^12,25,26. In addition to the widely known openly available satellite missions such as Sentinel-1,2, Landsat, and MODIS, specific remote sensing products for monitoring vegetation productivity directly have recently been employed, such as the Global Ecosystem Dynamics Investigation (GEDI) mission by the National Aeronautics and Space Administration of the USA and BIOMASS by the European Space Agency^27,28. Nonetheless, the significant drawbacks of these sources of information are their limited coverage and short-term lifespan, while approaches using ground assessments can give closer estimates of target characteristics^29,30.

Various research shows approaches to mapping forest stocks and their proxies from land inventory data, mostly field inventory plots and Earth observation imagery of medium resolution with and without additional sources of precise spatial data. Acquiring spatial information about the distribution of tree species is crucial for practice needs, biodiversity protection, and understanding carbon dynamics. Species mapping can achieve a high level of precision by combining machine learning (ML) approaches with inventory data and remote sensing^31–34. Another popular task is the spatial estimation of the growing stock volume, and aboveground biomass^35,36. The aboveground biomass changes can also be tracked directly from the Earth observation data²⁹. The possibility of prediction of the age of trees from inventory plots and forest-stand levels from Sentinel-2 data with and without the support of additional imagery sources such as airborne laser scanning was also demonstrated^37,38. A more complex task is the spatial modelling of forest structure, which can also be successfully solved using detailed land-based inventory. For instance, forest attribute maps were obtained from SAR Sentinel-1 and vegetation metrics from Sentinel-2 imagery based on measurements from field plots, giving accurate estimations of diameter at breast height, basal area, mean height, dominant height, wood volume, and canopy cover. Importantly, authors showed their height estimates overperformed the available GEDI dataset³⁰. These examples illustrate that combining land-based measurements and remote sensing data yields effective solutions for mapping forest structure characteristics at both local and regional scales, with classical ML algorithms are mostly in use. However, there is less exploration into employing inventory data at broader scales, such as the forest-stand level inventory, and opportunities for integrating computer vision techniques. One of the primary challenges in forestry studies is the absence of a standardized pipeline for estimating environmental characteristics through remote sensing and ML techniques. It is crucial to develop and integrate fully automated solutions into real-world applications that utilize freely available satellite data, eliminating the need for additional field-based observations or costly sensor systems.

In this study, we investigated the prediction of forest structure characteristics using Sentinel-2 data, annotated with forest management scale data, and a computer vision approach based on Extreme Gradient Boosting (XGBoost). Our objective was to integrate selected data sources to map essential forest structure characteristics across the complex boreal landscape. Within the same pipeline, we aimed to predict forest species, stand age, height, and basal area pixel-wise from imagery data. Growing stock volume and stem carbon stock were considered as target forest characteristics. To obtain this information from remote sensing observations, we proposed and compared two approaches: direct characteristic prediction from satellite imagery and a hierarchical approach for sequentially estimating intermediate forest parameters, followed by calculation using conversion factors. The experiments were conducted in the boreal forest of the Arkhangelsk region, Russia. The developed pipeline could be further implemented for other boreal regions and extended forest species. Our study makes the following main contributions:

• We proposed a hierarchical approach for the target forestry parameters—growing stock volume and stem carbon stock;

• For stem carbon stock estimation, we integrated the Biomass Conversion and Expansion Factor (BCEF) equation developed earlier²³ into an automated computation process, eliminating the need for field-based measurements or reliance on state forestry registers;

• We proposed and explored an automatic approach to simultaneously estimate forest age, height, timber stock, and basal area using a single ML-based pipeline;

• We collected and preprocessed a unique dataset, which included remote sensing imagery from Sentinel-2 and inventory data. This dataset was further utilized for the conversion and estimation of stem carbon stock.

Methods

The primary objective of this study is to propose a robust methodology for estimating growing stock volume and stem carbon stock in a fully automated manner utilizing freely available satellite observations. Ground truth data from forest inventory measurements collected in northern regions were utilized, incorporating all essential characteristics required for timber and carbon stock calculations. The data is structured at the stand level in a vector format that are georeferenced to align with satellite imagery. Inventory measurements encompass forest age, height, basal area, and dominant species.

To automatically extract these parameters from satellite images, a machine learning approach was employed. Regression and classification tasks were addressed at a pixel-wise level, associating each pixel from a satellite image with a corresponding forest stand description. Stem carbon stock was derived using a conversion formula based on key forest characteristics and predefined coefficients.

In addition to directly predicting carbon stock of selected pool from satellite images, a hierarchical approach was proposed. Intermediate parameters necessary for the conversion formula were predicted using separate ML models. These predicted maps were then integrated into the conversion formula to calculate carbon stock. This hierarchical method offers increased interpretability and facilitates a more comprehensive analysis by delineating the contribution of each forestry parameter to the final geo-spatial map.

For enhanced temporal analysis across various observation dates, the dataset was constructed using all available summer period images covering the study area.

We provide a detailed description of the data used and the numerical approaches employed. We outline the study area and describe the forest inventory data utilized and the ML pipeline within a supervised learning framework followed by conversion recalculations (Fig. 1). An approach to the accuracy assessment and the evaluation metrics used is also described.

Fig. 1.

Pipeline of presented approach.

Study area

The study area is located in the Arkhangelsk region, a region in northwestern Russia belonging to the European taiga (Fig. 2). The area is mostly covered by forests with Norway spruce (Picea abies Karst.) and Scots pine (Pinus sylvestris L.) among the predominant species, while the part of deciduous species in general does not exceed 20%.

Fig. 2.

Location of the study area and management-level inventory plots (in colour). The map was generated with the QGIS v.3.14 software (https://www.qgis.org) and base map from the open geographic database OpenStreetMap (https://www.openstreetmap.org).

The climate of the region is moderately continental. The average annual precipitation ranges from 380 to 700 mm. The active vegetation period, the number of days with a temperature above 10 °C, is approximately 100–110 days. The mean temperature of the warmest month (July) is $+16$ °C, and the coldest (January) is $-14$ °C. The terrain is characterised as a relatively flat plain that slopes towards the White Sea. Most of the main watershed plateaus and individual elevations rarely exceed 200–300 m above sea level^39,40.

Forest inventory data

In 2018, taxation data were obtained through forest inventory, utilizing a combination of measurement and decoding methods. These data are derived from field measurements. The total area of the surveyed territories is 126,641 hectares, and the corresponding map is provided in Fig. 2.

Forest inventory activities in the surveyed territories delineated the boundaries of forest stands (comprising homogenous areas in terms of composition and structure), and the following set of averages for each stand parameter was assessed: stand formula, age, height, and timber volume. In total, there were 12,617 stands in the surveyed territories, with areas ranging from 0.1 ha, the average stand area of 10 ha, and the median stand area of 5.6 ha.

To evaluate the performance of the ML pipeline, the dataset was divided into training and test sets. The test set represents a separate forest, modelling the prediction of target parameters on new territories. We further provide a more detailed description of all the forest parameters used.

Dominant species

The inventory data consists of forest species organized in a stand structure format. Forest stands are often heterogeneous, meaning that multiple species can be present within a single stand. As a result, each stand is characterized by either a single species or a combination of species, with a composition coefficient assigned to each. The specific spatial distribution of each species within a stand is usually unknown. A common approach involves assigning each stand a dominant species label, typically defined as the species with a proportion or composition coefficient exceeding 50%^22,41. While the study area encompasses several forest species, the subsequent analysis focuses solely on the most abundant representatives, including birch, aspen, spruce, and pine (Table 1).

Table 1.

Age groups for spruce, birch, aspen, and pine (division is based on the study²³).

Prevailing specimen	Young	Middle-aged	Immature	Mature
Spruce	Age $\le 40$	$40<$ age $\le 100$	$100<$ age $\le 120$	Age > 120
Birch	Age $\le 20$	$20<$ age $\le 40$	$40<$ age $\le 50$	Age > 50
Aspen	Age $\le 20$	$20<$ age $\le 30$	$30<$ age $\le 40$	Age > 40
Pine	Age $\le 40$	$40<$ age $\le 100$	$100<$ age $\le 120$	Age > 120

Mean stand age (years)

The forest age within a stand is an average parameter that is calculated based on model trees. A model tree is an average tree in terms of the measured diameter at breast height (DBH). The trees with DBH larger than 10 cm were taken into account in the taxation process for this study.

Mean stand height (m)

Mean stand height denotes the average height of the dominant part of the stand. The dominant part of the stand is associated with the weighted average height of the species presented in the stand, which involves the composition coefficients for the calculation.

Mean stand basal area (m²/ha)

Basal area was ascertained as a result of the taxation process and is the cross-sectional area of trees at breast height.

Mean stand timber stock (m³/ha)

This parameter is calculated as a multiplication of mean stand basal area to mean stand height⁴²:

$$\begin{array}{c}\hfill \text{Timber stock (GSV)}=\text{Basal area}·\text{Height}\end{array}$$ 1

Carbon mass (t C/ha)

In this study, we utilized a conventional formula proposed and verified in Ref.²³ to convert main forest inventory parameters into stem carbon stock. The equation was initially developed for major tree species of northern Eurasia and enables the processing of sample plot data for creating spatially distributed environmental maps. However, as previously mentioned, a significant limitation is the lack of necessary inventory data in many regions to perform such computations⁴³.

We, therefore, propose the integration of this equation into an end-to-end ML-based pipeline for carbon stock estimation using solely satellite-derived data instead of relying on state forest registers or field measurements. For this study, we tested only the stem pool. First of all, this data used for BCEF development was most accurately estimated at the plot level in the range of 92–94% according to the authors²³. At the same time, the aboveground biomass is largely represented by the stem; however, all forest biomass pools can be considered.

Another advantage of the selected approach for carbon computation is its tailored suitability for a wide range of northern regions with their specific environmental and climatic characteristics. Additionally, the coefficients can be updated for other geographical regions⁴⁴, making the proposed pipeline flexible for new territories and allowing for automation in forestry studies.

Therefore, based on the approach proposed in Ref.²³, the stem carbon mass per unit area (C) is calculated by utilizing information on growing stock volume per pixel (100 ${\text{m}}^2$). The equation employed for this estimation is given in Formula (2). In this formula, $\text{BCEF}(fr)$ denotes the biomass conversion and expansion factors (t/m$_{}^3$), which are conversion coefficients for recalculation of growing stock volume into the carbon stocks of different pools (stem, crown, roots, etc.) (denote as fr in the equation), and carbon content coefficient is the coefficient that depends on the leaf type, i.e. 0.5 if species belong to coniferous trees and 0.47 if species belong to deciduous trees, the specific values are shown in Table 2. In the present study, the stem fraction was considered according to the age groups given in Table 1. The detailed values for the BCEF coefficients for the stem fraction for the Northern taiga zone are presented in Table 3.

$$\begin{array}{c}\hfill \text{Carbon mass}=\text{GSV}·\text{BCEF}(fr)·\text{Carbon content coefficient}\end{array}$$ 2

Table 2.

Carbon content coefficients. Values for spruce, birch, aspen and pine are taken from study²³.

Prevailing specimen	Spruce	Birch	Aspen	Pine
Carbon content coefficients	0.5	0.47	0.47	0.5

Table 3.

Biomass conversion and expansion factors (t/m$_{}^3$) (BCEF) values for the stem fraction for the considered forest species of different age groups in the Northern taiga zone according to²³.

Prevailing specimen	Spruce	Pine	Aspen	Birch
Young	0.421	0.414	0.403	0.534
Middle-aged	0.444	0.426	0.426	0.530
Immature	0.450	0.443	0.431	0.537
Mature	0.447	0.460	0.444	0.528

Remote sensing data

In our research, we utilized multispectral Sentinel-2 data that underwent Level-2A (L2A) preprocessing, which incorporates atmospheric correction. The imagery was obtained via the Copernicus Open Access Hub⁴⁵. We specifically employed 10 spectral bands (B02, B03, B04, B05, B06, B07, B08, B8A, B11, B12) with varying spatial resolutions of 10 and 20 meters. To ensure consistency, we upscaled images from channels B05, B06, B07, B8A, B11, and B12-originally at 20 m resolution to 10 m using the nearest neighbor interpolation method. The georeferenced multispectral imagery has the format of digital numbers (denote the surface reflectance) with pixel values of the raw data in the range from 0 to ${10}^4$.

A forest cover mask, generated using the deep learning (DL) method described in the previous study⁴⁶, was applied to each Sentinel-2 image. This process filtered out areas devoid of forest cover, such as roads, lakes, and lawns.

As additional features for forest characteristics prediction, we also computed a number of vegetation indices, namely Normalized Difference Vegetation Index (NDVI), Enhanced Vegetation Index (EVI) and Green Normalized Difference Index (GNDVI). A more detailed description of each of these indices is provided in Table 4. They are known as significant additional information for environmental tasks using both raw satellite data and ML algorithms for ecosystem analysis⁴⁷.

Table 4.

Vegetation indices considered in the study.

Abbreviation	Name	Definition	Sentinel 2 formula
NDVI	Normalized Difference Vegetation Index	$\frac{\text{NIR}-\text{RED}}{\text{NIR}+\text{RED}}$	$\frac{\text{B08}-\text{B04}}{\text{B08}+\text{B04}}$
EVI	Enhanced Vegetation Index	$2.5.\frac{\text{NIR}-\text{RED}}{\text{NIR}+6.\text{RED}-7.5.\text{BLUE}}$	$2.5.\frac{\text{B08}-\text{B04}}{\text{B08}+6.\text{B04}-7.5.\text{B02}}$
GNDVI	Green Normalized Difference Index	$\frac{\text{NIR - [540nm:570nm]}}{\text{NIR + [540nm:570nm]}}$	$\frac{\text{B09}-\text{B03}}{\text{B09}+\text{B03}}$

All accessible images were manually chosen based on two criteria: the absence of cloud cover (the percentage of cloud cover less than 10%) and the months corresponding to the vegetation period (June, July, August, and September) for the years 2018–2020. This selection yielded eight dates: 2018-07-30, 2018-08-04, 2018-08-27, 2018-09-11, 2019-06-08, 2019-06-13, 2020-06-04, and 2020-07-09. The age map was modified for each subsequent year by incrementing the values in the initial map corresponding to the year of the field inventory measurements.

XGBoost models

XGBoost, short for Extreme Gradient Boosting, stands out as a powerful ensemble learning algorithm renowned for its exceptional performance in both classification and regression tasks⁴⁸. This algorithm is widely used for environmental studies and can be considered as one of the conventional choices for methodology assessment in ecological analysis⁴⁹. As a classifier, XGBoost constructs a multitude of decision trees sequentially, where each subsequent tree corrects the errors of its predecessors, gradually improving predictive accuracy. It employs a gradient boosting framework, wherein each tree is trained to minimize the residual errors of the previous tree, effectively enhancing the model’s ability to capture complex relationships within the data. Moreover, XGBoost incorporates regularization techniques to prevent overfitting, thereby ensuring robust generalization to unseen data. Similarly, as a regressor, XGBoost leverages its boosting mechanism to optimize the sum of squared residuals, iteratively refining predictions by adding subsequent trees. Its ability to handle missing values, feature importance analysis, and parallel computing make it a versatile and highly sought-after tool in ML tasks, offering state-of-the-art performance across diverse datasets and applications. In our study, we utilized the XGBoost classifier to classify dominant species, while the regressor model was trained for other characteristics, such as age, height, and basal area.

Experiments

The forest inventory data, initially in vector format, was converted into a raster format based on the resolution of Sentinel-2 imagery (10 m per pixel). Consequently, each pixel within an individual forest stand was assigned a single label for classification or a numerical value for regression analysis. Given the heterogeneous nature of vegetation cover, even within a single forest stand, diverse spectral characteristics exist among different components of the same stand. This diversity enhances the dataset compared to methods that treat an individual stand as an indivisible forestry unit. Moreover, this chosen approach eliminates the necessity of delineating stand boundaries to make predictions for new areas, which may not always be feasible and poses additional challenges for further environmental analysis.

Given the severe imbalance in the species target, which was the sole classification target, a process was initiated to address this issue. The crops of $128\times 128$ pixels were extracted from the species raster mask, and their class distribution was evaluated. Subsequently, a patch-based manual revision was conducted to ensure a more balanced representation of species within each patch. Similarly, corresponding patches that match the Sentinel-2 patches were selected. This approach ensured consistency in the data distribution across all targets, whereby data reduction was carried out based on the species target classification. The resulting dataset was further balanced using the undersampling method to even out species target class. The ultimate distribution of the target parameters is presented in Fig. 3. The division into training and testing subsets was conducted randomly in an 80/20 proportion, respectively, without overlap.

Fig. 3.

Dataset overview. (a) Dominant species (b) Age (c) Carbon stock (d) Height (e) Basal area (f) Timber stock. The frequency denotes the number of pixels of Sentinel-2 images corresponding to the forest stands with a particular value or class of the observed forest parameter.

Then, a table was compiled for the training of individual models for each forest parameter: forest age, height, basal area, timber stock, and stem carbon stock. In each row of the table in CSV format, pixel values for each channel were included, along with the values of three vegetation indices for a given date, resulting in a total of 13 features. Pixel values for all other dates were added to the separate tables, while the same training and testing splitting for all forest parameters were preserved. Therefore, we conducted individual experiments for each observation date to perform a comprehensive analysis of model prediction for the studied forestry parameters.

Overall, individual models were trained for each parameter, namely age, species, height, basal area, volume, and carbon stock for each collected observation date of Sentinel-2 satellite. It allows us to reach optimal hyperparameters for each target forestry characteristic. We also conduct experiments with a set of different tunable parameters in the XGBoost model: number of estimators, depth, maximum number of nodes, and learning rate. These parameters were tuned using Randomized Paramaters Opimization method. The results for the best parameters were then performed for each target forestry characteristic. Additionally, a hierarchical approach involving the sequential computation of final maps for growing stock volume and carbon stock from their constituents was explored. This involved deriving timber volume from basal area and height, from Formula (1), and carbon stock from age, species, height, and basal area, from the conversion Formula (2). These experiments are denoted as “Timber (hierarchical)” and “Carbon stock (hierarchical)”, while the baseline approach with the direct prediction of these parameters from Sentinel-2 images is denoted as “direct” in the further experiments.

Metrics

The following metrics were used for quality check in regression tasks: $\text{MAPE}$ (Mean Absolute Percentage Error), $\text{RMSE}$ (Root of Mean Squared Error), $\text{MAE}$ (Mean Absolute Error), and $R^2$ (Coefficient of Determination). One of the most important metrics is $\text{MAPE}$ due to its stronger interpretability for target users such as foresters.

All metrics were computed on a per-pixel basis. If $\widehat{y_i}$ is the predicted value of the i-th pixel and $y_i$ is the corresponding true value, then the MAPE, RMSE, MAE and $R^2$ estimated over $n_{\text{pixels}}$ are defined as follows (here $\epsilon$ is an arbitrary small yet strictly positive number to avoid undefined results when y is zero):

$$\begin{array}{c}\hfill \text{MAPE}(y,\widehat{y})=\frac{1}{n_{\text{pixels}}}\sum _{i=1}^{n_{\text{pixels}}}\frac{\left|y_i,-,{\widehat{y}}_i\right|}{max\left(\epsilon ,,,\left|y_i\right|\right)}\\ \hfill \text{RMSE}(y,\widehat{y})=\sqrt{\frac{1}{n_{\text{pixels}}}\sum _{i=1}^{n_{\text{pixels}}}{\left(y_i,-,{\widehat{y}}_i\right)}^2}\\ \hfill \text{MAE}(y,\widehat{y})=\frac{1}{n_{\text{pixels}}}\sum _{i=1}^{n_{\text{pixels}}}\left|y_i,-,{\widehat{y}}_i\right|\\ \hfill R^2(y,\widehat{y})=1-\frac{{\sum }_{i=1}^{\text{pixels}}{\left(y_i,-,{\widehat{y}}_i\right)}^2}{{\sum }_{i=1}^{\text{pixels}}{\left(y_i,-,\overline{y}\right)}^2}\text{, where}\overline{y}=\frac{1}{n_{\text{pixels}}}\sum _{i=1}^{n_{\text{pixels}}}{y}_i\end{array}$$

To report the quality of the forest specimen classification task, we used precision, recall, and ${\text{F}}_1$-score with macro averaging (averaging the value of the metrics per class). This approach increased the sensitivity of these metrics to errors for rare classes. Precision for a given class is defined as $P=\frac{\mathit{TP}}{TP+FP}$, recall as $R=\frac{\mathit{TP}}{TP+FN}$, where TP denotes a number of true positives, FP is a number of false positives, and FN is a number of false negatives. ${\text{F}}_1$-score is the harmonic mean of precision and recall: ${\text{F}}_1=2\frac{P·R}{P+R}$.

Results

In this study, we investigated various methods for estimating forest carbon stock and key intermediate forest parameters. Our approach involved integrating ML algorithms to identify correlations between multispectral patterns and forestry characteristics. We employed a hierarchical approach, defining the ultimate environmental characteristic of carbon stock using a set of intermediate models. Subsequently, we trained multiple models to estimate forest dominant species, age, and basal area. To achieve this, we utilized a preprocessed set of Sentinel-2 images covering the study area during a predefined summer period. Each intermediate parameter model was trained and validated independently to optimize hyperparameter values. For our experiments, we selected the XGBoost algorithm as it is commonly used for handling tabular data in environmental studies.

Tables 5, 7, 8, 9, 11, 10, 12, and 13 provide outcomes for the direct prediction of individual forest parameters, including species, age, height, basal area, volume, and carbon stock, respectively. While Tables 6 and 14 provide summary of the results across all dates.

Table 5.

Resulting macro-averaged metrics for dominant forest species prediction (spruce, birch, pine, aspen) on the test subset for different observation dates.

Test date	Precision	Recall	${\text{F}}_1$-score
2018-07-30	0.74	0.74	0.74
2018-08-04	0.75	0.75	0.75
2018-08-27	0.75	0.75	0.75
2018-09-11	0.74	0.74	0.74
2019-06-08	0.76	0.76	0.76
2019-06-13	0.75	0.75	0.75
2020-06-04	0.75	0.75	0.75
2020-07-09	0.75	0.75	0.75
Average	0.75	0.75	0.75

Table 7.

Resulting metrics for forest age estimation on the test subset for different observation dates.

	MAPE	MAE (years)	RMSE (years)	${\text{R}}^2$
2018-07-30	0.201	11.74	16.66	0.73
2018-08-04	0.199	11.65	16.52	0.74
2018-08-27	0.206	11.93	16.85	0.72
2018-09-11	0.223	12.91	17.81	0.69
2019-06-08	0.181	10.39	15.06	0.78
2019-06-13	0.180	10.34	14.99	0.78
2020-06-04	0.179	10.34	14.98	0.78
2020-07-09	0.192	11.07	15.99	0.75
Average	0.195	11.3	16.1	0.75

Table 8.

Resulting metrics for forest height estimation on the test subset for different observation dates.

	MAPE	MAE (m)	RMSE (m)	${\text{R}}^2$
2018-07-30	0.162	1.95	2.69	0.58
2018-08-04	0.160	1.92	2.66	0.59
2018-08-27	0.167	1.99	2.72	0.57
2018-09-11	0.179	2.13	2.88	0.52
2019-06-08	0.155	1.84	2.59	0.61
2019-06-13	0.156	1.86	2.59	0.61
2020-06-04	0.156	1.85	2.59	0.61
2020-07-09	0.157	1.87	2.62	0.60
Average	0.161	1.9	2.7	0.58

Table 9.

Resulting metrics for forest basal area estimation on the test subset for different observation dates.

	MAPE	MAE $(\frac{{\text{m}}^2}{\text{ha}})$	RMSE $(\frac{{\text{m}}^2}{\text{ha}})$	${\text{R}}^2$
2018-07-30	0.163	1.81	2.37	0.54
2018-08-04	0.159	1.75	2.31	0.56
2018-08-27	0.168	1.84	2.41	0.52
2018-09-11	0.179	1.94	2.54	0.47
2019-06-08	0.146	1.60	2.15	0.62
2019-06-13	0.154	1.68	2.24	0.59
2020-06-04	0.154	1.68	2.24	0.59
2020-07-09	0.155	1.70	2.25	0.58
Average	0.160	1.75	2.3	0.56

Table 11.

Resulting metrics for the hierarchical approach for timber volume estimation on the test subset for different observation dates.

	MAPE	MAE $(\frac{{\text{m}}^3}{\text{ha}})$	RMSE $(\frac{{\text{m}}^3}{\text{ha}})$	${\text{R}}^2$
2018-07-30	0.394	51.66	67.87	0.55
2018-08-04	0.387	50.07	66.48	0.57
2018-08-27	0.407	51.97	68.19	0.54
2018-09-11	0.445	55.21	71.87	0.49
2019-06-08	0.366	46.53	62.93	0.61
2019-06-13	0.377	47.90	64.07	0.60
2020-06-04	0.377	47.90	64.07	0.60
2020-07-09	0.379	48.42	64.67	0.59
Average	0.391	49.9	66.3	0.57

Table 10.

Resulting metrics for the direct approach for timber volume estimation from Sentinel-2 imagery on the test subset for different observation dates.

	MAPE	MAE $(\frac{{\text{m}}^3}{\text{ha}})$	RMSE $(\frac{{\text{m}}^3}{\text{ha}})$	${\text{R}}^2$
2018-07-30	0.371	51.59	68.05	0.55
2018-08-04	0.397	53.36	69.95	0.52
2018-08-27	0.410	54.74	71.15	0.51
2018-09-11	0.455	59.01	75.57	0.44
2019-06-08	0.380	50.17	66.92	0.56
2019-06-13	0.385	50.79	67.29	0.56
2020-06-04	0.423	55.70	72.93	0.48
2020-07-09	0.393	52.02	68.99	0.53
Average	0.402	53.4	70.11	0.52

Table 12.

Resulting metrics for the direct approach for carbon stock estimation on the test subset for different observation dates.

	MAPE	MAE $(\frac{\text{t C}}{\text{ha}})$	RMSE $(\frac{\text{t C}}{\text{ha}})$	${\text{R}}^2$
2018-07-30	0.374	15.43	20.03	0.50
2018-08-04	0.373	15.13	19.82	0.51
2018-08-27	0.380	15.41	19.95	0.50
2018-09-11	0.423	16.56	21.21	0.44
2019-06-08	0.355	14.08	18.64	0.57
2019-06-13	0.359	14.30	18.82	0.56
2020-06-04	0.398	15.77	20.55	0.47
2020-07-09	0.374	14.84	19.48	0.53
Average	0.380	15.19	19.81	0.51

Table 13.

Resulting metrics for the hierarchical approach for carbon stock estimation from Sentinel-2 imagery on the test subset for different observation dates.

	MAPE	MAE $(\frac{\text{t C}}{\text{ha}})$	RMSE $(\frac{\text{t C}}{\text{ha}})$	${\text{R}}^2$
2018-07-30	0.368	15.21	19.84	0.51
2018-08-04	0.362	14.82	19.05	0.53
2018-08-27	0.343	15.20	19.74	0.51
2018-09-11	0.406	16.06	20.73	0.46
2019-06-08	0.340	12.69	18.24	0.58
2019-06-13	0.350	14.08	18.60	0.57
2020-06-04	0.363	14.89	19.71	0.52
2020-07-09	0.358	14.37	19.00	0.55
Average	0.361	14.67	19.36	0.53

Table 6.

Resulting metrics for dominant forest species estimation on the test subset.

Specimen	Precision	Recall	${\text{F}}_1$-score
Spruce	0.74	0.67	0.70
Birch	0.78	0.84	0.81
Pine	0.83	0.88	0.85
Aspen	0.66	0.59	0.62
Average	0.75	0.75	0.75

Table 14.

Resulting metrics for all considered forest parameters on the test subset. Average metrics for all observation dates are reported.

	MAPE	MAE	RMSE	${\text{R}}^2$
Age	0.195	11.3 years	16.1 years	0.75
Height	0.161	1.9 m	2.7 m	0.58
Basal area	0.160	1.7 $\frac{{\text{m}}^2}{\text{ha}}$	2.3 $\frac{{\text{m}}^2}{\text{ha}}$	0.56
Timber stock (direct)	0.402	53.4 $\frac{{\text{m}}^3}{\text{ha}}$	70.1 $\frac{{\text{m}}^3}{\text{ha}}$	0.52
Timber stock (hierarchical)	0.391	49.9 $\frac{{\text{m}}^3}{\text{ha}}$	67.9 $\frac{{\text{m}}^3}{\text{ha}}$	0.57
Carbon stock (direct)	0.380	15.19 $\frac{\text{t C}}{\text{ha}}$	19.81 $\frac{\text{t C}}{\text{ha}}$	0.51
Carbon stock (hierarchical)	0.361	14.67 $\frac{\text{t C}}{\text{ha}}$	19.36 $\frac{\text{t C}}{\text{ha}}$	0.53

Table 5 presents the results for dominant forest species estimation. We focused on four main species that were most abundant in the study area. Pine achieved the highest F1-score of 0.85, followed by birch with an F1-score of 0.81. Distinguishing spruce and aspen from other forest classes proved more challenging, resulting in F1-scores of 0.72 and 0.62, respectively. The overall quality of the species classification model on the test subset is 0.75. The created maps are shown in Figs. 4 and 10.

Fig. 4.

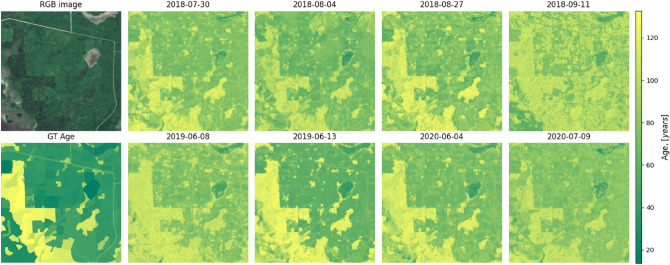
Example of dominant forest species predictions for different testing dates. RGB image (Sentinel-2), ground truth (GT), and predictions for each date are the windows of $512\times 512$ px ($5.12\times 5.15$ km). The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 10.

Example of dominant forest species prediction. The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

For the regression task, we developed models for forest age, height, basal area, and timber stock estimation. In addition to directly predicting timber stock based on satellite imagery and vegetation indices, we also computed timber stock using a formula involving predicted forest age, species, and basal area. The results are detailed in Tables 7, 8 and 9. The forest age model achieved an R2 value of 0.75 on the test subset, with a MAPE of 0.195. The height model yielded an average R2 value of 0.58 and a more accurate MAPE of 0.161. Basal area estimation resulted in a MAPE of 0.16. For the visual assessment, the created maps for different observation dates are shown in Figs. 5, 6 and 7. The examples for one of the forestry are shown in Figs. 11, 12 and 13.

Fig. 5.

Example of forest age predictions for different testing dates. RGB image (Sentinel-2), ground truth (GT), and predictions for each date are the windows of $512\times 512$ px ($5.12\times 5.15$ km). The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 6.

Example of forest height predictions for different testing dates. RGB image (Sentinel-2), ground truth (GT), and predictions for each date are the window of $512\times 512$ px ($5.12\times 5.15$ km). The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 7.

Example of forest basal area predictions for different testing dates. RGB image (Sentinel-2), ground truth (GT), and predictions for each date is the window of $512\times 512$ px ($5.12\times 5.15$ km). The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 11.

Example of forest age prediction. The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 12.

Example of forest height prediction. The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 13.

Example of basal area prediction. The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

We explored two approaches for estimating timber stock using ML algorithms: direct mapping from remote sensing data and prediction based on intermediate forestry parameters such as age and dominant species, followed by calculation using a formula. Both approaches yielded a MAPE of 0.39 and R2 of 0.57 for the hierarchical approach outperforming the direct approach with the MAPE of 0.402 and R2 of 0.52. The achieved metrics align with the required range of error and thus show its further applicability in carbon stock estimation in forests. The example of created maps is presented in Figs. 8 and 14.

Fig. 8.

Example of timber stock predictions based on the hierarchical approach for different testing dates. RGB image (Sentinel-2), ground truth (GT) and predictions for each date are the windows of $512\times 512$ px ($5.12\times 5.15$ km). The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 14.

Example of timber stock prediction based on the hierarchical approach. The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

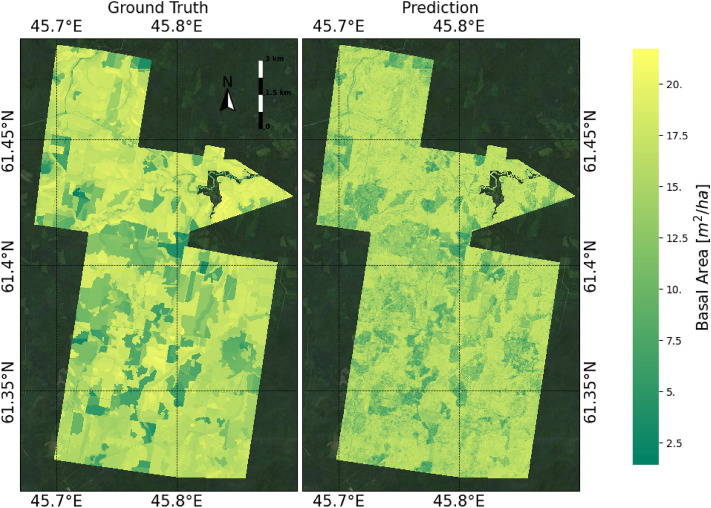
Our primary focus was on evaluating carbon stock as the ultimate forestry parameter. We considered both direct mapping from satellite images and calculation by formula, similar to the approach used for timber stock estimation. Interestingly, the hierarchical approach outperformed direct mapping for carbon stock estimation, achieving an R2 value of 0.53 compared to 0.51 for direct mapping. The ground truth values and created maps are shown in Figs. 9 and 15. The ultimate MAPE for the hierarchical approach is 0.361 (Fig. 10) (Tables 10, 11, 12, 13, 14).

Fig. 9.

Example of carbon stock predictions based on the hierarchical approach for different testing dates. RGB image (Sentinel-2), ground truth (GT) and predictions for each date is the window of $512\times 512$ px ($5.12\times 5.15$ km). The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Fig. 15.

Example of carbon stock prediction based on the hierarchical approach. The figure is created by the authors using Matplotlib library version 3.7.2 (https://matplotlib.org/) on Python 3.11 version, Sentinel-2 RGB composite derived from Copernicus Open Access Hub (https://scihub.copernicus.eu/) is chosen for visualization.

Discussion

Forests are a significant sink of carbon greenhouse gases (GHG) from the atmosphere, partly mitigating the negative impacts of anthropogenic GHG emissions on the climate⁵⁰. As an ecosystem, forests are also a source of biodiversity, providing habitats for many species of birds, vertebrates, invertebrates and microorganisms and conditions for their survival and development⁵¹. In this regard, the importance of introducing sustainable forestry management practices and developing tools for supporting forest ecosystem functioning is crucial in the era of highly destructive pressure on nature, while spatial monitoring systems are considered to be the core technology. The dissemination of updating open-source Earth remote sensing data and the development of artificial intelligence methods make it possible to move to spatial assessments and, thereby, clarify forest structure characteristics important for both practical management and ecosystem services estimations. Among data analysis and prognosis methods, applied ML solutions help to organize semi-automated operational monitoring systems in the most effective way due to the relevant simplicity in implementation and computational efficiency at rising technology advancements⁵², while related products can be used for global-scale and local-scale assessments⁵³. The core limitation of the development of ML-based solutions is the training data is supposed to meet essential criteria: to be balanced, to be rich enough to provide the ability of the model to generalise over unseen information and to be representative of the target phenomena, considering that ML-algorithms are black-boxes, lack in physical meaning^54,55. In the context of environmental processes and ecosystem dynamics, meeting the mentioned requirements necessitates specialised approaches.

Forest structure characteristics are the proxies for both biodiversity and climate-related ecosystem functioning of forests. Due to technical difficulties and labour and resource intensity, ground-based measurement data is fragmented, while large-scale forest assessments and carbon balance estimates currently use aggregated data from taxation surveys conducted over limited areas. Since forests are such a pivotal carbon sink, uncertainties associated with forest dynamics bring a large gap in our understanding of global biosphere response to environmental changes^56,57. Forest aboveground biomass is rarely measured both in the field or through remote sensing and is usually estimated from tree-level assessments through the structure data such as stem diameter, total tree height, wood density and others, while the importance of proper allometric equations better account for local biomass specificity is highlighted⁵⁸. We proposed a pipeline for estimating key forest characteristics using satellite data, eliminating the need for field-based measurements. This approach can significantly facilitate the ecological assessment of extensive territories. It is crucial that these parameters are predicted within a unified setup, ensuring the consistency of the remote sensing data in terms of observation dates and spectral and spatial resolution. Future studies could also benefit from integrating additional augmentation techniques focused on multispectral satellite data⁵⁹.

Based on both visual and numerical assessments, we observed a high alignment between the model predictions and ground truth values. Our evaluation of model performance across different observation dates revealed notable consistency, particularly in forest species classification, where the F1-score remained consistently high across all observed images. In the regression task, the most robust results were obtained for carbon stock estimation within the hierarchical experimental setup. It is worth noting that the predicted results for all parameters differed significantly for the considered autumn imagery (2018.09.11), resulting in lower numerical performance. As a recommendation, it may be advisable to exclude autumn images or apply corrections to such data. Overall, the summer images proved to be more informative for estimating target values and extracting significant spectral patterns from Sentinel-2 images (Fig. 11).

The hierarchical setup allows model training for each parameter independently. It helps to improve further interpretability of achieved results by calculating metrics for each of intermediate parameter. Moreover, in case of availability of particular parameter, we can substitute it in the calculation pipeline improving the quality of the carbon stock estimation. For instance, the height maps can be available for particular regions from LiDAR-based measurements or can be obtained from high-resolution RGB images. Therefore, the proposed approach supports higher flexibility preserving the structure of the forestry inventory data and intermediate components. Also, for each parameter, different ML or DL algorithms can be employed.

While hierarchical approaches are slower than direct methods, they offer robustness and better metrics. Parameters like timber and carbon stock are derived through complex formulas and are often rough estimations. By using algorithms that independently calculate simpler parameters such as height, species, and basal area, ML models can adapt more effectively through active learning and retraining. Hierarchical methods provide a more interpretable framework, helping to identify the contributions of various factors to model performance. Though direct methods may be faster, they often lack the nuanced understanding that hierarchical approaches capture. This layered approach leads to more accurate and generalizable models, especially in complex ecological and environmental applications. In summary, despite their computational demands, hierarchical approaches offer significant advantages in robustness, adaptability, and interpretability. These benefits make them valuable tools for improving remote sensing models for monitoring the environment. We will continue to refine our methods, using both hierarchical and direct approaches to advance the field and enhance sustainable forest management tools.

In this study, we used an approach to separate the prediction of target variables, which is a common practice in related research based on the data from inventory plots, however, all of the predicted characteristics are tightly connected with each other. Corresponding algorithmic techniques can be therefore considered as promising, such as multitask architectures, allowing the capture of both inter-feature and geo-spatial dependencies^60,61, which can enhance physical meaning to the data-driven solutions. Introducing different sources of inventory data into multitask architectures, including spatially explicit stand-level information, could be an additional challenge worth exploring.

The ultimate applicability of prediction solutions is, first of all, driven by the accuracy of predictions, which, apart from the training procedure, is mostly driven by the quality of the input data. Being widely spread in the forest inventory, especially applicable in management practices⁶², stand-level data has both advantages and disadvantages. Logically, it provides more data than plot-level observations, representing homogenous stands over the areas reaching dozens and hundreds of hectares. At the same time, controlling the associated uncertainties due to measurement errors in the field inventory data or changes from both natural and artificial reasons is limited due to the absence of detailed investigations within the stand-level units. From this perspective, the transition to more detailed spatial maps is a promising shift to obtaining the information previously unavailable for all target variables. As for the accuracy procedure itself, a question arises as to how to properly provide it with input data representing large areas while output data gives a detailed picture of the area pixel-wise. In this study, we employ a pixel-wise approach for both model training and validation. This method involves treating each pixel as an independent entity to predict the target value. Consequently, a group of pixels from the same individual forest stand is treated as distinct entities with different features despite sharing the same label. An alternative approach involves processing an entire forest stand by aggregating all pixels within its boundaries, as proposed in Ref.³⁸. While this approach offers an objective assessment of an indivisible forest unit, its main limitation is the requirement for a map of forest stands for new regions, which may not always be accessible (Fig. 12).

Importantly, when supported with additional field investigations to ensure obtained detailed spatial predictions, resulting spatial maps could serve as unique benchmark data for new algorithm training. The main objective of this study was the development of the general pipeline for timber and carbon stock estimation based on ML technique and satellite observations, therefore, we utilized a single ML algorithm to assess the feasibility of the proposed pipeline. XGBoost is a common choice for environmental tasks⁴⁹. Future studies will employ other ML and DL algorithms to advance the methodology.

Conclusion

Estimation of forest carbon stock is a complex task due to the numerous components involved in its calculation. Field-based measurements are generally considered a reliable source of such information, but they are often time-consuming and labor-intensive, particularly for large areas. To overcome this challenge, remote sensing data is crucial in supporting environmental studies across diverse regions with varying biodiversity. The integration of ML algorithms in data processing has proven to be highly beneficial for such tasks, although there is no universally accepted pipeline for addressing these issues.

In this study, we propose a hierarchical pipeline for estimating carbon stock that involves multiple stages based on integrating ML techniques and multispectral satellite data. The initial steps focus on estimating key forest characteristics such as dominant species, forest age, height, and basal area. Subsequently, we compare two methods for timber stock estimation: direct prediction from satellite imagery versus a calculation based on intermediate parameters predicted in earlier stages. Similarly, carbon stock estimation is performed using the same approach.

Our results demonstrate that the hierachical approach for both timber stock and carbon stock estimation outperforms the direct prediction of the final parameter. This methodology can be extended to other regions, allowing for the independent substitution and enhancement of intermediate ML models and input data. Overall, this approach shows promise for environmental studies and efficient forest management practices (Figs. 13, 14, 15).

Author contributions

Conceptualization, S.I.; methodology, S.I., P.T.; software, I.S.; validation, I.S., S.I. and P.T.; formal analysis, I.S., S.I., P.T. and A.E.; investigation, all authors; resources, E.B.; data curation, I.S., S.I.; writing—original draft preparation, all authors; writing—review and editing, all authors; visualization, I.S., P.T.; supervision, E.B.; project administration, D.S.; funding acquisition, E.B. All authors reviewed the manuscript.

Data availability

The datasets used and analysed during the current study available from the corresponding author on reasonable request.