Machine learning model to predict rate constants for sonochemical degradation of organic pollutants

Abstract

In this study, machine learning (ML) algorithms were employed to predict the pseudo-1st-order reaction rate constants for the sonochemical degradation of aqueous organic pollutants under various conditions. A total of 618 sets of data, including ultrasonic, solution, and pollutant characteristics, were collected from 89 previous studies. Considering the difference between the electrical power (P_ele) and calorimetric power (P_cal), the collected data were divided into two groups: data with P_ele and data with P_cal. Eight input variables, including frequency, power density, pH, temperature, initial concentration, solubility, vapor pressure, and octanol–water partition coefficient (K_ow), and one target variable of the degradation rate constant, were selected for ML. Statistical analysis was conducted, and outliers were determined separately for the two groups. ML models, including random forest (RF), extreme gradient boosting (XGB), and light gradient boosting machine (LGB), were used to predict the pseudo-1st-order reaction rate constants for the removal of aqueous pollutants. The prediction performance of the ML models was evaluated using different metrics, including the root mean squared error (RMSE), mean absolute error (MAE), and R squared (R²). A significantly higher prediction performance was obtained using data without outliers and augmented data. Consequently, all the applied ML models could be used to predict the sonochemical degradation of aqueous pollutants, and the XGB model showed the highest accuracy in predicting the rate constants. In addition, the power density and frequency were the most influential factors among the eight input variables in prediction with the Shapley additive explanation (SHAP) values method. The degradation rate constants of the two pollutants over a wide frequency range (20–1,000 kHz) were predicted using the trained ML model (XGB) and the prediction results were analyzed.

1. Introduction

With rapid advancements in computer processing capabilities and algorithmic methodologies, effective machine learning (ML) and deep learning (DL) algorithms have been developed and applied in numerous domains, such as healthcare, finance, autonomous driving, and sound analysis [1], [2], [3], [4], [5], [6], [7]. Environmental engineering researchers have begun applying these techniques for data analytics. Since the late 2010 s, extensive ML research has been conducted, with most studies focusing on air pollution monitoring and water quality management [8], [9], [10], [11], [12].

Over the last two decades, advanced oxidation processes (AOPs) have been widely investigated for the removal of recalcitrant and emerging pollutants using electromagnetic and mechanical wave energies and a variety of oxidizing chemicals and catalysts [13], [14], [15], [16], [17], [18]. Recent advancements in ML have led to the development of AOPs for investigating various process variables from new perspectives and predicting pollutant removal [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29]. The ML-based approach is expected to streamline experimental processes by reducing time and obviating extensive chemical- and labor-based experiments [19], [20]. By analyzing and training experimental data collected from previous research, pollutant degradation (removal efficiencies and reaction rate constants) can be predicted using a well-trained ML algorithm. Recently, researchers have reported the application of ML techniques to ultrasound-based AOPs. Zhou et al. predicted pseudo-1st-order reaction rate constants for the removal of pharmaceuticals in sonoelectrochemical processes using various ML models. They selected 15 input variables, including six electro-oxidation features, two ultrasonic features, four pollutant features, and three environmental features [21]. A research group investigated ML models to predict the tetracycline removal rate in sonophotocatalytic processes using various catalysts. They developed ML algorithms with tetracycline concentration, catalyst dose, irradiation time, light power, ultrasound on/off, and additive oxidant concentration as input variables [22], [23], [30]. Glienke et al. obtained experimental data for the degradation of 32 phenol derivatives using an 860 kHz sonoreactor and analyzed the data using various ML models [31]. All the above-mentioned sonochemists used only their own experimental data, relatively small numbers of datasets compared to those in previous AOPs research, for ML training and evaluating ML performance.

This study aims to investigate the applicability of ML to sonochemistry using datasets collected from previous studies. Three well-known ML models, random forest (RF), extreme gradient boosting (XGB), and light gradient boosting machine (LGB), were used to predict the pseudo-1st-order reaction rate constants of sonochemical pollutant degradation. A total of 618 datasets from 89 previous research papers, providing a comprehensive understanding of sonochemical degradation, were used for the training of the ML models. Eight input variables, including frequency, power density, pH, temperature, initial concentration, solubility, vapor pressure, and octanol–water partition coefficient (K_ow), and one target variable of the degradation rate, constant were considered. Different metrics, including the root mean squared error (RMSE), mean absolute error (MAE), and R squared (R²), were analyzed and compared to evaluate the performance of the ML models. In addition, the rate constants for the removal of two selected pollutants (naphthol blue black and phenol), which are the most frequently reported pollutants in our collected data, under various frequency conditions (20–1,000 kHz) were predicted using the trained ML model.

2. Experiment and analytical methodology

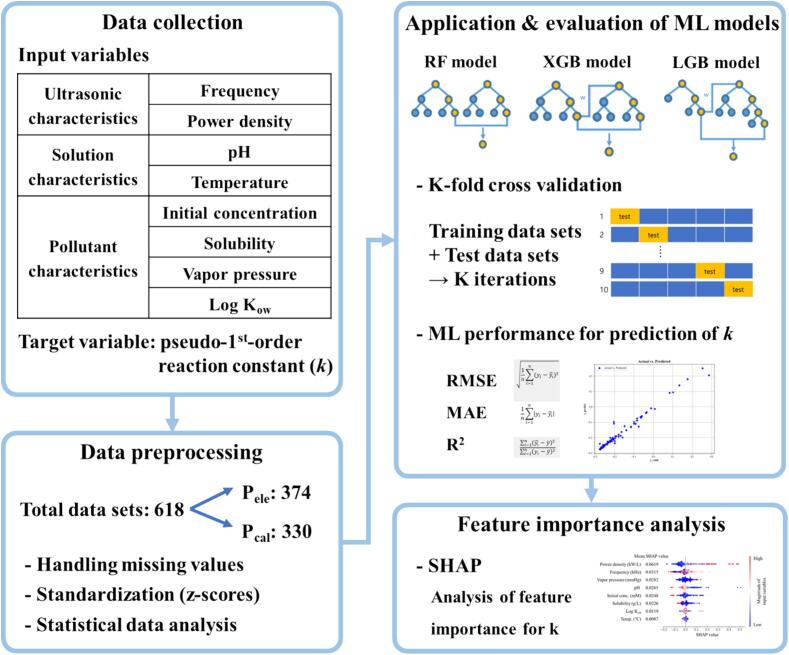
A brief flowchart for the ML using data from previous research on sonochemical processes in this study is shown in Fig. 1. A desktop computer for office (Intel i7-8700 CPU 3.20 GHz; RAM 16 GB) was used in this study.

Fig. 1.

Flow chart for machine learning using data from previous research on sonochemical processes.

2.1. Data collection

A literature search was conducted using bibliographic databases such as Google Scholar with five major keywords: “sonochemical,” ”degradation,” “ultrasound,” ”ultrasonic,” and “oxidation.” This search yielded 618 sets of data from 89 articles published since 2000 on the degradation of aqueous pollutants in sonochemical processes using only ultrasound, but not other AOPs. Each dataset included eight input variables, namely frequency, power density, pH, temperature, initial concentration, solubility, vapor pressure, and octanol–water partition coefficient (K_ow), and one target variable of the pseudo-1st-order reaction rate constant for the removal of pollutants was collected considering the ultrasonic, solution, and pollutant characteristics. Some rate constants were obtained from the figures of research papers using a high-resolution monitor (QHD 2560 × 1440) and PlotDigitizer software (https://plotdigitizer.com/) [32], [33]. Some data on pollutant characteristics were obtained from well-known websites, such as PubChem (https://pubchem.ncbi.nlm.nih.gov/) and the Toxin and Toxin Target Database (T3DB, https://www.t3db.ca/). The collected data with a reference list was provided in the Supplementary Material. In spite of relatively larger numbers of datasets compared to those in previous research, more datasets should be added to enhance diversity in datasets [21], [22], [23], [30], [31]. In addition, it should be noted that the geometric effects were not considered in this study because most previous researchers rarely reported the details of the geometric conditions in their studies. Recently, it has been reported that small changes in the geometric conditions could result in significant differences in sonochemical activity [34], [35], [36], [37], [38], [39].

2.2. Data preprocessing

In sonochemistry, information on the input power for ultrasound irradiation is provided in terms of electrical power (P_ele), which represents the energy consumed by the ultrasound generator, or calorimetric power (P_cal), which represents the heat energy induced by the absorption of ultrasound in a liquid medium. It has been reported that the difference between electrical power and calorimetric power is quite significant and P_cal typically ranges from 45 to 85 % of P_ele depending on the applied ultrasonic system [35], [36], [39]. Previous researchers provided either P_cal or P_ele in their studies. Thus, the collected datasets were divided into two categories [data with P_ele (374 sets) and data with P_cal (330 sets)] and analyzed separately. In addition, considering the size (or volume) difference of the sonoreactors, the power density (P_ele or P_cal / liquid volume) was used instead of P_ele or P_cal.

Some data, including temperature, pH, solubility, vapor pressure, and log K_ow, were not available, and missing data were replaced to obtain complete ML datasets. The temperature and pH were assumed as 25℃ and 6, respectively. Missing values of solubility, vapor pressure, and log K_ow were appropriately estimated based on related references and the reliable data we collected [40], [41].

By statistically analyzing the datasets, outliers, whose values were higher or lower than three standard deviations of each variable were determined [42], [43], [44] and the total data were divided into two groups and analyzed using ML models: data including the outliers and data excluding the outliers. It has been reported that more accurate results can be obtained for predicting target values using data without outliers in ML algorithms [42], [44], [45], [46].

As the final step in data preprocessing for ML training, the data were standardized to have a mean of zero and a standard deviation of one using z-scores, owing to the large differences in the magnitudes of the variables [47], [48], [49], [50]. The preprocessed data were then partitioned into training and validation data using K-fold cross validation (K=10) to prevent overfitting of the ML models [47], [48], [49].

2.3. Model experiment(construction)

ML models, including RF, XGB, and LGB, which are commonly used in the application of ML models in various fields, were used in this study [20], [26], [27], [28], [29], [50], [51], [52]. In our preliminary tests, relatively poor prediction accuracies were obtained using Linear, Ridge and Lasso regression models. All the programs for running the ML models were implemented using Python (ver. 3.10.13) and the Scikit_learn (ver. 1.3.0), xgboost (ver. 1.7.3), and LightGBM (ver. 4.0.0) libraries were used. The hyperparameters of the applied ML models were optimized using tree-structured Parzen Estimator algorithm, RMSE, and cross validation results. The optimized hyperparameter values for XGB, LGB, and RF were shown in Table 1S [53], [54].

Table 1.

Model performance evaluation metrics.

Evaluation metrics	Mathematical expressions
Root Mean Squared Error (RMSE)	$\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$
Mean Absolute Error (MAE)	$\frac{1}{n}{\sum }_{i=1}^n\left|y_i-\widehat{y_i}\right|$
R Squared (R2)	$\frac{{\sum }_{i=1}^n{\left(\widehat{y_i}-\overline{y}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}$

2.4. Performance evaluation metrics

The accuracies of the ML models were evaluated using MAE, RMSE, and R², also known as the coefficient of determination (Table 1) [55], [56]. MAE represents the average absolute error between the predicted and actual values, and RMSE is the square root of the mean squared error (MSE), which is the average of the squared errors. The MAE and RMSE values closer to 0 indicate higher prediction performance. The R² value reflects how well the generated model explains the data for both the actual and predicted values, with a value closer to 1 indicating a higher model performance.

Furthermore, the SHAP value method was employed to analyze the contribution of each input variable to the predicted target variable. SHAP assigns a 'SHAPley value' to each input variable (or feature), precisely measuring the contribution of individual variable to the model output in comparison to a baseline prediction—the mean prediction in the data. These values play a pivotal role in understanding the impact of specific features on the predictive decisions of a model [57].

3. Result and discussion

3.1. Statistical analysis of collected data

Table 2, Table 3 show the results of a simple statistical analysis of the collected data, including the outliers [eight input variables: frequency, power density, pH, temperature, initial concentration, solubility, vapor pressure, and octanol–water partition coefficient (K_ow); one target variable: pseudo-1st-order reaction rate constant] with P_ele and P_cal, respectively. Table 2S and 3S depict the statistical analysis results without outliers. Fig. 1S–4S also show the histogram plots of data with P_ele including the outliers (374 sets), data with P_ele excluding the outliers (326 sets), data with P_cal including the outliers (330 sets), and data with P_cal excluding the outliers (275 sets). Although many more datasets for the ultrasonic degradation of organic pollutants under a wide range of experimental conditions were collected compared to previous research [22], [31], [58], the data were not distributed evenly, which could lead to low accuracies in the predicted target values using the developed ML algorithms for the input variables in the untrained or poorly trained ranges.

Table 2.

Descriptive statistics of the collected data with P_ele (374 sets) (the outliers were included).

	Frequency (kHz)	Power density (kW/L)	pH	Temp.	Initial conc. (mM)	Solubility (g/L)	Log Kow	Vapor pressure (mmHg)	Rate constants (×10-3/sec)
mean	358	0.82	5.92	22.8	2.25	12.88	2.64	0.25	0.72
std	283	2.92	1.87	5.59	28.34	47.9	1.80	1.31	1.23
min	20	8 × 10–5	2.0	10	3.67 × 10–5	1.30 × 10–6	−1.20	2.40 × 10–13	7.56 × 10–5
25 %	200	0.16	5.5	20	0.01	0.04	1.46	4.74 × 10–6	0.16
50 %	300	0.24	6.0	23.5	0.03	0.2	2.9	9.01 × 10–5	0.39
75 %	497	0.48	6.5	25	0.10	4.3	3.83	3.08 × 10–3	0.90
max	1,700	50	13.0	80	545.9	818	6.91	12.0	19.19

Table 3.

Descriptive statistics of the collected data with P_cal (330 sets) (the outliers were included).

	Frequency (kHz)	Power density (kW/L)	pH	Temp.	Initial conc. (mM)	Solubility (g/L)	Log Kow	Vapor pressure (mmHg)	Rate constants (×10-3/sec)
mean	432	0.47	5.84	24.6	1.11	15.67	2.74	16.66	1.24
std	396	1.79	1.96	9.59	6.42	53.64	2.03	69.08	4.42
min	20	0.02	2.0	1	4.76 × 10–5	1.30 × 10–6	−9.7	2.57 × 10–12	7.56 × 10–5
25 %	35	0.08	5.5	20	26.7 × 10–3	0.02	1.94	6.68 × 10–6	0.08
50 %	404	0.15	6.0	25	0.086	0.50	2.9	9.01 × 10–5	0.23
75 %	600	0.25	7.0	25	0.5	10	3.83	0.087	0.78
max	1,700	12.6	12.7	70	100	717	6.91	297	44.33

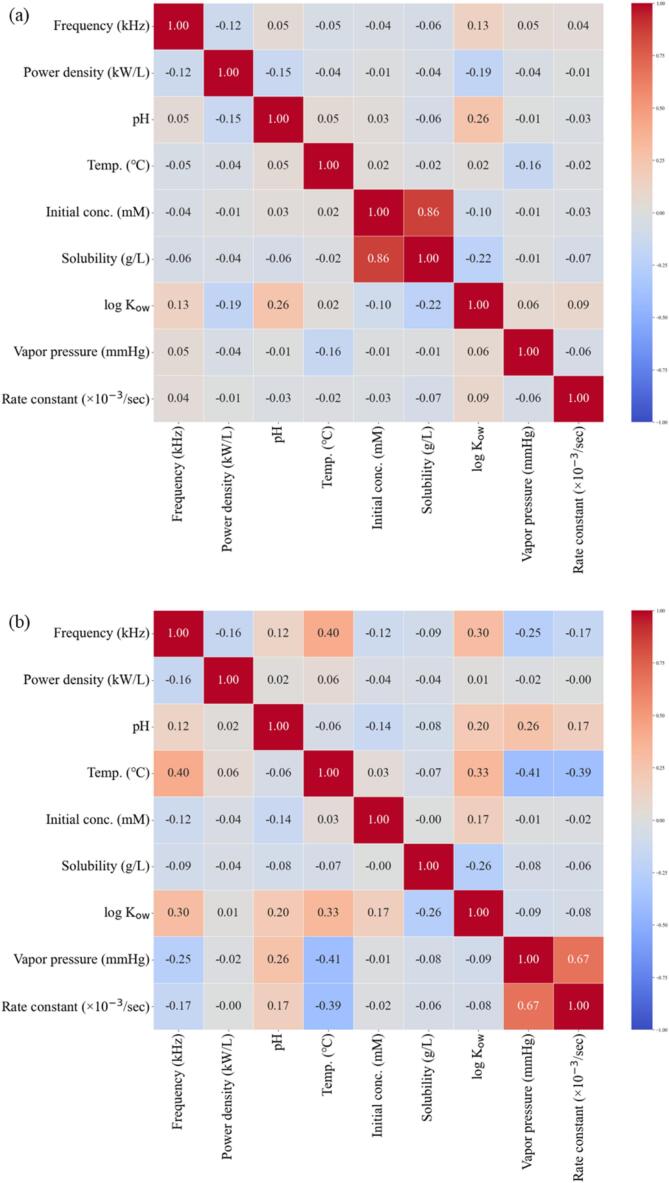
Before the ML analysis, the linear relationship between the variables was investigated using Pearson correlation with the data including the outliers as shown in Fig. 2. The Pearson correlation coefficient ranges from −1.00 to + 1.00 and represents the strength and direction of the linear relationship between two variables [19], [25], [59]. Most variables in the collected data did not demonstrate a linear relationship. For the data with P_cal, a relatively strong linear relationship between vapor pressure and rate constant was obtained, which could be due to the presence of large outliers [the maximum vapor pressure was 10¹⁵ times higher than the minimum pressure (malachite green: 2.4 × 10^–13 mmHg; carbon disulfide: 297 mmHg)]. As shown in Fig. 5S(b), a weak linear relationship between the vapor pressure and rate constant was obtained using data that excluded outliers.

Fig. 2.

Pearson correlation matrix of eight input variables and one target variable: a) data with P_ele including the outliers, b) data with P_cal including the outliers.

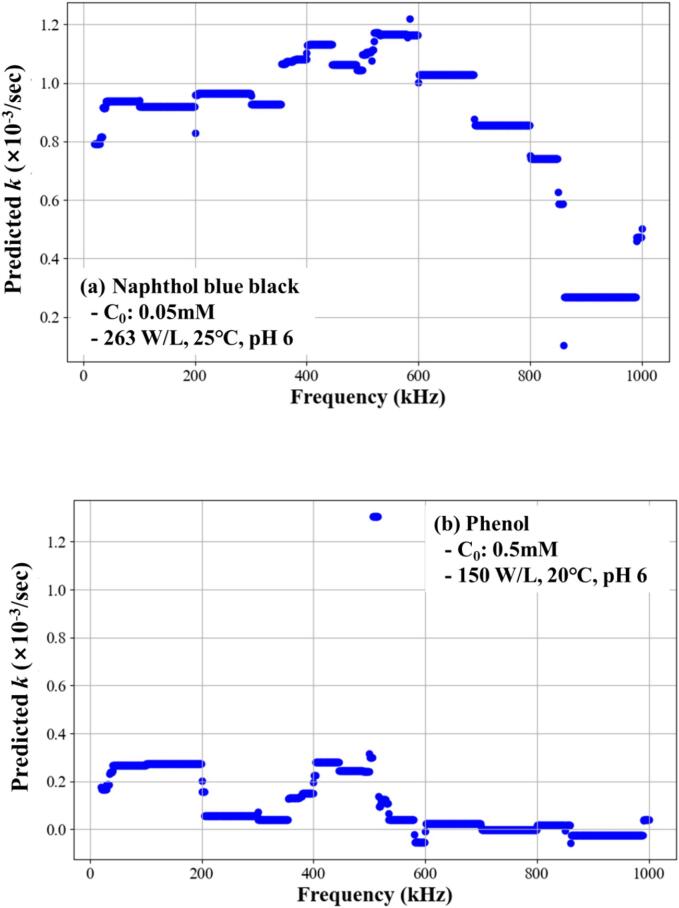
Fig. 5.

Predicted pseudo-1st-order reaction kinetic constants for the sonochemical degradation of naphthol blue black or phenol under various frequency conditions (20 to 1,000 kHz) using the XGB model with the augmented data.

ML algorithms are widely recognized for their ability to handle nonlinear relationships and offer more flexible solutions when the data distribution is unknown or nonnormal. Therefore, given the limitations of simple statistical methods in providing valuable conclusions, we opted for ML methods to analyze our data further [47]. The feature engineering techniques were not used in this study because of relatively small number of features [60], [61], [62].

3.2. Comparison of generated models

The performance of the trained ML models was evaluated for the prediction of rate constants based on their accuracy for four types of data using the evaluation metrics of RMSE, MAE, and R²: 1) data with P_ele including the outliers (374 sets), 2) data with P_ele excluding the outliers (326 sets), 3) data with P_cal including the outliers (330 sets), and 4) data with P_cal excluding the outliers (275 sets). Table 4 shows the averaged results from 10 iterations for the RMSE, MAE, and R² for the cases of “Train” and “Test”: “Train” represents the accuracy evaluation result for the test using training data (randomly selected 90 % of the data) and “Test” represents the accuracy evaluation result for the test using untraining data (remaining 10 % of the data) in K-fold cross validation. The MAE and RMSE values closer to 0 and a value of R² closer to 1 indicate a higher prediction performance [55], [56].

Table 4.

Evaluation of the performance of ML models for the rate constant prediction using the RMSE, MAE, and R² [“Train” represents the accuracy evaluation result for the test using training data (randomly selected 90% of the data) and “Test” represents the accuracy evaluation result for the test using untraining data (remaining 10% of the data) in K-fold cross validation.].

Evaluation of ML models		Data with Pele including the outliers	Data with Pele excluding the outliers	Data with Pcal including the outliers	Data with Pcal excluding the outliers
RF	RMSE (Train)	0.4265	0.0368	0.2185	0.0020
	MAE (Train)	0.1220	0.0742	0.0988	0.0187
	R2 (Train)	0.5937	0.9134	0.7791	0.9334
	RMSE (Test)	0.9679	0.2286	0.5358	0.0160
	MAE (Test)	0.3883	0.2740	0.2357	0.0744
	R2 (Test)	−0.2514	0.4041	−0.1461	0.4792
XGB	RMSE (Train)	0.4588	0.0505	0.0791	0.0019
	MAE (Train)	0.1683	0.1109	0.0686	0.0243
	R2 (Train)	0.5614	0.8811	0.9198	0.9360
	RMSE (Test)	0.9586	0.2144	0.5457	0.0160
	MAE (Test)	0.3487	0.2616	0.1813	0.0678
	R2 (Test)	−0.1954	0.4490	−2.4308	0.4709
LGB	RMSE (Train)	0.4231	0.0318	0.0020	0.0001
	MAE (Train)	0.1103	0.0559	0.0197	0.0052
	R2 (Train)	0.5975	0.9251	0.9979	0.9972
	RMSE (Test)	0.9688	0.2380	0.3436	0.0140
	MAE (Test)	0.3702	0.2892	0.1775	0.0665
	R2 (Test)	−0.2378	0.3414	0.2291	0.5357

Higher accuracy was obtained for the data with P_cal than those with P_ele, which indicated that the P_cal data might be more appropriate for quantitatively analyzing sonochemical activity and applying the ML algorithms. It should be noted that the P_ele data included the measured P_ele using a power meter, and the displayed (or provided by the manufacturer) P_ele on a device. Moreover, the results using data that excluded outliers showed higher accuracy because of the more focused ML effect for smaller scopes [42], [43], [44], [45]. However, this could significantly reduce diversity in the collected datasets and narrow the variable scope of the ML application. More datasets should be collected to reduce the outliers and appropriate outlier handling methods should be developed to ensure diversity in datasets [63], [64].

It was found that the evaluation metrics for the test using “Train” data resulted in higher accuracy than the test using “Test” data for RMSE, MAE, and R². This was because the trained ML model was tested on the data sets that it had already experienced for the cases of “Train”. On the other hand, the evaluation metrics for “Test” were obtained from the new data sets that the ML model had never experienced [65]. This indicates that ML methods might be somewhat vulnerable for less-trained or unseen data, which is why more related data should be accumulated over wider ranges for the potential use of ML. The results in Table 4 also indicated that relatively low accuracy for “Test” might represent the data in wide ranges for the variables collected in this study [66]. Among the three ML models, the XGB model showed the most reliable results, especially for the data with P_cal excluding the outliers. The difficulty of determining which ML model is more appropriate for handling collected data has previously been reported [19], [25], [30], [67].

3.3. Data augmentation

To improve the accuracy of ML performance, data augmentation has been widely utilized to address data scarcity in the image and natural language domains [68], [69], [70]. Data augmentation has been also used to increase the number of chemical structure datasets in chemistry [71], [72], [73], [74], [75], [76]. However, in the chemical and environmental engineering fields, its application in ML/DL has rarely been reported. Numerical data can be augmented using a Gaussian distribution, or by randomly generating new datasets of input variables from the original data [77]. However, data that are randomly generated or significantly different from the original data may result in low accuracy of the ML model, despite the use of more datasets. In this study, we suggested a novel noise injection method to increase the size of the training data. New datasets were generated by adding values ranging from ± 0.01 % to 10 % of the original dataset (data with P_cal excluding the outliers), which were used for the prediction of the rate constants in the ML models.

As shown in Fig. 3, the augmented data resulted in significantly higher accuracy for all applied models, and the smallest change in the original datasets (adding a value of 0.01 %) induced the most reliable ML performance in this study. This indicates that an increase in the number of datasets with a slight change in the variables could noticeably enhance the ML performance. However, it is not clear whether augmentation methods such as noise injection are statistically reliable because few ML results using data augmentation have been reported in the context of chemical and environmental engineering data.

Fig. 3.

Comparison of performance of ML models using the augmented data.

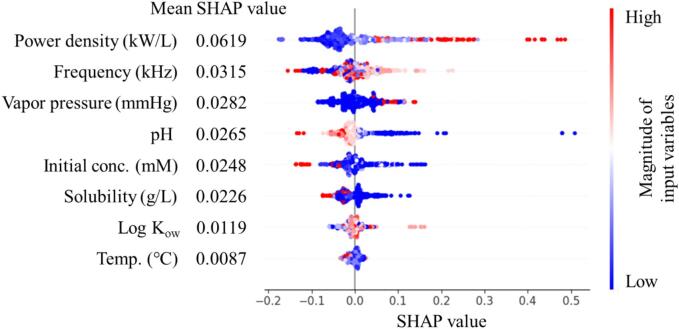
It has been known that ML models are barely understood intuitively and they are called as black-box models [57], [78]. To understand the contribution of each input variable to the predicted target values (rate constants in this study), the outcome of the trained ML method, the SHAP method, was applied to the aforementioned augmented data. In Fig. 4, the input variables are listed from top to bottom in the order in which they predominantly affect the ML predicted target value, and the most influential variables were the power density (Mean SHAP value: 0.0619) and frequency (Mean SHAP value: 0.0315) in this study. Vapor pressure, pH, initial conc., and solubility also made considerable contributions to the ML performance. In addition, more positive SHAP values of the input variables have a more positive impact on the predicted target values, whereas negative SHAP values have the opposite effect. Thus, the application of a high power density (positive SHAP values/red color and negative SHAP values/blue color), moderate frequency (positive SHAP values/white color and negative SHAP value/red and blue color), and low pH (positive SHAP values/blue color and negative SHAP values/red color) can result in high rate constants for sonochemical degradation. This result appeared somewhat consistent with previous sonochemistry results [79], [80] and further data accumulation was required to better understand the contribution of the input variables in the ML analysis.

Fig. 4.

Input variable contribution analysis on the target value (rate constants) using the SHAP method.

3.4. Application of trained ML model

The applicability of the trained ML models using augmented data was investigated to predict the pseudo-1st-order reaction kinetic constant for sonochemical degradation in the frequency range of 20–1,000 kHz. Fig. 5 shows the predicted results of the ML models for two pollutants, naphthol blue black and phenol, which were the most reported pollutants in our collected data. Other input variables, such as the power density, initial concentration, temperature, and pH, were determined as the median values of the collected datasets of the target pollutant (naphthol blue black or phenol), as shown in Fig. 5.

Higher rate constants were obtained in the frequency ranges of 100–600 and 400–500 kHz for naphthol blue black and phenol, respectively. As no significant trends in the rate constants were observed for the two pollutants, it was difficult to determine whether the predicted results were reliable. It is notable that the datasets of naphthol blue black (21 sets) were obtained from two papers from a single research group, indicating that limited experimental conditions were applied using frequencies of 585, 860, and 1140 kHz. Thus, the predicted results for the low-frequency range had relatively low accuracy. For phenol, datasets (23 sets) were obtained from eight papers by various research groups, indicating that a variety of experimental conditions and their results were trained in the ML models. The frequencies of the phenol datasets collected were 20, 30, 35, 200, 300, 500, 520, and 534 kHz. However, less training of the ML models under certain conditions may be conducted for phenol, despite the more varied frequency conditions. Consequently, it is recommended that more data over wider experimental conditions including ultrasound-based AOPs from different research groups be accumulated and analyzed to obtain more reliable predicted results using ML models.

4. Conclusion

In this study, novel ML models, including RF, XGB, and LGB, were used to predict pseudo-1st-order reaction rate constants for the sonochemical degradation of aqueous organic pollutants. A total of 618 sets of data, including ultrasonic, solution, and pollutant characteristics, were used for training the ML models. The ML models were well trained with high accuracy for the prediction of rate constants using data with P_cal excluding the outliers; the XGB model exhibited the highest performance among the applied models. Data augmentation can significantly enhance the accuracy of an ML model by increasing the size of the training data. However, the application of the trained ML model for the two selected pollutants in the frequency range of 20–1,000 kHz resulted in uncertain predictions. Additional data on a wider range of experimental conditions from different research groups are required for the use of ML models in sonochemistry.

CRediT authorship contribution statement

Iseul Na: Writing – review & editing, Writing – original draft, Validation, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Taeho Kim: Validation, Methodology, Investigation. Pengpeng Qiu: Methodology, Validation, Writing – review & editing. Younggyu Son: Writing – review & editing, Writing – original draft, Validation, Supervision, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: