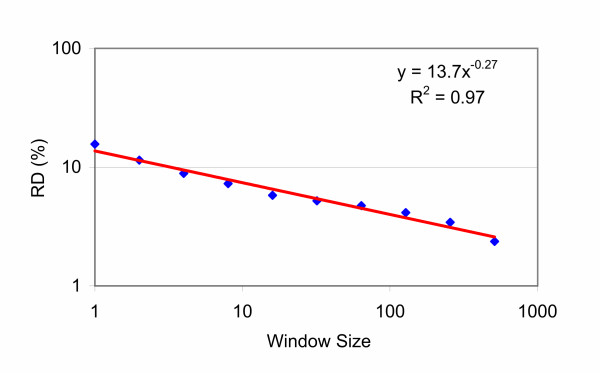
Figure 2.

Monofractal Analysis of the breathing pattern. Monofractal or residual dispersion (RD) analysis – one of a number of ways that fractal behaviour can be analysed [25]. RD is defined as standard deviation/mean × 100. This analysis uses data from Figure 1 with pooled data (or window sizes) based on powers of 2ⁿ following a log-log transform. A linear relationship indicates fractal behaviour, if the slope of the line lies between – 0.5 and 0. If these conditions are met the data fits an equation of the form y = 1/x^α defining a power law; with slope = α. The fractal dimension (D) is defined a 1 - α. D was 1.27 over 2.71 decades (log 512) with R² = 0.97. D of 1.0 defines a completely homogeneous data set, and 1.5 defines a completely random set (white noise). In between these two boundary conditions the data has fractal characteristics.