Figure 3.

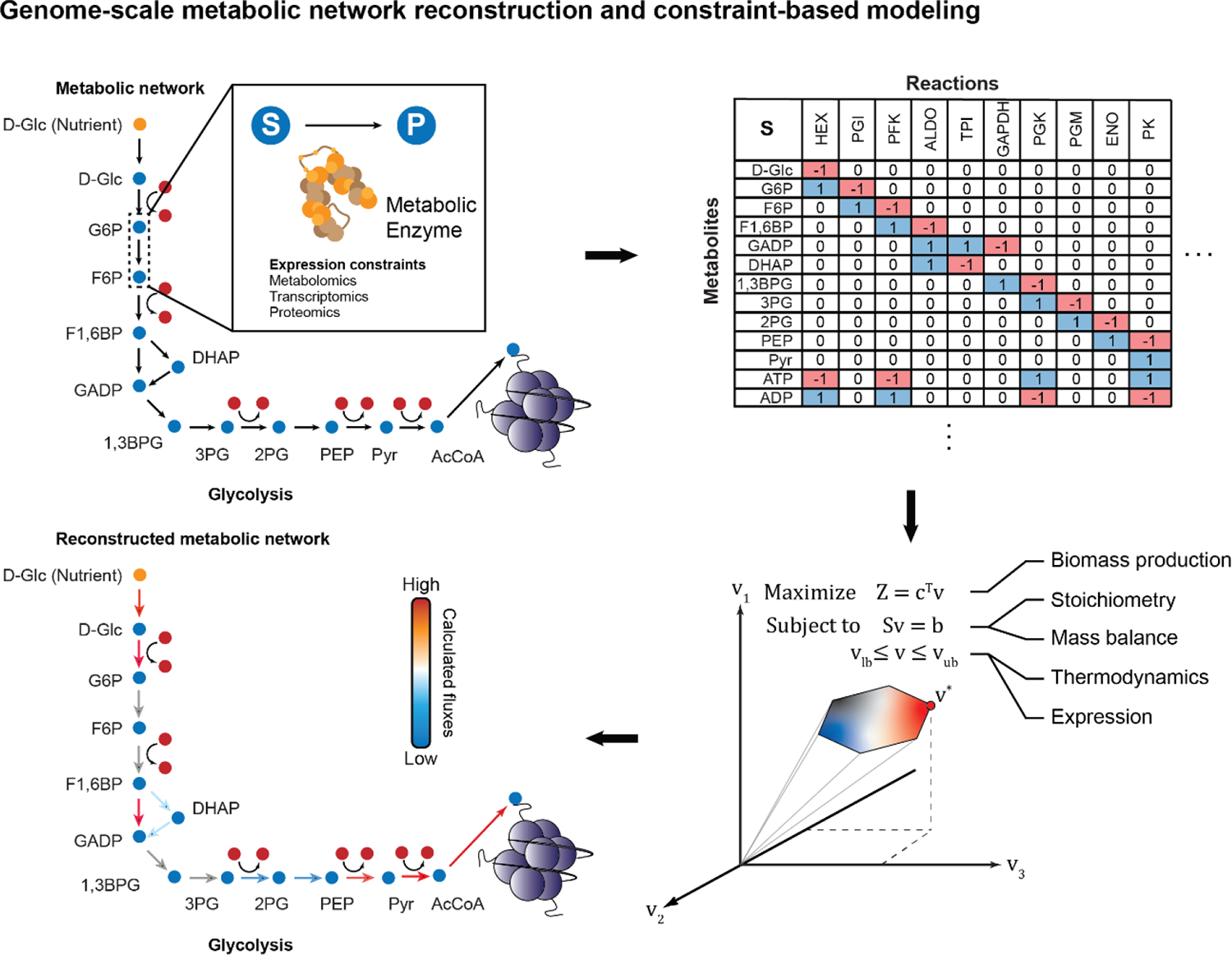
Using Constraint-based Modeling (CBM) to compute metabolic fluxes through the metabolic network. Genome-scale metabolic network reconstructions map all known gene-protein-reaction associations using an iterative process of literature curation, database mining, and model refinement. The resulting metabolic network is converted to a mathematical form as a matrix of the stoichiometries (S) for every single reaction-metabolite pair. The product of the stoichiometric matrix (S) and the desired vector of metabolic fluxes going through each reaction (v) is equal to the rate of change of metabolites (b). If b is set to 0, this represents quasi-steady state conditions. Solving for v provides steady-state fluxes from the metabolic reconstruction. To get a unique biologically feasible flux distribution, several constraints must be imposed on the model. A cellular objective is set, where a cell is assumed to fulfill a specific metabolic task such as maximizing biomass production. Further, the structure of the metabolic network itself (S), given that each reaction is mass- and charge-balanced, provides another constraint.