TABLE 2.

Characteristics of the best-fitting models^a

Model	Comparison group	Interaction term?	SHIV variant
			SHIV-KB9(−225)		SHIV-KB9(−305)
			F (df)	R2 (%)	F (df)	R2 (%)
Nonlinear exponential decayb	SHIV-KB9/SHIV-KB9ecto	No	51 (4, 37)	83	65 (4, 37)	86
		Yes	50 (5, 36)	86	66 (5, 36)	89
Inversec	SHIV-KB9/SHIV-KB9ecto	No	16 (3, 37)	54	15 (3, 37)	51
		Yes	23 (4, 36)	69	35 (4, 36)	77

^aThe relationship between cumulative antigenemia and the CD4⁺ T-lymphocyte set point in the SHIV-infected monkeys was analyzed using a nonlinear exponential decay model or an inverse model (23, 67). Each model was considered with or without a virus group-replication interaction term; the interaction term allowed the shapes of the curves to vary independently by virus group. The F statistic describes goodness of fit, and the adjusted R² value describes the proportion of variability explained by the model (23, 33). The degrees of freedom (df) for the F statistics are shown in parentheses. The F statistics and adjusted R² values for the comparisons of the SHIV-KB9(−225) and SHIV-KB9(−305) viruses with the SHIV-KB9/SHIV-KB9ecto group are shown for each model. 

^bThe formula for the nonlinear exponential decay model with interaction term is 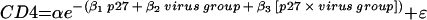, where CD4 is the CD4⁺ T-lymphocyte set point and p27 is the cumulative p27 antigenemia. 

^cThe formula for the inverse model with interaction term is CD4 = 1/(β₀ + β₁ p27 + β₂ virus group + β₃ [p27 × virus group]) + ɛ, where CD4 is the CD4⁺ T-lymphocyte set point and p27 is the cumulative p27 antigenemia.