Abstract
We introduce several improvements to the penalty-based variational quantum Monte Carlo (VMC) algorithm for computing electronic excited states of Entwistle et al. [Nat. Commun. 14, 274 (2023)] and demonstrate that the accuracy of the updated method is competitive with other available excited-state VMC approaches. A theoretical comparison of the computational aspects of these algorithms is presented, where several benefits of the penalty-based method are identified. Our main contributions include an automatic mechanism for tuning the scale of the penalty terms, an updated form of the overlap penalty with proven convergence properties, and a new term that penalizes the spin of the wave function, enabling the selective computation of states with a given spin. With these improvements, along with the use of the latest self-attention-based ansatz, the penalty-based method achieves a mean absolute error below 1 kcal/mol for the vertical excitation energies of a set of 26 atoms and molecules, without relying on variance matching schemes. Considering excited states along the dissociation of the carbon dimer, the accuracy of the penalty-based method is on par with that of natural-excited-state (NES) VMC, while also providing results for additional sections of the potential energy surface, which were inaccessible with the NES method. Additionally, the accuracy of the penalty-based method is improved for a conical intersection of ethylene, with the predicted angle of the intersection agreeing well with both NES-VMC and multireference configuration interaction.
1. Introduction
The central challenge toward an ab initio description of chemical processes is solving the electronic Schrödinger equation for molecules and materials. Its solutions provide, in principle, a full description of a system’s electronic properties, facilitating simulation from first principles. While many quantum chemistry methods target only electronic ground states, access to low-lying excited states is necessary for accurately modeling phenomena such as the interaction of light and matter or catalysis.1−5 Light-matter interactions are of utmost importance for many processes in photochemistry, such as photoisomerization in the retinal chromophore6 or photodissociation in photosynthesis.7 These photoinduced processes are notably at the core of several research frontiers, including the enhancement of light-harvesting materials for solar cells8,9 and the development of phototriggered drugs and medical screening devices.10,11
Despite the demand for accurate approximations of electronic excited states, their simulation remains challenging to this date.12−14 While density functional theory is the workhorse of many quantum chemistry simulations, its applicability to excited states is limited and its extensions, such as time-dependent density functional theory (TDDFT), have their well-known limitations.15−17 Single-reference coupled cluster theory can be extended to target excited states, but it fails to correctly describe bond breaking and struggles with degeneracies, requiring a costly multireference treatment.17 A commonly used alternative for the computation of excited states is the complete active space self-consistent field (CASSCF) algorithm. Although CASSCF has demonstrated considerable success, it scales exponentially with the size of the active space. Consequently, it relies heavily on a careful selection of active orbitals, often requiring chemical intuition and prior knowledge of the system under investigation.18 Furthermore, the choice of compatible active spaces across molecular geometries poses additional complications for modeling excited-state potential energy surfaces. As a consequence, the modeling of excited-state dynamics often involves substantial human intervention, relying heavily on chemical intuition and a trial-and-error approach.
Variational quantum Monte Carlo (VMC) provides a promising alternative to the established protocols. In recent years the introduction of neural-network wave functions has significantly enhanced the accuracy of VMC.19,20 The application of neural-network wave functions for the VMC simulation of molecular systems has proven highly successful in accurately describing states with multireference character and modeling strong correlation.21 Recently, these methods have been successfully extended to enable simulations of excited states22 via a penalty-based formalism. While results on some applications have already been promising, the methodology for simulation of excited states with neural-network based VMC is still under active development.23−26 In this work, we introduce advancements in penalty-based VMC for excited states and conduct a comparative analysis of our approach with alternative methods, such as the recently proposed natural excited state quantum Monte Carlo (NES-VMC),24 a sequential variant of the penalty-based method,23 as well as the auxiliary wave function approach of Lu and Fu (AW).26
Our main contribution is the greatly improved accuracy of the penalty-based method for excited states, due to improvements in the optimization and the use of the more expressive self-attention-based Psiformer wave function architecture.27 The methodological improvements include the alteration of the loss function of Entwistle et al.22 to a form with proven convergence properties,25 and automatically tuning the scale of the penalty term to reduce noise in the gradients, while retaining the global minimum of the loss function and preventing the collapse of the states. We utilize the KFAC optimizer28 and tune its hyperparameters to account for the number of model parameters increasing with the number of excited states. Furthermore, we introduce a method to target states with a specific spin by combining the selection of the magnetic quantum number of the spin-assigned wave function with a spin penalty that favors low-spin states. This approach enhances the efficiency of computing excited states by segmenting them into spin sectors and enables precise targeting of desired spin states. The method is combined with the use of pseudo potentials,29,30 which we employ for heavy atoms (second row and beyond) throughout this work. We present results for our improved method on a variety of atomic and molecular systems ranging from 4 to 42 electrons. The first set of experiments focuses on single-point calculations, demonstrating high accuracy on the ten lowest-lying states of first- and third-row atoms, as well as on the five lowest-lying states of a variety of organic and inorganic molecules. In order to validate the accuracy of our wave functions, we compute the oscillator strengths of ground- to excited-state transitions in the molecules. The second part of the experiments targets excited-state potential energy surfaces, where we model the intricate electronic structure of the carbon dimer and the conical intersection of ethylene. For the carbon dimer, we recover a large fraction of the potential energy surface for a total of nine states, composed of four singlet, four triplet and a quintet state. For the ethylene isomerization process, we improve over previous calculations with penalty-based excited-state VMC and predict the pyramidalization angle of the conical intersection in good agreement with the NES-VMC method.
2. Methods
The aim of wave function-based electronic structure methods is to approximate the solution to the time-independent electronic Schrödinger equation:
| 1 |
where 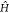 is the electronic Hamiltonian with eigenstates
is the electronic Hamiltonian with eigenstates 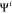 and corresponding energies Ei, with the states conventionally ordered
according to increasing energy. For molecular systems in the Born–Oppenheimer
approximation and using atomic units,
and corresponding energies Ei, with the states conventionally ordered
according to increasing energy. For molecular systems in the Born–Oppenheimer
approximation and using atomic units, 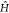 takes the form
takes the form
| 2 |
with ZI being the nuclear
charges, while 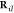 and
and 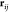 denote electron–nucleus and electron–electron
distances, respectively. As the electronic Hamiltonian is Hermitian,
all Ei are real and
denote electron–nucleus and electron–electron
distances, respectively. As the electronic Hamiltonian is Hermitian,
all Ei are real and 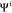 are orthogonal to each
other. Furthermore,
we assume all
are orthogonal to each
other. Furthermore,
we assume all 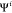 to be real-valued which
can always be ensured
for molecular wave functions. Ground-state electronic structure approaches
are concerned by computing only the lowest energy E0, and corresponding ground-state wave function Ψ0 of a given system. The objective of excited state methods
extends to computing the lowest n energies along
with their corresponding states for the system under consideration.
to be real-valued which
can always be ensured
for molecular wave functions. Ground-state electronic structure approaches
are concerned by computing only the lowest energy E0, and corresponding ground-state wave function Ψ0 of a given system. The objective of excited state methods
extends to computing the lowest n energies along
with their corresponding states for the system under consideration.
2.1. Variational Optimization
2.1.1. Variational Monte Carlo
Variational quantum Monte Carlo (VMC) belongs to the family of variational methods for approximating the eigenstates of a quantum many-body system. These methods are based on the variational principle of quantum mechanics, which states that the functional given by the expectation value of the Hamiltonian
| 3 |
is minimized for the (unnormalized) ground-state
wave function Ψ0. This Rayleigh quotient can be understood
as a loss function for optimization of a parametrized ansatz 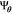 :
:
| 4 |
where θ are the model parameters
and the optimal parameters 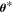 are to be found. A challenging
aspect of
this optimization is the computation of integrals over the high-dimensional
domain of the wave function. VMC solves this problem by numerically
approximating integrals, such as the computation of the expectation
value of observable
are to be found. A challenging
aspect of
this optimization is the computation of integrals over the high-dimensional
domain of the wave function. VMC solves this problem by numerically
approximating integrals, such as the computation of the expectation
value of observable 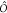 , through
Monte Carlo integration:
, through
Monte Carlo integration:
| 5 |
outlining an algorithm that poses very few
restrictions on the form of ansatz parametrization. Minimizing Monte
Carlo estimates of the objective function amounts to an alternating
scheme of sampling electron positions 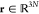 from the
probability density associated
with the square modulus of the wave function
from the
probability density associated
with the square modulus of the wave function 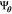 and updating the model parameters θ with a variant of stochastic gradient descent. Note
that for the electronic Hamiltonian it is convenient to work with
the spin-assigned real-valued wave function
and updating the model parameters θ with a variant of stochastic gradient descent. Note
that for the electronic Hamiltonian it is convenient to work with
the spin-assigned real-valued wave function 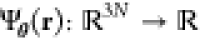 . For a detailed description of the VMC
method with application to neural-network wave functions see the work
of Schätzle et al.31
. For a detailed description of the VMC
method with application to neural-network wave functions see the work
of Schätzle et al.31
2.1.2. Optimizing Excited States with the Overlap Penalty
The variational method can be extended to excited
states by accounting for the orthogonality of the eigenstates. The
relevant partition of the spectrum of the Hamiltonian can be constructed
by finding the orthogonal subspace with minimal energy. A conceptually
simple way of approximating the n lowest eigenstates 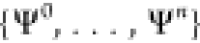 of a system is to impose their orthogonality
by extending the objective function with an overlap penalty:
of a system is to impose their orthogonality
by extending the objective function with an overlap penalty:
| 6 |
resulting in the coupled optimization
of multiple ansatzes. The global minimum of this objective function
is attained for the lowest-lying states, if αij is chosen to be larger than the energy gap between the ith and jth state.25 The overlap between each pair of (unnormalized) states can again
be computed by Monte Carlo integration.22 To enforce pure eigenstates and increase the training stability,
we apply the orthogonality constraint only with respect to lower-lying
states, resulting in a total of n(n − 1)/2 relevant overlap terms, for n states.
To achieve this, the gradients of the overlap term are computed only
with respect to  by detaching
by detaching  from the computational
graph. Note that
in contrast to the above construction, a loss function with symmetric
overlap penalty terms yielding gradients to both the lower and higher
lying states would be minimized by all linear combinations of the
lowest n states. While Entwistle et al.22 used a variant of the loss function that diverges
upon the collapse of two eigenstates, increasing training stability
at the cost of a small bias in the excitation energies, our improved
method is unbiased, and stable using the simpler penalty term introduced
by Pathak et al.32 Recently Wheeler et
al.25 have introduced an ensemble method,
where the presented loss function can be derived in a more general
framework.
from the computational
graph. Note that
in contrast to the above construction, a loss function with symmetric
overlap penalty terms yielding gradients to both the lower and higher
lying states would be minimized by all linear combinations of the
lowest n states. While Entwistle et al.22 used a variant of the loss function that diverges
upon the collapse of two eigenstates, increasing training stability
at the cost of a small bias in the excitation energies, our improved
method is unbiased, and stable using the simpler penalty term introduced
by Pathak et al.32 Recently Wheeler et
al.25 have introduced an ensemble method,
where the presented loss function can be derived in a more general
framework.
2.1.3. Targeting Spin States with Spin Penalty
In many applications, selection rules prohibit excitations that would involve changing the spin of the electronic state. Consequently, states within a fixed spin sector are often of interest. While states of the targeted spin sector can be selected from a simulation of all low-lying eigenstates through evaluation of the spin of the acquired wave functions, this procedure potentially involves the computation of many ultimately irrelevant states. A common approach to address this issue is to offset states based on their spin, pushing them out of the targeted region of the spectrum. We employ a similar technique in the context of VMC by augmenting our loss function with a spin penalty:
| 7 |
where 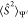 is the expectation value of the squared
magnitude of the spin operator and β weighs the penalty term.
The expectation value of the spin operator is evaluated through Monte
Carlo sampling, as described in Section 2.5. As the molecular Hamiltonian commutes
with the spin operator, they share a common set of eigenstates. This
makes pure spin states a valid target of the variational optimization
and evaluation of the spin expectation value with Monte Carlo integration
efficient. For sufficiently large β, this objective function
favors solutions with low total spin, that is singlet (doublet) states
for systems with an even (odd) number of electrons. In order to obtain
higher spin states, i.e., triplet (quartet) states, we fix the mS component of our ansatz accordingly.
We again include the spin penalty, now yielding the solution minimizing
the total spin magnitude within the subset of constrained wave functions.
Although the restriction to the subspace of higher spin states by
fixing the difference between spin-up and spin-down electrons has
been previously discussed in the context of penalty-based excited
state optimization,23 the integration of
the spin penalty enables us to leverage this concept to target states
with specific spins. For a detailed explanation of the treatment of
spin in VMC wave functions, see Section S3. Note that while minimizing the total spin of the wave function
allows for reformulating the gradients to contain only first derivatives,22 this is no longer possible when targeting a
specific value of the spin expectation through the minimization of
the difference from that targeted value. Furthermore, we highlight
that the aforementioned penalty approach can be extended to restrict
VMC ansatzes based on other observable quantities. For example, it
is possible to penalize or favor states of a certain spacial symmetry
or target other properties of the eigenstates if their operators commute
with the Hamiltonian.
is the expectation value of the squared
magnitude of the spin operator and β weighs the penalty term.
The expectation value of the spin operator is evaluated through Monte
Carlo sampling, as described in Section 2.5. As the molecular Hamiltonian commutes
with the spin operator, they share a common set of eigenstates. This
makes pure spin states a valid target of the variational optimization
and evaluation of the spin expectation value with Monte Carlo integration
efficient. For sufficiently large β, this objective function
favors solutions with low total spin, that is singlet (doublet) states
for systems with an even (odd) number of electrons. In order to obtain
higher spin states, i.e., triplet (quartet) states, we fix the mS component of our ansatz accordingly.
We again include the spin penalty, now yielding the solution minimizing
the total spin magnitude within the subset of constrained wave functions.
Although the restriction to the subspace of higher spin states by
fixing the difference between spin-up and spin-down electrons has
been previously discussed in the context of penalty-based excited
state optimization,23 the integration of
the spin penalty enables us to leverage this concept to target states
with specific spins. For a detailed explanation of the treatment of
spin in VMC wave functions, see Section S3. Note that while minimizing the total spin of the wave function
allows for reformulating the gradients to contain only first derivatives,22 this is no longer possible when targeting a
specific value of the spin expectation through the minimization of
the difference from that targeted value. Furthermore, we highlight
that the aforementioned penalty approach can be extended to restrict
VMC ansatzes based on other observable quantities. For example, it
is possible to penalize or favor states of a certain spacial symmetry
or target other properties of the eigenstates if their operators commute
with the Hamiltonian.
2.2. Comparison with Other VMC Methods for Excited States
While the field of VMC for molecules in first quantization using neural-network wave functions has mostly settled on the optimal strategy for ground-state optimization, the methodology of excited-state optimization is still subject to ongoing development. In this section, we compare the penalty-based method with other available strategies and point out some of their respective advantages and disadvantages.
The most recent alternative to penalty-based VMC for excited states is the natural-excited-state VMC (NES-VMC) approach of Pfau et al.24 In NES-VMC, the problem of finding the lowest n eigenstates of the physical Hamiltonian is transformed to finding the ground state of the Hamiltonian of an extended system with n times as many electrons. Unlike penalty-based approaches, this elegant formulation allows trial wave functions to be optimized to match a linear combination of the lowest excited states without imposing additional constraints. The main drawback of NES-VMC lies in the necessity to model and sample an extended system of electrons. The larger effective system size increases computational costs in two ways. First, it requires the evaluation of much larger determinants, which constitutes the step with the steepest theoretical scaling in the whole deep-learning VMC algorithm. Second, wave functions of the extended system form a higher dimensional Hilbert-space than those of the physical system, leading to a quicker onset of the “curse of dimensionality”. On top of the increased computational costs, NES-VMC requires an additional diagonalization of the local energy matrix to recover the energies and wave functions of the individual states from the solution of the extended system. This also means that one does not have access to the energies and other properties of the states throughout optimization, making the convergence of individual states difficult to measure without incurring further computational costs for frequent diagonalizations. A small additional drawback of the coupled nature of the states in NES-VMC is the requirement for heuristics to prevent numerical instabilities when states become nearly linearly dependent. Lastly, unlike in penalty-based VMC, there is no straightforward way to impose restrictions on the spin of the ansatzes. This limitation may require the simulation of other, irrelevant, lower-lying states, simply to access the higher-lying states of interest.
Next, the sequential variant of the penalty-based method for excited states recently proposed by Liu et al.23 is considered. In this approach, a simple ground-state computation is carried out to convergence before running a second calculation for the first excited state. The second calculation incorporates an overlap penalty term with respect to the fixed ground state obtained from the first calculation. The process is then repeated for higher-lying excited states, with a growing number of penalty terms applied to all previously obtained wave functions. While this strategy might help stabilize the early steps of training and potentially enable access to higher-lying states when optimizing numerous ansatzes in parallel is prohibitively expensive, its sequential nature makes it difficult to use in practice. Most importantly, one only receives feedback on the quality of the highest state after completing the computations for all preceding states. This could result in a significant amount of repeated computation compared to regular penalty-based VMC, where the quality of all states can be assessed from the earliest stages, allowing for early adjustments. Additionally, the necessity to fully converge all computations for the lower-lying states before starting the next calculation means there is no flexibility to stop the training early if relative energies have converged, or to continue training if the desired accuracy has not yet been achieved, without breaking the sequential paradigm.
Another closely related alternative is the auxiliary wave function method of Lu and Fu.26 This method avoids the dependence on a free parameter to scale the overlap penalty by combining the orthogonalization of Choo et al.33 with the real-space overlap computations used by Entwistle et al.22 In this method, excited states are found by running sequential optimizations where previously converged lower-lying states are projected out from the currently optimized ansatz. To achieve this, overlaps between the current wave function and all lower-lying wave functions are computed, allowing the energy contributions from the n – 1 lower-lying states to be subtracted, to obtain the energy expectation value of the nth excited state. While this method eliminates the hyperparameter used for weighting the overlap penalty, it does so at the cost of retaining only an implicit representation of the excited-state wave functions, while still requiring the computation of the same overlap terms as in the penalty-based method. Additionally, the computation of observables necessitates evaluating all pairwise overlaps with respect to each lower-lying state, leading to significantly higher computational costs and making the targeting of specific spin states infeasible. Furthermore, stochastic errors in the difficult-to-estimate overlap terms affect the evaluation of observables more directly than in penalty-based VMC. Lastly, Lu and Fu demonstrated that their results can be reproduced with penalty-based methods, incurring slightly lower computational costs, if the overlap penalty is weighted correctly. This task is facilitated by the automatic penalty scaling introduced in this work.
Finally, we consider the method of targeting excited states via variance minimization.34,35 This approach minimizes the variance of the local energies of each state, leveraging the fact that this variance should be zero for all eigenstates of the Hamiltonian. The method relies on sufficiently accurate initial guesses to ensure convergence to the desired states. Cuzzocrea et al.36 demonstrated that for increasingly complex Slater–Jastrow type ansatzes, the variance minimization scheme becomes prone to escape the local minima of the target state, and often converges to other states with lower variance. A further complication of variance minimization with neural-network ansatzes is the appearance of mixed third derivatives of the wave function in the gradient expression of the loss function. Due to the large number of ansatz parameters, these quantities significantly increase the computational cost of the gradient calculation, which already forms one of the bottlenecks of the algorithm. Variance minimization has therefore not been often employed in the recent neural-network-based VMC approaches to excited states.
2.3. Neural-Network Wave Function Ansatz
Neural-network-based wave function ansatzes have been very successful in describing intricate many-body correlation in quantum systems.21 The state-of-the-art architectures for molecules in first quantization are implemented via the concept of linear combinations of generalized Slater determinants:
| 8 |
employing the determinant as an antisymmetrizer over permutation equivariant many-body orbitals:
| 9 |
The expressivity
of the wave functions arises
from the parametrization of 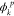 as neural
networks, while the envelope
functions
as neural
networks, while the envelope
functions 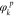 implement
the correct asymptotics. The
major difference between the existing architectures is how the latent-space
representation of the electrons, ultimately projected to obtain the
many-body orbitals
implement
the correct asymptotics. The
major difference between the existing architectures is how the latent-space
representation of the electrons, ultimately projected to obtain the
many-body orbitals 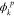 , is
constructed from the electron and nuclear
positions. The experiments throughout this work are performed with
the Psiformer architecture.27 The Psiformer
electron embeddings h are instantiated based on the (scaled)
electron nuclei distances and their respective spin. Electronic correlation
is then built up incrementally through subsequent self-attention interactions,
resembling the encoder part of a transformer:
, is
constructed from the electron and nuclear
positions. The experiments throughout this work are performed with
the Psiformer architecture.27 The Psiformer
electron embeddings h are instantiated based on the (scaled)
electron nuclei distances and their respective spin. Electronic correlation
is then built up incrementally through subsequent self-attention interactions,
resembling the encoder part of a transformer:
| 10 |
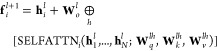 |
11 |
where SELFATTN
is the standard multiheaded
self-attention block,37 ⊕h denotes the concatenation over attention heads h, i indexes electrons and l indexes the layer. The subscripts q, v, k stand
for queries, values and keys, respectively and W and b are the weights and biases of the Psiformer layer. An electron-wise
linear projection on vectors of dimension 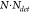 is applied to transform the output of the
last layer to the orbitals
is applied to transform the output of the
last layer to the orbitals 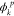 . Additionally,
the electronic cusps are
modeled with a multiplicative Jastrow factor:
. Additionally,
the electronic cusps are
modeled with a multiplicative Jastrow factor:
| 12 |
The Psiformer is implemented in the DeepQMC program package.38 For more information on the Psiformer we refer to the original publication of von Glehn et al.,27 while further details about the implementation of neural-network wave functions in DeepQMC can be found in Schätzle et al.31 Lastly, we emphasize that the penalty-based method for computing excited states can be applied in combination with any other valid ansatz architecture as well.
2.4. Pretraining and CASSCF Baseline
It is well-known20,31 that molecular ground-state VMC calculations employing neural-network ansatzes greatly benefit from a short supervised pretraining phase preceding the variational optimization. In this stage, a mean squared error loss function between the many-body orbitals of the ansatz and the single-particle orbitals of a reference HF or CASSCF solution is minimized:
| 13 |
where 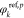 are the orbitals of the reference solution
with p enumerating determinants and k the respective orbitals. This pretraining serves as an informed
initialization scheme for the parameters of the neural network, and
can help in avoiding convergence to local minima, along with reducing
the number of expensive variational optimization steps necessary to
achieve a certain threshold of accuracy.
are the orbitals of the reference solution
with p enumerating determinants and k the respective orbitals. This pretraining serves as an informed
initialization scheme for the parameters of the neural network, and
can help in avoiding convergence to local minima, along with reducing
the number of expensive variational optimization steps necessary to
achieve a certain threshold of accuracy.
In the context of excited-state calculations, one can use the lowest n roots of a multistate CASSCF calculation as a pretraining target. Care must be taken during the definition of the active space,22 such that the resulting Slater-determinants of the CASSCF solution have the right spin configurations, and contain the necessary orbitals to describe all excitations of interest. The latter is of special importance when a great number of excited states of the smallest systems are considered, such as for the lithium atom in Section 3.2.1. In the case of the lithium atom, the lowest states can all be described as excitations of the single valence electron to higher and higher orbitals. To qualitatively describe the lowest n states, one must include at least n orbitals in the active space, which in turn might necessitate the use of single particle basis sets larger than the ones usually employed in deep-learning VMC pretraining targets. In the present work, the relatively large aug-cc-pVTZ39−41 basis set is used for most systems to ensure a quantitatively correct initialization of the highest excited states considered. The only exception is benzene, where the cc-pVDZ basis set41 is used instead, as the CASSCF computation with the aug-cc-pVTZ basis set is deemed too expensive, and where there is no need for diffuse basis functions. When targeting states with a specific spin, this has to be reflected in the calculation of the CASSCF baseline by restricting to the selected spin sector. The number of pretraining iterations is set to 1000 for all systems except for benzene, where 100 000 pretraining iterations were used, to make the variational training as efficient as possible.27 All CASSCF calculations have been performed with the PySCF program package.42 Minimal active spaces are chosen for all systems in the present study, selected by searching for the smallest active spaces that still produce sensible excitation energies with respect to the reference values. While these calculations give a qualitatively valid picture of the excitation energies, they are far from the quantitative accuracy of the deep-learning VMC simulations. For example, the mean absolute error of the excitation energies predicted by the baseline CASSCF calculations for the atoms and molecules considered in Section 3.2 is 350 meV (8 kcal/mol).
2.5. Evaluating Observables
In quantum mechanics, the wave function gives a complete description of the state of the system. Having access to the electronic wave function of molecules grants theoretical access to all their observable electronic properties. To extract these properties from our wave function models, Monte Carlo integration is employed. For single state properties eq 5 can be applied directly. For off-diagonal properties between unnormalized states, such as the overlap or the transition dipole moment, we follow Entwistle et al.22 and evaluate the geometric mean of the Monte Carlo estimates with respect to either of the two wave functions. In the following, we sketch out the evaluation of the expectation values of the total spin magnitude and the oscillator strength operators.
2.5.1. Spin Magnitude
The total spin magnitude of the spin-assigned wave function manifests in the symmetries of its spatial part (see Section S3). It can therefore be obtained from the spin-assigned wave function, by evaluating its symmetry properties under exchanges of opposite-spin particles.43 We follow the procedure employed in NES-VMC,24 and evaluate the spin as
| 14 |
where 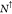 (
(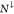 ) denotes the number of
spin-up (spin-down)
electrons, respectively. While the evaluation of the spin scales with
) denotes the number of
spin-up (spin-down)
electrons, respectively. While the evaluation of the spin scales with 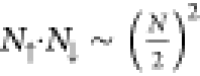 , it does not
involve the computation of
the local energy and is therefore of negligible cost for the systems
of the present study.
, it does not
involve the computation of
the local energy and is therefore of negligible cost for the systems
of the present study.
2.5.2. Transition Dipole Moment and Oscillator Strength
The oscillator strength is a useful quantity to
approximate the rate of transitions between electronic states as a
result of interaction with light, under the constant electric field
and dipole moment assumptions. Previous studies on neural-network-based
VMC for excited states have used the accuracy of the predicted oscillator
strength as a proxy to assess the quality of the underlying wave function
models.22,24 This is motivated by the fact that the oscillator
strength is highly dependent on the quality of the wave function approximation
and thus provides a useful measure for the accuracy of the wave function
on top of the energy. The oscillator strength fij is a dimensionless quantity obtained from
the energy gap ΔEij and the absolute value of the transition dipole moment defined as
the expectation of the dipole operator 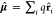 between states i and j:
between states i and j:
| 15 |
In practice, the off-diagonal expectation value of the dipole operator is evaluated using reweighted samples from the wave functions, and the excitation energy ΔEij is obtained by independently evaluating the energy expectation values of the two states.
2.6. Implementation Details
This section
describes the most important technical details of the penalty-based
method as implemented in the DeepQMC program package.31 In DeepQMC, the conventional deep-learning-based
ansatzes used for ground-state calculations are conveniently extended
to model a range of electronic states via the JAX framework’s44 vectorizing map function transformation. Using
this transformation, the 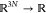 ansatz functions parametrized
by a single
set of parameters θ become functions
ansatz functions parametrized
by a single
set of parameters θ become functions 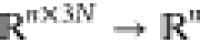 parametrized by n sets
of parameters
parametrized by n sets
of parameters 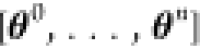 . In combination with the excited-state
loss function of (7), these extended ansatzes can then be used in
the existing deep-learning VMC framework of DeepQMC, with
a few minor modifications detailed below. To obtain the n sets of electron configuration samples in parallel, the same vectorizing
map transformation is used on the singe-state Markov-chain Monte Carlo
sampling routines. The hyperparameters of the KFAC optimizer28 used during the variational training are adjusted
as follows. Since an ansatz that describes n electronic
states is parametrized by n times as many parameters
as a single-state ansatz, the squared norm of a parameter update will
on average be n times larger as well (
. In combination with the excited-state
loss function of (7), these extended ansatzes can then be used in
the existing deep-learning VMC framework of DeepQMC, with
a few minor modifications detailed below. To obtain the n sets of electron configuration samples in parallel, the same vectorizing
map transformation is used on the singe-state Markov-chain Monte Carlo
sampling routines. The hyperparameters of the KFAC optimizer28 used during the variational training are adjusted
as follows. Since an ansatz that describes n electronic
states is parametrized by n times as many parameters
as a single-state ansatz, the squared norm of a parameter update will
on average be n times larger as well (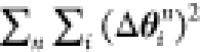 compared to
compared to 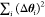 ). Accordingly, the KFAC
hyperparameter
controlling the maximum squared norm of parameter updates is scaled
by the number of computed states, n. The effect of
this change is most pronounced on the largest considered systems,
such as benzene, where the larger absolute values of total energies
can yield gradients with larger magnitudes, while on most of the smaller
systems investigated here the effect is not noticeable.
). Accordingly, the KFAC
hyperparameter
controlling the maximum squared norm of parameter updates is scaled
by the number of computed states, n. The effect of
this change is most pronounced on the largest considered systems,
such as benzene, where the larger absolute values of total energies
can yield gradients with larger magnitudes, while on most of the smaller
systems investigated here the effect is not noticeable.
Lastly, the treatment of the free parameters αij deserves some attention. As demonstrated by Pathak et al.,32 and later refined by Wheeler et al.25 these hyperparameters can be chosen freely without affecting the global minimum of the loss function, as long as
| 16 |
Furthermore,
we’ve found that while
all αij values satisfying (16) avoid
the collapse of the optimized states, values closer to the 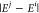 limit
can in some cases reduce the noisiness
of the training. Unfortunately, choosing the optimal value for αij while satisfying the above constraint can
require system-dependent manual tuning of these parameters. To alleviate
this issue, the automatic scaling of the αij parameters based on running estimates of Ei and Ej is introduced. In particular, the scaling of the
overlap penalty between states i and j is computed in each training step as
limit
can in some cases reduce the noisiness
of the training. Unfortunately, choosing the optimal value for αij while satisfying the above constraint can
require system-dependent manual tuning of these parameters. To alleviate
this issue, the automatic scaling of the αij parameters based on running estimates of Ei and Ej is introduced. In particular, the scaling of the
overlap penalty between states i and j is computed in each training step as
| 17 |
where 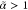 is the new free parameter shared between
all pairs of states,
is the new free parameter shared between
all pairs of states, 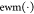 denotes
the exponentially weighted mean
over the training iterations, Eloc is
the batch of local energies in the current step, overbar denotes the
mean, and
denotes
the exponentially weighted mean
over the training iterations, Eloc is
the batch of local energies in the current step, overbar denotes the
mean, and 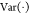 the variance.
The first argument of the
maximum function ensures that the constraint (16) is fulfilled while
automatically scaling αij in a system-specific
way, while the second argument prevents the collapse of the states
in the earliest stages of the training where
the variance.
The first argument of the
maximum function ensures that the constraint (16) is fulfilled while
automatically scaling αij in a system-specific
way, while the second argument prevents the collapse of the states
in the earliest stages of the training where 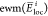 is not yet a good estimate
of Ei. As a result of
this parametrization,
the optimal value for the new parameter α̃ is significantly
less system-dependent than that of αij. For the bulk of the systems considered here, α̃
is set to four to ensure a comfortable margin of safety in satisfying
(16), while for a handful of systems it is decreased to two and one
to ensure optimal convergence in all cases. For concrete values of
α̃ employed for each system, see the Supporting Information. It is recognized that reducing the
dependence on the value of the α̃ parameter warrants further
research. On the other hand, considering the already limited range
in which the parameter is varied, along with the numerous benefits
of the method compared to other excited-state VMC approaches (detailed
in Section 2.2),
the penalty-based method can already be considered relevant, accurate,
and easy-to-apply in practice.
is not yet a good estimate
of Ei. As a result of
this parametrization,
the optimal value for the new parameter α̃ is significantly
less system-dependent than that of αij. For the bulk of the systems considered here, α̃
is set to four to ensure a comfortable margin of safety in satisfying
(16), while for a handful of systems it is decreased to two and one
to ensure optimal convergence in all cases. For concrete values of
α̃ employed for each system, see the Supporting Information. It is recognized that reducing the
dependence on the value of the α̃ parameter warrants further
research. On the other hand, considering the already limited range
in which the parameter is varied, along with the numerous benefits
of the method compared to other excited-state VMC approaches (detailed
in Section 2.2),
the penalty-based method can already be considered relevant, accurate,
and easy-to-apply in practice.
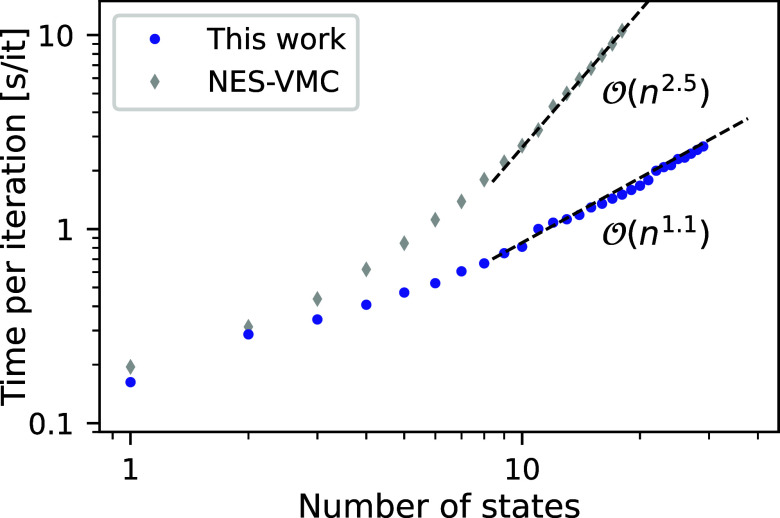
2.7. Scaling
The two dominant factors
determining the cost of any excited-state VMC computation are the
size of the considered physical system, and the number of computed
electronic states. A clear advantage of the penalty-based method over
extended-system approaches such as NES-VMC is that these two axes
of scaling are almost entirely decoupled from each other. In the NES-VMC
method, increasing the system size and considering more electronic
states both increase the number of simulated Fermions, bringing with
it the usual difficulties including reduced sampling efficiency, the
need to compute determinants of larger matrices, and the worsening
of the “curse of dimensionality”. In contrast, considering
new electronic states in penalty-based VMC only adds Fermions that
are simulated almost independently from the ones already present,
interacting with them only through the overlap penalty term of (7). In fact, the computation of this overlap term
is the only part of the algorithm that scales quadratically with the
number of electronic states, while the time complexity and memory
requirement of all other steps scale linearly. Fortunately, the cost
of the overlap computation is much smaller than that of the local
energies, when considering 1–30 electronic states, and therefore
the penalty-based method exhibits very favorable scaling in this regime,
as demonstrated in Figure 1. The points on this plot are obtained by performing a small
number of training iterations for the neon atom using an electron
configuration batch size of 64, while varying the number of computed
states. To reduce noise each experiment has been averaged over three
repetitions. With ten states or more, one finds an empirical scaling
of roughly 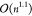 , indicating a practically linear scaling
of the penalty-based method with the number of electronic states.
Considering the NES-VMC results on the same system, one finds a much
steeper approximate scaling of
, indicating a practically linear scaling
of the penalty-based method with the number of electronic states.
Considering the NES-VMC results on the same system, one finds a much
steeper approximate scaling of 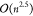 which is, as expected, similar to the scaling
of ground-state deep-learning VMC methods with the number of electrons.31 This steep scaling results in the fact that
while a single state iteration takes roughly the same time with the
NES-VMC code,45 an iteration with ten states
already takes four times as long. Lastly, we note that when during
inference with the penalty-bassed method, one is interested in the
properties of only a subset of the states (e.g the highest-lying states
only), one is free to decouple the optimized ansatzes, and evaluate
expectation values only for the selected states. This can help avoiding
unnecessary computation compared to the NES-VMC method, where the
ansatzes of the different states are only meaningful as a single unit,
and cannot be easily decoupled from each other.
which is, as expected, similar to the scaling
of ground-state deep-learning VMC methods with the number of electrons.31 This steep scaling results in the fact that
while a single state iteration takes roughly the same time with the
NES-VMC code,45 an iteration with ten states
already takes four times as long. Lastly, we note that when during
inference with the penalty-bassed method, one is interested in the
properties of only a subset of the states (e.g the highest-lying states
only), one is free to decouple the optimized ansatzes, and evaluate
expectation values only for the selected states. This can help avoiding
unnecessary computation compared to the NES-VMC method, where the
ansatzes of the different states are only meaningful as a single unit,
and cannot be easily decoupled from each other.
Figure 1.
Scaling of the computational
cost with the number of states. The
wall-clock time of a single training iteration is shown for the neon
atom, with an electron configuration batch size of 64 on a single
A100 GPU. Dashed lines represent least-squares fits to the penalty-based
and NES-VMC results with 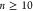 .
.
3. Results
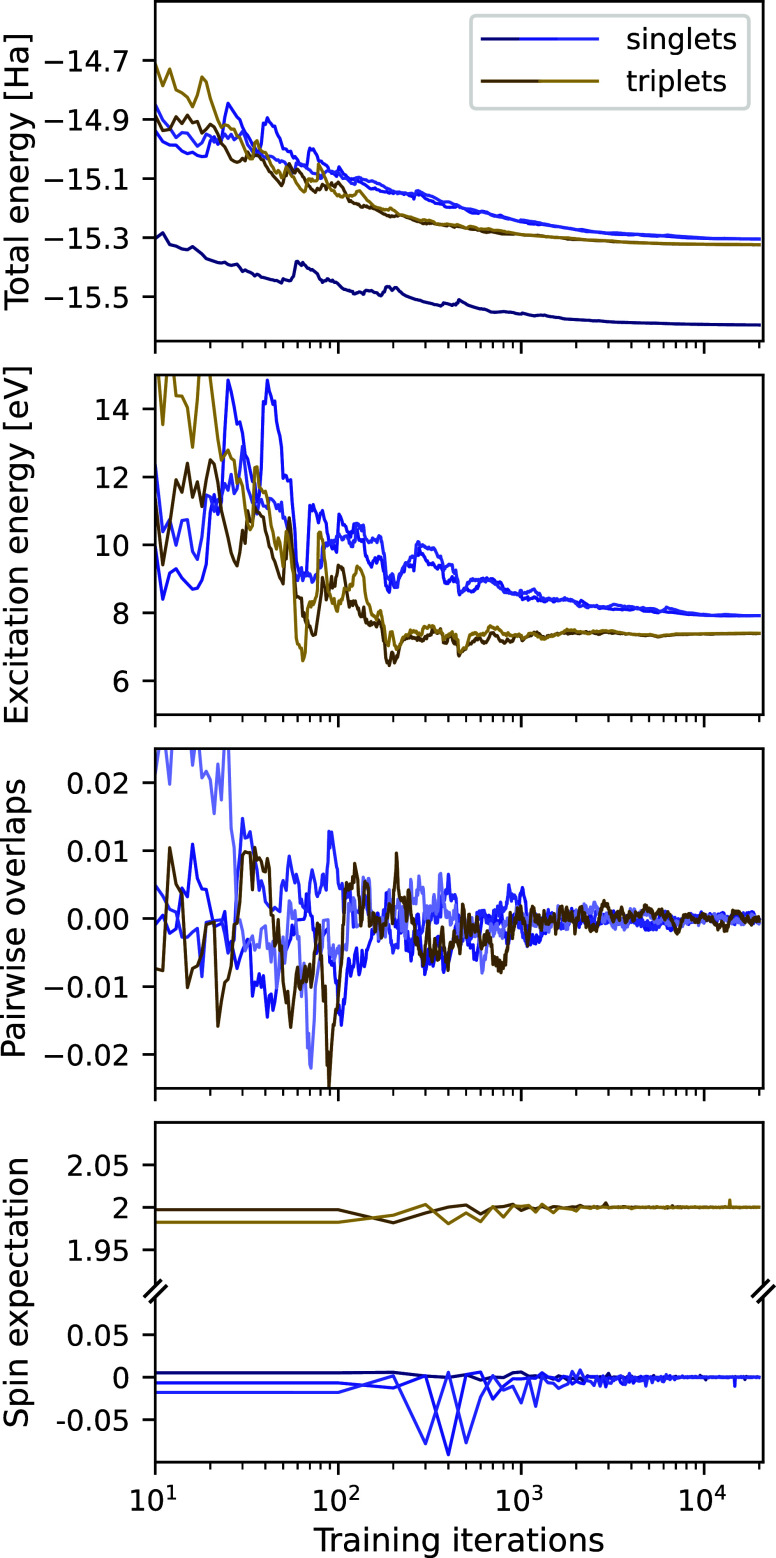
3.1. Convergence of the Penalty-Based Optimization
Before turning to the various benchmark test
sets, it is instructive
to consider the convergence of the relevant quantities throughout
the penalty-based excited-state VMC computation, in order to gain
an intuitive understanding of the method. In Figure 2, the evolution of the total energy, the
excitation energy, the pairwise overlaps and the spin expectation
value are depicted throughout a VMC optimization for the lowest five
states of the HCl molecule. The lowest excited states of HCl are 2-fold
degenerate triplet states followed by a set of doubly degenerate singlet
states, leading to several interesting characteristics of the molecular
spectrum. The spin penalty term is utilized, and two separate simulations
are performed for the singlet (3 states) and triplet (2 states) spin
sector. The ansatzes for the triplet states are assigned two unpaired
spin-up electrons, ensuring that these wave functions will have 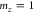 . As usual, the variational
optimization
is preceded by a short supervised pretraining. It can be seen that
all three terms entering the loss function converge smoothly to their
optimal values. Due to the pretraining, the states start off approximately
orthogonal and within the correct spin sector, which is maintained
throughout the optimization. The excitation energies converge rapidly
and stabilize after approximately ten thousand training iterations.
Similar training trajectories are obtained for the other experiments
throughout this paper. For a comprehensive evaluation of the optimized
wave function properties, the training is followed by an evaluation
stage, during which the observables of interest are sampled extensively
with fixed wave function parameters. Postprocessing of the wave function,
such as the diagonalization step in the NES-VMC and AW methods, is
not required.
. As usual, the variational
optimization
is preceded by a short supervised pretraining. It can be seen that
all three terms entering the loss function converge smoothly to their
optimal values. Due to the pretraining, the states start off approximately
orthogonal and within the correct spin sector, which is maintained
throughout the optimization. The excitation energies converge rapidly
and stabilize after approximately ten thousand training iterations.
Similar training trajectories are obtained for the other experiments
throughout this paper. For a comprehensive evaluation of the optimized
wave function properties, the training is followed by an evaluation
stage, during which the observables of interest are sampled extensively
with fixed wave function parameters. Postprocessing of the wave function,
such as the diagonalization step in the NES-VMC and AW methods, is
not required.
Figure 2.
Convergence of relevant quantities throughout the optimization. Two penalty-based excited-state VMC computations are carried out to characterize the lowest three singlet and two triplet electronic states of the HCl molecule. The plotted quantities from top to bottom: total energies, energies of the excitations from the ground state, pairwise overlaps, and the expectation values of the spin magnitude operator.
3.2. Single Point Calculations
3.2.1. Atoms
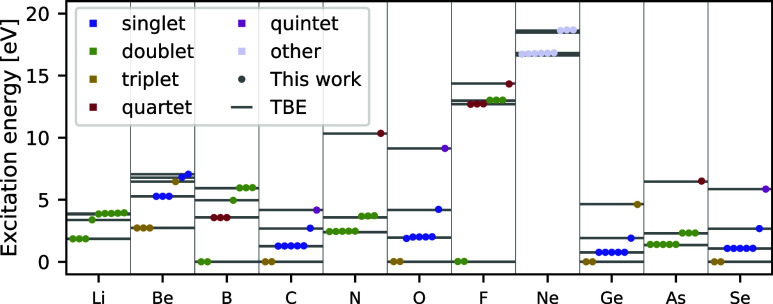
In this section, we demonstrate the capability of the penalty-based excited-state method to model an extended number of excited states simultaneously by computing the lowest nine excitation energies of a range of first- and third-row atoms (lithium to neon and germanium to selenium). We employ highly accurate, experimentally determined atomic spectral lines as reference, after removing the effect of spin–orbit coupling by weighted averaging of the finely split levels. For the first-row atoms, all electrons are included in the computations, while for the third-row atoms, the electrons occupying the three lowest shells are replaced with the ccECP pseuodopotential.47
The computed excitation energies are plotted in Figure 3, alongside the reference experimental data. It is clear that these excitation energies provide a quantitatively correct description of all states in question. To further asses the accuracy of our method we examine the mean absolute errors (MAEs) of the excitation energies for the atoms obtained with different methods in Table 1. We find that on the subset of first row atoms NES-VMC exhibits an advantage with 17 meV (0.39 kcal/mol), compared to the 37 meV (0.86 kcal/mol) of penalty-based VMC. The impressive accuracy of NES-VMC was achieved24 by performing twice as many training iterations as is done in the present work. It is plausible that the accuracy of the penalty-based method would continue to improve similarly with additional training steps. Considering the distribution of errors across the different excitation energies, it becomes apparent that the NES-VMC method tends to accumulate most of its error in the highest computed excited state. In contrast, the penalty-based method offers an advantageous, relatively uniform description of all states. With a maximum error of 166 meV (3.8 kcal/mol), the penalty-based method appears to suffer less from the occasional outliers present in the NES-VMC results, which exhibit a maximum error of 263 meV (6.1 kcal/mol). Inspecting the individual states more closely, the errors of the sharpest outliers in the NES-VMC results (the highest computed states of boron and fluor) are improved by more than a factor of 2 and six, respectively, in the present work. On the contrary, compared to NES-VMC, the penalty-based method appears to encounter slightly more difficulty with highly degenerate states, such as the first quintuple degenerate excited state of nitrogen. This is presumably due to the accumulating noise from the numerous terms in the loss function, derived from the overlaps between states that are very close in energy. Consequently, this noise in the gradients of the loss hinders the convergence of the degenerate states, leading to overestimated excitation energies. This issue is somewhat mitigated by scaling the weight of these loss terms by the energy difference between the given states, as described in Section 2.1.2, to achieve a MAE of 72 meV (1.7 kcal/mol) for these five excitation energies. While we generally found the variance matching scheme introduced alongside the first version of penalty-based VMC for excited-states22 to not be necessary, it can help improving the accuracy for highly degenerate states. If one were to apply this variance matching, the MAE for the five degenerate excitation energies of nitrogen would be reduced to just 14 meV (0.34 kcal/mol). Fortunately, electronic states with this level of degeneracy are exceedingly rare in molecular systems outside of single atoms, therefore we do not expect this to pose a serious limitation to the method in practice. Lastly, we note that as opposed to the first published version of penalty-based excited-state VMC with neural-network ansatzes,22 here all states of the lithium atom are found correctly.
Figure 3.
Excitation energies of first- and third-row atoms. The lowest nine electronic excitation energies are computed for all first-row, and a range of third-row (Ge–Se) atoms. Experimental reference values from the NIST Atomic Spectra Database are depicted with gray horizontal lines,46 while dots display the results of the present work, with colors denoting the spin of the given excited state.
Table 1. Accuracy Comparison Between Various Excited-State VMC Methods on Vertical Excitation Energies of the Systems in the Present Studya.
| MAE | MAX | STD | |||
|---|---|---|---|---|---|
| test set | subset | method | [meV] | [meV] | [meV] |
| Atoms | First row atoms | NES-VMC | 17 | 263 | 37 |
| This work | 37 | 166 | 43 | ||
| Li–O, 10 states | Sequential PB | 39 | 107 | 39 | |
| This work | 31 | 140 | 37 | ||
| Li–O, 5 states | PauliNet | 85 | 518 | 120 | |
| This work | 21 | 85 | 32 | ||
| Ge–Se | Sequential PB | 28 | 50 | 25 | |
| This work | 21 | 64 | 25 | ||
| All atoms | This work | 33 | 166 | 40 | |
| Molecules | without BeH | NES-VMC | 34 | 284 | 67 |
| This work | 45 | 176 | 60 | ||
| without BeH, C6H6 | NES-VMC | 33 | 284 | 69 | |
| This work | 32 | 90 | 37 | ||
| BH, H2O, CO | PauliNet | 134 | 258 | 103 | |
| This work | 27 | 58 | 26 | ||
| BeH, CO, H2O, H2S, H2CSi | Sequential PB | 73 | 153 | 86 | |
| This work | 24 | 58 | 23 | ||
| All molecules | This work | 45 | 176 | 60 |
The last three columns contain the mean absolute errors, maximum errors, and standard deviation of errors in the excitation energies, respectively, for the given method in units of meV. Results of the sequential variant of the penalty-based method are taken from Liu et al.,23 penalty-based numbers with the PauliNet ansatz are reproduced from Entwistle et al.,22 while NES-VMC results are taken from Pfau et al.24 Partitioning of the systems into subsets is necessary as the various works considered slightly different sets of atoms and molecules.
Comparing now with the sequential variant of the penalty-based method for excited states23 on the first row atoms from lithium up to oxygen, the present work achieves a favorable MAE of 31 meV (0.72 kcal/mol) compared to 39 meV (0.90 kcal/mol). The additional error likely arises from the use of pseudopotentials, particularly in combination with the lightest atoms, where the energies of the two core electrons are not sufficiently separated from the valence energies for the pseudopotential approximation to be fully valid. Turning to the third-row atoms, where both works employ pseudopotentials, one finds slightly lower MAEs of 21 meV (0.48 kcal/mol) and 28 meV (0.64 kcal/mol) for the present and the sequential penalty-based results, respectively. Considering the results on the atomic systems overall, the updated penalty-based VMC method appears capable of describing as many as ten, often highly degenerate electronic states simultaneously, at a high level of accuracy.
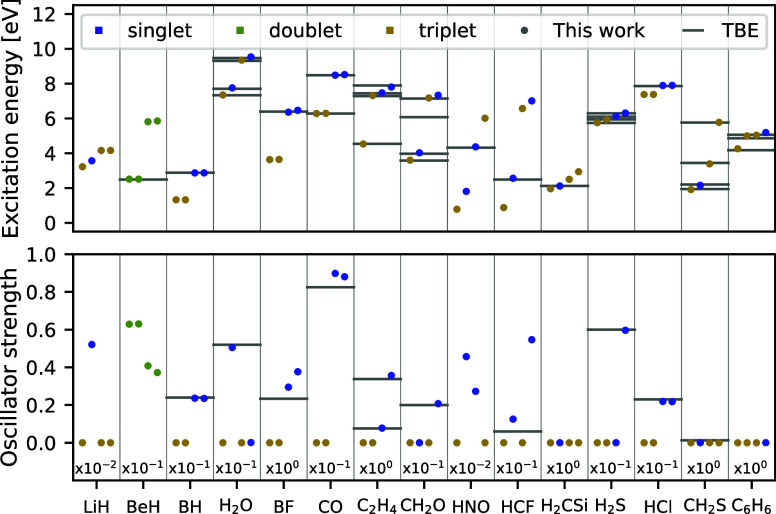
3.2.2. Molecules
Next, the five lowest-lying excited states of 15 molecules are considered, with system sizes ranging from 4 to 42 electrons. The geometries of LiH and BeH are taken from Entwistle et al.,22 benzene is taken from the work of Loos49 et al., while the remaining 12 geometries are taken from Chrayteh et al.50 The latter two publications also provide a number of accurate excitation energies in the complete basis set limit, and oscillator strengths in a triple-zeta quality basis, both obtained with high-order coupled cluster methods, which serve as references here. The statistical measures of accuracy for molecules displayed in Table 1 are computed only for the states where reference data is available (see the horizontal lines of Figure 4). Electrons from the first two shells of second-row atoms are replaced with the ccECP potential.29 It should be noted that, especially in the case of oscillator strengths, reference values obtained with different basis sets or at different orders of the coupled cluster expansion may exhibit wider disparities than the differences between the investigated QMC methods, highlighting the difficulty of reliably estimating these quantities.
Figure 4.
Excitation energies and oscillator strengths of main-group molecules. Electronic excitation energies and oscillator strengths are computed for the lowest four transitions in a set of 15 molecules. Theoretical best estimates are depicted with gray horizontal lines where available,48 while the predictions of penalty-based VMC are displayed with dots, with colors denoting the spin of the corresponding excited state. Excitation energies are plotted on the top pane, while oscillator strengths are shown on the bottom pane.
On the top pane of Figure 4, the first four vertical excitation energies of the 15 molecules in question are plotted. Similar to the findings for atoms, we observe that both the NES and penalty-based methods yield excitation energies in very good agreement with the theoretical best estimates. As demonstrated in Table 1, when compared to the atomic test set, the MAEs of the two methods are somewhat closer for the molecules, measuring at 34 meV (0.78 kcal/mol) for NES-VMC and 45 meV (1.0 kcal/mol) for penalty-based VMC. This closing of the accuracy gap can largely be attributed to the absence of highly degenerate states in molecules, which were the primary cause of noisy and outlier states in the atomic systems. In terms of errors made on individual molecules and states, the penalty-based excited-state method shows improvement over the potentially misconverged highest tioformaldehyde state of NES-VMC. Additionally, it performs slightly better on the third excitation energy of nitroxyl. However, it does make larger errors on benzene, as well as on the highest states of formaldehyde and ethylene. It is worth noting that despite the two methods exhibiting very similar MAEs, their error distributions are quite different. The predictions of the NES-VMC method exhibit slightly lower errors than those of the penalty-based method for the majority of systems, but at the same time contain more severe outliers for a handful of states. In contrast, the penalty-based approach tends to produce relatively uniform errors, which could conceivably be further reduced by conducting more training iterations. This trend is also evident in the slightly larger standard deviation of errors for NES-VMC. Interestingly, both VMC-based methods fail to capture the 3A1 state of formaldehyde (both with FermiNet and Psiformer), potentially indicating a more fundamental issue with the description of this state, which warrants further research. The fact that the failure to describe this state is reproducible across different ansatz architectures, loss functions, and pretraining schemes points to a more general optimization problem associated with this electronic state. It is conceivable that the minimum of the loss function corresponding to this state is especially narrow or shallow, making it difficult to locate with stochastic gradient based optimization methods. For convergence curves, reference and baseline CASSCF excitation energies obtained for this state see the Supporting Information.
Turning now to the oscillator strengths plotted on the bottom pane of Figure 4, one finds a generally good agreement between the penalty-based excited-state VMC method and the reference results, with a few notable exceptions. Specifically, the intensity of the highest two transitions of carbon monoxide and boron monofluoride are overestimated by penalty-based VMC compared to coupled cluster. For certain excitations of the LiH, BeH, HNO, and HCF molecules, the lack of accurate reference data makes it difficult to ascertain the performance of the penalty-based excited-state VMC method. Nonetheless, the generally accurate oscillator strength estimates obtained from the penalty-based method serve as compelling evidence that it not only delivers accurate energies but also well-converged wave functions, which can be of great use in computing a wide range of observable quantities of excited states. Furthermore, it is clear that contrary to previous hypothesis,24 the penalty-based method is competitive with the NES-VMC approach when employing the same, sufficiently expressive ansatz in both cases.
3.3. Excited-State Potential Energy Surfaces
While performing single-point computations targeting the excited states of molecules is a valuable endeavor in its own right, characterizing portions of molecular excited-state PESs holds even greater significance. Access to these PESs can enable simulations of the evolution of molecular systems in their excited states,52 paving the way for describing crucial photochemical processes such as the light-harvesting step in photovoltaic devices53,54 or the photoisomerization of the retinal chromophore that initiates vision.55 Furthermore, information about the PES is often essential for bridging theoretical results with experimental estimates, in tasks such as determining adiabatic excitation energies or the zero-point vibrational energy correction. Unfortunately, the theoretical characterization of excited-state PESs often presents even greater challenges than a single-point calculation, such as the problem of consistently defining the active space in active-space-based methods, or the treatment of strong correlation near conical intersections in approximate time-dependent density functional theories.22,56 In this section, we will demonstrate how the penalty-based method can be easily applied to compute excited-state molecular PESs for systems with challenging electronic structures.
3.3.1. Excited States of the Carbon Dimer
Despite its small size, the electronic structure of the carbon dimer remains the subject of intensive interest in both experimental58 and theoretical studies.51,59 It exhibits strong multireference character and numerous nearly degenerate low-lying excited states with singlet, triplet and quintet spins, some of which can be characterized as double excitations. Accurately and consistently describing its numerous electronic states across a range of bond lengths presents a challenge tackled only by the most sophisticated electronic structure methods.
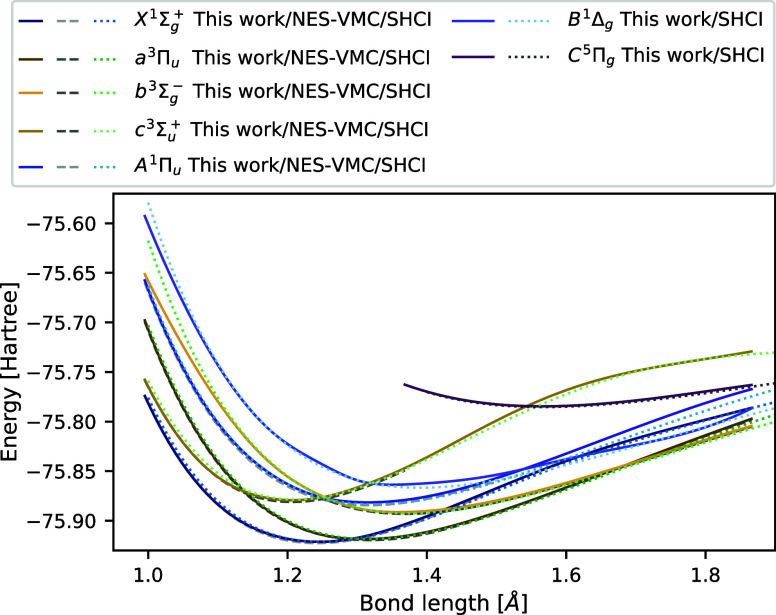
The excited-state
PESs of the carbon dimer, computed using the penalty-based excited-state
method, are shown in Figure 5 with solid lines. The capability of penalty-based VMC to
perform separate computations for states with different spins has
been leveraged to efficiently characterize the lowest four singlet,
four triplet and one quintet states. It is important to note that
two of the singlet and two of the triplet states are degenerate across
the entire range of bond lengths, resulting in only three–three
lines being plotted for these spin sectors. The results reported with
NES-VMC24 are shown in Figure 5 with dashed lines. In regions
where NES-VMC results are available, they are in excellent agreement
with the curves obtained from penalty-based excited-state VMC. Note
that the penalty-based method converges in multiple regions where
its counterpart cannot provide a sufficiently accurate description,
such as the compressed geometries of the 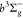 state, the stretched
geometries of the
state, the stretched
geometries of the 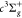 and all singlet states, as well as the
entire
and all singlet states, as well as the
entire 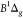 curve. Additionally,
due to the computational
efficiency afforded by the use of the spin penalty, one is able to
describe a section of the lowest-lying quintet
curve. Additionally,
due to the computational
efficiency afforded by the use of the spin penalty, one is able to
describe a section of the lowest-lying quintet 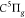 state, including its minimum, by performing
a single-state penalty-based calculation. Considering that both the
state, including its minimum, by performing
a single-state penalty-based calculation. Considering that both the 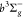 and
and 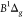 states are characterized
as double excitations,24 a class of excited
states that many other methods
struggle with, the ability of penalty-based VMC to accurately describe
large sections of these PESs is particularly noteworthy.
states are characterized
as double excitations,24 a class of excited
states that many other methods
struggle with, the ability of penalty-based VMC to accurately describe
large sections of these PESs is particularly noteworthy.
Figure 5.
Excited potential energy surfaces of the carbon dimer. Potential energy surfaces for nine of the low-lying excited states of the carbon dimer are calculated. Solid lines represent penalty-based excited-state VMC results, dashed curves were obtained using NES-VMC,20 and dotted lines depict semistochastic heat-bath configuration interaction results in the cc-pV5Z basis.51
Comparing the predictions
of the penalty-based excited-state method
with results obtained using the highly accurate stochastic heat-bath
configuration interaction (SHCI) approach51 shown with dotted lines in Figure 5, one finds excellent agreement for most geometries
of all states. Notable exceptions are the high-lying compressed regions
of the 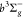 state, and the stretched regions of the
state, and the stretched regions of the 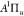 and
and 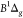 curves. For
the compressed geometries,
the VMC-based method underestimates the excitation energies, while
for the stretched geometries, it delivers slightly higher estimates.
In the stretched geometries of the singlet states, we observe higher-than-usual
variance in the expectation of the energy during training, indicating
potential problems with the fitting of these states, whereas we identified
no such signals for the compressed triplet states. Overall, the accuracy
of the penalty-based method appears to be on par with that of NES-VMC
and comparable with the SHCI reference. Additionally, its consistency
and ability to target specific spin states enable it to deliver results
on larger section of the carbon dimer PESs than its VMC-based counterpart.
curves. For
the compressed geometries,
the VMC-based method underestimates the excitation energies, while
for the stretched geometries, it delivers slightly higher estimates.
In the stretched geometries of the singlet states, we observe higher-than-usual
variance in the expectation of the energy during training, indicating
potential problems with the fitting of these states, whereas we identified
no such signals for the compressed triplet states. Overall, the accuracy
of the penalty-based method appears to be on par with that of NES-VMC
and comparable with the SHCI reference. Additionally, its consistency
and ability to target specific spin states enable it to deliver results
on larger section of the carbon dimer PESs than its VMC-based counterpart.
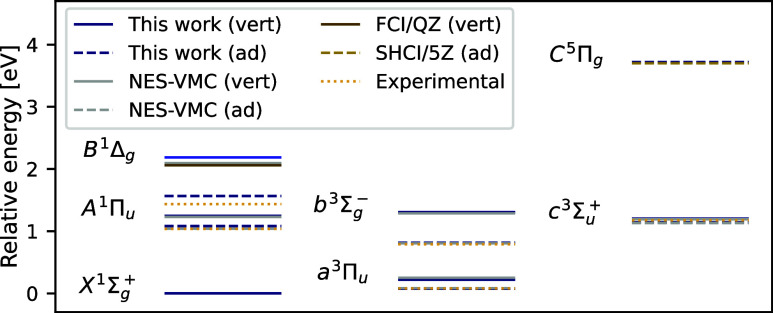
The vertical and adiabatic excitation energies from the ground
state to the considered excited states of the carbon dimer are plotted
in Figure 6. The relative
energies obtained from penalty-based VMC are in good agreement with
both NES-VMC and, where applicable, reference experimental,57 full configuration interaction,49 and SHCI results.51 The discrepancies
between the penalty-based method and the appropriate references are
well below 43 meV (1.0 kcal/mol) for all states except for 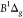 , where both
the vertical and adiabatic
excitation energies are overestimated by penalty-based VMC by about
100 meV (2.3 kcal/mol).
, where both
the vertical and adiabatic
excitation energies are overestimated by penalty-based VMC by about
100 meV (2.3 kcal/mol).
Figure 6.
Vertical and adiabatic excitation energies of the carbon dimer. Vertical (vert) excitation energies are plotted with solid, adiabatic (ad) ones with dashed, and experimental ones with dotted lines. The zero-point vibrational energy was not considered during the computation of the adiabatic excitation energies. The penalty-based VMC predictions are compared with results obtained from NES-VMC,24 full-configuration interaction using the cc-pVQZ basis,49 semistochastic heat-bath configuration interaction with the cc-pV5Z basis,51 and experiments.57
3.3.2. Conical Intersection in Ethylene
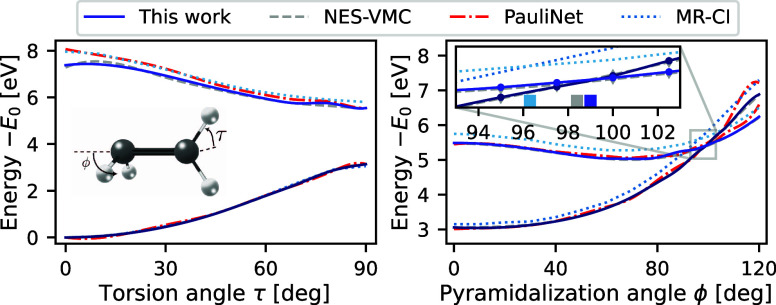
Conical intersections play an important role in the study of excited-state dynamics associated with processes such as photoisomerization and photodissociation, providing a pathway for nonradiative relaxation from electronic photoexcitations. From a computational perspective, conical intersections pose a significant challenge, as the multireference character of the electronic states increases when the potential energy surfaces converge. However, to achieve a good description of the dynamics, an accurate and well-balanced model of the excited-state potential energy surface is crucial. Here we study the conical intersection of ethylene, which serves as a small-scale model system for photoswitches. Upon photoexcitation to the lowest singlet excited state, ethylene undergoes torsion (angle τ) along the C–C bond, followed by pyramidalization (angle ϕ) of one of the CH2 groups, as depicted in the inset of Figure 7. This leads to a conical intersection, where a radiationless transition to the ground-state potential energy surface occurs.60 The process involves intricate changes in the electronic structure that pose well-known problems for single-reference methods such as TDDFT.61 While our focus lies on the study of the singlet states, the simulations are further complicated by the presence of multiple lower-lying triplet states.
Figure 7.
Conical intersection of ethylene. The energies of the lowest two singlet states of ethylene are plotted as a function of the torsion and pyramidalization angles, relative to the energy of the ground state at the equilibrium geometry. Results obtained with the updated penalty-based method are plotted alongside those of the original version with the PauliNet ansatz,22 NES-VMC,24 and multireference configuration interaction with single and double excitations.60 The inset plot on the right pane shows the region around the conical intersection, with the vertical lines marking the approximate location of the conical intersection.
To address this, we employ the
spin penalty method to restrict
our calculations to the singlet sector, ensuring that no more than
one excited state need to be computed at any point along the trajectory.
The results are compared with accurate multireference configuration
interaction (MR-CI) calculations60 and
previous studies with neural-network VMC.22,24Figure 7 shows the
energies of the ground state and the first excited state relative
to the ground-state energy at the equilibrium geometry. Our results
are in excellent agreement with the NES-VMC method, representing a
significant improvement over previous calculations using penalty-based
VMC.22 The avoided crossing at 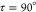 is well
reproduced, and the excitation
energy of 2.41 eV is within 0.01 eV of the NES-VMC result. Furthermore,
we estimate the location of the conical intersection to be between
97.5◦ and 100◦ (
is well
reproduced, and the excitation
energy of 2.41 eV is within 0.01 eV of the NES-VMC result. Furthermore,
we estimate the location of the conical intersection to be between
97.5◦ and 100◦ (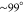 ), bringing it closer
to the MR-CI reference
(
), bringing it closer
to the MR-CI reference
(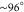 ) and being in good agreement
with the NES-VMC
result(
) and being in good agreement
with the NES-VMC
result(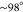 ). We note that while
the study of ethylene
with NES-VMC required simulations for three excited states across
the PES and a special treatment of the equilibrium geometry, we do
not need to compute additional states and run all single-point calculations
along the trajectory with the same parameters. The good agreement
with NES-VMC and qualitative reproduction of the MR-CI results indicate
that the penalty-based method is capable of accurately modeling the
complicated electronic structure of the ethylene isomerization process.
). We note that while
the study of ethylene
with NES-VMC required simulations for three excited states across
the PES and a special treatment of the equilibrium geometry, we do
not need to compute additional states and run all single-point calculations
along the trajectory with the same parameters. The good agreement
with NES-VMC and qualitative reproduction of the MR-CI results indicate
that the penalty-based method is capable of accurately modeling the
complicated electronic structure of the ethylene isomerization process.
4. Discussion
An updated version of the deep-learning penalty-based excited-state VMC method is presented and applied to compute a wide range of atomic and molecular excited states, demonstrating its enhanced accuracy and attractive computational properties. The improvements include the use of a new state-of-the-art attention-based neural network ansatz, systematic tuning of the optimizer hyperparameters, and an updated overlap penalty term that guarantees the global minimum of the loss function yields the exact solution of the electronic structure problem. The method’s dependence on the choice of free parameters is greatly reduced by a formulation that automatically adapts these parameters to the physical system under consideration. Lastly, a new penalty term is introduced which, in combination with a spin-assigned ansatz, enables the targeting of specific spin states, significantly improving the computational efficiency in many applications.
The computational aspects of the penalty-based method are examined in relation to other prevalent VMC-based algorithms for computing molecular excited states. Compared to NES-VMC, penalty-based methods exhibit favorable scaling with the number of computed electronic states, due to the former approach’s need to model and sample an extended system of Fermions. On the other hand, a remaining weak dependence on the choice of scaling parameters and accumulating noise from the penalty terms in rare, highly degenerate systems can cause comparatively worse numerical issues for the penalty-based method in a limited number of cases. In contrast to variance minimization approaches, penalty-based methods do not require additional approximations to obtain stable gradients. The approach presented here is more practical than both the NES-VMC algorithm, as it requires no additional diagonalization to recover the individual states, and the sequential variant of the penalty-based method, as it replaces a set of sequential calculations with a single parallel one, granting access to all electronic states at every stage of the computation.
The accuracy of results obtained with the penalty-based method is compared to both accurate reference values and numbers obtained with other deep-learning VMC-based approaches. On a set of first- and third-row atoms, where practically exact experimental references are available, penalty-based excited-state VMC recovers the lowest nine excitation energies with a mean absolute error of less than 1 kcal/mol. Its accuracy is on par with its sequential variant, and is comparable to that of the NES-VMC method, even though fewer training iterations are carried out here. For 15 small to medium molecules, deviations from theoretical reference energies remain well under control, while the reliably accurate oscillator strengths indicate consistently high wave function quality across a wide range of systems. Considering excited-state potential energy surfaces, the efficiency and black-box nature of the penalty-based method in tackling this traditionally challenging class of problems become evident. Large sections of nine carbon dimer potential energy surfaces with singlet, triplet, and quintet spins between bond lengths of 1.0 and 1.9 Å are accurately recovered. The derived vertical and adiabatic excitation energies are in good agreement with both experimental and theoretical reference values. Turning to the ethylene potential energy surfaces, the updated penalty-based method significantly improves on results obtained with earlier versions and predicts the position of the conical intersection in good agreement with MR-CI and NES-VMC. The description of both the carbon dimer and ethylene potential energy surfaces is made significantly more efficient by the use of the spin penalty term, roughly halving the number of states needed to be considered simultaneously in any single computation.
Overall, the computational advantages and accurate predictions of deep-learning penalty-based VMC place it among the most promising methods for computing electronic excited states with VMC. Notably, it delivers similar accuracy to the NES-VMC method when the same neural-network ansatzes are used in both algorithms, while offering several practical advantages. Given the recent surge in interest in deep-learning excited-state VMC for molecular electronic structure, the penalty-based approach is poised to become a prominent method for describing the most challenging excited states of small to medium molecules.
Acknowledgments
We thank Alice Cuzzocrea and Paolo Erdman for helpful discussions. Funding is gratefully acknowledged from Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – The Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689) projects (AA1-6, AA2-8) and Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) project NO825/3-2. The authors gratefully acknowledge the computing time granted by the Resource Allocation Board and provided on the supercomputer Lise at NHR@ZIB as part of the NHR infrastructure. The calculations for this research were conducted with computing resources under the project bec00266.
Data Availability Statement
The computer code for the calculations of this study will be made publicly available in the DeepQMC repository38 upon publication of the manuscript.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.4c00678.
The obtained total energies for all reported calculations, convergence curves for the simulated states of the formaldehyde molecule, a summary of the training hyperparameters used throughout this work, as well as a brief discussion on the use of spin assigned wave functions in quantum Monte Carlo (PDF)
Author Contributions
# P.B.S. and Z.S. equal contribution.
The authors declare no competing financial interest.
Supplementary Material
References
- Matsika S.; Krylov A. I. Introduction: Theoretical Modeling of Excited State Processes. Chem. Rev. 2018, 118, 6925–6926. 10.1021/acs.chemrev.8b00436. [DOI] [PubMed] [Google Scholar]
- Lu P.; Ahn D.; Yunis R.; Delafresnaye L.; Corrigan N.; Boyer C.; Barner-Kowollik C.; Page Z. A. Wavelength-Selective Light-Matter Interactions in Polymer Science. Matter 2021, 4, 2172–2229. 10.1016/j.matt.2021.03.021. [DOI] [Google Scholar]
- Kancherla R.; Muralirajan K.; Sagadevan A.; Rueping M. Visible Light-Induced Excited-State Transition-Metal Catalysis. Trends Chem. 2019, 1, 510–523. 10.1016/j.trechm.2019.03.012. [DOI] [Google Scholar]
- Stirbet A.; Lazár D.; Guo Y.; Govindjee G. Photosynthesis: Basics, History and Modelling. Ann. Bot. 2020, 126, 511–537. 10.1093/aob/mcz171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capel-Sanchez M.; Blanco-Brieva G.; Campos-Martin J. M.; Fierro J. L. G. The Usefulness of Time-Dependent Density Functional Theory to Describe the Electronic Spectra of Ti-Containing Catalysts. Angew. Chem., Int. Ed. 2003, 42, 5851–5854. 10.1002/anie.200351452. [DOI] [PubMed] [Google Scholar]
- Schoenlein R. W.; Peteanu L. A.; Mathies R. A.; Shank C. V. The First Step in Vision: Femtosecond Isomerization of Rhodopsin. Science 1991, 254, 412–415. 10.1126/science.1925597. [DOI] [PubMed] [Google Scholar]
- Vasil’ev S.; Orth P.; Zouni A.; Owens T. G.; Bruce D. Excited-State Dynamics in Photosystem II: Insights from the x-Ray Crystal Structure. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 8602–8607. 10.1073/pnas.141239598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curutchet C.; Mennucci B. Quantum Chemical Studies of Light Harvesting. Chem. Rev. 2017, 117, 294–343. 10.1021/acs.chemrev.5b00700. [DOI] [PubMed] [Google Scholar]
- Kundu S.; Patra A. Nanoscale Strategies for Light Harvesting. Chem. Rev. 2017, 117, 712–757. 10.1021/acs.chemrev.6b00036. [DOI] [PubMed] [Google Scholar]
- Fomina N.; Sankaranarayanan J.; Almutairi A. Photochemical Mechanisms of Light-Triggered Release from Nanocarriers. Adv. Drug Delivery Rev. 2012, 64, 1005–1020. 10.1016/j.addr.2012.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogomolny E.; Mordechai S.; Zwielly A.; Huleihel M. Early Detection of Premalignant Changes in Cell Cultures Using Light-Induced Fluorescence Spectroscopy. Eur. Biophys. J. 2009, 38, 971–980. 10.1007/s00249-009-0488-z. [DOI] [PubMed] [Google Scholar]
- Mai S.; González L. Molecular Photochemistry: Recent Developments in Theory. Angew. Chem., Int. Ed. 2020, 59, 16832–16846. 10.1002/anie.201916381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González L.; Escudero D.; Serrano-Andrés L. Progress and Challenges in the Calculation of Electronic Excited States. ChemPhyschem 2012, 13, 28–51. 10.1002/cphc.201100200. [DOI] [PubMed] [Google Scholar]
- Lischka H.; Nachtigallová D.; Aquino A. J. A.; Szalay P. G.; Plasser F.; Machado F. B. C.; Barbatti M. Multireference Approaches for Excited States of Molecules. Chem. Rev. 2018, 118, 7293–7361. 10.1021/acs.chemrev.8b00244. [DOI] [PubMed] [Google Scholar]
- Ullrich C. A.Time-Dependent Density-Functional Theory: concepts and Applications; OUP Oxford, 2011. [Google Scholar]
- Liang J.; Feng X.; Hait D.; Head-Gordon M. Revisiting the Performance of Time-Dependent Density Functional Theory for Electronic Excitations: Assessment of 43 Popular and Recently Developed Functionals from Rungs One to Four. J. Chem. Theory Comput. 2022, 18, 3460–3473. 10.1021/acs.jctc.2c00160. [DOI] [PubMed] [Google Scholar]
- Laurent A. D.; Jacquemin D. TD-DFT Benchmarks: A Review. Int. J. Quantum Chem. 2013, 113, 2019–2039. 10.1002/qua.24438. [DOI] [Google Scholar]
- Keller S.; Boguslawski K.; Janowski T.; Reiher M.; Pulay P. Selection of Active Spaces for Multiconfigurational Wavefunctions. J. Chem. Phys. 2015, 142, 244104. 10.1063/1.4922352. [DOI] [PubMed] [Google Scholar]
- Hermann J.; Schätzle Z.; Noé F. Deep-Neural-Network Solution of the Electronic Schrödinger Equation. Nat. Chem. 2020, 12, 891–897. 10.1038/s41557-020-0544-y. [DOI] [PubMed] [Google Scholar]
- Pfau D.; Spencer J. S.; Matthews A. G. D. G.; Foulkes W. M. C. Ab Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks. Phys. Rev. Res. 2020, 2, 033429. 10.1103/PhysRevResearch.2.033429. [DOI] [Google Scholar]
- Hermann J.; Spencer J.; Choo K.; Mezzacapo A.; Foulkes W. M. C.; Pfau D.; Carleo G.; Noé F. Ab Initio Quantum Chemistry with Neural-Network Wavefunctions. Nat. Rev. Chem. 2023, 7, 692–709. 10.1038/s41570-023-00516-8. [DOI] [PubMed] [Google Scholar]
- Entwistle M. T.; Schätzle Z.; Erdman P. A.; Hermann J.; Noé F. Electronic Excited States in Deep Variational Monte Carlo. Nat. Commun. 2023, 14, 274. 10.1038/s41467-022-35534-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J.; Qin C.; He X.; Jiang G. Calculate Electronic Excited States Using Neural Networks with Effective Core Potential. arXiv 2023, 10.48550/arXiv.2312.15216. [DOI] [Google Scholar]
- Pfau D.; Axelrod S.; Sutterud H.; von Glehn I.; Spencer J. S. Natural Quantum Monte Carlo Computation of Excited States. arXiv 2024, 10.48550/arXiv.2308.16848. [DOI] [PubMed] [Google Scholar]
- Wheeler W. A.; Kleiner K. G.; Wagner L. K. Ensemble Variational Monte Carlo for Optimization of Correlated Excited State Wave Functions. Electron. Struct. 2024, 6, 025001. 10.1088/2516-1075/ad38f8. [DOI] [Google Scholar]
- Lu Z.; Fu W. Penalty and Auxiliary Wave Function Methods for Electronic Excitation in Neural Network Variational Monte Carlo. arXiv 2023, 10.48550/arXiv.2311.17595. [DOI] [Google Scholar]
- von Glehn I.; Spencer J. S.; Pfau D.. A Self-Attention Ansatz for Ab-initio Quantum Chemistry. arXiv, 2022. 10.48550/arXiv.2211.13672. [DOI] [Google Scholar]
- Martens J.; Grosse R.. Optimizing Neural Networks with Kronecker-factored Approximate Curvature. Proceedings Of The 32nd International Conference On Machine Learning, PMLR, 20152408–2417.. [Google Scholar]
- Annaberdiyev A.; Wang G.; Melton C. A.; Bennett M. C.; Shulenburger L.; Mitas L. A New Generation of Effective Core Potentials from Correlated Calculations: 3d Transition Metal Series. J. Chem. Phys. 2018, 149, 134108. 10.1063/1.5040472. [DOI] [PubMed] [Google Scholar]
- Wang G.; Annaberdiyev A.; Melton C. A.; Bennett M. C.; Shulenburger L.; Mitas L. A New Generation of Effective Core Potentials from Correlated Calculations: 4s and 4p Main Group Elements and First Row Additions. J. Chem. Phys. 2019, 151, 144110. 10.1063/1.5121006. [DOI] [PubMed] [Google Scholar]
- Schätzle Z.; Szabó P. B.; Mezera M.; Hermann J.; Noé F. DeepQMC: An Open-Source Software Suite for Variational Optimization of Deep-Learning Molecular Wave Functions. J. Chem. Phys. 2023, 159, 094108. 10.1063/5.0157512. [DOI] [PubMed] [Google Scholar]
- Pathak S.; Busemeyer B.; Rodrigues J. N. B.; Wagner L. K. Excited States in Variational Monte Carlo Using a Penalty Method. J. Chem. Phys. 2021, 154, 034101. 10.1063/5.0030949. [DOI] [PubMed] [Google Scholar]
- Choo K.; Carleo G.; Regnault N.; Neupert T. Symmetries and Many-Body Excitations with Neural-Network Quantum States. Phys. Rev. Lett. 2018, 121, 167204. 10.1103/PhysRevLett.121.167204. [DOI] [PubMed] [Google Scholar]
- Umrigar C. J.; Wilson K. G.; Wilkins J. W. Optimized Trial Wave Functions for Quantum Monte Carlo Calculations. Phys. Rev. Lett. 1988, 60, 1719–1722. 10.1103/PhysRevLett.60.1719. [DOI] [PubMed] [Google Scholar]
- Umrigar C. J.; Filippi C. Energy and Variance Optimization of Many-Body Wave Functions. Phys. Rev. Lett. 2005, 94, 150201. 10.1103/PhysRevLett.94.150201. [DOI] [PubMed] [Google Scholar]
- Cuzzocrea A.; Scemama A.; Briels W. J.; Moroni S.; Filippi C. Variational Principles in Quantum Monte Carlo: The Troubled Story of Variance Minimization. J. Chem. Theory Comput. 2020, 16, 4203–4212. 10.1021/acs.jctc.0c00147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser L.; Polosukhin I.. Attention Is All You Need. In Advances in Neural Information Processing Systems 30 (NIPS 2017); NIPS, 2017. [Google Scholar]
- Hermann J.; Szabó P. B.; Schätzle Z.; Mezera M.; Foster A.; Maziarz K.; Sauceda H. E.; Brockschmidt M.. DeepQMC, 2023, https://github.com/deepqmc/deepqmc.
- Dunning T. H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Kendall R. A.; Dunning T. H.; Harrison R. J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. 10.1063/1.462569. [DOI] [Google Scholar]
- Wilson A. K.; Woon D. E.; Peterson K. A.; Dunning T. H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. IX. The Atoms Gallium through Krypton. J. Chem. Phys. 1999, 110, 7667–7676. 10.1063/1.478678. [DOI] [Google Scholar]
- Sun Q.; Zhang X.; Banerjee S.; Bao P.; Barbry M.; Blunt N. S.; Bogdanov N. A.; Booth G. H.; Chen J.; Cui Z.-H.; Eriksen J. J.; Gao Y.; Guo S.; Hermann J.; Hermes M. R.; Koh K.; Koval P.; Lehtola S.; Li Z.; Liu J.; Mardirossian N.; McClain J. D.; Motta M.; Mussard B.; Pham H. Q.; Pulkin A.; Purwanto W.; Robinson P. J.; Ronca E.; Sayfutyarova E. R.; Scheurer M.; Schurkus H. F.; Smith J. E. T.; Sun C.; Sun S.-N.; Upadhyay S.; Wagner L. K.; Wang X.; White A.; Whitfield J. D.; Williamson M. J.; Wouters S.; Yang J.; Yu J. M.; Zhu T.; Berkelbach T. C.; Sharma S.; Sokolov A. Y.; Chan G. K.-L. Recent Developments in the PySCF Program Package. J. Chem. Phys. 2020, 153, 024109. 10.1063/5.0006074. [DOI] [PubMed] [Google Scholar]
- Huang C.-J.; Filippi C.; Umrigar C. J. Spin Contamination in Quantum Monte Carlo Wave Functions. J. Chem. Phys. 1998, 108, 8838–8847. 10.1063/1.476330. [DOI] [Google Scholar]
- Bradbury J.; Frostig R.; Hawkins P.; Johnson M. J.; Leary C.; Maclaurin D.; Necula G.; Paszke A.; VanderPlas J.; Wanderman-Milne S.. JAX: composable Transformations Of Python + NumPy Programs, 2018. http://github.com/google/jax
- Spencer J. S.; Pfau D.. FermiNet Contributors, Google-Deepmind/ferminet, 2020. https://github.com/google-deepmind/ferminet.
- Kramida A.; Ralchenko Y. U.; Reader J., NIST ASD Team, NIST Atomic Spectra Database NIST Atomic Spectra Database (ver. 5.11), [Online]; National Institute of Standards and Technology: Gaithersburg, MD, 2023. https://physics.nist.gov/asd. [Google Scholar]
- Bennett M. C.; Melton C. A.; Annaberdiyev A.; Wang G.; Shulenburger L.; Mitas L. A New Generation of Effective Core Potentials for Correlated Calculations. J. Chem. Phys. 2017, 147, 224106. 10.1063/1.4995643. [DOI] [PubMed] [Google Scholar]
- Véril M.; Scemama A.; Caffarel M.; Lipparini F.; Boggio-Pasqua M.; Jacquemin D.; Loos P.-F. QUESTDB: A Database of Highly-Accurate Excitation Energies for the Electronic Structure Community. WIREs Comput. Mol. Sci. 2021, 11, e1517 10.1002/wcms.1517. [DOI] [Google Scholar]
- Loos P.-F.; Lipparini F.; Boggio-Pasqua M.; Scemama A.; Jacquemin D. A Mountaineering Strategy to Excited States: Highly Accurate Energies and Benchmarks for Medium Sized Molecules. J. Chem. Theory Comput. 2020, 16, 1711–1741. 10.1021/acs.jctc.9b01216. [DOI] [PubMed] [Google Scholar]
- Chrayteh A.; Blondel A.; Loos P.-F.; Jacquemin D. Mountaineering Strategy to Excited States: Highly Accurate Oscillator Strengths and Dipole Moments of Small Molecules. J. Chem. Theory Comput. 2021, 17, 416–438. 10.1021/acs.jctc.0c01111. [DOI] [PubMed] [Google Scholar]
- Holmes A. A.; Umrigar C. J.; Sharma S. Excited States Using Semistochastic Heat-Bath Configuration Interaction. J. Chem. Phys. 2017, 147, 164111. 10.1063/1.4998614. [DOI] [PubMed] [Google Scholar]
- Cuzzocrea A.From Vertical Excitations towards Excited-State Relaxation: A Journey with Quantum Monte Carlo PhD thesis; University of Twente, 2022. [Google Scholar]
- Cerullo G.; Polli D.; Lanzani G.; Silvestri S. D.; Hashimoto H.; Cogdell R. J. Photosynthetic Light Harvesting by Carotenoids: Detection of an Intermediate Excited State. Science 2002, 298, 2395–2398. 10.1126/science.1074685. [DOI] [PubMed] [Google Scholar]
- Dahlberg P. D.; Ting P.-C.; Massey S. C.; Allodi M. A.; Martin E. C.; Hunter C. N.; Engel G. S. Mapping the Ultrafast Flow of Harvested Solar Energy in Living Photosynthetic Cells. Nat. Commun. 2017, 8, 988. 10.1038/s41467-017-01124-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao A. G.; Schapiro I. Photoisomerization of Phytochrome Chromophore Models: An XMS-CASPT2 Study. Phys. Chem. Chem. Phys. 2022, 24, 29393–29405. 10.1039/D2CP04249E. [DOI] [PubMed] [Google Scholar]
- Mališ M.; Luber S. Trajectory Surface Hopping Nonadiabatic Molecular Dynamics with Kohn–Sham ΔSCF for Condensed-Phase Systems. J. Chem. Theory Comput. 2020, 16, 4071–4086. 10.1021/acs.jctc.0c00372. [DOI] [PubMed] [Google Scholar]
- Tanabashi A.; Hirao T.; Amano T.; Bernath P. F. The Swan System of C2 : Global Analysis of Fourier Transform Emission Spectra. Astrophys. J., Suppl. Ser. 2007, 169, 472–484. 10.1086/510742. [DOI] [Google Scholar]
- Martin M. C2 Spectroscopy and Kinetics. J. Photochem. Photobiol., A 1992, 66, 263–289. 10.1016/1010-6030(92)80001-C. [DOI] [Google Scholar]
- Sharma S. A General Non-Abelian Density Matrix Renormalization Group Algorithm with Application to the C2 Dimer. J. Chem. Phys. 2015, 142, 024107. 10.1063/1.4905237. [DOI] [PubMed] [Google Scholar]
- Barbatti M.; Paier J.; Lischka H. Photochemistry of Ethylene: A Multireference Configuration Interaction Investigation of the Excited-State Energy Surfaces. J. Chem. Phys. 2004, 121, 11614–11624. 10.1063/1.1807378. [DOI] [PubMed] [Google Scholar]
- Schmerwitz Y. L. A.; Ivanov A. V.; Jónsson E. O.; Jónsson H.; Levi G. Variational Density Functional Calculations of Excited States: Conical Intersection and Avoided Crossing in Ethylene Bond Twisting. J. Phys. Chem. Lett. 2022, 13, 3990–3999. 10.1021/acs.jpclett.2c00741. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The computer code for the calculations of this study will be made publicly available in the DeepQMC repository38 upon publication of the manuscript.