Skip to main content
[Preprint]. 2024 Sep 21:2024.09.17.613599. [Version 1] doi: 10.1101/2024.09.17.613599

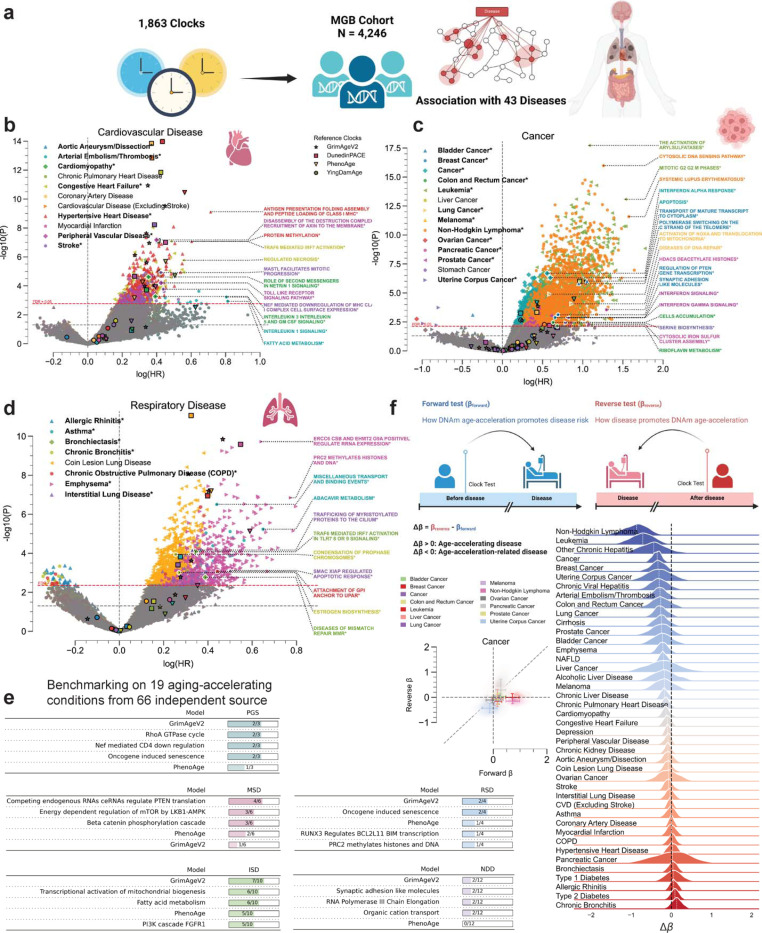
Figure 4. Ageome predicts disease risk and reveals bidirectional aging-disease relationships.

Figure 4.

(a) Schematic of the Ageome clock framework applied to the Mass General Brigham (MGB) cohort (N = 4,245) for disease risk prediction.

(b-d) Volcano plots showing the relationship between log(HR) and -log10(P) for Ageome clock predictions of (b) cardiovascular diseases, (c) cancers, and (d) respiratory diseases. Top two pathways for disease with FDR < 0.05 are labeled. Reference models are indicated by distinct markers with black borders: GrimAgeV2 (star), DunedinPACE (square), PhenoAge (triangle), and YingDamAge (circle). FDR threshold is set to 0.05, indicated by the dashed red line. The diseases that have Ageome measurements that outperform (either by significance or hazard ratio) reference models are bolded and indicated by an asterisk (*), as well as the outperforming pathways. Only the top 2 Ageome pathways (ranked by -log10(P) * log(HR)) with FDR < 0.05 are shown for each disease.

(e) Benchmarking analysis comparing Ageome clocks to GrimAgeV2 and PhenoAge across various disease categories using the ComputAgeBench framework. ISD: immune system diseases; MSD: musculoskeletal diseases; NDD: neurodegenerative diseases; PGS: progeroid syndromes; RSD: respiratory diseases. Panels for cardiovascular diseases and metabolic diseases are not shown as none of the clocks provide predictions for these conditions.

(f) Bidirectional analysis of aging-disease relationships. Schematic plot showing the logistics of forward (βForward) and reverse (βReverse) analysis. Scatter plot and 2D density plot (left) shows forward (X-axis) and reverse (Y-axis) effects for different cancers. Error bar shows the standard deviation of the forward and reverse effects across Ageome clock measurements. Delta age (Δβ) represents the difference between forward and reverse effects. The density plots show the distribution of Ageome clock Δβ for each disease, with the white dashed line annotating the median value. The black dashed line shows the line where Δβ = 0.