Interruptions in gene expression drive highly expressed operons to the leading strand of DNA replication

Abstract

In bacteria, most genes are on the leading strand of replication, a phenomenon attributed to collisions between the DNA and RNA polymerases. In Escherichia coli, these collisions slow the movement of the replication fork through actively transcribed genes only if they are coded on the lagging strand. For genes on both strands, however, these collisions sever nascent transcripts and interrupt gene expression. Based on these observations, we propose a new theory to explain strand bias: genes whose expression is important for fitness are selected to the leading strand because this reduces the duration of these interruptions. Our theory predicts that multi-gene operons, which are subject to longer interruptions, should be more strongly selected to the leading strand than singleton transcripts. We show that this is true even after controlling for the tendency for essential genes, which are strongly biased to the leading strand, to occur in operons. Our theory also predicts that other factors that are associated with strand bias should have stronger effects for genes that are in operons. We find that expression level and phylogenetic ubiquity are correlated with strand bias for both essential and non-essential genes, but only for genes in operons.

INTRODUCTION

In most bacterial genomes, a majority of genes are on the leading strand of DNA replication, so that transcription occurs in the same direction as replication (1). For genes on the lagging strand, DNA and RNA polymerases move in opposite directions, which creates head-on collisions that dramatically reduce the speed of the replication fork in Escherichia coli (2). For genes on the leading strand, collisions still occur because DNA polymerase moves much faster than RNA polymerase, but these co-directional collisions have little or no effect on the speed of the fork. Thus, Brewer proposed that strand bias results from selection to maintain the speed of the replication fork (3). Consistent with this theory, the phenomenon of strand bias was first identified for ribosomal DNA, ribosomal proteins, and other highly expressed genes which should experience frequent collisions and hence would slow down the fork if they were on the lagging strand (3,4).

This plausible and widely accepted theory was recently called into question by the finding that the tendency for genes to be on the leading strand is largely independent of expression level and instead depends on whether or not the gene is ‘essential’ (absolutely required for growth even in rich media) (5,6). Although the majority of highly expressed genes are found on the leading strand, Rocha and Danchin (5,6) found that only highly expressed genes that are also essential are strongly biased. Furthermore, they found that essential genes that are not highly expressed are also strongly biased, implying that essentiality and not high expression is the cause of strand bias. Importantly, these results established that the selection that drives strand bias depends on properties of the genes themselves rather than on how they affect the replication fork.

Why should essential genes be selected to the leading strand? Rocha and Danchin (5,6) proposed that head-on collisions (but not co-directional collisions) between DNA and RNA polymerases would remove RNA polymerase from the DNA template and produce truncated transcripts; translation of these truncated transcripts would then produce toxic truncated peptides (5). Truncated peptides from essential genes would be especially toxic, for example because they would disrupt the formation of essential complexes. However, RNA polymerases are dislodged by either types of collision in vivo (2), so truncated transcripts should arise irrespective of strand. In a more recent description of the theory, Rocha proposed that, for genes on the leading strand, the replication fork slows down until RNA polymerase terminates (7). However, the replication fork is not slowed by co-directional collisions with RNA polymerase, and the fork removes RNA polymerase instead of waiting behind it (2).

The toxic peptide hypothesis also requires that the tmRNA system, which releases ribosomes from truncated transcripts and also targets the truncated peptides for degradation, be saturated during replication (5). We feel that this assumption is speculative. Furthermore, because the ribosome often falls off from the transcripts on its own accord (8), truncated peptides normally occur at low levels, regardless of the replication fork's action on RNA polymerase. Indeed, in situations where tmRNA activity is essential for growth, its ability to free stalled ribosomes for future translation is required, but its tagging of truncated peptides for proteolysis is not required (9). Thus, there is little evidence for the existence of such toxic truncated peptides.

Another explanation for strand bias was recently given by Omont and Kepes (10). In their statistical–mechanical model, both head-on and co-directional collisions interrupt gene expression, and neither type affects the speed of the replication fork. Nevertheless, transcription units (TUs) on the lagging strand will experience more collisions because the new transcripts that initiate while the fork moves across the TU will soon collide with the fork, while for transcripts on the leading strand, the fork will race ahead of the RNA polymerases that initiate behind it.

Several observations bring Omont and Kepes' (10) conclusions into question. First, the DNA polymerase moves so much faster than the RNA polymerase (∼20 times faster) that the newly initiated transcripts will only increase the number of collisions on the lagging strand by 5% (7). In contrast, the replication fork can move an order of magnitude more slowly through a highly transcribed region if it is on the lagging strand (2). Second, to explain the selective basis for strand bias, Omont and Kepes (10) also invoked toxic truncated peptides resulting from these collisions. Third, they concluded that a higher number of truncated peptides should be produced for genes in operons because there are more collisions per operon. The number of truncated peptides per gene, however, should depend only on the number of collisions within that gene, and not on the total number for the transcript. Fourth, they predicted and found that multi-gene operons are more strongly biased toward the leading strand than single-gene transcripts. However, they did not consider whether this tendency might be explained by essentiality, as had been previously found for the strand bias of highly expressed genes (5). Indeed, essential genes are preferentially found in operons (11). Finally, their analysis of the strand bias of operons relied on operon predictions, which we will argue may themselves be biased to the leading strand.

In this paper, we propose and test a simple theory to explain the bias of genes to the leading strand of DNA. Our theory relies on empirical phenomena and does not require toxic truncated peptides. In our view, the collisions between RNA and DNA polymerases create interruptions in gene expression, and selection to minimize these interruptions can drive important genes to the leading strand. More specifically, because the replication fork moves more slowly through genes being transcribed on the lagging strand (2), deleterious interruptions last longer if the gene is on the lagging strand. To explain why essential genes are particularly biased toward the leading strand, we observe that, by definition, the complete removal of essential genes is far more deleterious to the cell than the removal of other genes. Hence, it seems likely that the partial removal of a gene via a brief interruption of its expression would also be particularly deleterious for essential genes.

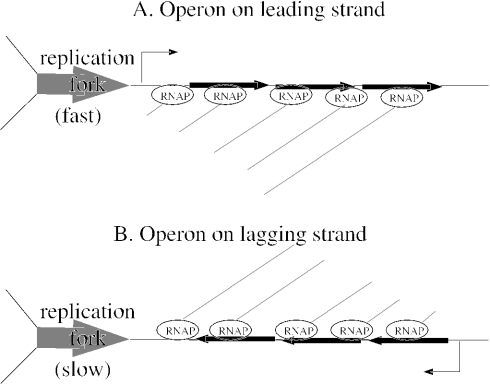
For genes in multi-gene operons, the effect of strand bias on interruptions will be particularly pronounced, as the interruptions last longer for genes in longer transcripts. To give a specific example of the interaction between transcript length, strand and the duration of the interruption, consider a gene of a typical length of 1 kb. If individually transcribed and on the leading strand, it would experience an interruption of ∼1 kb/(1 kb/s) = 1 s, where 1 kb/s is the speed of the fork. If this gene were on the lagging strand, the interruption might rise to 10 s or more, as co-directional collisions can slow the fork by an order of magnitude (2). If the gene were at the end of an operon with a typical length of 3 kb (3 genes), then the interruption would be three times longer, because the replication fork could interrupt RNA polymerase within the upstream genes as well as within the gene itself (see Figure 1). Thus, the interruptions would be 10 s if on the leading strand and 30 s if on the lagging strand, so the penalty for being on the lagging strand would be 27 additional seconds of interruption for the operon, compared to only 9 s for the individually transcribed gene.

Figure 1.

The replication fork creates the longest interruptions in gene expression for operons on the lagging strand. (A) For an operon on the leading strand, the replication fork interrupts expression of all genes in the operon as it moves through it. New transcripts initiate behind the fork (not shown) and resume the expression of the upstream genes in the operon first, so that the last (rightmost) gene experiences the longest interruption. (B) For operons on the lagging strand, the replication fork also interrupts expression of all genes. Expression of the operon cannot resume until the fork moves past the transcription start site, as new transcripts are destroyed by the fork. Expression of the last (leftmost) gene in the operon resumes latest. Because the fork is slowed by head-on collisions, the interruptions are longer than in (A), but in both cases, the RNA polymerases move much more slowly than the fork.

We argue that these interruptions in gene expression are deleterious because they perturb the cell and not because they prevent the production of adequate amounts of essential proteins. The proteins that were ‘lost’ (that would have been produced if not for the interruption) would likely be replaced due to homeostatic regulation, which would briefly increase the rate of transcription after the interruption ends. Alternatively, a slight permanent increase in the constitutive strength of the promoter could compensate for the lost expression. Instead of preventing the production of adequate amounts of protein, we argue that the brief interruptions in gene expression will alter the balance of cell growth. For structural components of the cell, such as ribosomal proteins or cell wall constituents, the entire cell growth process could be slightly delayed. For essential enzymes, which comprise most of the essential genes, the brief interruption will not stop growth but will still perturb the flux catalyzed by the enzyme. In either case, the effect on the cell should not depend on whether the gene is highly or lowly expressed, but rather on the importance of the gene's activity to the cell. Similarly, these interruptions temporarily reduce the expression of the gene regardless of the half-life of the encoded mRNA: mRNAs that would otherwise have been synthesized and translated into protein will be missing, even though mRNAs that were synthesized before the interruption began are still functioning.

The effect of these interruptions may seem slight, but the evidence indicates that the fitness effect of placing genes on the lagging strand is indeed slight. In naturally occurring bacteria, there are rare cases where strand bias is violated: even rDNA operons have been found on the lagging strand (12), and Pyrococcus furiosus has 55% of its genes on the lagging strand (7). Experimentally, deleterious effects have been observed for large chromosomal rearrangements in E.coli and in the Gram-positive bacterium Lactococcus lactis (3,13,14), but only for rearrangements near the origin and terminus. These rearrangements probably disrupt replication by moving strand-specific sites for the termination of DNA replication (13,15) or by imbalancing the two replication arms (14), rather than by creating additional collisions between DNA and RNA polymerases as originally supposed (3). (de Massy et al. (13) also reported non-specific effects of orientation on the fork's speed near the terminus, but they identified only two terminator sites, whereas six sites are now known (15); the four additional sites appear to explain those results.) In L.lactis, which has 81% of its genes on the leading strand, inversions within a chromosome arm of up to 370 kb—inversions that moved hundreds of genes from the leading strand to the lagging strand—had little or no effect on fitness, even in rich media, and were stable for 150 generations (14).

To test our theory, we first revisited the question of whether multi-gene operons are more biased than singleton transcripts. As mentioned above, a previous study neglected to test whether the apparent correlation between operons and strand bias could be explained by the known tendency of essential genes to occur in multi-gene operons. We controlled for essentiality by testing essential and non-essential genes separately, and found that multi-gene operons are biased toward the leading strand regardless of essentiality. We also argue below that operon predictions might be biased to the leading strand, so we verified these results with characterized operons in two well-studied species, Bacillus subtilis and E.coli.

To extend the analysis of the strand bias of operons to other prokaryotes, we developed a way to examine the strand bias of operons without making specific operon predictions. We relied on the observation that, across the prokaryotes, genes in operons tend to be separated by fewer base pairs than non-operon pairs (16,17). We confirmed that operons are biased to the leading strand in most prokaryotes, so that the proportion of same-strand pairs that are in operons is approximately the same on both strands. (This somewhat counter-intuitive statistical effect will be explained in Results.) This observation allowed us to develop a new method for estimating the total number of TUs in strand-biased genomes and hence to improve operon predictions (17).

Our theory also predicts that the factors that bias genes to the leading strand should have stronger effects for genes that are in multi-gene operons, as interruptions in gene expression are longer for such genes. We tested this prediction for two factors: expression level and the breadth of genomes that contain each gene. Highly expressed genes should experience more collisions between DNA and RNA polymerases and hence longer interruptions. The other property, which we call ‘phylogenetic ubiquity’, measures how strongly deletion of a particular gene is selected against in the natural environment, as compared to essentiality, which measures the importance of a gene in a single laboratory-controlled setting. For both expression level and phylogenetic ubiquity, we found that, after controlling for essentiality, genes in operons have higher scores if they are on the leading strand, whereas individually transcribed genes do not.

MATERIALS AND METHODS

Operon predictions

We use the term ‘operon bias’ to describe the excess of operons on the leading strand over and above what is expected from the excess of genes on the leading strand. To detect operon bias, we analyzed known operons in B.subtilis and E.coli K12 (18,19) as well as predicted operons in these organisms (17). Briefly, we predicted whether pairs of adjacent genes that are on the same strand are in the same operon, based on the intergenic distance between them, whether orthologs of the genes are near each other in other genomes, and their predicted functions. Both the predictions and the underlying features are available at http://www.microbesonline.org/operons. These operon predictions are over 80% accurate on pairs of genes in both organisms, based on databases of known operons and on analysis of microarray data. The accuracy of the prediction of whether a gene is in an operon or not is more difficult to assess, as the databases are heavily biased towards operons, and some genes are incorrectly described as not being in operons because of alternative transcripts that are missing from the databases (17,20). For E.coli, where over 1000 genes are in known operons, we considered two genes to be in the same operon if an operon had been observed experimentally, even if they were predicted to be transcribed separately. For both genomes, we assessed strand bias according to the experimentally determined origin and terminus of replication (21,22).

Simulation of intergenic distances

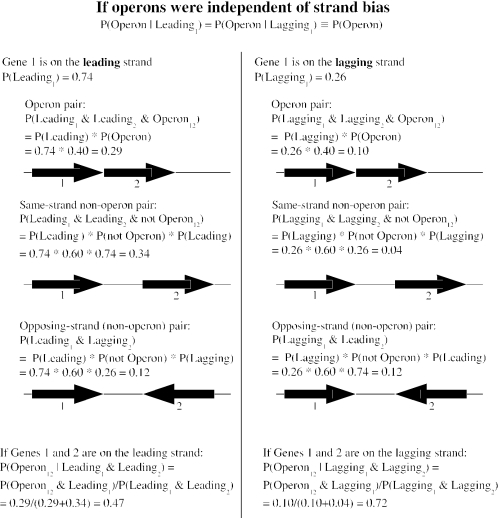
Because the distances between genes in operons tend to be smaller than the distances between other same-strand pairs (16), we examined the distribution of intergenic distances on both strands of B.subtilis. As explained in Results, if operons are not biased to the leading strand, then same-strand pairs on the leading strand should be less likely to be in operons than those on the lagging strand (see Figure 2) and should be, on average, farther apart. To estimate what this difference would be if operons were not biased, we performed simulations. We estimated the number of operon and non-operon pairs on each strand, and then sampled the appropriate number of times from the observed distances for known operon and non-operon pairs to give the simulated distances between pairs of genes on the leading and lagging strands. The number of operon and non-operon pairs on each strand can be derived from the total numbers of same-strand pairs on each strand (2601 and 532, respectively) and the proportion of same-strand pairs that are in operons for each strand. Under the assumption that operons are not biased, this proportion would be 38.3% for the leading strand and 64.1% for the lagging strand. These numbers can be derived from the observed pattern of strand bias and the proportion of same-strand pairs. Specifically, given the model in Figure 2 and the empirical observations that P(Leading) = 0.74 and P(Leading₂|Leading₁) = 0.83, we solved P(Leading₂|Leading₁) = P(Operon) + [1 − P(Operon)] · P(Leading) to give P(Operon) ≡ P(Operon|Leading₁) = P(Operon|Leading₂) = 0.316, P(Operon₁₂|Leading₁, Leading₂) = P(Operon₁₂|Leading₁)/P(Leading₂|Leading₁) = 0.383 and P(Operon₁₂|Lagging₁, Lagging₂) = P(Operon|Lagging₁)/P(Lagging₂|Lagging₁) = 0.641. The estimate of P(Operon) used for the simulations is lower than that used in Figure 2; this estimate is derived from the null hypothesis that operons are not biased and thus is appropriate for testing the null hypothesis, whereas the estimate in Figure 2 is derived from operon predictions and is more realistic and illustrative.

Figure 2.

If operons were independent of strand bias, then pairs of genes on the leading strand would be less likely to be in operons. We show the six probabilities for two adjacent genes to be in the same operon (or not) and on the same strand (or not), given that the first gene is on the leading strand (or not). The probabilities are derived from the null hypothesis that operons do not affect strand bias and from 74% of genes being on the leading strand of B.subtilis. The estimate is that 40% of genes are in an operon with their downstream gene from the output of our operon predictions (also for B.subtilis). The statistical effect arises from considering only same-strand pairs: if operons were independent of strand bias, then most lagging-strand pairs but only about half of leading-strand pairs would be in the same operon.

Genomes

To examine the relationship between strand bias and operons more broadly, we examined ∼200 complete annotated genomes from the MicrobesOnline database (23). We needed to assign genes to the leading and lagging strands, which in turn requires predicting the origin and terminus of replication. We used the GC skew method (24)—we plotted the cumulative GC skew (the number of guanines minus the number of cytosines) for windows of 2 kb, and within each chromosome, we identified the position of maximum cumulative skew, and predicted this to be the terminus. After rotating the plot so that the terminus is at the left-hand side, we predicted the position with minimum cumulative skew to be the origin. We subtracted the genome-wide average GC skew from each window before plotting the cumulative sum (25). Only chromosomes with strongly ‘v’-shaped plots were retained, and plasmids and linear chromosomes were excluded. Furthermore, it is possible for a majority of genes to be on the lagging strand, as in P.furiosus, whose origin has been identified experimentally (12). Because we are investigating the forces that drive genes to the leading strand in most chromosomes, we excluded five chromosomes which have a (slight) majority of genes on the lagging strand. We also required the preponderance of genes on the leading strand to be statistically significant (binomial test, P < 0.001; for comparison, the modest bias in the E.coli K12 chromosome gives P < 10⁻¹³). We were left with a dataset of 139 bacterial (and zero archaeal) chromosomes. To validate the predicted origins of replication, we compared them to clusters of putative dnaA binding sites [from Supplementary Table 1 of (25)]. Our predicted origin was correct to within 10 kb in 46 of 61 chromosomes; in the worst case, the discrepancy amounted to only 3.7% of the chromosome (for Nitrosomonas europaea ATCC 19718).

Conserved operons and orthologs

As a rough way to identify conserved operons in these genomes, we defined adjacent pairs of genes with conserved proximity as pairs whose orthologs were found within 5 kb in a distantly-related genome. Orthologs were defined as bidirectional best BLAST hits with 75% alignment coverage. Distantly-related genomes were identified by clustering together any pair of genomes for which >5% of convergently transcribed pairs of adjacent genes in one genome had orthologs within 5 kb in the other. Using this definition of conserved proximity, 79% of known E.coli operon pairs are conserved in a distant genome, but only 23% of known same-strand non-operon pairs are conserved. The corresponding analysis for B.subtilis gives 69% versus 23%, respectively.

Gene expression levels

To test the relationship between strand bias, operons and expression level, we used gene expression microarray data for B.subtilis and E.coli from the Stanford Microarray Database (SMD) (26), with 78 arrays each for B.subtilis and E.coli. We used the average foreground intensity across arrays and across both red and green channels as our estimate of expression level. We used intensities rather than more direct measures of expression levels, which can be obtained from microarray experiments where an mRNA sample is compared to genomic DNA, because none of the B.subtilis experiments, and only a few of the E.coli experiments, were of this type. Within these E.coli ‘genomic control’ experiments, the average across replicates of the intensity in the mRNA channel was highly correlated with the average log-ratio between the mRNA and genomic DNA channels (the Spearman rank correlation was 0.84). This confirms that intensities give reasonable estimates of mRNA expression levels. For each gene, we used only arrays with high-quality spots (spots for which SMD provided an estimate of normalized log-ratios).

Phylogenetic ubiquity

We also tested the relationship between strand bias, operons and phylogenetic ubiquity. We used phylogenetic ubiquity as a broad indicator of each gene's importance to the cell. To compute the phylogenetic ubiquity, we first formed clusters of genomes with similar gene content. We linked two genomes together if >50% of genes in one genome had orthologs in the other, and two genomes were placed in the same cluster if there was a path connecting them. From 127 genomes in an earlier version of the MicrobesOnline database (23), we derived 75 clusters (see Supplementary File 1). We defined the phylogenetic ubiquity of each gene as the number of clusters of genomes that contained an ortholog for that gene (not including the cluster of the genome containing the gene itself).

RESULTS

Known and predicted operons are biased

In our model of strand bias, genes in operons experience longer interruptions in gene expression than do singleton transcripts, and therefore will be more strongly selected to the leading strand. We first investigated the bias of experimentally characterized operons in B.subtilis and E.coli. B.subtilis has most of its genes on the leading strand, while in E.coli only essential genes are strongly biased. Because essential genes tend to be in operons (11), we examined essential and non-essential genes separately. We used lists of essential genes from genome-wide screens (27,28), and excluded non-essential genes predicted to be in an operon with an essential gene, as these will also show strand bias (5).

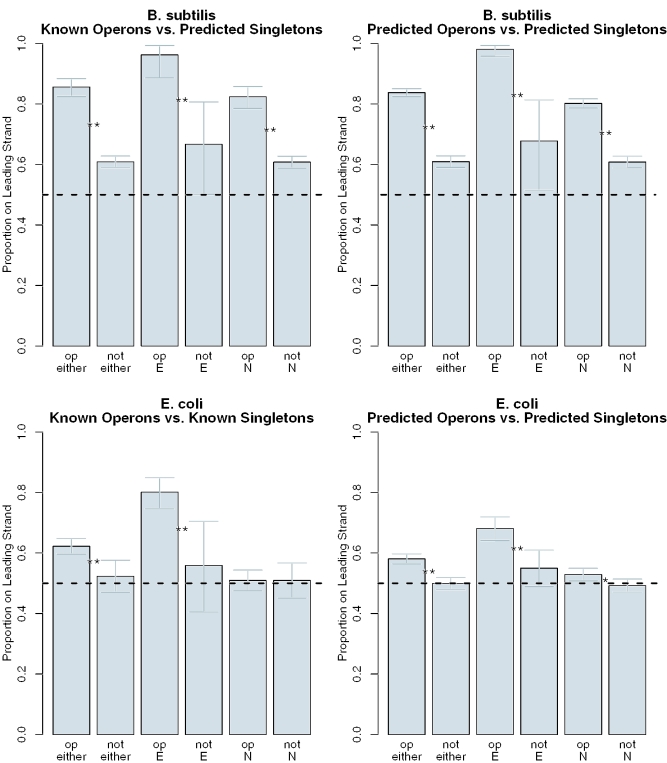
In B.subtilis, both essential and non-essential genes are significantly more biased to the leading strand if they are in known operons than if they are predicted singletons (Figure 3). Unfortunately, our database of known operons in B.subtilis (18) does not include singleton transcripts, so we were unable to compare known operons to known singletons. In E.coli, however, where such data is available, essential genes are significantly more likely to occur on the leading strand if they are part of multi-gene operons than if they are known singletons (Figure 3). Non-essential E.coli genes are so weakly biased in E.coli that there is no difference between the two types of genes. We also analyzed operon predictions for both organisms, and found similar results: in both organisms, both essential and non-essential genes are significantly more biased if they are in predicted operons (Figure 3). We concluded that operons in E.coli and B.subtilis are biased, i.e. operons are over-represented on the leading strand relative to single-gene transcripts.

Figure 3.

Strand bias of operons and individually transcribed genes in B.subtilis (above) and E.coli (below). We asked whether genes in multi-gene operons (‘op’) showed greater bias than genes not in operons (‘not’). We examined essential (‘E’) and non-essential (‘N’) genes separately and also show the combined results (‘either’). We analyzed both operon predictions (left) and known operons (right). Error bars show 95% confidence intervals for the proportion of genes in each category on the leading strand (from the binomial test). Significant differences between operons and singletons are marked with ‘**’ (P < 0.005, Fisher's exact test) or ‘*’ (P < 0.05, Fisher's exact test). The horizontal dashed line at 0.5 indicates equal proportions of genes on the leading and lagging strands, or no bias.

While using operon predictions might allow us to extend our analysis to a much larger set of genomes, there is a potential artifact associated with using predicted rather than known operons. Most methods for predicting operons, including ours and those previously used to study operon bias (10), examine adjacent pairs of genes on the same strand and try to predict whether each pair is in an operon (16,17,20). Because operon predictions are only 80–90% accurate, operon predictions are a mixture of true operons and false-positives. The simplest assumption is that false-positives would be randomly selected from the candidate non-operon same-strand pairs. In strand-biased genomes, same-strand pairs (and therefore false-positives) will usually be found on the leading strand.

Intergenic distances and the strand bias of operons

To avoid the problem of false-positive operon predictions, and to extend our analysis to bacteria where databases of known operons are not available, we examined the distances between pairs of adjacent genes on the same strand. Across the prokaryotes, adjacent genes tend to be much closer together if they are in the same operon (16). Thus, if operons are biased to the leading strand, then genes on the lagging strand should be farther apart.

However, there is a statistical effect that works in the opposite direction. This effect results from considering only the same-strand pairs. Regardless of any strand bias of operons, genes on the lagging strand will tend to be adjacent to genes on the leading strand, simply because most genes are on the leading strand. Thus, when two or more consecutive genes are observed on the lagging strand, it becomes likely that those genes are in an operon. A more rigorous derivation of this statistical effect, in the context of B.subtilis, is shown in Figure 2. Because lagging-strand pairs are more likely to be in operons than leading-strand pairs, they would tend to be closer together.

What is the relative contribution of these opposing factors? Surprisingly, in B.subtilis these two effects balance each other out almost precisely: the two distributions of distances—between adjacent pairs on the leading and lagging strands—are statistically indistinguishable (Kolmogorov–Smirnov test, D = 0.03, P > 0.5; D is a non-parametric measure of similarity and ranges from 0 for identical distributions to 1 for non-overlapping distributions). For comparison, distances within known operon and non-operon pairs follow very different distributions (D = 0.73, P < 10⁻¹⁵). We performed simulations to determine what we should expect if B.subtilis operons were not biased (see Methods). In 100 simulations, the difference between intergenic distances on the two strands was consistently and highly statistically significant (D = 0.16–0.23, all P < 10⁻⁸). Furthermore, this difference remained significant over a range of settings for the key parameter: the fraction of genes in operons. This confirms that, in B.subtilis, operons are significantly biased.

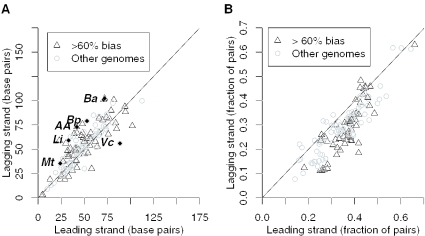
We then examined the distributions of intergenic distances on the leading and lagging strands of 139 completely sequenced bacterial chromosomes (Supplementary Table 1). As shown in Figure 4A, intergenic distances are similar on both strands in most bacteria, whether they have strong strand bias or not. To identify exceptions to this trend, we used the Kolmogorov–Smirnov test to find chromosomes with differing distributions of distances, and we then used the false discovery rate (29) to correct for multiple hypothesis testing. At a false discovery rate of 5%, we identified seven chromosomes with significant differences between strands (see Figure 4A and legend). Except for Acinetobacter ADP1, all of the chromosomes are from pathogens. Two of them are from closely related Bacillus anthracis strains that have numerous pseudogenes, including pseudogenes within ancestral operons (17). This may explain why the median spacing between adjacent genes in these genomes is relatively large, but does not seem to explain the difference between strands, because pseudogenes [as identified in (23)] are about as biased as protein-coding genes (P > 0.05, Fisher's exact test). Despite these exceptions, distributions of intergenic distances are surprisingly similar between strands, indicating a balance between the bias of operons and the statistical effect discussed above.

Figure 4.

Across 139 chromosomes from 130 bacteria, adjacent pairs of genes on the leading and lagging strands are separated by similar distances, but pairs on the leading strand are more conserved. (A) The median distance between pairs on the leading strand (x-axis) and the lagging strand (y-axis). (B) The proportion of pairs that are conserved within 5 kb in a distant genome, on both strands (same axes). The lines show x = y. In (A), a few chromosomes do have significantly different distributions of distances on the two strands (false discovery rate < 0.05) and are indicated with labels and filled diamonds: ‘Ba’, Bacillus anthracis Ames strain and Ames ancestor strain; ‘Bp’, Burkholderia pseudomallei K96243 chromosome 2; ‘AA’, Acinetobacter sp. ADP1; ‘Li’, Leptospira interrogans serovar Copenhageni strain Fiocruz L1-130 chromosome 1; ‘Mt’, Mycobacterium tuberculosis H37Rv; and ‘Vc’, Vibrio cholerae chromosome 2. In (B), none of the chromosomes have significantly greater conservation of pairs on the lagging strand (the points above the line are not significantly different from equality, all P > 0.05, Fisher's exact test).

The remarkable balance between operon bias and the statistical effect can be used to estimate the total number of operons in strand-biased genomes and hence to improve operon predictions (17). Briefly, the balance can be formalized as an assumption that P(Operon₁₂|Leading₁, Leading₂) = P(Operon₁₂|Lagging₁, Lagging₂). Given the proportion of genes on the leading strand, the frequency of same-strand pairs, and formulas for the number of operon and non-operon pairs on each strand analogous to those shown in Figure 2, we can solve for P(Operon₁₂|Leading₁, Leading₂) (17).

Conserved operons are more biased

To confirm that the similarity of distance distributions between strands arises from the bias of operons, we investigated adjacent pairs of genes that tend to occur in close proximity across distantly related genomes. These pairs reflect conserved operon structure (17,20). As shown in Figure 4B, the fraction of conserved pairs is greater on the leading strand for most chromosomes. In general, the bias of conserved operons is especially strong in genomes with strong overall bias. There are some chromosomes where leading-strand pairs are less likely to be conserved, but none of these are statistically significant (all P > 0.05, Fisher's exact test). In contrast, the greater tendency for pairs to be conserved if they are on the leading strand is significant (P > 0.05) in 126 of the 139 chromosomes that we analyzed.

Furthermore, bias is stronger for conserved pairs than for operons overall. In most chromosomes, operon pairs are equally prevalent on both strands, as indicated by the similarity of intergenic distance distributions (Figure 4A), but conserved operon pairs are preferentially found on the leading strand (Figure 4B). In B.subtilis, we tested whether this effect was due to the tendency for conserved operons to contain essential genes. We found that conserved operon pairs containing only non-essential genes were significantly more biased to the leading strand than were other adjacent pairs of genes (86% versus 77%, P < 0.005, Fisher's exact test). We concluded that operons are generally biased to the leading strand, consistent with previous analyses (10), and that conserved operons are particularly biased.

Higher expression levels and phylogenetic ubiquity for operons on the leading strand

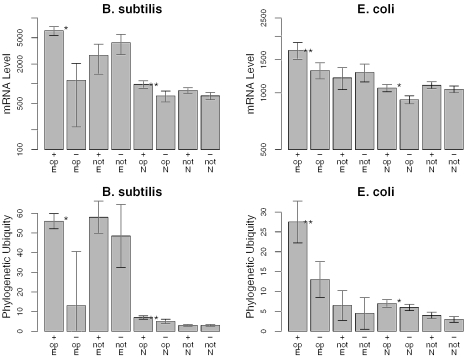
Given that the length of interruptions in gene expression is related to the length of each transcript, our theory predicts that some factors that weakly affect bias might be magnified in effect for longer transcripts. We first revisited the question of whether gene expression level affects bias, using genome-wide microarray data from SMD (26). Although no correlation between expression level and strand bias was observed in a previous study that controlled for essentiality (5,6), we observed a clear effect for genes in operons in both B.subtilis and E.coli (Figure 5). Importantly, this effect was seen for both essential and non-essential genes and was not seen for singletons.

Figure 5.

After controlling for essentiality, genes in predicted operons are more highly expressed and more phylogenetically ubiquitous if they are on the leading strand. We show the median of expression level (top) and phylogenetic ubiquity (bottom) for essential (‘E’) or non-essential (‘N’) genes on the leading (‘+’) or lagging (‘−’) strand predicted to be in operons (‘op’) or not, from B.subtilis (left) and E.coli (right). For each group of genes, the gray bars show the median and the error bars indicate the 90% confidence interval of the median. Significant differences between genes on the leading and lagging strands are marked with ‘**’ (P < 0.005, Wilcoxon rank sum test) or ‘*’ (P < 0.05). As in Figure 3, non-essential genes in predicted operons with essential genes are not included.

We next examined the ‘phylogenetic ubiquity’ of genes—the number of distinct taxa that each gene is conserved across. This measure is logically and empirically correlated to essentiality (27,28), but is a broader measure of a gene's ‘importance’ to the cell, as it measures selection against deletion (or replacement) in the natural environment, while essentiality applies to a particular laboratory-controlled condition. As we found for expression level, genes on the leading strand of B.subtilis and E.coli are significantly more phylogenetically ubiquitous, regardless of essentiality, but only if they are in operons (Figure 5).

Finally, we asked whether the interactions between operon length and both expression level and phylogenetic ubiquity were significant predictors of whether TUs were on the leading or lagging strand. We performed generalized ANOVA on a logistic regression model. (We used logistic regression because the variable being predicted—whether each TU is on the leading or the lagging strand—is binary rather than continuous.) We built separate models for B.subtilis and E.coli, and separate models for phylogenetic ubiquity and expression level. Unlike linear ANOVA, significance estimates in generalized ANOVA depend on the order in which variables are added to the model. We began with essentiality (whether the TU contained an essential gene or not), which is the strongest single predictor (data not shown) and then added operon size (the number of genes in the TU), either expression level or ubiquity (we used the average log-level of expression within the operon, or the maximum of phylogenetic ubiquity), and finally the interaction effect between that variable and operon size. For both B.subtilis and E.coli, essentiality and operon size were highly significant predictors of being on the leading strand (all P < 0.05). For B.subtilis, after including essentiality and operon size in the model, adding expression level and then the interaction effect of expression and operon size significantly improved the fit (both P < 0.05), while for E.coli, no significant effects were seen (both P > 0.1). Similarly, for phylogenetic ubiquity, significant effects were found for the interaction effect within B.subtilis (both P < 0.05) but not in E.coli. Overall, these analyses confirmed a statistically significant interaction effect between strand bias, operon size, and both phylogenetic ubiquity and expression level in B.subtilis but not in the weakly biased genome of E.coli.

DISCUSSION

We have confirmed that operons are biased to the leading strand, as predicted by our interruption theory. We have extended previous observations (10) by controlling for essentiality, by testing known operons, and by developing a new test for the strand bias of operons that is not affected by the potential bias of operon predictions and by applying this test to many genomes. We found (i) that operons are biased to the leading strand in most prokaryotes, (ii) that conserved operons are particularly biased and (iii) that essentiality does not account for these effects.

The interruption theory is also supported by our finding that genes in operons on the leading strand are (i) more highly expressed and (ii) more phylogenetically ubiquitous than genes in operons on the lagging strand. This effect was not observed for singletons and remained after controlling for essentiality. In our view, the effect of expression level arises because RNA polymerase will be more densely packed on highly expressed genes, and the slow-down of the replication fork likely depends on the rate of head-on collisions with RNA polymerase. Thus, the increased duration of interruption for genes on the lagging strand will be proportional to the product of transcript length and expression level, which would explain why expression level is correlated with bias for operons in particular. Second, assuming that phylogenetic ubiquity reflects the strength of selection against deleting a gene, a similar relationship between phylogenetic ubiquity, transcript length, and strand bias results from a total fitness cost given by the product of the interruption's duration and the fitness cost to the cell per unit time of interruption.

Our results also confirm that expression level is not a major cause of strand bias, but we did find a tendency in both B.subtilis and E.coli for both essential and non-essential genes to be more highly expressed if they were on the leading strand. This finding is contrary to the previous results that used a subset of highly expressed genes or used codon usage as a proxy for expression level (5,6) instead of analyzing genome-wide expression data. However, the effect was significant only for genes in operons (Figure 5), and expression level was not as strong a predictor of strand bias as essentiality in either species (generalized ANOVA; data not shown). Thus, the pattern remains markedly different from what one would expect given the traditional theory (3) that strand bias is driven by selection on the speed of the replication fork.

Overall, we argue that the evidence is most consistent with strand bias serving to reduce interruptions in gene expression during replication. However, significant gaps remain in our understanding of coding strand bias. First, it is not known why head-on collisions slow down the replication fork. Topological differences between head-on and codirectional collisions provide one possible explanation (30). It is also not clear how much head-on collisions slow down the replication fork. For an rDNA operon in E.coli that has been moved to the lagging strand, the fork generally takes >6 min to move 5.4 kb (2), which implies that it is moving <1 kb/min. At over one minute per kilobase, it would take over a day for the replication fork to move from origin to terminus! However, rDNA operons are much more highly expressed than the typical gene, so they probably experience much more frequent collisions and have a much stronger effect on the fork. The modest overall bias of both genes and transcription in E.coli suggests that for most genes, the effect is small: only 54% of genes are on the leading strand, and from microarray data (26) we estimate that only 57% of transcription is from the leading strand.

Second, our understanding of how collisions with the replication fork affect RNA polymerase is largely based on a single study of an rDNA operon in E.coli (2). As rDNA operons are unusually highly expressed and because the RNA polymerase acquires an additional regulatory subunit while transcribing these operons, rDNA operons could be atypical. Another limitation of our knowledge on this topic is the lack of relevant data from organisms other than E.coli. For example, in B.subtilis and its relatives, which have particularly strong strand bias and a distinct DNA polymerase for synthesizing the lagging strand (1), the effects of collisions might be different. Although experimental results are available for T4 and Φ29 DNA polymerases, which do not remove RNA polymerase from the DNA when collisions occur (31–33), we argue that these findings are not relevant to bacterial strand bias. Neither of the virus has a defined origin of replication, and hence neither of the virus can use strand bias to avoid head-on collisions. Thus, this capability may be an alternative adaptation to the problem of head-on collisions (3,5).

Third, as discussed in Introduction, the deleterious effect of placing genes on the lagging strand appears to be slight. Without a measurable phenotype for placing genes on the lagging strand, it is difficult to test the various theories of strand bias directly. B.subtilis and its relatives, including L.lactis, have particularly strong bias, so these organisms might be most suitable for such experiments. A measurable fitness defect might not be required—research on codon usage, which also involves small selective effects, has progressed by measuring the relationship between codon usage and tRNA levels, and the effect of codon choice on translation elongation, without measuring the fitness effects directly.

Fourth, the total genome-wide bias does not depend on the frequency of DNA replication or on growth rate (1,6). This is surprising because strand bias is weakly selected, and therefore the penalty for placing a gene on the lagging strand must be very small, such as a short delay in growth that occurs once per replication. For rapidly growing bacteria with short generation times, this penalty will take up a larger fraction of the generation time, and so the selective pressure to place genes on the leading strand should be stronger. Because of this, it has been argued that the presence of strand bias in slowly growing bacteria reflects a lethal effect of placing genes on the lagging strand (1,6), but this is contradicted by the weak selection for strand bias discussed above.

Finally, we observe that in B.subtilis, 61% of non-essential genes predicted not to be in operons are on the leading strand. As these genes are not significantly more highly expressed or phylogenetically ubiquitous if they are on the leading strand, other causes of coding strand bias may remain to be discovered.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.