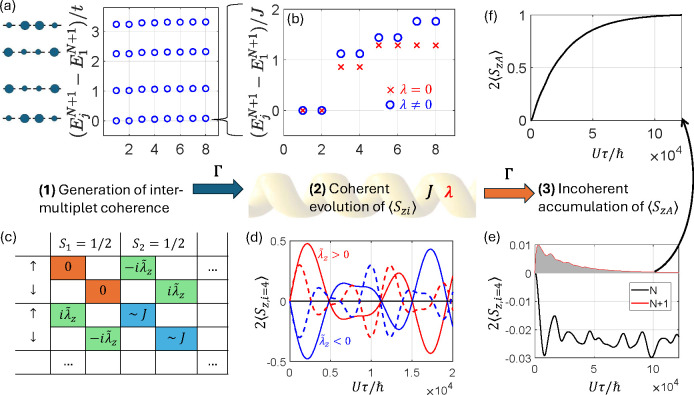
Figure 2.

Spin polarization mechanism. (a) Lowest-energy many-body states |ψ^N+1_j⟩ (j = 1, ..., 32) within the (N + 1)-electron subspace. On the left, a sketch of the charge distribution of the (N + 1) = 5 delocalized electrons on χ, calculated as the expectation value of n_i. (b) Zoom on the lowest energy block of the (N + 1)-electron subspace. (c) Scheme of nonzero populations (red and blue) and coherences (green) in the density matrix generated by the jump operator X_D from D to χ and corresponding matrix elements of the Hamiltonian (symbols), explicitly shown for the two lowest energy doublets of panel (b) with 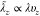. In this panel, to highlight the effect of SOC, we use the eigenbasis of H without SOC (i.e., λ = 0). (d) Time evolution of 2⟨S_z,i=4⟩ for an initial state prepared into X_Dρ(0)X^†_D (with population only in the lowest energy block of Figure 2-(a), i.e. |ψ^N+1_j⟩, j = 1, ..., 8) and using t/U = 0.0125, λ_z/U = 0.0005. With the basis used in panel (c), the amplitude of the oscillations is proportional the real part of intermultiplet coherences. 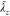Results for the two enantiomers (corresponding to opposite ) are represented by different colors, while dashed lines are obtained by halving correlations (i.e., using t/U = 0.025, λ_z/U = 0.001). (e) Full time evolution of 2⟨S_z,i=4⟩ including both coherent and incoherent dynamics in eq 2 and separated into contributions of states with either N or N + 1 electrons on χ. The latter is proportional to the derivative of S_zA accumulated on the acceptor (f), which can therefore be obtained from the shaded area in (e).