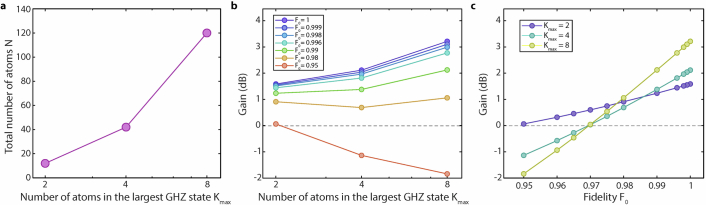
Extended Data Fig. 7. Projected metrological gain.

a, Total number of atoms N required as a function of the number of atoms in the largest GHZ state used in the protocol proposed in ref. ⁴. Efficient implementation requires n₀ copies of each GHZ state with 2^j atoms, j = 0, 1, …M − 1, where the largest GHZ state contains K_max = 2^M−1 atoms, and N = n₀(2^M − 1). The number of copies for K_max = 2, 4, 8 are n₀ = 6, 8, 9 respectively. b, Projected metrological gain for various effective fidelities per qubit F₀, as a function of the number of atoms in the largest GHZ state, K_max. We assume the contrast C of the parity oscillations for a K-atom GHZ state to scale as $C\left(K\right)=F_0^K$. c, Projected metrological gain as a function of effective fidelity per qubit F₀, for maximum GHZ size K_max = 2, 4, 8. We see that the effect of finite fidelity is more prominent for states with larger maximum GHZ sizes, causing the gain to decrease steeply with decreasing fidelity.