Individualized decision making in on-scene resuscitation time for out-of-hospital cardiac arrest using reinforcement learning

Abstract

On-scene resuscitation time is associated with out-of-hospital cardiac arrest (OHCA) outcomes. We developed and validated reinforcement learning models for individualized on-scene resuscitation times, leveraging nationwide Korean data. Adult OHCA patients with a medical cause of arrest were included (N = 73,905). The optimal policy was derived from conservative Q-learning to maximize survival. The on-scene return of spontaneous circulation hazard rates estimated from the Random Survival Forest were used as intermediate rewards to handle sparse rewards, while patients’ historical survival was reflected in the terminal rewards. The optimal policy increased the survival to hospital discharge rate from 9.6% to 12.5% (95% CI: 12.2–12.8) and the good neurological recovery rate from 5.4% to 7.5% (95% CI: 7.3–7.7). The recommended maximum on-scene resuscitation times for patients demonstrated a bimodal distribution, varying with patient, emergency medical services, and OHCA characteristics. Our survival analysis-based approach generates explainable rewards, reducing subjectivity in reinforcement learning.

Introduction

Out-of-hospital cardiac arrest (OHCA) is a global leading cause of death characterized by a high incidence (62.3 per 100,000 person-years) and low survival rate (<10%)^1,2. The outcomes of patients with OHCA depend on multiple factors, including patient characteristics, bystander cardiopulmonary resuscitation (CPR), and prehospital resuscitation by emergency medical services (EMS)^3–5. The duration of prehospital resuscitation efforts on the scene, known as on-scene resuscitation time, is also associated with the outcomes of OHCA patients, albeit with mixed results⁶. Although some studies suggested that the “scoop-and-run” strategy, advocating for early intra-arrest transport, leads to better survival^7,8, others indicated that extended on-scene resuscitation until return of spontaneous circulation (ROSC), known as “stay-and-play,” increases survival chances compared to intra-arrest transport⁹.

The rationale behind determining the optimal on-scene resuscitation time encompasses several considerations. On one hand, the quality of on-scene chest compressions is higher compared to that of compressions performed in a moving ambulance during intra-arrest transport¹⁰. Performing extended on-scene resuscitation is also associated with a higher rate of prehospital ROSC^9,11. On the other hand, early intra-arrest transport to the emergency department (ED) facilitates earlier provision of high-quality advanced life support (ALS), which is particularly important in areas where EMS is limited to providing basic life support (BLS)¹². Additionally, early intra-arrest transport can enable timely access to hospital resources, including extracorporeal cardiopulmonary resuscitation (ECPR), which can potentially improve patient outcomes^7,13,14.

The EMS guidelines for initiating transport for patients with OHCA vary by country, reflecting differences in EMS capabilities. In many Asian countries, the “scoop-and-run” strategy is advocated because the ALS system is less established¹². For instance, Korean guidelines recommend considering transportation if ROSC is not achieved after 6 min for BLS teams and 10 min for ALS teams during on-scene resuscitation¹⁵. In contrast, the “stay-and-play” strategy is predominantly adopted in Western countries with ALS EMS systems⁶. Additionally, while termination of resuscitation (TOR) is typically not performed in Korea unless there are signs of irreversible death, such as rigor mortis, it is often performed after prolonged on-scene resuscitation in ALS systems with dispatched physicians. Despite these differences, both EMS strategies are fundamentally population-based approaches.

While previous studies have identified a “one-size-fits-all” optimal on-scene resuscitation time, few have attempted to develop personalized approaches. One study developed models for predicting on-scene ROSC and conducted a simulation analysis to explore how these models could be used to enhance survival¹³. However, the simulation was based on simplistic assumptions, positing that the probability of survival decreases linearly over time at an empirically set rate. Another study employed deep learning to predict the outcomes of patients with OHCA, discovering that shorter on-scene times correlated with favorable outcomes¹⁶. Nevertheless, the research did not address “resuscitation time bias”, a phenomenon where extended durations of resuscitation, suggestive of unsuccessful initial resuscitative efforts, are linked to inferior outcomes^9,17.

With recent advances in reinforcement learning techniques, efforts to develop personalized treatment strategies have emerged within the medical domain. Reinforcement learning was utilized to optimize the dose of intravenous fluids and vasopressors for treatment of sepsis¹⁸. Deep Q-learning, where a neural network learns the value of actions in specific states, was used to develop a model to reduce cardiorespiratory instability by choosing actions between mechanical and manual ventilation¹⁹. These studies demonstrated that sequential decisions can be optimized using reinforcement learning to improve patient outcomes.

Sparse actions and rewards are common challenges in reinforcement learning within the medical domain, potentially leading to convergence issues^20,21. While reward-shaping methods like curiosity-driven exploration have been introduced, a clearer definition of rewards is often required from an offline reinforcement learning perspective²². Previous studies have mainly relied on empirically designed rewards for reinforcement learning, which may introduce subjectivity and bias in assigning reward values²³. If the reward shaping process could be grounded in data-driven evidence from domain knowledge, it would lead to more explainable and less biased policies.

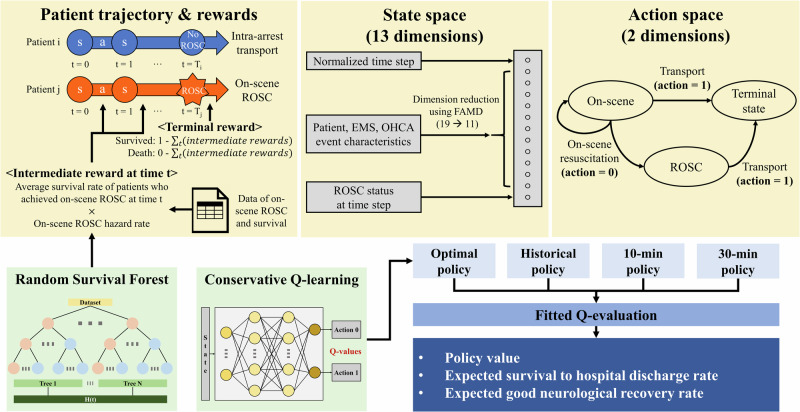
Therefore, we aimed to develop and validate a reinforcement learning model that uses knowledge-based, data-driven rewards to enable individualized decision-making in determining on-scene resuscitation times for patients with OHCA (Fig. 1). We hypothesized that the optimal on-scene resuscitation time varies among individuals and that employing a tailored decision-making approach would improve survival outcomes.

Fig. 1. Overall study concept diagram.

The development and evaluation process of the reinforcement learning models is outlined. A patient’s status at each time step (every 2 min) was modeled as the state, and the decision to continue on-scene resuscitation or initiate transport was considered the action. The on-scene ROSC hazard rate of each individual at each time step was used to derive the intermediate rewards and the actual survival to hospital discharge result of each patient was reflected in the terminal reward. The policies were evaluated using fitted Q-evaluation. s state, a action, ROSC return of spontaneous circulation, EMS emergency medical services, OHCA out-of-hospital cardiac arrest, FAMD Factor Analysis of Mixed Data.

Results

Descriptive analysis

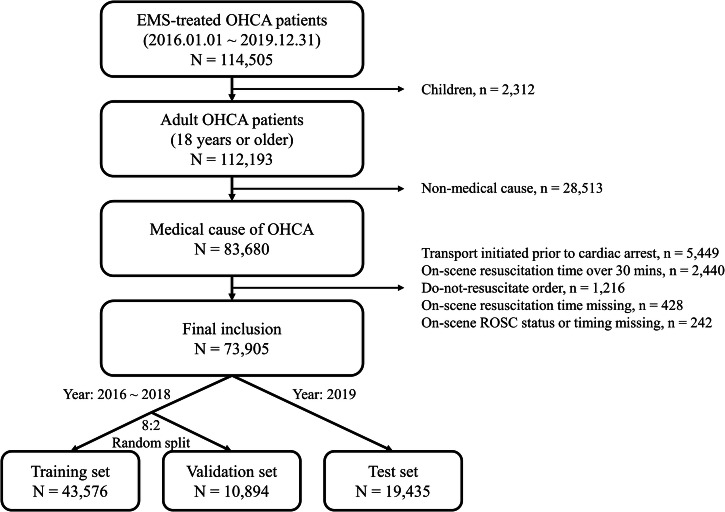
Among the 114,505 EMS-treated OHCA patients in the nationwide Korean OHCA registry (KOHCAR) during the study period, 73,905 patients (63.2% male), with a median age of 73 (interquartile range [IQR]: 60–82), were included in the analysis (Fig. 2). The training, validation, and test sets comprised 43,576, 10,894, and 19,435 patients, respectively. The median on-scene resuscitation time was 13 (IQR: 9–17) minutes in the training and validation sets, and 14 (IQR: 10–17) minutes in the test set. The proportion of patients with on-scene ROSC ranged from 9.0% to 10.1%. Survival to hospital discharge rates ranged from 9.5% to 9.6%, and the proportion of patients with favorable neurological outcomes ranged from 4.9% to 5.4% (Table 1).

Fig. 2. Study data flowchart.

Adult EMS-treated OHCA patients with a medical cause of arrest who did not meet any exclusion criteria were included in this study. A total of 73,905 patients were divided into training (N = 43,576), validation (N = 10,894), and test (N = 19,435) sets. EMS emergency medical services, OHCA out-of-hospital cardiac arrest, ROSC return of spontaneous circulation.

Table 1.

Characteristics of patients in the training, validation and test sets

	Total	Training set	Validation set	Test set
Total	73,905	43,576	10,894	19,435
Age, years	73 (60–82)	73 (59–81)	73 (60–82)	74 (60–82)
Sex, male	46,720 (63.2)	27,524 (63.2)	6846 (62.8)	12,350 (63.5)
Diabetes mellitus	16,850 (22.8)	9765 (22.4)	2442 (22.4)	4643 (23.9)
Hypertension	25,804 (34.9)	14,924 (34.2)	3725 (34.2)	7155 (36.8)
Heart disease	13,147 (17.8)	7478 (17.2)	1869 (17.2)	3800 (19.6)
Time of day, daytime (6AM-6PM)	46,694 (63.2)	27,489 (63.1)	6815 (62.6)	12,390 (63.8)
Region, urban	63,892 (86.5)	37,697 (86.5)	9407 (86.4)	16,788 (86.4)
ECPR-capable district	38,615 (52.2)	22,803 (52.3)	5723 (52.5)	10,089 (51.9)
Presumed cardiac cause	70,288 (95.1)	41,408 (95.0)	10,379 (95.3)	18,501 (95.2)
Place of arrest
Public	12,390 (16.8)	7330 (16.8)	1793 (16.5)	3267 (16.8)
Non-public	61,507 (83.2)	36,239 (83.2)	9100 (83.5)	16,168 (83.2)
Missing	8 (0.0)	7 (0.0)	1 (0.0)	0 (0.0)
Witnessed status
EMS witnessed	1754 (2.4)	917 (2.1)	218 (2.0)	619 (3.2)
Bystander witnessed	44,075 (59.6)	26,512 (60.8)	6604 (60.6)	10,959 (56.4)
Unwitnessed	27,727 (37.5)	15,892 (36.5)	4015 (36.9)	7820 (40.2)
Missing	349 (0.5)	255 (0.6)	57 (0.5)	37 (0.2)
Bystander CPR
Dispatcher-assisted	33,569 (45.4)	19,506 (44.8)	4818 (44.2)	9245 (47.6)
Unassisted	15,437 (20.9)	9295 (21.3)	2343 (21.5)	3799 (19.5)
No CPR	23,764 (32.2)	14,037 (32.2)	3565 (32.7)	6162 (31.7)
Missing	1135 (1.5)	738 (1.7)	168 (1.5)	229 (1.2)
Bystander AED use
Yes	3191 (4.3)	1938 (4.4)	465 (4.3)	788 (4.1)
No	70,160 (94.9)	41,341 (94.9)	10,347 (95.0)	18,472 (95.0)
Missing	554 (0.7)	297 (0.7)	82 (0.8)	175 (0.9)
Initial rhythm
Shockable	12,524 (16.9)	7512 (17.2)	1838 (16.9)	3174 (16.3)
Non-shockable	61,123 (82.7)	35,882 (82.3)	9007 (82.7)	16,234 (83.5)
Missing	258 (0.3)	182 (0.4)	49 (0.4)	27 (0.1)
EMS team level
Advanced	70,855 (95.9)	41,405 (95.0)	10,347 (95.0)	19,103 (98.3)
Basic	3050 (4.1)	2171 (5.0)	547 (5.0)	332 (1.7)
Prehospital mechanical CPR	10,330 (14.0)	4589 (10.5)	1188 (10.9)	4553 (23.4)
RTI, min	7 (5–9)	7 (5–9)	7 (5–9)	7 (5–9)
On-scene resuscitation time, min	13 (10–17)	13 (9–17)	13 (9–17)	14 (10–17)
TTI, min	6 (4–10)	6 (4–10)	6 (4–10)	6 (4–10)
Prehospital airway
Endotracheal intubation	5989 (8.1)	3742 (8.6)	906 (8.3)	1341 (6.9)
Supraglottic airway	48,994 (66.3)	27,585 (63.3)	6836 (62.8)	14,573 (75.0)
No	18,922 (25.6)	12,249 (28.1)	3152 (28.9)	3521 (18.1)
Prehospital epinephrine	11,725 (15.9)	6136 (14.1)	1495 (13.7)	4094 (21.1)
On-scene ROSC	6962 (9.4)	4022 (9.2)	985 (9.0)	1955 (10.1)
ED level
Level 1–2	49,440 (66.9)	28,879 (66.3)	7130 (65.4)	13,431 (69.1)
Level 3	24,465 (33.1)	14,697 (33.7)	3764 (34.6)	6004 (30.9)
ECPR	422 (0.6)	238 (0.5)	50 (0.5)	134 (0.7)
Time from call to ECPR pump-on, min	79 (64–97)	78 (62–95)	84 (58–109)	83 (67–97)
Immediate PCI	2042 (2.8)	1155 (2.7)	301 (2.8)	586 (3.0)
Time from call to immediate PCI, min	123 (98–162)	120 (98–158)	121 (97–163)	125 (100–168)
Survived to hospital discharge	7039 (9.5)	4136 (9.5)	1043 (9.6)	1860 (9.6)
Good neurological recovery	3709 (5.0)	2125 (4.9)	543 (5.0)	1041 (5.4)

Categorical variables are presented as numbers (percentages) and continuous variables are presented as medians (interquartile ranges). Immediate PCI is defined as PCI within 6 h from emergency call.

ECPR extracorporeal cardiopulmonary resuscitation, EMS emergency medical services, CPR cardiopulmonary resuscitation, AED automated external defibrillator, RTI response time interval, TTI transport time interval, ROSC return of spontaneous circulation, ED emergency department, PCI percutaneous coronary intervention.

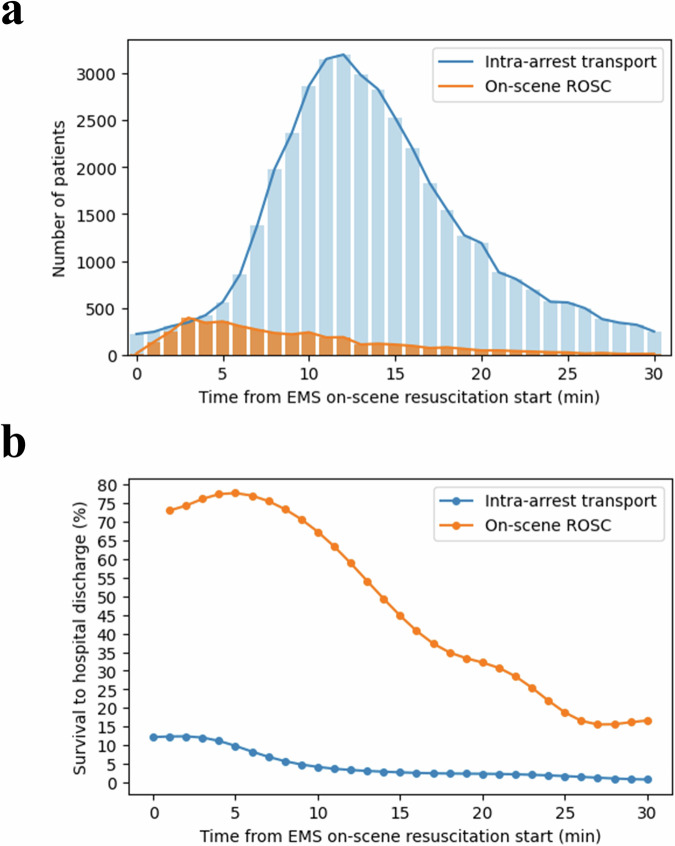
In the training set, the number of patients who were transported intra-arrest peaked at 10–14 min after EMS on-scene resuscitation began. The survival rate for patients transported intra-arrest peaked at 12%, showing a decrease with prolonged on-scene resuscitation times. The survival to hospital discharge rate for patients achieving on-scene ROSC peaked at 78%, subsequently declining with extended on-scene durations (Fig. 3).

Fig. 3. Frequency and survival to hospital discharge rate of patients in the training set who were transported intra-arrest or achieved on-scene ROSC at different on-scene resuscitation times.

a The number of patients who were transported intra-arrest or achieved on-scene ROSC at a specific time point is displayed. b The survival to hospital discharge rate of patients who were transported intra-arrest or achieved on-scene ROSC at a specific time point is displayed. EMS emergency medical services, ROSC return of spontaneous circulation.

The historical on-scene resuscitation times were longer when the OHCA occurred in an urban region or a non-public place, during night hours, when the initial rhythm was non-shockable, and the EMS team level was advanced. Patients who stayed on-scene for less than 15 min received less prehospital advanced airway management (63.9% vs. 85.0%) and prehospital epinephrine (5.9% vs. 27.5%) compared to those who stayed 15 min or more. Among patients in the training set, 238 (0.5%) and 1155 (2.7%) patients received ECPR and immediate percutaneous coronary intervention (PCI), respectively. The time from call to ECPR pump-on was significantly shorter for those with on-scene resuscitation times under 15 min (median [IQR]: 75 [60–94] minutes) compared to those with 15 min or more (median [IQR]: 84 [68–96] minutes). The time from call to immediate PCI was also significantly reduced for patients with on-scene resuscitation times under 15 min (median [IQR]: 118 [95–151] minutes) compared to those with 15 min or more (median [IQR]: 135 [110–176] minutes; Table 2).

Table 2.

Characteristics of patients in the training set according to on-scene resuscitation time

	On-scene resuscitation time		p-value
	<15 min	≥15 min
Total	27,049	16,527
Age, years	73 (59–82)	73 (59–81)	0.35
Sex, male	17,011 (62.9)	10,513 (63.6)	0.13
Diabetes mellitus	5814 (21.5)	3951 (23.9)	<0.001
Hypertension	9140 (33.8)	5784 (35.0)	0.01
Heart disease	4680 (17.3)	2798 (16.9)	0.32
Time of day, daytime (6AM-6PM)	17,353 (64.2)	10,136 (61.3)	<0.001
Region, urban	22,815 (84.3)	14,882 (90.0)	<0.001
ECPR-capable district	12,940 (47.8)	9863 (59.7)	<0.001
Presumed cardiac cause	25,678 (94.9)	15,730 (95.2)	0.25
Place of arrest			<0.001
Public	5203 (19.2)	2127 (12.9)
Non-public	21,840 (80.7)	14,399 (87.1)
Missing	6 (0.0)	1 (0.0)
Witnessed status			<0.001
EMS witnessed	735 (2.7)	182 (1.1)
Bystander witnessed	16,599 (61.4)	9913 (60.0)
Unwitnessed	9524 (35.2)	6368 (38.5)
Missing	191 (0.7)	64 (0.4)
Bystander CPR			<0.001
Dispatcher-assisted	12,048 (44.5)	7458 (45.1)
Unassisted	6267 (23.2)	3028 (18.3)
No CPR	8251 (30.5)	5786 (35.0)
Missing	483 (1.8)	255 (1.5)
Bystander AED use			<0.001
Yes	1518 (5.6)	420 (2.5)
No	25,322 (93.6)	16,019 (96.9)
Missing	209 (0.8)	88 (0.5)
Initial rhythm			<0.001
Shockable	5095 (18.8)	2417 (14.6)
Non-shockable	21,802 (80.6)	14,080 (85.2)
Missing	152 (0.6)	30 (0.2)
EMS team level			<0.001
Advanced	25,426 (94.0)	15,979 (96.7)
Basic	1623 (6.0)	548 (3.3)
Prehospital mechanical CPR	2462 (9.1)	2127 (12.9)	<0.001
RTI, min	7 (5–10)	7 (5–9)	<0.001
On-scene resuscitation time, min	10 (8–12)	18 (16–22)	<0.001
TTI, min	7 (4–11)	6 (4–10)	<0.001
Prehospital airway			<0.001
Endotracheal intubation	1772 (6.6)	1970 (11.9)
Supraglottic airway	15,499 (57.3)	12,086 (73.1)
No	9778 (36.1)	2471 (15.0)
Prehospital epinephrine	1593 (5.9)	4543 (27.5)	<0.001
On-scene ROSC	3340 (12.3)	682 (4.1)	<0.001
ED level			<0.001
Level 1–2	17,613 (65.1)	11,266 (68.2)
Level 3	9436 (34.9)	5261 (31.8)
ECPR	150 (0.6)	88 (0.5)	0.76
Time from call to ECPR pump-on, min	75 (60–94)	84 (68–96)	0.04
Immediate PCI	937 (3.5)	218 (1.3)	<0.001
Time from call to immediate PCI, min	118 (95–151)	135 (110–176)	<0.001
Survived to hospital discharge	3555 (13.1)	581 (3.5)	<0.001
Good neurological recovery	1926 (7.1)	199 (1.2)	<0.001

Categorical variables are presented as numbers (percentages) and continuous variables are presented as medians (interquartile ranges). Immediate PCI is defined as PCI within 6 h from emergency call.

ECPR extracorporeal cardiopulmonary resuscitation, EMS emergency medical services, CPR cardiopulmonary resuscitation, AED automated external defibrillator, RTI response time interval, TTI transport time interval, ROSC return of spontaneous circulation, ED emergency department, PCI percutaneous coronary intervention.

Reinforcement learning model development and evaluation

Figure 1 illustrates the overall flow of the reinforcement learning model development and evaluation process in this study. A patient’s status at each time step (2-min CPR cycle) was modeled as the state, and the decision to continue on-scene resuscitation or initiate transport was considered the action. The on-scene ROSC hazard rate of each individual at each time step was used to derive the intermediate rewards and the actual survival to hospital discharge result of each patient was reflected in the terminal reward. The Random Survival Forest (RSF) model, used to estimate the hazard rate for on-scene ROSC, demonstrated a C-index of 0.882 and an integrated Brier score of 0.067 in the validation set. The average on-scene ROSC hazard rates per time step showed higher rates for patients who actually achieved ROSC compared to those who did not (Supplementary Fig. 1).

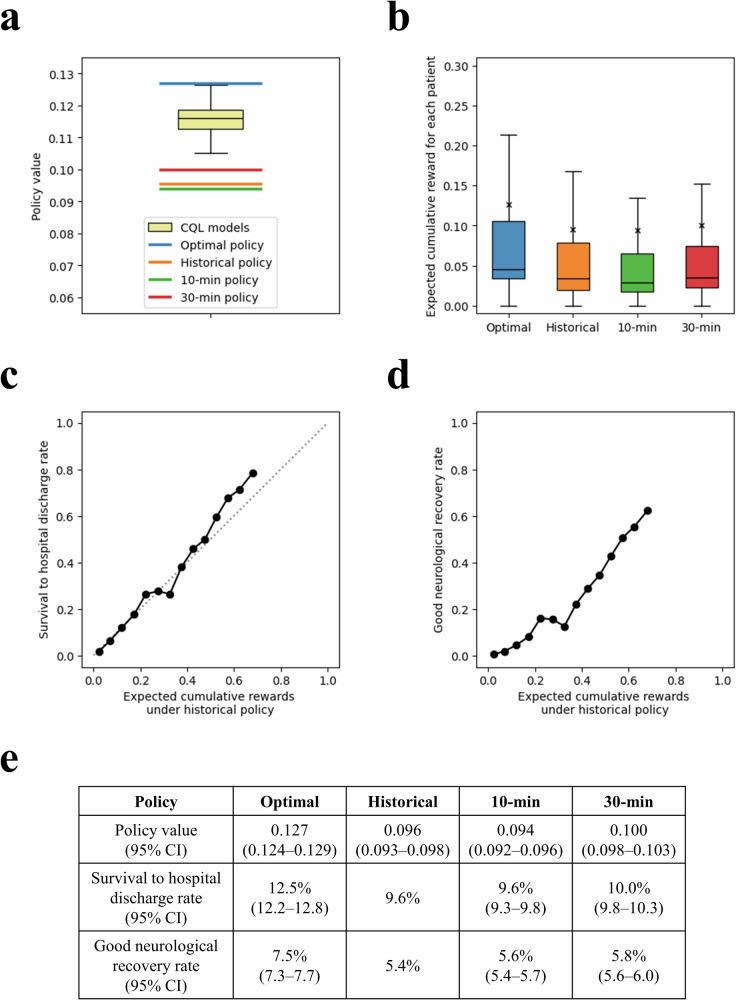
The policy value of the historical policy was 0.096 (95% confidence interval [CI]: 0.093–0.098). The expected cumulative reward for each patient under the historical policy was well-calibrated with the actual survival to hospital discharge rate (Fig. 4). The policy value of the optimal policy, the Conservative Q-Learning (CQL) model with the highest 95% lower bound, was 0.127 (95% CI: 0.124–0.129). For patients whom the optimal policy recommended either a shorter or longer on-scene resuscitation duration, adherence to the policy increased the expected cumulative rewards compared to those in the historical policy (Fig. 5). The optimal policy’s expected survival to hospital discharge rate was 12.5% (95% CI: 12.2–12.8), significantly higher than those of the historical (9.6%), 10-min (9.6%; 95% CI: 9.3–9.8) and 30-min (10.0%; 95% CI: 9.8–10.3) policies. Additionally, its expected rate of good neurological recovery was 7.5% (95% CI: 7.3–7.7), surpassing that of the historical (5.4%), 10-min (5.6%; 95% CI: 5.4–5.7) and 30-min (5.8%; 95% CI: 5.6–6.0) policies (Fig. 4).

Fig. 4. Off-policy evaluation results of different policies in the test set.

a Policy value distribution of 30 CQL models and the optimal, historical, 10-min, and 30-min policies. The policy values of the 30 CQL models are shown as a yellow box plot. The optimal policy is the CQL model that maximized the 95% lower bound of the policy value. The 10-min policy was defined as a policy with 10 min of on-scene resuscitation if ROSC is not achieved on-scene. The 30-min policy was defined as the approach with 30 min of on-scene resuscitation if ROSC is not achieved on-scene. b The distribution of expected cumulative rewards for patients under each policy is shown. The mean expected cumulative rewards under each policy are shown as “x”. Relationship between expected cumulative rewards under historical policy and (c) survival to hospital discharge rate and (d) good neurological recovery rate. e Policy values, expected survival to hospital discharge rate, and expected good neurological recovery rate of each policy. CQL conservative Q-learning, CI confidence interval, ROSC return of spontaneous circulation.

Fig. 5. Changes in expected cumulative rewards according to the difference in on-scene resuscitation time between the optimal and historical policy.

a The difference in expected cumulative rewards becomes greater as the divergence in on-scene resuscitation times increases. b The numbers of patients according to the difference in on-scene resuscitation times are shown.

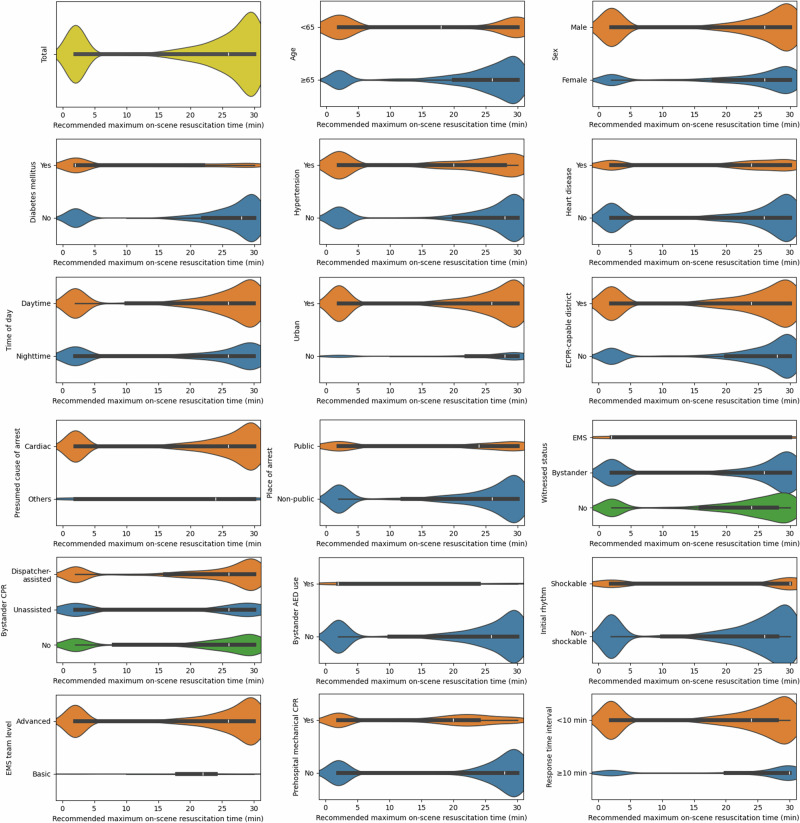
The recommended maximum on-scene resuscitation time exhibited a bimodal distribution, with a median of 26 min and peaks at 2 and 28 min (Fig. 6). The proportion of patients with a recommended maximum on-scene resuscitation time of less than 6 min was greater among those with younger age, male sex, comorbidities, an urban or ECPR-capable location, application of bystander automated external defibrillator (AED), and initial shockable rhythm (Supplementary Table 1). Witnessed by EMS, basic EMS team level, application of mechanical CPR in the prehospital, and shorter response time interval (RTI), were also associated with a shorter median recommended maximum on-scene resuscitation time (Fig. 6).

Fig. 6. Violin plots of recommended maximum on-scene resuscitation times for patients in the test set according to different characteristics.

The recommended maximum on-scene resuscitation time is defined as the recommended duration of on-scene resuscitation in cases where a patient fails to achieve on-scene return of spontaneous circulation. The widths of the violin plots are proportional to the number of patients and are normalized across violins. ECPR extracorporeal cardiopulmonary resuscitation, EMS emergency medical services, CPR cardiopulmonary resuscitation, AED automated external defibrillator.

Ablation study

The optimal policy using only Core Utstein variables increased the expected survival to hospital discharge rate to 11.9% (95% CI: 11.7–12.2) and the good neurological recovery rate to 7.1% (95% CI: 6.9–7.3). The optimal policy including ED level as a variable increased the expected survival to hospital discharge rate to 13.1% (95% CI: 12.8–13.4) and the good neurological recovery rate to 7.9% (95% CI: 7.6–8.1). Overall, the recommended maximum on-scene resuscitation time displayed a similar trend with the main study. When the receiving ED was of higher quality (level 1–2), patients were recommended shorter maximum on-scene resuscitation times (Supplementary Fig. 2).

Implications for settings with termination of resuscitation

We explored the potential implications of the optimal policy for EMS settings where TOR is permitted. When hypothesizing that patients in the training set with Q-values below 0.003 at the time of intra-arrest transport were subject to TOR, the specificity of this TOR rule for predicting death was 0.992 (Supplementary Fig. 3). We then evaluated the performance of a TOR rule based on this criterion in the test set. The sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) were 0.081 (0.077–0.085), 0.984 (0.978–0.989), 0.980 (0.971–0.986), and 0.102 (0.097–0.106), respectively. For the ALS-TOR rule, these values were 0.133 (0.128–0.138), 0.984 (0.978–0.989), 0.988 (0.982–0.991), and 0.107 (0.103–0.112), respectively²⁴.

Discussion

In this nationwide retrospective cohort study, we utilized reinforcement learning to develop models for individualized decision-making in on-scene resuscitation time to optimize the survival outcome for OHCA patients. Data-driven intermediate rewards derived from survival analysis method were incorporated based on domain knowledge to handle the convergence issue of sparse rewards. Our findings indicate that the learned optimal policy is expected to increase the survival to hospital discharge rate from 9.6% to 12.5% and the good neurological recovery rate from 5.4% to 7.5%. The recommended maximum on-scene resuscitation duration varied for different patients, EMS, and OHCA characteristics. During the implementation phase, the recommended maximum on-scene resuscitation time can be determined early using information gathered by the dispatcher or EMS personnel immediately upon arrival at the scene. If a patient achieves on-scene ROSC, transport to the hospital can be initiated; otherwise, the patient can be resuscitated on-scene until the recommended maximum on-scene resuscitation time.

The main contributions of our study are threefold in clinical and methodological aspects. First, to the best of our knowledge, this is the first study to utilize reinforcement learning for individualized decision-making within the context of OHCA research. This approach has the potential to address resuscitation time bias through sequential modeling of changing patient ROSC status. Second, we propose a survival analysis-based and data-driven approach to generating personalized rewards in reinforcement learning, thereby reducing subjectivity in shaping reward values. Third, the reward system we established directly mirrors clinical outcomes, allowing the cumulative reward within our reinforcement learning framework to not merely be proportional to, but also be interpreted as, the probability of survival itself.

Most EMS systems adopt population-based strategies, either the stay-and-play or scoop-and-run policy. While easy to implement, these approaches fail to account for variations in patient characteristics, EMS capability, and circumstances of the OHCA event. This study showed that the 10- and 30-min policies, representing these uniform strategies, were inferior to an individualized optimal on-scene resuscitation time strategy. A previous study employing time-dependent propensity score matching advocated for continued on-scene resuscitation over intra-arrest transport. However, in its subgroup analysis, longer durations of on-scene resuscitation, basic level of EMS, and witness by EMS shifted the preference toward intra-arrest transport⁹. Another study proposed that patients with a higher chance of on-scene ROSC could benefit from a longer on-scene resuscitation time¹³. The evidence from these studies corroborates our hypothesis that an optimal on-scene resuscitation duration exists, varying with specific patient, EMS, and OHCA characteristics.

The recommended maximum on-scene resuscitation time showed a bimodal pattern, with fewer recommendations for durations under 6 min and more recommendations for durations of 24 min or longer. This result aligns with recent evidence suggesting that prolonged on-scene resuscitation benefits the general population, while early intra-arrest transport is advantageous for specific groups that require early in-hospital interventions^9,25. The divergence of our finding from previous studies advocating a shorter on-scene time might be attributed to the lack of consideration for resuscitation time bias in those studies^8,16. One approach to mitigate resuscitation time bias involves employing time-dependent propensity scores to match patients with similar risks of intra-arrest transport⁹. In our research utilizing offline reinforcement learning, we addressed resuscitation time bias through the framework’s dynamic and sequential decision-making capabilities. By incorporating changes in patient state (such as ROSC) and decisions (whether to transport) at each CPR cycle, our approach mitigates resuscitation time bias while allowing individualized decision-making.

In this study, on-scene resuscitation times shorter than 6 min were advocated for patients who were younger, male, diagnosed with heart disease, and with an initial shockable rhythm. Previous research has shown that these characteristics are associated with a cardiac etiology, provision of PCI, and ECPR, suggesting that these patients could benefit more from early hospital transport to receive timely interventions^25,26. This is further supported by the observation that a large proportion of patients who historically received ECPR or immediate PCI were recommended on-scene resuscitation times of less than 6 min (Supplementary Table 1). Since urban and ECPR-capable areas can usually provide more extensive in-hospital treatments, a shorter on-scene resuscitation time may be preferred. In urban locations, the transport time to a hospital is typically shorter, and a short EMS response time may further imply a short transport duration. Given that the period of low-quality compressions delivered in a moving ambulance would be reduced under these circumstances, early intra-arrest transport may be advisable as observed in our study. Furthermore, a basic-level EMS team, limited in performing intubation and administering epinephrine, may benefit from earlier hospital transport to access ALS services.

Interestingly, the majority of patients who may be potential candidates for ECPR, according to previous studies, were recommended short on-scene resuscitation times (Supplementary Fig. 4)^14,25. This result aligns with previous studies that emphasized the importance of shorter time to ECPR for favorable outcomes in patients with OHCA^27,28. It also implies that while only a portion of these patients would have refractory ventricular arrhythmias or be able to receive ECPR due to hospital circumstances, early intra-arrest transport without delay may still be beneficial.

To address the issue of sparse rewards and enhance learning efficiency, we introduced data-driven intermediate rewards based on knowledge of survival analysis. The empirical design of these rewards could lead to subjectivity in determining optimal outcome of mathematically formulated clinical problems because coefficients and values in rewards of reinforcement learning may be arbitrarily determined and optimal outcome can also be affected by values of rewards. Thus, we adopted the hazard function, which can be viewed as a discrete version of the time-derivative of the probability of an event (e.g., on-scene ROSC in our study), to provide a clear, data-driven, and knowledge-based method for reward shaping. This approach enables the model to balance the survival benefits of achieving on-scene ROSC against the potential decrease in survival rate due to delayed transport during intra-arrest. Moreover, considering that the primary evaluation metric of our study is survival probability, using the hazard function as the basis for designing rewards is both logical and intuitive in terms of explainability. When reinforcement learning problems are defined in clinical settings, the values of rewards for establishing value functions and Q-functions are sometimes vague and subjective even though experts’ views are reflected^19,29,30. Our approach was able to relieve this issue by considering that rewards can also be designed by data and knowledge of methods of survival analysis.

Another approach we adopted to improve the learning efficiency of the reinforcement learning model was employing Factor Analysis of Mixed Data (FAMD) to reduce the state space dimensions³¹. FAMD outputs effectively captured the essential information of the original data: the first axis predominantly captured data regarding witness and bystander resuscitation; the second and fourth focused on patient characteristics and initial rhythm; while the third axis concentrated on information pertinent to the EMS (Supplementary Fig. 5). Since patient and EMS characteristics remain constant over time, reducing the dimensions for these features can help the reinforcement learning model concentrate on learning the changes in ROSC status over time.

The expected cumulative rewards for patients were well calibrated with the actual survival to hospital discharge rates (Fig. 4). This suggests that the reward system we designed is effectively structured for a reinforcement learning task aimed at optimizing survival to hospital discharge in patients with OHCA. Moreover, the expected cumulative reward for each patient can be directly considered as the probability of survival to hospital discharge for that specific patient, with a one-to-one ratio. The advantages of this approach include the intuitive interpretability of the expected cumulative reward and the simplified performance evaluation of various policies within this reward framework.

Given that TOR is frequently performed in ALS-based EMS systems, we explored the potential integration of the developed optimal policy with a TOR rule. The specificity of applying TOR for patients who did not achieve on-scene ROSC and had Q-values below 0.003 was 0.984, comparable to the ALS-TOR rule (0.984), though both were slightly below the recommended 0.99 specificity for TOR rules³². The Q-value-based TOR rule can be applied alongside the optimal policy at every 2-min CPR cycle to determine whether to remain on-scene, initiate intra-arrest transport, or terminate resuscitation (Supplementary Fig. 3). While the optimal policy was developed in a setting without TOR, it can be adapted for use with Q-value-based or conventional TOR rules in other systems.

The shift towards personalized medicine marks a significant evolution in healthcare, promising more effective treatments tailored to individual characteristics³³. However, the integration of personalized medicine into OHCA research is limited, with studies mainly focused on predicting individual patient outcomes or analyzing treatment responses by clustering different patient groups³⁴. Reinforcement learning is effective for individualized decision-making, particularly in scenarios where patients’ statuses change over time, necessitating sequential, time-sensitive decisions to optimize outcomes.

This study has several limitations that warrant attention. First, the retrospective design may introduce the potential for unmeasured biases. Second, inaccuracies in recording on-scene resuscitation times cannot be ruled out, as EMS personnel record these times post-event. Third, our approach involved offline reinforcement learning and off-policy evaluation for model development and validation. The data may have some limitations in sufficiently covering the entire state and action space, possibly leading to suboptimal model performance or biases in estimated outcomes. Fourth, our findings may not be universally applicable across different EMS and hospital settings. The advantage of earlier intra-arrest transport may vary depending on the capabilities of the EMS and the receiving hospital. Since advanced emergency medical technicians (EMTs) are only permitted to perform ALS under direct medical oversight in Korea, the frequency of advanced airway management and epinephrine administration is lower than in Western countries. Additionally, ECPR is not yet widely implemented in Korea, and patients in the defined ECPR-capable districts may not have been actually capable of receiving ECPR. Fifth, we did not consider on-scene rearrests after ROSC because we hypothesized that transport to the hospital would have been immediately initiated for most patients who achieved on-scene ROSC, assuming that the incidence of rearrests on-scene would be infrequent. Sixth, due to our exclusion criteria, we were unable to identify patients who might benefit from on-scene resuscitation times exceeding 30 min. Finally, the real-world implementation of the optimal policy might be hindered by practical challenges in adhering to the recommended on-scene resuscitation times under varying circumstances. For example, OHCAs occurring in confined or dark spaces, private houses with many stairs, or involving patients who are too obese to move, can all present significant challenges.

Further research is planned to implement the developed model in the clinical field. We will investigate not only the timing of transport but also the choice of hospital destination, incorporating geospatial information to optimize individualized transport strategies for OHCA patients. Additionally, we plan to conduct a pragmatic clinical trial to investigate the integration of this model into EMS and assess its effectiveness in improving patient outcomes.

In conclusion, this study utilized reinforcement learning to establish individualized optimal on-scene resuscitation times. Our findings suggest that implementing an individualized policy could significantly improve the survival to hospital discharge and good neurological recovery rates in patients with OHCA. In the engineering aspects, we proposed a survival analysis-based, data-driven approach to generate explainable rewards. This approach aims to minimize the subjectivity of optimality and address the issue of sparse rewards in reinforcement learning. We believe that our approach holds potential for intuitively designing reinforcement learning-based formulations with reduced ambiguity in various healthcare problems.

Methods

Study design and setting

This retrospective cohort study utilized data from the nationwide KOHCAR during the period from January 2016 to December 2019³⁵. Data from 2016 to 2018 were randomly divided in an 8:2 ratio into training and validation sets, respectively. The data from 2019 were used as the test set. The study received ethical approval from the institutional review boards of Seoul National University Hospital (IRB No. 1103-153-357), and the requirement for informed consent was waived owing to the study’s retrospective design and the anonymization of patient data.

Korea’s public EMS system is exclusively operated by the National Fire Agency, encompassing 18 provincial fire departments and dispatch centers, covering the entire population of approximately 50 million across 100,210 km². The EMS is a multi-tiered system that offers basic to intermediate levels of care. EMS providers in Korea include nurses and EMTs at both basic and advanced levels. Nurses and advanced EMTs are authorized to provide ALS, including advanced airway management and fluid administration, under direct medical oversight. In contrast, basic EMTs are limited to BLS services, such as CPR and the use of AEDs³⁶. Prehospital mechanical CPR can be initiated before departure from the scene if the device is available in the ambulance³⁷. Prehospital ECPR is currently not implemented and ECPR is only possible in a limited number of hospitals³⁸. Physicians are not dispatched on scene and EMS personnel are not authorized to declare death at the scene unless signs of irreversible death are evident; thus, all patients with OHCA are transported to the nearest ED without TOR. EDs are categorized into three levels: level 1 (38 facilities) and level 2 (119 facilities) handle the highest patient volumes and are staffed with emergency physicians at all times, while level 3 (261 facilities) can be staffed by general physicians³⁹.

Data source

The KOHCAR, initiated in 2008, captures all EMS-treated OHCA patients in Korea. This comprehensive registry merges information from EMS run sheets, the EMS OHCA registry, and hospital medical records. Data recorded by EMS professionals on the EMS run sheets and OHCA registry include patient demographics, OHCA event circumstances, and EMS interventions. Trained medical record reviewers extract details on in-hospital care and clinical outcomes of patients with OHCA. The KOHCAR undergoes monthly quality control checks, with feedback provided to both EMS providers and medical record reviewers to ensure data accuracy and reliability^35,39.

Study population

This study included adult (aged ≥18 years), EMS-treated OHCA patients with a medical cause of arrest. Exclusions were applied to patients with (1) a non-medical etiology such as trauma, asphyxia, drowning, poisoning, or burns; (2) do-not-resuscitate orders; (3) transport initiated prior to cardiac arrest; and (4) lacking information on on-scene resuscitation time or the status or timing of on-scene ROSC. Additionally, cases with an on-scene resuscitation time exceeding 30 min were excluded due to their small number, which could lead to unreliable analysis results. The inclusion criteria were determined based on previous research and aimed to develop an individualized policy for a broad range of patients, encompassing those with shockable and non-shockable rhythms^9,16.

Study outcomes

The primary outcome of this study was survival to hospital discharge. The secondary outcome was good neurological recovery, defined as a cerebral performance category score of 1 (good cerebral performance) or 2 (moderate cerebral disability) at hospital discharge⁴⁰.

Variables and measurements

The exact times, up to the minute, of when the dispatchers received the call, when the EMS arrived at the scene, when the EMS started on-scene resuscitation, when a patient achieved ROSC, and when the ambulance departed from the scene were obtained from the KOHCAR. RTI was defined as the duration from when dispatchers received the call to when the EMS arrived at the scene.

Binary variables included sex, history of diabetes mellitus, hypertension, and heart disease, time of day (daytime [6AM-6PM] vs. nighttime [6PM-6AM]), region (urban vs. rural), ECPR-capable district (yes vs. no), presumed cause of arrest (cardiac vs. others), place of arrest (public vs. non-public), bystander AED use (yes vs. no), initial rhythm (shockable vs. non-shockable), EMS team level (advanced vs. basic), prehospital mechanical CPR (yes vs. no), and ED level (levels 1–2 vs. level 3). Witnessed status was categorized into EMS witnessed, bystander witnessed, and not witnessed. Bystander CPR was classified as dispatcher-assisted, unassisted, and no bystander CPR.

The region was classified based on Korea’s administrative districts, which comprises 250 administrative districts designated as cities (Si), counties (Gun), or districts (Gu)⁴¹. Counties (Gun), typically with populations under 100,000, were considered rural areas, while cities (Si) and districts (Gu) were considered urban areas. ECPR-capable district was defined as a district with at least one ECPR case in the training set³⁸. The presumed cause of arrest was considered cardiac if there were no other evident causes, including traumatic, respiratory, bleeding, anaphylaxis, or terminal cancer. A public place included public or commercial buildings, streets or highways, industrial areas, transport terminals, and recreational areas. The EMS team level was categorized as advanced if there was at least one nurse or an advanced EMT present in the team; otherwise, it was considered basic. Immediate PCI was defined as PCI which was performed within 6 h from emergency call⁴².

Continuous variables, including age and RTI, were normalized to have a zero mean and unit variance in the training set. Categorical variables with multiple categories were one-hot encoded.

Markov decision process design

Determining the optimal duration of on-scene resuscitation for each patient can be regarded as a sequential decision-making process of deciding whether to continue resuscitation on the scene or to initiate patient transport at each time step. The unit time steps were two-minute intervals reflecting the fact that the duration of one CPR cycle is two minutes. The initial time step (t = 0) corresponds to the moment when EMS arrives at the scene, while the final time step is when a patient is transported intra-arrest or has achieved on-scene ROSC.

This decision-making process can be formulated as a Markov decision process^43,44. With the state $s_t\in R^m$, action $a_t\in [0,1]$ (0: on-scene resuscitation, 1: transport), discount factor γ, and trajectory length T, the policy ${\pi }_{\theta }\left(a_t\mid s_t\right)$ should be determined to maximize the expectation values of value function $V_{\pi }$ in reinforcement learning. In addition, the Q-function ${\mathrm{Q}}_{\pi }$ with actions and states can be calculated by the expectation values under the policy. Thus, the goal is to find an optimal policy ${\mathrm{\pi }}^{*}\left({\mathrm{a}}_{\mathrm{t}}\mid s_t\right)$ to maximize V and Q-functions and to investigate the optimal decisions based on the optimal policy.

$${\mathrm{V}}_{\pi }\left(s_t\right)={\mathbb{E}}_{\pi }\left(\sum _{k=t}^T{\gamma }^{k-t}{r}_k\mid s_t\right)$$ 1

$${\mathrm{Q}}_{\pi }\left(s_t,a_t\right)={\mathbb{E}}_{\pi }\left(\sum _{k=t}^T{\gamma }^{k-t}{r}_k\mid s_t,a_t\right)$$ 2

The state construction was achieved through the following methods. Initially, features that could be acquired during the prehospital on-scene phase were identified. These features encompassed age, sex, history of diabetes mellitus, hypertension, heart disease, time of day, region, ECPR-capable district, presumed cause of arrest, place of arrest, EMS witnessed, bystander witnessed, dispatcher-assisted CPR, unassisted CPR, bystander AED use, initial rhythm, EMS team level, prehospital mechanical CPR, and RTI. FAMD was employed to reduce the dimensions from 19 to 11, explaining 82% of the variance³¹. The final state space spanned 13 dimensions, integrating the 11-dimensional output from the FAMD, ROSC status, and normalized time step. Normalization of the time step involved subtracting the mean on-scene resuscitation time from the training set then dividing the difference by the standard deviation of the on-scene resuscitation time in the training set.

The possible actions consisted of on-scene resuscitation (action = 0) or transport (action = 1). For instance, for a patient transported after 10 cycles (20 min) of on-scene resuscitation without achieving ROSC, the actions from t = 0 (EMS arrival at scene) to t = 9 would be 0, indicating on-scene resuscitation, and the action at t = 10 would switch to 1, indicating the decision to transport. The successive sequences of states and actions for a patient were termed a patient’s trajectory. A change from one state to the next as a result of taking an action is referred as a transition.

Data-driven rewards from survival analysis

In our study, designing the proper reward function is important to achieve unbiased results and clinical interpretability. Initially, we designed the reward system to assign a positive reward of +1 at the end of the trajectory for patients who survived to hospital discharge, while no reward was given to patients who did not survive. However, the CQL model failed to identify an optimal strategy due to the sparsity of rewards; the rewards for training the Q-function only existed for the terminal transitions (action = 1)⁴⁵. To overcome this challenge, we introduced intermediate rewards based on the hazard rate from a survival analysis of on-scene ROSC for intermediate transitions (where action = 0). The underlying rationale was that on-scene resuscitation efforts could be rewarded based on the expected survival benefit associated with achieving on-scene ROSC at the time step. We first fitted a RSF model in the training set with on-scene ROSC as the event, treating intra-arrest transport as censored data⁴⁶. Hyperparameters were determined through grid search using the validation set for evaluation. Subsequently, we determined the hazard rate function for each individual at time step t using the RSF model, which refers to the proportion of patients who will achieve on-scene ROSC, per unit time, relative to those who remain at the scene without ROSC at a given timestamp t. In addition, to link on-scene ROSC and final survival outcomes, the average survival to hospital discharge rate for patients who experience on-scene ROSC at a certain time t was also introduced. Thus, the intermediate reward ${\mathrm{r}}_{\mathrm{t}}$ for a transition was defined as the product of the hazard rate ($h_t$) and the average survival to hospital discharge rate $S\left(t\right)$ of patients who achieved ROSC at the corresponding time step t. Terminal rewards ($r_T)$ were given at the terminal transitions so that the cumulative rewards would be 1 for a patient who survived to hospital discharge (${\delta }_T=1)$ and 0 for a patient who did not survive (${\delta }_T=0)$, where ${\delta }_T$ is an indicator variable for final survival of a patient.

The discount factor (γ) was set to 1, indicating that future rewards are considered equally important as intermediate rewards. With the trajectory length $T$, state at time t ($s_t$), hazard rate ($h_t$) of on-scene ROSC, average survival rate in case of on-scene ROSC at time t ($S\left(t\right))$, and terminal reward ($r_T)$, the cumulative reward $R_T\left({\delta }_T\right)$ is represented as below.

$${\mathrm{r}}_{\mathrm{t}}=\left\{\begin{array}{c}\hfill h_t\left(s_t\right)S\left(t\right)if0\le t\le T-1\left(\mathrm{intermediate}\mathrm{reward}\right)\hfill \\ \hfill R_T\left({\delta }_T\right)-\sum _{\left(t=0\right)}^{\left(T-1\right)}{h}_t\left(s_t\right)S\left(t\right)ift=T\left(\mathrm{terminal}\mathrm{reward}\right)\hfill \end{array}\right)$$ 3

$$R_T\left({\delta }_T\right)=\sum _{t=0}^{T-1}{h}_t(s_t\left)S\right(t)+r_T=\left\{\begin{array}{c}1,\mathit{if\; the\; patient\; survives\; to\; hospital\; discharge}\\ 0,\mathit{otherwise}\end{array}\right)$$ 4

Reinforcement learning model development

Offline reinforcement learning optimizes decision-making using pre-collected data without further environment interaction. It offers a valuable approach for the medical field where interactions with patients during training may pose risks⁴⁴. We employed CQL, a reinforcement learning algorithm designed to learn a conservative Q-function⁴⁷. The Q-function quantifies the expected future rewards for taking a given action in a specific state, guiding the selection of optimal actions by estimating the total reward attainable from that point onwards. CQL ensures that the expected value of a policy under the Q-function is a lower bound to its true value, thereby minimizing the overestimation of out-of-distribution actions. CQL has demonstrated good performance in offline reinforcement learning problems, including tasks within the medical domain¹⁹. The CQL model utilized the Double Deep Q Network framework with two hidden layers of 128 units each⁴⁸. A replay buffer containing all transitions from the training set was constructed, and the model was trained using transitions randomly sampled from the buffer until the validation set loss stabilized. Adam optimizer was used, the learning rate was set to 0.0001, the conservatism parameter (α) to 0.001⁴⁹, and batch size was 32. Thirty models were built using different random seeds, and the model that maximized the 95% lower bound of the policy value was chosen as the optimal policy (Table 3)¹⁹.

Table 3.

The algorithmic process of our approach

Input: OHCA data
Output: Weights of neural networks for optimal policy ${\mathrm{\pi }}^{*}$ and Q-functions
#1. Train a hazard function model for the event of on-scene ROSC based on RSF → $h_t$ #2. Calculate the average survival to hospital discharge rate of patients who achieved ROSC at time step t → $S\left(t\right)$ #3. Compute intermediate rewards ${\mathrm{r}}_t$ and terminal rewards $r_{\mathrm{T}}$ by Eqs. (3) and (4) #4. Construct states ${\mathrm{s}}_{\mathrm{t}}$ through FAMD for dimension reduction process #5. Construct tuples of transitions (${\mathrm{s}}_{\mathrm{t}},a_t,r_t,s_{t+1},{\delta }_t)$ from patient trajectories #6. Train reinforcement learning models: compute weights of double deep Q-network based on CQL using tuples of transitions #7. Derive and evaluate optimal policy from constructed Q functions

OHCA out-of-hospital cardiac arrest, ROSC return of spontaneous circulation, RSF Random Survival Forest, FAMD Factor Analysis of Mixed Data, CQL Conservative Q-Learning.

Off-policy evaluation

Off-policy evaluation assesses a learned policy using historical data⁵⁰. We employed fitted Q-evaluation (FQE), a model-free approach that utilizes function approximation, with bootstrapping to acquire the CIs⁵¹. This technique enables a more accurate estimation of a given policy’s Q-function compared to the Q-function learned during training⁵². FQE was applied to the test set to estimate the policy value, defined as the average of cumulative rewards for each patient.

We compared four distinct policies: optimal, historical, 10-min, and 30-min policies. The historical policy precisely follows the on-scene resuscitation times recorded in the dataset. In the 10-min policy, the EMS conducts on-scene resuscitation for 10 min before initiating transport if on-scene ROSC is not achieved. In the 30-min policy, the EMS undertakes on-scene resuscitation for 30 min prior to transport initiation if on-scene ROSC is not achieved. Transport was initiated when on-scene ROSC was achieved or after 30 min of on-scene resuscitation in all policies.

To estimate the expected outcomes of each policy, we correlated the expected cumulative rewards for each patient under the historical policy with the outcomes. We categorized the cumulative rewards into 0.05-width bins, calculating the average survival to hospital discharge and good neurological recovery rates for each policy. Applying this binning approach, we estimated the expected outcomes of the optimal, 10-min, and 30-min policies.

Determining the recommended maximum on-scene resuscitation time

The recommended maximum on-scene resuscitation time is defined as the recommended duration of on-scene resuscitation in cases where a patient fails to achieve on-scene ROSC. If a patient achieves ROSC before this time, the patient would be immediately transported to the hospital. This duration can be identified by comparing the Q-values for intra-arrest transport (action = 1) and on-scene resuscitation (action = 0) at each time step, from 0 to 30 min, assuming the patient has not achieved on-scene ROSC. The recommended maximum on-scene resuscitation time is determined as the time point when the Q-value for action = 1 surpasses that for action = 0 (Supplementary Fig. 3). Since it is based on the assumption that on-scene ROSC has not been achieved, the recommended maximum on-scene resuscitation time can be determined early on using the patient’s initial characteristics rather than requiring real-time updates on the patient’s ROSC status at each step.

Ablation study

Two ablation studies were conducted to observe the performance of the models in settings where the obtainable variables differ. First, we utilized only Core Utstein variables (i.e., core data elements used internationally for reporting OHCA patients: age, sex, presumed cause of arrest, place of arrest, EMS witnessed, bystander witnessed, dispatcher-assisted CPR, unassisted CPR, bystander AED use, initial rhythm, EMS team level, and RTI)⁵³. Second, ED level was added as a state in the main model, assuming that the transport destination would not be changed from the historical ED. FAMD was employed to ensure that the final dimension of the state space matched that of the main study. The rest of the methods remained consistent with the original analysis.

Implications for settings with termination of resuscitation

We analyzed the Q-values of the optimal policy at the historical time of intra-arrest transport. Since Q-values are calibrated with survival rates, a low Q-value indicates a low probability of survival at that moment. Based on the finding that the specificity of performing TOR for patients with Q-values below 0.003 at the time of intra-arrest transport was 0.992, we established a Q-value-based TOR rule using this threshold. These criteria were applied to test set patients at the historical transport time, and the sensitivity, specificity, PPV, and NPV of TOR to predict death were analyzed. For comparison, the ALS-TOR rule was also applied at the historical transport time, and its test characteristics were analyzed. The ALS-TOR rule is known for its high specificity in predicting death and recommends TOR when all five criteria are met: (1) no shock delivered, (2) the arrest was not witnessed by a bystander or (3) EMS personnel, (4) no bystander CPR was provided, and (5) no ROSC was achieved before transport²⁴.

Statistical analysis

Categorical variables were presented as numbers and proportions, with the chi-square test utilized for group comparisons. Continuous variables were presented as medians and IQRs, and comparisons between groups were conducted using the Mann–Whitney U test or Kruskal–Wallis test, as appropriate. A two-sided p-value of less than 0.05 was deemed statistically significant. While there were missing data for place of arrest, witnessed status, bystander CPR, bystander AED use, and initial rhythm, the proportions of missing data were less than 3% for all variables. Missing data were imputed using stochastic regression imputation with logistic regression^39,54. Cases with missing on-scene resuscitation time or the status/timing of on-scene ROSC were excluded rather than imputed. This exclusion is based on the following rationale: (1) these variables determine the length of a patient’s trajectory, which is critical in reinforcement learning; (2) missing values make it impossible to ascertain if ROSC was achieved on-scene; and (3) these variables are used as outcomes in the Random Survival Forest model⁵⁵. The discrimination and calibration performance of the fitted RSF model was evaluated using the C-index and integrated Brier score in the validation set¹³.

All statistical analyses were conducted using Python version 3.8.12 (Python Software Foundation, Wilmington, DE, USA) and SAS version 9.4 (SAS Institute Inc, Cary, NC, USA). The development and evaluation of reinforcement learning models were performed using d3rlpy library version 2.3.0⁵⁶.

Author contributions

D.H.C.: conceptualization, methodology, software, formal analysis, investigation, writing–original draft, and funding acquisition. M.H.L.: methodology, software, validation, formal analysis, investigation, writing–original draft, and funding acquisition. K.J.H.: conceptualization, validation, data curation, writing–review & editing, and supervision. Y.G.K.: visualization and writing–original draft. J.H.P.: conceptualization and data curation. K.J.S.: conceptualization and data curation. S.D.S.: conceptualization and supervision. S.K.: conceptualization, validation, and supervision. All authors have read and approved the manuscript.

Data availability

The data analyzed during the current study are not publicly available due to institutional restrictions on data privacy but may be available from the corresponding author on reasonable request.

Code availability

The codes that were used to develop and evaluate the reinforcement learning models in this study can be accessed at https://github.com/dhcsnu/on-scene-time-ohca.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41746-024-01278-3.