Near-critical Stranski-Krastanov growth of InAs/InP quantum dots

Abstract

This work shows how to control the surface density and size of InAs/InP quantum dots over a wide range by tailoring the conditions of Stranski-Krastanov growth. We demonstrate that in the near-critical growth regime, the density of quantum dots can be tuned between ${10}^7$ and ${10}^{10}$ ${\text{cm}}^{-2}$. Furthermore, employing both experimental and modeling approaches, we show that the size (and therefore the emission wavelength) of InAs nanoislands on InP can be controlled independently from their surface density. Finally, we demonstrate that our growth method gives low-density ensembles with well-isolated QD-originated emission lines in the telecom C-band.

Introduction

Rapidly developing applications of III-V semiconductor quantum dots (QDs) as nonclassical quantum light sources impose stringent conditions on their properties. Meeting these requirements presents new challenges in QD synthesis^1–4. The stress-driven, so-called Stranski-Krastanov (SK)⁵, method to grow semiconductor QDs is widely used for a broad range of device applications^6–9. This method has been studied theoretically and experimentally for several semiconductor materials, including InAs/GaAs, InAs/InP, Si/Ge and others^7–9. However, emerging device applications, such as single QD-based nonclassical photon emitters or entangled-photon pairs sources, present new demands in terms of density and morphology of QD ensembles, which are not always compatible with the previous approaches^3,6,10–12 and require substantial modifications to the growth conditions. In particular, quantum devices accessing individual QDs require highly tailored growth of low surface density QD ensembles, which has so far remained challenging using the SK method.

Theoretical models describe the SK formation of QDs as the phase transition between the strained 2D wetting layer (WL) and the partially relaxed 3D nanostructures^13–19. According to the generally accepted theory, formation of the 3D islands becomes thermodynamically preferable to the 2D WL growth when the nominal thickness of the deposited layer (denoted as h) exceeds the equilibrium value (denoted as $h_{\mathit{eq}}$). The difference between h and $h_{\mathit{eq}}$ characterizes the supersaturation (or superstress) of the WL, which determines the extra energy avaliable for QD formation, and thus, the rate of QD nucleation^18–20. Based on this model, the pace of transition from the WL to the QDs increases with the WL thickness (and strain accumulation) until the WL consumption rate is large enough to balance the material influx from the precursors of the growth species. This corresponds to the so-called “critical” thickness of the WL denoted as $h_c$ which limits the real achievable thickness of the WL during the QD nucleation. We note that the term “critical” here should not be confused with the critical layer thickness for the formation of dislocations.

In the case of a highly superstressed system, when h reaches the critical value $h_c$, the phase transition has a “supercritical” character. This implies the fast nucleation of a high number density of QDs (typically ${10}^{10}-{10}^{11}$ ${\text{cm}}^{-2}$), leading to a rapid decline in superstress and preventing further QDs nucleation^19,20. In contrast, when the thickness of the WL is below the critical value but exceeds the equilibrium value ($h_{\mathit{eq}}<h<h_c$), the phase transition has a subcritical character. In this case, nucleation of subcritical QDs occurs at lower supersaturation compared to the supercritical case and is thus much slower. As a result, the surface density of subcritical QDs is one or two orders of magnitude lower than in the supercritical case. However, continuous nucleation leads to a large difference in growth duration from QD to QD, and thus, results in a large dispersion in the size of the QD ensemble¹⁹.

Subcritical and supercritical nucleation have previously been studied theoretically and explored experimentally, mainly for the In(Ga,As)/GaAs material system^21–23. However, the intermediate nucleation at $h\approx h_c$, which we refer to as “near-critical”, remains less scrutinized. The systematic investigation of this regime for InAs QDs formation on GaAs substrates is difficult due to a rather small critical thickness $h_c\approx$ 1.7 ML, which is close to $h_{\mathit{eq}}$²¹. In contrast, InAs/InP system has a larger difference between $h_c$ of around 4 ML and $h_{\mathit{eq}}$ of around 3 MLs according to recent experimental observations²⁴. Besides, achieving the emission in the telecom C-band in the InAs/GaAs system requires a few-hundred-nm InGaAs metamorphic buffer layer between GaAs substrate and the InAs QDs^25–27. While the QDs with emission in C-band with the surface density around ${10}^8{\text{cm}}^{-2}$ is reported previously in the sub-critical growth²⁸. Meanwhile, InAs/InP SK growth does not require an intermediate layer. Furthermore, in contrast to the In(Ga,As) case, the thickness of the In(As,P) layer on top of InP can be tuned not only by the layer deposition but also by employing the interchange of P and As atoms at the interface during the annealing under the flux of arsenic precursor.

In this work, we demonstrate how to obtain a high degree of control over the surface density and the size of SK InAs/InP QDs over a wide range by tailoring the growth parameters. InAs QDs on InP(100) surface densities of ${10}^{10}-{10}^{11}$ ${\text{cm}}^{-2}$ are readily accessible within the supercritical growth, while in the near-critical regime, we show how the low density of QDs can be tuned within a very wide range between ${10}^7$ and ${10}^{10}$ ${\text{cm}}^{-2}$. In addition, we explain how the size of InAs nanoislands on InP can be controlled independently from the surface density. Moreover, we measure the photoluminescence response from the low-density QDs ensemble, revealing sharp and well-isolated emission lines within the C-band originating from the recombination of excitonic complexes confined to individual QDs.

Results and discussion

In the InAs/InP material system, there are two mechanisms to form epitaxial 2D In(As,P) layers. The first mechanism is the conventional epitaxial growth with both group III and V precursors supplied. The second one is a self-limited process of substitution of P atoms to As atoms during the annealing of InP in ${\text{AsH}}_3$ ambient^29,30. The V^th group atoms exchange is driven by the P desorption from the III-V surface at temperatures above ${350}^{\circ }\text{C}$²⁹. Here we employ both mechanisms and mainly discuss the growth by metal-organic vapor phase epitaxy (MOVPE). The details of the MOVPE process are given in the Methods section. However, similar considerations would also be applicable in the case of molecular beam epitaxy (MBE)²⁹.

Growth modes of InAs on InP under As flux

Under the standard growth conditions, when the InP surface is exposed to ${\text{PH}}_3$ ambient, the desorbing P atoms leave behind vacant adsorption sites, which are immediately filled with the phosphorus from the gas phase. In the case of annealing of the InP surface in the ${\text{AsH}}_3$ ambiance, the As atoms bind to available indium atoms left vacant due to P desorption²⁹. The kinetics of As substitution of P atoms is temperature-dependent and the process is self-limited and reversible, as experimentally observed in Ref. ²⁹.

As mentioned earlier, from the model point of view, the transition between 2D and 3D growth becomes energetically favorable with the thickening of the WL. Figure 1a–c show the scanning transmission electron microscopy (STEM) images of the WLs formed in the three cases of InP substrate annealed at ${485}^{\circ }\text{C}$ under ${\text{AsH}}_3$ flow of $5.5·{10}^{-5}\mathrm{mol}/\min$ for 4, 30 and 600 s, respectively. We have measured the thicknesses of the obtained In(As,P) layers based on the contrast in the STEM images and estimated the chemical composition of the layers from analyzing the spacing of the crystal lattice planes along the [001] growth direction. The analysis uses the Poisson’s ratio of the crystal to estimate composition based on the observed deformation due to strain³¹. It is crucial to note here that STEM analysis generally is not capable of large-area studies and the presented images show only small areas compared to the sizes of the samples. Therefore, besides STEM imaging, we use atomic force microscopy (AFM) to analyze the density and morphology of QDs. The details of STEM and AFM measurements are given in Methods section.

Fig. 1.

Cross-section HAADF STEM images of InAs layers formed after InP annealing in the ${\text{AsH}}_3$ ambient at ${485}^{\circ }\text{C}$ and ${\text{AsH}}_3$ flow of $5.5·{10}^{-5}\mathrm{mol}/\min$ during: (a) $4\text{s}$, (b) $30\text{s}$, (c) $600\text{s}$; and after $30\text{s}$ of annealing followed by additional deposition of (d) 1.14 ML and (e) 1.65 ML of InAs at V/III ratio of 5 and growth rate of 0.49 ML/s.

Figure 1a shows the STEM image of an approximately 2 ML-thick ${\text{InAs}}_{0.18}$ ${\text{P}}_{0.82}$ layer formed after annealing for $4\text{s}$ and subsequently covered by InP. Longer annealing promotes the formation of a thicker In(As,P) layer with higher As concentration. Fig. 1b,c show approx. 4 ML-thick layers of ${\text{InAs}}_{0.7}$ ${\text{P}}_{0.3}$ and ${\text{InAs}}_{0.75}$ ${\text{P}}_{0.25}$ formed after $30\text{s}$ and $600\text{s}$ of annealing in ${\text{AsH}}_3$, respectively. The In(As,P) layer thickness and As concentration after annealing for $600\text{s}$ is close to saturation under the given conditions. No indication of plastic relaxation in the structures and QD formation could be found in the STEM images (Fig. 1a–c). Therefore, the thickness and composition of the In(As,P) layer can be tuned by varying the duration of InP annealing under the ${\text{AsH}}_3$ flux. Meantime, under the considered experimental conditions, the thickness of the formed InAs(P) WL is not sufficient to initiate the formation of 3D islands.

To approach the limit of 2D growth, the thickness and concentration of As in the In(As,P) layer need to be increased by further deposition of InAs. When the InAs layer exceeds the equilibrium thickness $h_{\mathit{eq}}$, the release of the accumulated elastic strain in the system leads to material redistribution, resulting in modulated thickness of the layer. These thickness modulations can be observed in the STEM image shown in Fig. 1d. Namely, the deposition of  $\sim$1.1 ML of InAs on top of the In(As,P) layer (formed after annealing in ${\text{AsH}}_3$ for 30 s, similar to Fig. 1b), results in 1-2 ML thickness modulations on top of the $\sim$4 ML-thick In(As,P) with $\sim 95\%$ of As (Fig. 1d). As we discuss later in the AFM analysis, this thickness of InAs layer is enough to form very diluted arrays of QDs with surface densities below or far below ${10}^8{\text{cm}}^{-2}$.

Further increase of the InAs layer thickness beyond the critical value $h_c$ leads to the formation of an array of coherently strained islands with their surface density exceeding ${10}^{10}{\text{cm}}^{-2}$. Figure 1e is an image of the self-assembled QDs after the deposition of 1.65 MLs of InAs in addition to $30\text{s}$ annealing under ${\text{AsH}}_3$. Ensembles of similar number density QDs can serve as the effective gain medium for lasing structures with a photonic crystal cavity^32,33. However, the fabrication of nonclassical photon sources based on a single QD requires much lower surface densities leading to a substantial QD-to-QD separation^10,34. The partially consumed WL between the QDs in Fig. 1e is about 2 ML thinner than the one after As-P exchange (Fig. 1b). The WL composition in this sample is estimated to be ${\text{InAs}}_{0.9}$ ${\text{P}}_{0.1}$ and the QD composition is close to pure InAs.

In summary, As-P exchange during the InP annealing under ${\text{AsH}}_3$ allows tuning the In(As,P) layer thickness and composition, although it is insufficient for InAs/InP QD formation under the considered growth conditions. Further deposition of InAs leads to QD formation. Deposition of less than 1.1 ML of InAs on top of $\sim$4 ML-thick ${\text{InAs}}_{0.7}$ ${\text{P}}_{0.3}$ is required to exceed the equilibrium thickness, while the critical thickness in the considered structure is observed to be between 1.1 and 1.65 MLs deposited on top of In(As,P) layer.

Importantly, the formation of InAs/InP QDs strongly depends on growth parameters, which we discuss in detail in the following section. As noted above, STEM studies show only very limited areas of the samples, and thus, our STEM results do not indicate the complete absence of QDs after additional deposition of 1.1 ML of InAs. It may just suggest that the QD density is much lower than that after adding 1.65 ML of InAs. These low-density QDs form at the WL thicknesses close to the critical value $h_c$. We further explore this property by depositing of additional 1.1 ML (or less) InAs to obtain low-density near-critical QDs and tune their parameters.

Influence of growth parameters on the properties of QDs

Theoretical approaches^18–20 imply that the rate of QD nucleation is controlled by the superstress, which increases with the amount of deposited InAs. In the supercritical process (at $h$ above $h_c$), large superstress leads to fast nucleation of QDs, which causes material transfer from the WL to QDs thickness (and thus reduction of the superstress). This, in turn, limits the duration of the nucleation phase to a short time interval. In contrast, subcritical nucleation of QDs occurs at low superstress and continues throughout the growth.

In this section, we investigate the formation of near-critical QDs (at $h\sim h_c$) and discuss ways to independently tune their size and surface density.

In the approximation of a short nucleation stage at WL thicknesses near the critical value, the surface density of nanoislands N can be modeled as an abruptly changing (step-like) function $\vartheta$ of the nominal thickness of the deposited InAs layer h^16,19,20:

$$\begin{array}{c}\hfill N(h)=N_0\vartheta (h)\end{array}$$ 1

where $N_0$ is the saturated QD density for $h>>h_c$, which is dependent on the growth kinetics governed by the growth conditions. Following the approach of Ref. ¹⁹ we use the double-exponential expression for $\vartheta (h)=1-exp(-exp[\mathrm{\Gamma }(h-h_c)/(h_c-h_{\mathit{eq}})])$, where $\mathrm{\Gamma }$ is twice the maximum energy required for QD formation. Meantime, as we explain in more detail in Section S1 of the Supplementary Information, $N_0$ can be expressed as the function of the flux rate of the group III precursor $F_{\mathit{In}}$ and the rate of QD growth after nucleation $\nu$¹⁹. For various InAs (001) surface reconstructions, the flux ratio is known to impact heavily the surface reconstruction and In adatom kinetics^35,36. In the case of the group III rich surface (low V/III ratio) the growth of QDs is limited by the transport of group V atoms from the gas phase and thus is assumed to be proportional to the As precursor flux. Meanwhile, at high V/III ratios, one can expect the QD formation on group V saturated surface with the growth rate limited by the surface diffusion of In adatoms. Several studies reported enhancement of In and Ga migration on the surfaces with excess of As^37–39. In closer consideration, the diffusion of group III atoms on top of the WL is impacted by numerous surface processes and still needs to be fully understood. Therefore, to reflect the effect of In migration enhancement in our modeling, we assume that the rate of QD growth $\nu$ linearly increases with the As precursor flux. The simplified model approximation here is linear $\nu (F_{\mathit{As}})$ dependence applicable for the In-limited regime of QD growth. Within this approach, explained in more detail in Section S1 of the Supplementary Information, the QD surface density N can be modeled as the function of the thickness h and V/III ratio $\frac{F_{\mathit{As}}}{F_{\mathit{In}}}$:

$$\begin{array}{c}\hfill N\left(h,,,\frac{F_{\mathit{As}}}{F_{\mathit{In}}}\right)=n{\left(\frac{F_{\mathit{As}}}{F_{\mathit{In}}}\right)}^{\alpha }\vartheta (h),\end{array}$$ 2

with the coefficient n specific for each growth mode. The exponent $\alpha$ depends on the mechanism for the transport of the growth-limiting species.

Thus, we believe that enhancement of In migration is crucial for obtaining low-density ensembles of subcritical QDs in our approach. Previously Enzmann et al. also explained the MBE growth of low-density InAs QDs on AlGaInAs layer lattice matched to InP(001) by enhanced adatom migration⁴⁰. This work used ultra-low growth rates to increase migration length and thus obtain low QD density. Instead, as we show in the next section, in our MOVPE-based approach we use large V/III ratios (usually inaccessible in MBE) to obtain low-density QD ensembles. Next, we discuss the impact of the precursor flux ratio on the QD formation in further detail.

V/III flux ratio

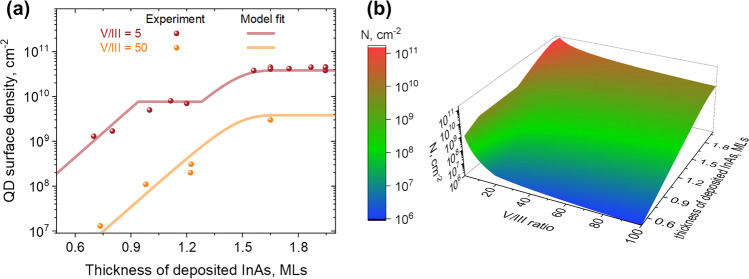
We observe that QD surface density has a different character of dependence on the flux ratio in dense and sparse ensembles of QDs, obtained after deposition of 1.65 and 0.8 MLs of InAs on top of the In(As,P) layer, correspondingly. Figure 2a shows more than two orders of magnitude change of the QD surface density (${10}^7-{10}^9{\text{cm}}^{-2}$) in sparse arrays of QDs while varying the As precursor flux to change the V/III ratio between 2 and 100 as illustrated in Fig. 2a.

Fig. 2.

(a) Variation of QD surface density with V/III ratio in supercritical (red) and near-critical (orange) nucleation. (b,c) Schematics for In and As collection areas in sparse and dense QD ensembles.

As mentioned earlier, the exponent $\alpha$ is determined by the transport mechanism of the limiting growth species. Under As-rich conditions the growth is limited by the transport of In to a QD, and in the excess of In - by the As species. In the case of In-limited (As-rich) growth $\alpha =1$, which corresponds to the surface diffusion of In atoms to the 3D nanoisland from a collection area much larger than the size of an island. This regime corresponds to the experimentally observed dependence at V/III ratios above 20 shown in Fig. 2a. In the case of the As-limited regime the measured dependence for low-density QDs corresponds to $\alpha =3$, which is consistent with the model regime of condensation from a 3D vapor in the ballistic regime¹⁹.

To delineate the In-limited and As-limited regimes, the transport of each growth species to a specific QD can be evaluated by multiplying the precursor flux density $F_i$ (with the index $i=In$ or As) by the area of the collection region around the QD, $A_i$. Here $A_i=\pi {\mathrm{\Lambda }}_i^2$ with ${\mathrm{\Lambda }}_i$ denoting the collection range for the corresponding type of the growth species. Thus, the equation $F_{\mathit{In}}{\mathrm{\Lambda }}_{\mathit{In}}^2=F_{\mathit{As}}{\mathrm{\Lambda }}_{\mathit{As}}^2$ formally defines the boundary between In-rich and As-rich conditions.

The collection range of In is limited either by the surface diffusion length ${\lambda }_i$ or by the mean distance between QDs $l$, depending on which quantity is smaller. Thus, in terms of the notations we introduced above, ${\mathrm{\Lambda }}_i={\lambda }_i$ in sparse ensembles and ${\mathrm{\Lambda }}_i=l\sim 1/\sqrt{N}$ in dense arrays of QDs. Then, depending on the flux rates and QD surface density the following growth regimes can be distinguished:

1. when $N<{\lambda }_{\mathit{In}}^{-2}<{\lambda }_{\mathit{As}}^{-2}$ the fluxes of both types of growth species to a QD are given by the corresponding diffusion lengths ${\lambda }_{\mathit{As}}$ and ${\lambda }_{\mathit{In}}$ (as illustrated in Fig. 2b). Therefore, the flux ratio $F_{\mathit{As}}/F_{\mathit{In}}={({\mathrm{\Lambda }}_{\mathit{In}}/{\mathrm{\Lambda }}_{\mathit{As}})}^2$ delineates the In-rich (As-limited) regime from the As-rich (In-limited) one. This boundary is shown by the gray dashed line in Fig. 2a.

2. when ${\lambda }_{\mathit{In}}^{-2}<N<{\lambda }_{\mathit{As}}^{-2}$ the As collection is limited by ${\lambda }_{\mathit{As}}$ while the In collection - by $l$ (see Fig. 2c). Thus, the boundary between two regimes is given by $N={\mathrm{\Lambda }}_{\mathit{As}}^{-2}{F}_{\mathit{In}}/F_{\mathit{As}}$, shown by the green dotted line in Fig. 2a. Therefore, the As-limited growth is expected for low V/III ratios and QD surface densities within the blue-shaded region in Fig. 2a.

3. when $N>{\lambda }_{\mathit{As}}^{-2}>{\lambda }_{\mathit{In}}^{-2}$, both As and In collection lengths are limited by the distance between QDs and ${\mathrm{\Lambda }}_{\mathit{In}}={\mathrm{\Lambda }}_{\mathit{As}}=l$. Thus, the limiting type of growth species is the one with the minimal precursor flux ratio (in the assumption of complete pyrolysis). However, at very low V/III ratios segregation of In in droplets can be observed, therefore it is typically avoided for the SK QD growth. So, we consider here V/III ratios above 1 and therefore for high QD density the growth regime is always considered to be limited by In.

Figure 3a illustrates the variation of the QD surface density with the thickness of additionally deposited InAs layer in the cases of In-limited (V/III ratio of 50) growth and transition from As-limited to In-limited regimes (V/III ratio of 5). Solid lines show the model fit to experimental data. In the As-limited regime we assume that the nucleation of new QDs slows down considerably as soon as its surface density is large enough to limit the collection of In¹⁶. In this case we consider the growth of QDs to initiate in the As-limited regime and then proceed in the In-limited regime after the end of the nucleation phase. Therefore, we model the corresponding part of dependence with the constant QD surface density corresponding to the transition from As-limited to In-limited regimes.

Fig. 3.

(a) Variation of QD surface density with the thickness of deposited InAs layer for V/III ratio of 5 and 50. (b) Calculated QD surface density as the function of InAs layer thickness and V/III ratio.

Fitting in this way the dependences of surface density N on the InAs layer thickness h (Fig. 3a) and on V/III ratio (Fig. 2a) simultaneously using the model given by eq. (2) yields $\mathrm{\Gamma }=8.5\pm 0.9$, $h_{\mathit{eq}}=0.5\pm 0.1$, $h_c=1.5\pm 0.1$, $n=(1.9\pm 0.2)\times {10}^{11}{\text{cm}}^{-2}$ in the In-limited regime, and $n=(7.6\pm 0.7)\times {10}^{13}{\text{cm}}^{-2}$ in the As-limited regime. Where the uncertainties are given by fit errors rounded to the first significant figure. The obtained set of parameters allows surface density estimation for a wider range of of V/III ratios and InAs layer thicknesses Figure 3b shows the color map for QD surface density calculated for V/III ratios from 1 to 100 and InAs layer thicknesses between 0.5 and 2 on top of the In(As,P) layer. One can note the sharp decrease in the QD density with the increase of V/III ratio around 20 which we associate with the As-limited nucleation regime which is specific for near-critical QDs formed at $h$ below 1 ML.

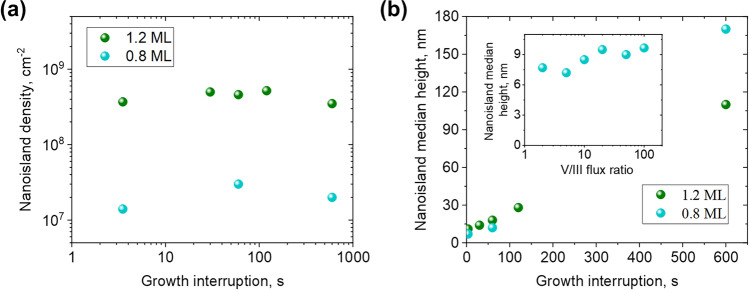
Growth interruption

For an arbitrary thickness of the InAs layer, we vary the duration of the growth interruption to further tune the properties of the QDs. The V/III ratio in these experiments was fixed to 50. Figure 4a shows the saturation of QD surface density as a function of the duration of the growth interruption. After deposition of 1.2 ML of InAs on top of the In(As,P) layer, the QD surface density remains around $(4\pm 2)·{10}^8{\text{cm}}^{-2}$ for all the growth interruptions up to $600\text{s}$. Deposition of slightly less of InAs ($h=0.8$ MLs) results in order of magnitude lower QD densities saturated around $(2\pm 1)·{10}^7{\text{cm}}^{-2}$.

Fig. 4.

Surface density (a) and median height (b) of QDs as the functions of growth interruption duration after additional deposition of 0.8 and 1.2 ML of InAs. The inset in (b) shows the variation of QD density with V/III ratio.

While the surface density saturates, the height of the nanoislands increases with the duration of growth interruption as shown in Fig. 4b. We observe the increase of the median nanoisland height from 11 to 170 nm at $h=0.8$ ML and from 11 to 110 nm at $h=1.2$ ML with the increase of growth interruption from $4\text{s}$ to $600\text{s}$.

Therefore, the size of low-density InAs islands can be controlled in a wide range without significant variation in surface density by tuning the duration of growth interruption. Importantly, the height of QDs changes from $7\text{nm}$ to $10\text{nm}$, despite the two orders of magnitude variation of the QDs density with V/III ratio, as shown in the inset of Figure 4b.

Optical properties of the QD system

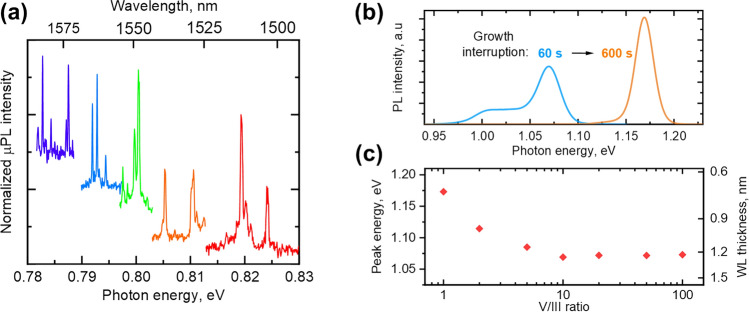
In $\mathrm{\mu }$PL and macro-PL experiments we investigate the low-density QDs ($3·{10}^8{\text{cm}}^{-2}$) grown at V/III ratio of 50 and $h=1.2$ ML. The details of $\mathrm{\mu }$PL and macro-PL are given in the Methods section. In the $\mathrm{\mu }$PL studies of the samples with the growth interruption of $4\text{s}$, we observe the series of well-isolated lines corresponding to emission from single QDs in the spectral range of $1500-1585\text{nm}$, overlapping with the telecom C-band. Figure 5a shows the spectra of individual QDs acquired at $5\text{K}$ and the optical pumping of  $\sim 1\mathrm{\mu }\text{W}$ (beam spot diameter of  $\sim 2\mathrm{\mu }\text{W}$).

Fig. 5.

(a) Low temperature $\mathrm{\mu }$PL spectra of QDs acquired at $5\text{K}$. (b) PL spectra of WL after 60 and $600\text{s}$ of growth interruption. (c) Measured energy of ${\text{InAs}}_x$ ${\text{P}}_{1-x}$ WL peak as the function of V/III ratio for near-critical QDs. The right axis shows the corresponding WL thickness calculated for x = 0.75.

In macro-PL measurements with a laser beam spot of approximately $\sim 200\mathrm{\mu }\text{m}$ in diameter, only the PL signal from the WL is observed. The higher density of states in the two-dimensional WL compared to zero-dimensional QDs results in a significantly higher number of excitons recombining in the WL, making it the dominant contributor to the PL spectrum. Consequently, the PL emission is primarily due to carrier recombination in the WL.

WL peak energy in macro-PL measurements increases with the length of the growth interruption. Figure 5b shows a shift of the WL PL peak from $\sim 1.07\text{eV}$ to $\sim 1.17\text{eV}$ as the growth interruption changes from 60 to $600\text{s}$. The observed peak shift towards higher photon energies at longer growth interruptions is consistent with the model assumption of thinning of the WL during the growth of the nanoislands.

Figure 5c illustrates the variation of the WL PL peak energy measured for the series of samples grown at different V/III flux ratios. We observe the decreasing dependence at V/III ratios below 5 and saturation around $\sim 1.07\text{eV}$.

To quantify the observed changes of the PL signal, we calculate the energy of WL ground state transition (single-particle states) as a function of its thickness using the eight-band $\mathit{k}·\mathit{p}$ method in the nextnano software ⁴¹. The WL is modeled as a homogeneous ${\text{InAs}}_x$ ${\text{P}}_{1-x}$ quantum well at $5\text{K}$ with $x=0.75$ according to our TEM measurements.

The results of 8 $\mathit{k}·\mathit{p}$ calculations allow us to translate the measured values of peak energy to the estimated WL thickness (data on the right axis in Fig. 5c). As the WL peak position remains constant at V/III ratios above 5, it corresponds to saturation of the WL composition and thickness estimated to 4 MLs. At V/III ratios below 5, the WL peak is shifted to higher energies corresponding to either lower WL thickness (down to 2 MLs) or lower As concentration. This is consistent with the decrease of the QDs surface density (or even the absence of them) at V/III = 2 or lower.

Conclusions

We report our method of the formation of highly controllable low-density arrays of InAs/InP QDs via a near-critical nucleation process followed by In flux interruption under the growth temperature. With this approach, we have demonstrated how the surface density and mean size of QDs can be tuned almost independently from each other. Specifically the QD density can be tuned between ${10}^7$–${10}^9$ ${\text{cm}}^{-2}$ by choosing the V/III ratio between 2 and 100.

Methods

Epitaxial growth

All samples were grown in a low-pressure metal-organic vapor phase epitaxy (MOVPE) Turbodisc reactor on InP wafers with (001) orientation. ${\text{H}}_2$ was used as the carrier gas, trimethylindium (TMIn) as the In source, phosphine (${\text{PH}}_3$), tertiarybutylphosphine (TBP), and arsine (${\text{AsH}}_3$) were used as precursors of the V^th group. After thermal deoxidation of the InP(001) substrate at ${650}^{\circ }\text{C}$ in ${\text{PH}}_3$ ambient, the temperature was decreased to ${610}^{\circ }\text{C}$ and a $0.5\mathrm{\mu }\text{m}$-thick InP buffer layer was deposited. Then the temperature was reduced to ${485}^{\circ }\text{C}$ for QD growth under ${\text{PH}}_3$ with following annealing in ${\text{AsH}}_3$ ambient prior to InAs deposition. After the InAs deposition, we use the TMIn flux interruption while keeping the ${\text{AsH}}_3$ flux constant to tune the QDs formation. This step is referred in the text as “growth interruption”. Then, the QD array was first covered with a $10\text{nm}$-thick InP layer using TMIn and TBP sources. Then the temperature was raised to ${610}^{\circ }\text{C}$ for further growth of the InP layer. Then the layer of surface QDs was grown under conditions identical to the buried ones but without InP capping layers.

Morphology and composition studies

The morphology of buried In(As,P) layers and InAs/InP QDs was studied by means of high-angle annular dark-field scanning transmission electron microscopy (HAADF STEM)⁴² using an FEI TEM instrument equipped with a field emission electron gun and aberration correction on the probe forming lenses. The surface (non-buried) QDs density and QDs heights were investigated using the atomic force microscopy (AFM) Bruker Icon system operated in a tapping mode. Typical AFM images are given in Supplementary Information, Fig. S1. For each sample multiple $5\times 5\mu m$ AFM scans were analyzed using Gwyddion software⁴³. In the analysis individual QDs were identified and counted using the grain analysis. The QD surface densities were obtained by dividing the total number of QDs by the total area of the scans.

Optical studies

For the optical experiments, the structures were kept in a helium-flow cryostat with temperature control in the range of $5-300\text{K}$ and pumped non-resonantly with a continuous-wave semiconductor laser diode line at ${\lambda }_{\text{exc}}=640\text{nm}$. For high spectral and micrometer spatial-resolution photoluminescence ($\mathrm{\mu }$PL), the structures were optically excited through an infinity-corrected, high numerical aperture ($\text{NA}=0.4$) objective with $20\times$ magnification, focusing the laser spot to a diameter of $\sim 2\mathrm{\mu }\text{m}$. For macro-PL we used a lens focusing the laser beam to a $\sim 200\mathrm{\mu }\text{m}$ spot diameter. The same objective or lens was used to collect the PL response and direct it for spectral analysis to a $0.3\text{m}$-focal-length monochromator equipped with a liquid-nitrogen-cooled InGaAs multichannel array detector, and with a single-channel InAs detector measuring the macro-PL signal with the lock-in technique.

Author contributions

P.H., Y.B., A.S., and E.S. performed the epitaxial growth of the samples. Y.B. and P.H. performed AFM measurements. S.K. performed TEM sample preparation and measurements. J.M.S., P.H. and M.S. contributed with PL measurements, P.H. performed 8-band k.p calculations, Y.B., A.F. and K.Y. analyzed the data with input from all authors. Y.B. developed the QD growth model. Y.B., P.H., S.K. and E.S. wrote the manuscript with extensive input from all authors. E.S. conceived and supervised the project.

Data avaliability

The data that supports this work is available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-70451-1.