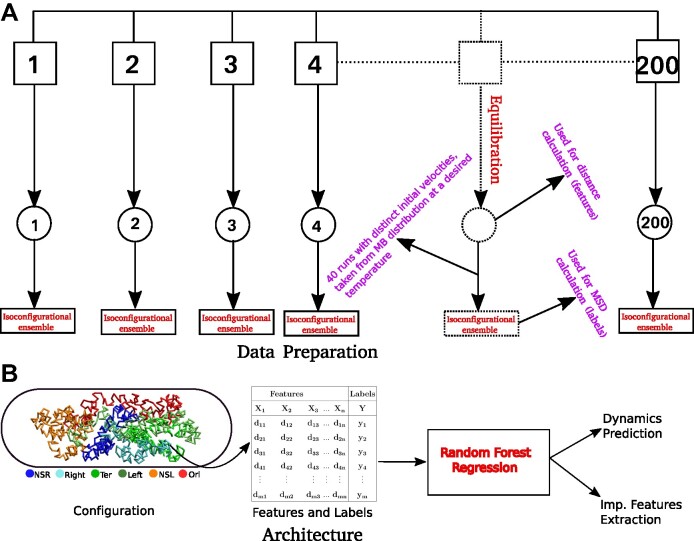
Figure 3.

Schematic representation of the Data preparation and the architecture of Random Forest (RF) regression model. (A) Data Preparation: At the very beginning we generated a set of 200 distinct initial configuration of DNA using bead-in-a-spring polymer model. We ran the Brownian dynamics simulation for each configuration for a time span of 10³τ_BD,to ensure proper equilibration. Following equilibration, pairwise distances were computed using the last snapshot of each run (totaling 200), serving as features for our machine-learning model. For the MSD measurement, we simulate each equilibrium configuration 40 times through Brownian dynamics simulations, drawing distinct velocities from the Maxwell–Boltzmann distribution at a desired temperature of k_BT = 1.0. These ensemble (40 trajectory each) are called iso-configurational ensembles. (B) Architecture: We utilized the pair wise distance between beads and MSDs of each bead. These two quantities serves as features and labels respectively, in our ML model(RF). After training of the Random Forest (RF) with this datasets, we predicted the dynamics of individual beads. For training and testing, 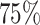and 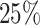of the total datasets, were used. Additionally, from the trained model, we extracted important features contributing to the maintenance of dynamical properties.