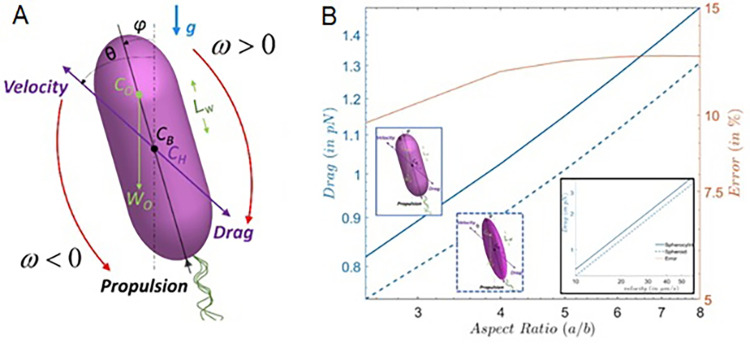
Fig 2. Mechanics of C. okenii swimming.
(A) Schematics of the cell-level geometry for the formulation of the reduced-order model. The free-body diagram of all forces and torques (about point CB) are color marked on the schematics. The swimming of the bacteria cell is considered to be stable when the cell rotates such that its pusher-type propulsion will propel the cell against gravity, g (in the above configuration, this is achieved for ω > 0). The weight and buoyancy forces act opposite to each other, to give an effective weight, (ρcell–ρfluid)Vg, where ρcell and ρfluid respectively denote the cell and surrounding fluid densities, V is the cell volume, g is the acceleration due to gravity (acting downward, in the plane of the Fig). (B) Comparison of drag forces between spherocylinder and spheroid cell geometries for different cell aspect ratios. The y-axis on the right shows the error between the two estimations. For spheroid, the aspect ratio is the ratio between the minor axis and the major axis. For spherocylinders, the aspect ratio is the ratio between the radius of the spherical cap and half of the length of the central cylinder and radius of the spherical caps combined. The maximum error lies below ~11% for the two values. Alternative calculation of the spherocylinder aspect ratio can yield lesser error values (see S6 Text and S4 Fig in S1 File). Inset plot shows the drag force as a function of the swimming velocities.