Improved survival prediction for kidney transplant outcomes using artificial intelligence-based models: development of the UK Deceased Donor Kidney Transplant Outcome Prediction (UK-DTOP) Tool

Abstract

The UK Deceased Donor Kidney Transplant Outcome Prediction (UK-DTOP) Tool, developed using advanced artificial intelligence (AI), significantly enhances the prediction of outcomes for deceased-donor kidney transplants in the UK. This study analyzed data from the UK Transplant Registry (UKTR), including 29,713 transplant cases between 2008 and 2022, to assess the predictive performance of three machine learning models: XGBoost, Random Survival Forest, and Optimal Decision Tree. Among these, XGBoost demonstrated exceptional performance with the highest concordance index of 0.74 and an area under the curve (AUC) consistently above 0.73, indicating robust discriminative ability and calibration. In comparison to the traditional Kidney Donor Risk Index (KDRI), which achieved a lower concordance index of 0.57, the UK-DTOP model marked a significant improvement, underscoring its superior predictive accuracy. The advanced capabilities of the XGBoost model were further highlighted through calibration assessments using the Integrated Brier Score (IBS), showing a score of 0.14, indicative of precise survival probability predictions. Additionally, unsupervised learning via k-means clustering was employed to identify five distinct clusters based on donor and transplant characteristics, uncovering nuanced insights into graft survival outcomes. These clusters were further analyzed using Bayesian Cox regression, which confirmed significant survival outcome variations across the clusters, thereby validating the model’s effectiveness in enhancing risk stratification. The UK-DTOP tool offers a comprehensive decision-support system that significantly refines pre-transplant decision-making. The study’s findings advocate for the adoption of AI-enhanced tools in healthcare systems to optimize organ matching and transplant success, potentially guiding future developments in global transplant practices.

What was known

• Prior models for predicting outcomes in organ transplantation have limited discriminative and calibration power, highlighting a need for improved prediction tools that can better guide clinical decision-making.

• Differences in healthcare systems and data collection methodologies challenge the development of universally applicable predictive models for kidney transplantation outcomes.

• There’s a recognized need for region-specific predictive models that take into account local healthcare practices and patient demographics to enhance transplant outcomes.

This study adds

• The development of the UK-DTOP model using artificial intelligence to predict deceased donor kidney transplant outcomes in the UK, showcasing superior discriminative performance and calibration compared to existing models.

• Insights into the challenges of creating a universal risk calculator for organ transplantation due to significant differences between healthcare systems in the US and the UK.

• Evidence that machine learning techniques can effectively use regional transplant registry data to predict transplantation outcomes, potentially applicable across Europe.

Potential impact

• Advancement in Predictive Models: Demonstrates the superiority of the UK-DTOP, an AI-enhanced predictive model, over traditional models like the KDRI, advocating for a shift toward advanced, data-driven tools in organ transplantation decision-making.

• Global Policy Influence: Encourages the adoption of similar AI-based tools across healthcare systems worldwide, potentially standardizing and improving transplant success rates globally.

• Region-Specific Adaptation: Supports the development of predictive models tailored to local healthcare practices and demographics, increasing the relevance and effectiveness of transplant outcomes.

• Optimization of Transplant Processes: Utilizes sophisticated machine learning techniques to refine donor-recipient matching and organ allocation, optimizing the use of available organs and enhancing transplant success.

• Life-Saving Potential: By improving the accuracy of transplant outcome predictions and optimizing resource allocation, AI-driven models like the UK-DTOP can significantly increase the efficacy of transplants and save more lives.

Introduction

Kidney transplantation offers superior survival and quality of life compared to other alternatives of kidney replacement therapy [1]. However, there is an increasing disconnect between the number of patients in need for kidney transplants and the supply of available organ grafts. Matching the expected graft survival with the patients’ life expectancy as precisely as possible is an intuitive approach to minimize wastage of a very precious resource [2].

Numerous models for predicting kidney graft risk have been published to date to assist evidence-based decision-making [3,4]. The Kidney Donor Risk Index (KDRI), developed by Rao et al. in 2009, is now extensively utilized in clinical decision-making [3,5]. However, KDRI scoring displays a marginal discrimination (C-index = 0.62) to predict between longer and shorter surviving grafts, identifying a major knowledge gap in the deceased-donor transplantation process.

Watson et al. [6] undertook a critical reexamination of the UK Transplant Registry (UKTR) in order to further discern donor factors associated with less favorable transplant outcomes in the UK. Based on their research, they created a simplified donor risk indicator, UK-KDRI, similar in predictive power to the US equivalent but simpler, being based on five donor characteristics rather than the fifteen used for US-KDRI.

Both the US and the UK-KDRIs were trained and tested on transplant patient cohorts from between 1995 and 2007 [3,6], reflecting the immunosuppressive practices and statistical and computing limitations of the era.

Machine learning, fostered by the increasing availability of large datasets easily extracted from electronic data platforms, has been being developed quickly over the past several years and is now utilized in several medical diagnostic disciplines [7–9]. Furthermore, the cutting-edge statistical and machine-learning techniques can generate more precise forecasts [10]. The significance of machine learning-based risk prediction models in medical decision-making was recently emphasized by a systematic study of kidney transplants [11]. Our primary aim was to build a machine learning model to predict deceased donor kidney transplant outcome using a large, multicenter set of data from the UKTR and to assess the model’s performance in comparison to the current benchmark UK-KDRI. In addition to improving predictive accuracy for kidney transplant outcomes using artificial intelligence (AI), our secondary aim was to explore the potential of unsupervised machine learning techniques to cluster and identify patterns within donor and transplant-related factors independently of recipient characteristics. This analysis allowed us to discern inherent groupings or associations that could inform more targeted approaches in donor selection and transplant strategies, potentially leading to enhanced matching protocols and outcomes. By isolating donor and transplant factors, this approach sought to uncover the intrinsic properties of the organs and surgical variables that contribute to transplant success, independently of the recipient’s profile.

Methodology

Study cohort

The UKTR database, a publicly available de-anonymized information repository served as the data source. We analyzed data submitted to the UKTR held by NHS Blood and Transplant. The registry records mandatory data supplied by the 23 adult UK kidney transplant centers. All deceased-donor kidney transplant recipients listed in the UKTR database from 1 January 2008 to 12 January 2022 were included and the outcomes were assessed until 31 May 2023. The maximum duration of follow-up was 16 years. We chose the start date of 2008 for our cohort population due to the relative homogeneity and stability of transplant immunosuppression since. Similarly, standardized molecular methods for HLA typing have been in place for the same period [12,13]. Recipients under 18, ABO-incompatible recipients, recipients with positive flow cytometry positive crossmatch transplants or those who had missing survival data were excluded. The hierarchy for applying inclusion and exclusion criteria is further shown in Figure 1.

Figure 1.

Hierarchy of cohort selection.

Outcomes

Primary outcome was overall graft survival. Starting from the transplantation date forward, time to overall graft failure was the primary result. Overall graft survival was defined as graft loss or patient death. Patients were censored at the end of follow-up period (31 May 2023).

We only took into account independent variables that were reported in the UKTR for all patient groups and characteristics that were known prior to transplantation. For pre-transplant decision-making, our objective was to create a risk index. The traits of the donors and recipients were among the independent variables available in the UKTR database.

These potential independent variables in the UKTR database were examined to ascertain clinical relevance by two independent nephrologists (HA and NK) and a clinical scientist (DB). At least two of the three participants have had to concur in order to include a variable in the model [13,14]. Table 1 of the supporting information shows these variables.

Table 1.

Baseline characteristics and factors included in the final model: a comparison between the training and the validation groups.

	Training group (n = 23,770)	Test group (n = 5943)
Recipient factors
Cause of renal failure: n (%)
Diabetes/hypertension:	5463 (22.98%)	1340 (22.55%)
Glomerulonephritis/vasculitis:	4768 (20.06%)	1175 (19.77%)
Cancer:	127 (0.53%)	39 (0.66%)
Congenital:	4707 (19.80%)	1148 (19.32%)
Unspecified:	8566 (36.04%)	2211 (37.20%)
Vascular:	139 (0.58%)	30 (0.50%)
Recipient age: mean (standard deviation):	51.18 (13.50)	51.15 (13.40)
Pediatric at registration: n (%)
-No:	18,958 (79.76%)	4768 (80.23%)
-Unknown:	4728 (19.89%)	1154 (19.42%)
-Yes:	84 (0.35%)	21 (0.35%)
Recipient weight in kg: mean (standard deviation):	77.24 (21.97)	77.43 (20.86)
-Missing data (n%):	93 (<1%)	257 (4.32%)
Recipient height in cm: mean (standard deviation):	169.59 (22.20)	170.63 (31.65)
-Missing data (n%):	5189 (21.80%)	1256 (21.13%)
Recipient body mass index in kg/m2: mean (standard deviation):	26.73 (4.78)	26.70 (4.72)
-Missing data (n%):	5316 (22.36%)	1283 (21.58%)
Recipient ethnicity: n (%)
White:	17,221 (72.45%)	4305 (72.44%)
Asian:	3539 (14.89%)	869 (14.84%)
Black:	2035 (8.56%)	515 (8.67%)
Other:	775 (3.26%)	200 (3.37%)
Not reported:	200 (0.84%)	54 (0.91%)
Waiting time in days: mean (standard deviation):	1005.717 (857.78)	979.74 (805.95)
-Missing data (n%):	118 (<1%)	24 (<1%)
Dialysis at registration: n (%):
Hemodialysis:	11,468 (48.37%)	2861 (48.28%)
Peritoneal dialysis:	4069 (17.16%)	995 (16.79%)
Not on dialysis:	8018 (33.82%)	2033 (34.31%)
Unknown:	153 (0.65%)	37 (0.63%)
Graft number: n (%)
One:	20,401 (85.82%)	5154 (86.72%)
Two:	2834 (11.92%)	678 (11.41%)
Three:	463 (1.95%)	103 (1.73%)
More than three:	70 (0.31%)	8 (0.13%)
Donor factors
Donor age: mean (standard deviation):	49.41 (16.14%)	49.77 (15.99)
Donor height in cm: mean (standard deviation):	170.30 (11.78)	170.18 (12.03)
Donor weight in kg: mean (standard deviation): -Missing data (n%):	78.04 (18.65) 22 (<1%)	77.86 (18.53) 8 (<1%)
Donor body mass index in kg/m2: mean (standard deviation):	26.66 (5.44)	26.62 (5.47)
-Missing data (n%):	185 (<1%)	45 (<1%)
Donor urine output in the last 24 h in milliliters: mean (standard deviation):	2800.30 (1678.61)	2785.45 (1629.68)
-Missing data (n%):	8502 (35.76%)	2131 (35.85%)
Donor urine output in the last hour in milliliters: mean (standard deviation):	112.68 (111.10)	111.68 (119.35)
-Missing data (n%):	518 (2.1%)	140 (2.3%)
Donor creatinine in mmole/litre: mean (standard deviation):	81.38 (55.18)	81.83 (56.58)
-Missing data (n%):	1091 (4.5%)	260 (4.3%)
Donor history of hypertension: n (%)
No:	16,987 (71.63%)	4205 (70.97%)
Yes:	6300 (26.57%)	1620 (27.34%)
Unknown:	483 (2%)	118 (1.69%)
Donor history of smoking: n (%)
No:	10,552 (44.50%)	2633 (44.44%)
Yes:	12,984 (54.75%)	3254 (54.92%)
Unknown:	178 (0.75%)	38 (0.64%)
Donor amount of smoking: mean (standard deviation)	16.36 (12.64)	16.33 (12.46)
Transplant factors
HLA A mismatch: n (%)
0:	4679 (19.69%)	1105 (18.59%)
1:	11,496 (48.38%)	2912 (49%)
2:	7538 (31.72%)	1916 (32.24%)
Unknown:	57 (0.21%)	10 (0.17%)
HLA B mismatch: n (%)
0:	3906 (16.44%)	910 (15.31%)
1:	15,433 (64.95%)	3920 (65.96%)
2:	4,374 (18.41%)	1103 (18.56%)
Unknown:	57 (0.21%)	10 (0.17%)
HLA DR mismatch: n (%)
0:	10,097 (42.49%)	2528 (42.54%)
1:	11,605 (48.84%)	2883 (48.51%)
2:	2011 (8.46%)	522 (8.78%)
Unknown:	57 (0.21%)	10 (0.17%)
Match points: mean (standard deviation):	6.01 (2.37)	5.97 (2.38)
-Missing data (n%):	162 (<1%)	30 (<1%)
Matchability band: mean (standard deviation):	103.44 (105.21)	105.63 (105.84)
-Missing data (n%):	162 (<1%)	30 (<1%)
Calculated reaction frequency: mean (standard deviation):	21.88 (34.25%)	20.58 (19.74%)

A – Supervised learning methods to enhance predictive accuracy

Initial data preparation, variable selection, data set division into training and test datasets, data pre-processing, model training, and model evaluation were the first five steps in the model construction process. Supplementary file 1 explains the basic concepts for using AI in building prediction models.

Step 1: Feature engineering and variable selection

An initial feature engineering was performed on the unprocessed data. Feature engineering is defined as the process of selecting, modifying, and transforming raw data into features that may be applied to supervised learning. More than 70 categories were included in the variable ‘recipient cause of kidney failure’. Eight subgroups were created within these categories for classification purposes: glomerulonephritis/vasculitis, cancer, congenital, unknown, obstructive, vascular, and hepatic.

Recursive feature elimination (RFE) with eXtreme Gradient Boosting (XGBoost) was used to identify each feature’s variable importance score (VIS) and the best set of predictors, with Harrell’s C-Statistic serving as the performance metric [15]. The key reason for using XGBoost for RFE was its capacity to account for missing values for both continuous and categorical independent variables. Variables with low VIS ratings (<0.002) were left out of the initial dataset. This value was chosen because variables beyond it had no further influence on prediction. The categorical variables’ rows with missing data were tagged ‘unknown’. The continuous variables’ missing data were not removed from the rows that included them.

Step 2: Splitting the data into training and test datasets):

In step 2, the complete dataset was randomly split into training and test datasets. The three predictive models were built using a training set that contained 80% of the data. The forecasting accuracy of each model was rigorously examined using the test set.

Step 3: Data pre-processing:

We performed one-hot encoding for the categorical variables. For each absolute number, one-hot created a new category column and assigned a binary value of 1 or 0. A binary vector with the values 0 and 1 is used to represent each integer value.

Step 4: Model development:

Three different machine-learning models were tested. For hyper-parameter adjustment, each model performed a ten-fold cross-validation:

• Optimal survival tree [16]: The branches of a survival tree are independent variables that influence the time of the occurrence, while the leaves are outcome factors, such as graft failure (1) or no graft failure (0). The complexity parameter, which was set to 0.00001 until the best tree was formed, was used to regularize the minimum number of samples required in a node for a split to be tried and the quantity of competing splits retained in the output.

• Random survival forest model [17]: random survival forest is an ensemble method that uses bootstrap aggregation to create a large number of unpruned survival trees. Hyperparameter tweaking was done for the number of trees, splitting rule selection, number of nodes, and number of variables to divide at each node in order to obtain the minor out-of-bag prediction error.

• XGBoost [18]: XGBoost is a fast gradient-boosting approach that speeds up convergence by taking advantage of the second-order partial derivative of the loss function.

Step 5: Model evaluation:

We used the 20% test set to evaluate the forecasting performance of the models. Our main metric for assessing the accuracy of our predictions was the C-statistic [17]. The C-statistic assesses discrimination and whether the model correctly identifies subjects who experience the outcome as having a higher projected risk than those who do not. The C-statistic was specifically computed using the area under the receiver operating characteristic curve (AUROC) for binary results and Harrell’s concordance for time-to-event outcomes. For calibration assessment, the integrated Brier score (IBS) was employed. We also plotted the actual and expected survival probability at various post-transplant time points.

Step 6: Comparison between our best-fit model and the UK-KDRI:

We used the difference in AUC between our best-fit model and the UK-KDRI to indicate a significant difference in terms of discrimination with a cutoff greater than 0.05 [18,19]. An AUC of less than 0.5 was identified as unreliable. An AUC of 0.7 to 0.8 was regarded as a good model, while 0.8 and higher was deemed excellent [18,19].

Step 7: Model fairness and potential clinical utility:

To gauge the fairness of the model across patients with varying access to health facilities, we divided the test dataset into two subcategories using their relative deprivation scores. The initial group comprised 50% of the more deprived patients, while the second group comprised the remaining 50% who were less deprived. We then reassessed the model’s performance across both sets. We performed decision curve analysis (DCA) in order to assess the potential clinical utility.

B – Unsupervised machine learning analysis

As part of our secondary aim, we utilized the kmeans clustering algorithm in Stata to analyze the donor and transplant factors. We conducted this analysis using the xi: cluster kmeans command, which allowed us to perform k-means clustering on the selected variables. This technique helped us to identify distinct clusters within the data, which represented unique patterns and groupings based solely on donor and transplant characteristics, without the influence of recipient factors.

Prior to clustering, we preprocessed the data to ensure optimal input for the algorithm. This involved standardizing the continuous variables to have a mean of zero and a standard deviation of one, and appropriately handling any missing data to maintain the integrity of the analysis. We then determined the optimal number of clusters by evaluating the within-cluster sum of squares (WCSS) across a range of potential cluster sizes and choosing the number that provided a meaningful segmentation without overfitting.

The results of this clustering provided insights into the inherent associations between donor and transplant variables, offering a novel perspective on how these factors alone could influence transplant outcomes.

Ethics

Data release was granted by the UK Transplant Registry. The Research Governance Department at the University Hospitals of Coventry and Warwickshire in the United Kingdom examined the work. The research was not included in the review by the NHS Research Ethics Committee (REC) because it utilized previously gathered non-identifiable data, including research done by team members of a care facility using data collected while providing care for patients or clients. The reference for the study was GF5005. Ethical approval was provided by Coventry University (reference number P139694) and University Hospitals of Coventry and Warwickshire (reference number GF5005).

Results

Following the application of the inclusion and exclusion criteria, 29,713 patients in total (23,770 in the training dataset and 5943 in the test dataset) were included in the study. The selection structure for the study cohort is shown in Figure 1. The number of independent variables available before transplant was 91. After RFE and feature engineering, the independent variables used in our models were further condensed to 26. Supplementary file 2 lists the RFE features and variable importance ratings. Table 1 lists the baseline characteristics of the cohort used for model development.

Results for the supervised learning methods

Discrimination: The random survival forest and the XGBoost obtained the highest concordance indices (0.74). The concordance was lowest (0.70) for the optimal decision tree. The comparison of the three models’ AUC scores at various time points is shown in Table 2. The AUC was highest for the XGBoost model.

Table 2.

Comparison between the 3 decision-based models in terms of AUC score at different time points.

	Optimal decision tree	Random survival forest	XGBOOST
Year 1	0.68	0.72	0.72
Year 2	0.70	0.73	0.73
Year 3	0.71	0.74	0.74
Year 4	0.71	0.74	0.74
Year 5	0.71	0.75	0.75
Year 6	0.71	0.75	0.75
Year 7	0.71	0.74	0.76
Year 8	0.71	0.74	0.75
Year 9	0.70	0.73	0.75
Year 10	0.69	0.72	0.73

The bold values are the highest values among in the comparison.

Calibration

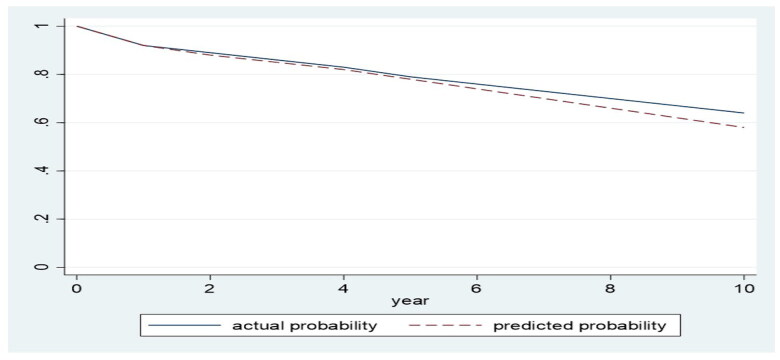
The performance of calibration across several models was evaluated using the IBS. The IBS score for the XGBoost, the random survival forest, and the optimal decision tree models was 0.14 for each model. The actual odds of the XGBoost predictions on survival are plotted in Figure 2. The simplified calibration approach we have used, comparing the predicted survival probabilities from our XGBoost model to Kaplan–Meier estimates, has been specifically chosen to facilitate understanding without compromising the conveyance of essential information about model performance.

Figure 2.

Actual survival probabilities were calculated using the Kaplan-Meier survival product estimator; then the average of these values was calculated at each time point. The average actual survival probabilities were plotted against the equivalent predicted probabilities at different time points.

Selection of the best-fit model

XGBoost fared significantly better than the random survival forest regarding computation time, and slightly better in terms of ranking and calibration performance (as shown in Table 2). It fared significantly better than the optimal decision tree in terms of computation time, ranking, and calibration (as shown in Table 2). Accordingly, XGBoost was selected as the best model that fit the data and, from here, we will refer to it in this paper as UK Deceased-Donor Kidney Transplant Outcome Prediction, or ‘UK-DTOP model for graft survival’. There was no evidence of overfitting or underfitting as the discriminative and calibration metrics in the training and test datasets were similar. The final model configuration included a learning rate of 0.01, a max depth of 6 for each tree, and 100 iterations. These parameters were chosen based on their performance in cross-validation tests, focusing on maximizing the concordance index and minimizing the Brier score for our survival data.

Comparison between the UK-DTOP and the UK-KDRI

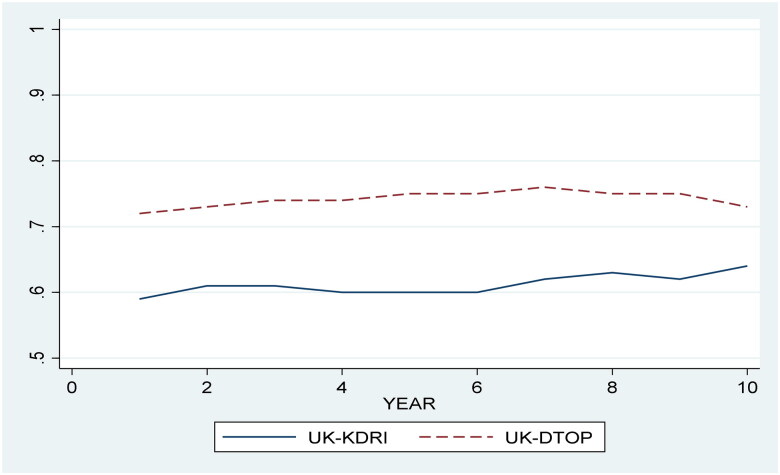
Thereafter, we assessed the UK-KDRI on the same cohort used to develop the UK-DTOP with penalized Cox regression. The model outcome variable was overall graft survival and the only independent variable used in the model was the UK-KDRI score. The concordance of the UK-KDRI was 0.57, while the UK-DTOP had a concordance of 0.64. Table 3 compares the UK-DTOP and the UK-KDRI in terms of AUC score at different time points. Figure 3 displays the AUC scores for both models over time.

Table 3.

Comparison between the UK-DTOP and the UK-KDRI in terms of AUC score at different time points.

Year	UK-KDRI	UK-DTOP
Year 1	0.59	0.72
Year 2	0.61	0.73
Year 3	0.61	0.74
Year 4	0.60	0.74
Year 5	0.60	0.75
Year 6	0.60	0.75
Year 7	0.62	0.76
Year 8	0.63	0.75
Year 9	0.62	0.75
Year 10	0.64	0.73

The bold values are the highest values among in the comparison.

Figure 3.

Comparison between the UK-DTOP and the UK-KDRI in terms of AUC over time.

Subgroup analysis based on deprivation scores

The UK-DTOP (using the XGBOOST model) showed a concordance index of 0.75 when evaluated on the subgroup of patients more deprived and had a concordance index of 0.72 when evaluated on the subgroup of patients who were less deprived. Table 4 shows a comparison between the AUC scores at different time points between both groups.

Table 4.

Evaluation of the AUC scores at different time points across the more deprived and the less deprived groups.

	Most deprived deprived group	Least deprived group
1 year	0.74	0.70
2 years	0.75	0.73
3 years	0.76	0.72
4 years	0.76	0.73
5 years	0.75	0.73
6 years	0.76	0.74
7 years	0.76	0.73
8 years	0.76	0.73
9 years	0.77	0.73
10 years	0.76	0.72

Assessment of potential clinical utility

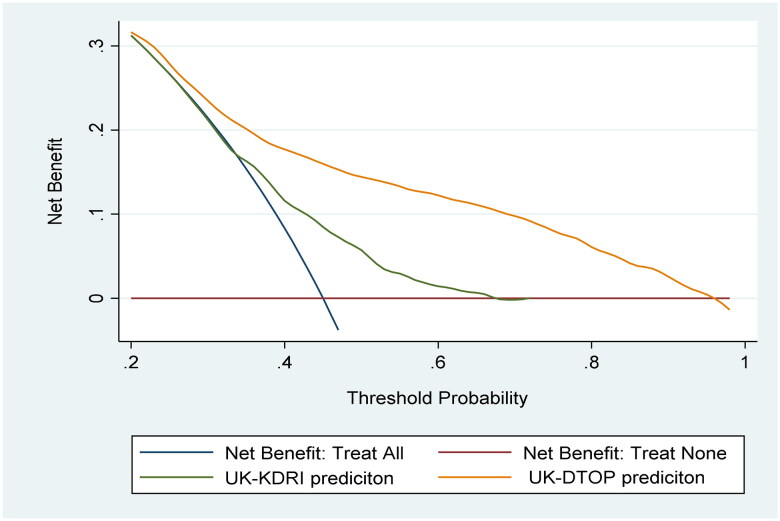
Figure 4 plots the net benefit of using the UK-DTOP in comparison to the UK-KDRI across different thresholds. It also compares it against the theoretical situations of assuming all patients will lose their grafts (treat all) and assuming none will lose their grafts (treat none). Figure 4 shows the superiority of the UK-DTOP.

Figure 4.

Decision curve analysis to assess the potential clinical utility.

Furthermore, to statistically compare the AUROCs of the UK-KDRI and D-TOP models, we employed the bootstrap method. This approach is widely recognized for its robustness in estimating the precision of AUROC comparisons and handling the variability inherent in such estimates [45,46]. This difference was found to be statistically significant, with a p value of less than 0.01.

The URL http://api1.xtend.ai:4930/ provides access to a user-friendly web application that may be used to apply the model for prediction. (Currently, the website is inactive. Once the manuscript is accepted, we intend to launch it). University Hospitals of Coventry and Warwickshire, UK owns the copyrights.

We were interested, from an academic perspective to assess the performance of cox regression model using the same variables used in our UK-DTOP model for graft survival. We used simple imputation to treat the missing data and found that the proportional hazard assumption of the cox regression model was significantly violated, making its predictions unreliable.

Results for the unsupervised learning methods

Upon implementing the k-means clustering algorithm, five distinct clusters were identified within the donor and transplant factors. These clusters represented unique combinations of characteristics, suggesting different profiles of donor and transplant attributes. Details of baseline characteristics of these clusters are shown in Table 5.

Table 5.

Baseline characteristics of the clusters.

	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	p Value
Cause of death						<0.001
CNS tumor	143 (1.37%)	13 (0.92%)	22 (0.55%)	83 (0.62%)	14 (1.78%)
Intracranial-type unclassified (CVA)	420 (4.01%)	54 (3.81%)	80 (2.0%)	471 (3.53%)	39 (4.95%)
anoxia	2325 (22.21%)	287 (20.24%)	617 (15.44%)	5495 (41.17%)	240 (30.46%)
Cerebrovascular/stroke	5646 (53.93%)	739 (52.12%)	3013 (75.4%)	6244 (46.79%)	401 (50.89%)
Other	744 (7.11%)	296 (20.87%)	167 (4.18%)	714 (5.35%)	63 (7.99%)
trauma	1192 (11.38%)	29 (2.05%)	97 (2.43%)	339 (2.54%)	31 (3.93%)
Donor type						<0.001
DBD	8275 (79.04%)	1023 (72.14%)	2115 (52.93%)	6688 (50.11%)	224 (28.43%)
DCD	2195 (20.96%)	395 (27.86%)	1881 (47.07%)	6658 (49.89%)	564 (71.57%)
HLA DQ						<0.001
0	5059 (54.11%)	540 (42.45%)	835 (25.3%)	3653 (32.84%)	206 (30.03%)
1	3740 (40.0%)	630 (49.53%)	1856 (56.24%)	6183 (55.59%)	364 (53.06%)
2	551 (5.89%)	102 (8.02%)	609 (18.45%)	1287 (11.57%)	116 (16.91%)
Sex						<0.001
Female	3878 (37.04%)	807 (56.91%)	1200 (30.03%)	7634 (57.2%)	133 (16.88%)
Male	6592 (62.96%)	611 (43.09%)	2796 (69.97%)	5712 (42.8%)	655 (83.12%)
Blood group						<0.001
unknown	0 (0.0%)	0 (0.0%)	6 (0.15%)	0 (0.0%)	0 (0.0%)
A	2426 (23.17%)	491 (34.63%)	1044 (26.13%)	7677 (57.52%)	514 (65.23%)
AB	154 (1.47%)	249 (17.56%)	202 (5.06%)	345 (259%)	21 (2.66%)
B	503 (4.8%)	130 (9.17%)	1347 (33.71%)	890 (6.67%)	55 (6.98%)
O	7387 (70.55%)	548 (38.65%)	1397 (34.96%)	4434 (33.22%)	198 (25.13%)
Ethnicity						<0.001
Asian	68 (0.65%)	26 (1.83%)	235 (5.88%)	334 (2.5%)	0 (0.0%)
Black	63 (0.6%)	73 (5.15%)	112 (2.8%)	153 (1.15%)	3 (0.38%)
Not reported	35 (0.33%)	21 (1.48%)	42 (1.05%)	117 (0.88%)	0 (0.0%)
Other	118 (1.13%)	38 (2.68%)	199 (4.98%)	333 (2.5%)	4 (0.51%)
Unknown	10 (0.09%)	3 (0.21%)	5 (0.13%)	15 (0.11%)	0 (0.0%)
White	10176 (97.19%)	1257 (88.65%)	3403 (85.16%)	12394 (92.87%)	781 (99.11%)
Donor CMV						<0.001
No	6877 (65.68%)	912 (64.32%)	1419 (35.51%)	5510 (41.29%)	582 (73.86%)
Yes	3451 (32.96%)	493 (34.77%)	2547 (63.74%)	7699 (57.69%)	197 (25.0%)
Unknown	142 (1.36%)	13 (0.92%)	30 (0.75%)	137 (1.03%)	9 (1.14%)
Hepatitis B surface antigen						<0.001
No	10438 (99.69%)	1407 (99.22%)	3976 (99.5%)	13321 (99.81%)	783 (99.37%)
Yes	4 (0.04%)	2 (0.14%)	15 (0.38%)	3 (0.02%)	2 (0.25%)
Unknown	28 (0.27%)	9 (0.63%)	5 (0.13%)	22 (0.16%)	3 (0.38%)
Epstein–Barr virus						<0.001
No	1030 (9.84%)	27 (1.9%)	90 (2.25%)	474 (3.55%)	35 (4.44%)
Yes	6242 (59.62%)	819 (57.76%)	2995 (74.95%)	9428 (70.64%)	585 (74.24%)
Unknown	3198 (30.54%)	572 (40.34%)	911 (22.8%)	3444 (25.81%)	168 (21.32%)
Donor history of diabetes						<0.001
No	9928 (94.82%)	1048 (73.91%)	3705 (92.72%)	12328 (92.37%)	641 (81.35%)
Yes	446 (4.26%)	341 (24.05%)	213 (5.33%)	867 (6.5%)	133 (16.88%)
Unknown	96 (0.92%)	29 (2.05%)	78 (1.95%)	151 (1.13%)	14 (1.78%)
Donor Family history of diabetes						<0.001
No	6055 (57.83%)	505 (35.61%)	1955 (48.92%)	10790 (80.85%)	637 (80.84%)
Yes	4052 (38.7%)	855 (60.3%)	1898 (47.5%)	1791 (13.42%)	77 (9.77%)
Unknown	363 (3.47%)	58 (4.09%)	143 (3.58%)	765 (5.73%)	74 (9.39%)
Donor history of hypertension						<0.001
No	8677 (82.87%)	816 (57.55%)	3246 (81.23%)	8206 (61.49%)	477 (60.53%)
Yes	1597 (15.25%)	560 (39.49%)	624 (15.62%)	4911 (36.8%)	297 (37.69%)
Unknown	196 (1.87%)	42 (2.96%)	126 (3.15%)	229 (1.72%)	14 (1.78%)
Donor history of liver disease						<0.001
No	9938 (94.92%)	1210 (85.33%)	3695 (92.47%)	12591 (94.34%)	548 (69.54%)
Yes	293 (2.8%)	124 (8.74%)	143 (3.58%)	418 (3.13%)	209 (26.52%)
Unknown	239 (2.28%)	84 (5.92%)	158 (3.95%)	337 (2.53%)	31 (3.93%)
Donor history of smoking						<0.001
No	5308 (50.7%)	316 (22.28%)	760 (19.02%)	6767 (50.7%)	162 (20.56%)
Yes	5066 (48.39%)	1078 (76.02%)	3168 (79.28%)	6488 (48.61%)	614 (77.92%)
Unknown	96 (0.92%)	24 (1.69%)	68 (1.7%)	91 (0.68%)	12 (1.52%)
HLA A						<0.001
0	3793 (36.23%)	112 (7.9%)	401 (10.04%)	1424 (10.67%)	103 (13.07%)
1	4645 (44.37%)	642 (45.31%)	2288 (57.27%)	6600 (49.46%)	380 (48.22%)
2	2012 (19.22%)	661 (46.65%)	1297 (32.47%)	5288 (39.63%)	305 (38.71%)
Unknown	18 (0.17%)	2 (0.14%)	9 (0.23%)	31(0.23%)	0 (0.0%)
HLA B						<0.001
0	3298 (31.51%)	82 (5.79%)	188 (4.71%)	1230 (9.22%)	49 (6.22%)
1	6105 (58.32%)	1134 (80.03%)	2144 (53.67%)	9767 (73.2%)	417 (52.92%)
2	1047 (10.0%)	199 (14.04%)	1654 (41.4%)	2315 (17.35%)	322 (40.86%)
unknown	18 (0.17%)	2 (0.14%)	9 (0.23%)	31 (0.23%)	0 (0.0%)
HLA DR						<0.001
0	6737 (64.36%)	798 (56.32%)	825 (20.65%)	4202 (31.49%)	202 (25.63%)
1	3308 (31.6%)	566 (39.94%)	2217 (55.49%)	8126 (60.9%)	415 (52.66%)
2	405 (3.87%)	51 (3.6%)	944 (23.63%)	984 (7.37%)	171 (21.7%)
Unknown	18 (0.17%)	2 (0.14%)	9 (0.23%)	31 (0.23%)	0 (0.0%)
Match grade						<0.001
0	2424 (23.2%)	29 (2.05%)	10 (0.25%)	169 (1.27%)	3 (0.38%)
Favorable	2877 (27.53%)	308 (21.77%)	252 (6.32%)	1715 (12.88%)	58 (7.36%)
Non-favorable	5149 (49.27%)	1078 (76.18%)	3724 (93.43%)	11428 (85.85%)	727 (92.26%)
HLA group						<0.001
1	2424 (23.2%)	29 (2.05%)	10 (0.25%)	169 (1.27%)	3 (0.38%)
2	3838 (36.73%)	641 (45.3%)	440 (11.04%)	3149 (23.66%)	103 (13.07%)
3	3392 (32.46%)	654 (46.22%)	1964 (49.27%)	8123 (61.02%)	405 (51.4%)
4	796 (7.62%)	91 (6.43%)	1572 (39.44%)	1871 (14.05%)	277 (35.15%)
Match points						<0.001
1	292 (2.8%)	54 (3.82%)	116 (2.93%)	641 (4.84%)	19 (2.41%)
2	616 (5.92%)	86 (6.08%)	188 (4.76%)	913 (6.89%)	31 (3.94%)
3	884 (8.49%)	126 (8.9%)	239 (6.05%)	1316 (9.93%)	49 (6.23%)
4	917 (8.81%)	199 (14.06%)	286 (7.24%)	1423 (10.74%)	68 (8.64%)
5	938 (9.01%)	198 (13.99%)	338 (8.55%)	1454 (10.97%)	82 (10.42%)
6	1103 (10.59%)	209 (14.77%)	477 (12.07%)	1659 (12.52%)	102 (12.96%)
7	1573 (15.11%)	202 (14.28%)	640 (16.19%)	2300 (17.36%)	180 (22.87%)
8	1877 (18.03%)	187 (13.22%)	888 (22.46%)	2175 (16.41%)	173 (21.98%)
9	1697 (16.3%)	138 (9.75%)	651 (16.47%)	1183 (8.93%)	74 (9.4%)
10	514 (4.94%)	16 (1.13%)	130 (3.29%)	187 (1.41%)	9 (1.14%)
Age	44.83 (16.65)	49.20 (13.60)	47.13 (14.52)	53.53 (15.32)	54.94 (13.82)	0.000e + 00
BMI	25.93 (5.13)	28.14 (6.29)	26.56 (5.01)	27.07 (5.64)	27.37 (5.54)	1.700e-81
Creatinine	84.91 (56.08)	80.43 (54.91)	84.42 (62.69)	78.23 (53.18)	77.84 (43.97)	5.469e-20
Matchability	104.32 (105.70)	90.51 (93.13)	66.50 (86.03)	115.95 (109.52)	86.93 (80.95)	1.212e-155
CRF	34.79 (40.41)	13.44 (27.35)	16.37 (29.64)	14.75 (27.80)	18.22 (29.69)	0.000e + 00

Following the clustering, we performed univariate Bayesian Cox regression analyses for each cluster to assess their association with overall graft survival.

We employed Bayesian Cox regression, which presents several methodological advantages. First, this approach is inherently more robust for analyzing smaller sample size groups or clusters.

Moreover, Bayesian Cox regression demonstrates superior performance with non-linear data. This flexibility allows us to capture more complex biological interactions and dependencies that may exist among donor and transplant variables, which are often not adequately modeled by traditional linear approaches.

Additionally, Bayesian methods are robust to violations of model assumptions that can adversely affect the results of more conventional regression analyses. By directly incorporating uncertainty into the analysis and allowing for the systematic integration of prior knowledge, Bayesian Cox regression provides a framework that is both adaptable and grounded in clinical realism.

These characteristics make Bayesian Cox regression particularly valuable for medical research, where the accuracy and reliability of statistical analyses are critical for informing patient care and policy decisions.

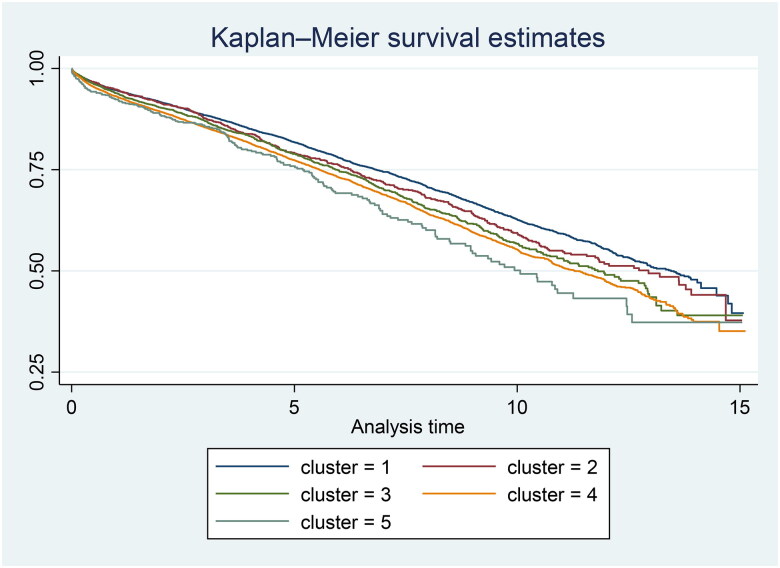
The Bayesian Cox regression analysis revealed significant variations in overall graft survival across the clusters. For instance, certain clusters exhibited significantly better survival rates, indicating a potentially favorable combination of donor and transplant characteristics. Conversely, other clusters showed poorer outcomes, suggesting less optimal donor or transplant conditions. Details of the results of the Bayesian cox regression are shown in Table 6. Kaplan–Meier curves were performed to illustrate the survival probabilities across different clusters (Figure 5).

Table 6.

Comparison between different clusters using Bayesian cox regression.

Cluster	Hazard ratio (Median)	Standard deviation	MCSE	95% Credible interval
1	Reference	–	–	–
2	1.122854	0.0605839	0.002645	1.010174 to 1.25575
3	1.170020	0.0448865	0.001814	1.082837 to 1.265328
4	1.265779	0.0319658	0.001764	1.203567 to 1.331582
5	1.414368	0.1031516	0.004159	1.210496 to 1.62198

Figure 5.

Kaplan–Meier estimates among different clusters.

Discussion

We developed the AI-based UK-DTOP model for graft survival, designed specifically for deceased-donor kidney transplantation in the UK. This novel tool demonstrates superior calibration and discriminative power compared to existing formulas, including the UK-KDRI. Our model significantly outperforms the UK-KDRI, suggesting it can enhance the selection of optimal deceased donors and improve kidney allocation outcomes [6]. Compared to our updated UK-DTOP, which boasts a discriminative power of 0.74, the UK-KDRI trained on outdated patient data and historical immunosuppressive protocols demonstrates relatively inferior discriminative power (0.62) and lower AUCROC scores when applied to current practices. This improvement reflects a robust ability of the model to predict survival, which is a critical aspect in clinical predictive modeling, ultimately resulting in better patient outcomes. It also suggests enhanced donor-recipient matching in kidney transplantation, reducing graft failure rates and increasing survival chances. Additionally, the model’s accuracy sets a new standard, promoting further research and the use of advanced techniques like XGBoost to handle complex data interactions and missing data effectively.

We used DCA to evaluate the practical value of predictive models by comparing net benefits across various threshold probabilities. DCA assesses whether using a model to guide decisions provides more benefit than treating all or treating none. DCA plots net benefit against threshold probabilities, illustrating how model predictions influence decision-making. A well-performing model in DCA offers higher net benefit across thresholds. In survival models, DCA helps assess clinical usefulness by predicting outcomes and guiding treatment decisions. Our UK-DTOP model outperformed UK-KDRI and the all-or-none approaches in predicting graft failure.

Model fairness ensures unbiased functioning of machine learning models, crucial for equitable outcomes, especially in disadvantaged communities. In the UK, where disparities in income and healthcare exist, it is vital to assess model performance across different groups. Evaluating the UK-DTOP model across low and high deprivation subgroups revealed comparable performance, indicating fairness and reproducibility. The UK-DTOP, considering both donor and recipient factors, outperforms UK-KDRI, offering a comprehensive tool for informed decision-making in transplant outcomes.

The UK-KDRI’s dependence on Cox regression models, assuming proportional hazards, presents challenges in medical contexts where this assumption frequently does not hold [17,20–22]. Conversely, our AI-based algorithms provide several advantages: they can utilize precise data without normalization or scaling, avoid proportional hazard assumptions, and are minimally affected by missing values when making predictions [18,23–25]. We opted not to use Cox regression or neural network models with the UKTR data due to their inability to handle missing data without imputation techniques [17,18,21–25]. As the missing data in the UKTR database were ‘missing not at random’, imputation techniques would lead to biased and unreliable predictions [26–29]. Our UK-DTOP model for graft survival employs AI decision-based models that treat missing data as a separate class, unique in handling missing data among continuous variables without requiring imputation techniques [16].

To further elaborate, our UK-DTOP model is a versatile tool for assessing kidney transplant success by considering donor, recipient, and transplant factors. It optimizes donor–recipient matching to maximize graft survival, aiding in decision-making for both single and multiple donor–recipient scenarios. Its accurate calibration enhances doctor–patient communication by providing precise survival probabilities. Ultimately, the decision to accept a kidney offer relies on the recipient’s willingness to accept risk, with the model aiding in quantifying survival probabilities reliably [30]. Patients on the transplant waiting list vary in the number of organ offers they receive and their willingness to accept risks associated with transplantation. Some, burdened by dialysis, are eager for a transplant. Recipients can decline offers due to various subjective reasons, remaining on the list if otherwise relatively healthy. Justifications for refusal include health concerns and doubts about graft longevity. Time constraints often limit patients’ decision-making to an hour or less. [2,3,30–32]. By providing precise graft survival estimates, the UK-DTOP model can alleviate these concerns, potentially increasing acceptance rates. The model’s predictions offer confidence in accepting kidneys for recipients with favorable outcomes, reducing declines due to perceived quality issues. Our UK-DTOP model shows superior performance in predicting overall graft survival compared to the KDRI. By combining graft and patient survival predictions into one model, the UK-DTOP reduces the compounded errors from using multiple models. Although predictive accuracy has inherent limitations, our integrated approach aims to mitigate these, providing a cohesive, data-driven foundation for more accurate predictions. This consolidation highlights the strength of the UK-DTOP model in transplantation, offering a more efficient and precise alternative to current practices.

We chose to assess overall graft survival rather than death-censored graft survival in our UK-DTOP model to comprehensively account for graft loss dynamics and regulatory precedents. Patient deaths account for about 50% of all graft losses, making it crucial to include mortality in transplant outcome evaluations. This approach aligns with U.S. transplantation registries like UNOS, SRTR, and CMS, which use a composite definition of graft loss including both graft function cessation and recipient death, as established by the National Organ Transplantation Act (NOTA) of 1984. Recognizing patient death as a competing risk to graft failure is essential, as death-censored graft survival can lead to biased results. Overall graft survival offers a holistic assessment of transplant program performance, crucial for clinical decision-making and regulatory compliance. It includes direct causes of graft loss like acute rejection, complications, and noncompliance, thus capturing a comprehensive picture of transplant efficacy.

The concern that the calculator might inherently favor recipients with better prognostic profiles, such as younger, non-diabetic individuals, touches on the critical issue of fairness and equity in organ allocation. The UK-DTOP model aims to improve predictive accuracy of transplant outcomes, informing but not dictating decisions. Its goal is to ensure scientifically informed and ethically sound allocation, considering medical and social factors as mandated by policies. To avoid biases and ensure equity, the model should be integrated within a framework respecting justice and broader allocation criteria, including urgency and waiting time. The UK-DTOP enhances the allocation process by providing insights into graft survival, used alongside other tools and criteria. It helps improve the use of scarce donor kidneys by identifying recipients who would benefit most, balancing utility with ethical equity. A proposed tier system could prioritize those in greatest need, maximizing transplant benefits while ensuring fair access.

Regarding donor factors, we identified five distinct donor clusters, each with unique characteristics impacting graft survival outcomes:

1. Cluster 1: Comprised younger donors with the best physiological profiles, averaging 44.83 years in age, lower BMI, and lower creatinine levels. The primary cause of death was cerebrovascular incidents, indicating fewer complications due to the sudden nature of these events.

2. Cluster 2: Slightly older donors with an average age of 49.20 years and higher BMI values, presenting a more varied health landscape. This cluster had more donors who died from anoxia, indicating specific organ viability challenges needing tailored management.

3. Cluster 3: Consisted of the oldest donors with significant health challenges, the highest BMI and creatinine levels, and a substantial proportion of DCD donors. Cerebrovascular deaths were common, requiring specialized transplant strategies due to compounded medical complexities.

4. Cluster 4: Nearly half of the donors were DCD, facing challenges with rapid organ retrieval. Similar to Cluster 3, this cluster had elevated BMI and creatinine levels, necessitating careful handling and innovative transplant approaches.

5. Cluster 5: Featured the most challenging donor profiles with the highest average age, BMI, and creatinine levels. It had the lowest matchability due to significant HLA mismatches and the highest percentage of DCD donors. Donors often had histories of diabetes, liver disease, and smoking, requiring rigorous pre-transplant assessments and highly customized post-transplant care to optimize outcomes.

The identification of a fifth cluster indicates variations in donor and transplant characteristics that the KDRI’s quartile system does not capture. This cluster may represent factors that either mitigate or exacerbate risks in ways the existing four groups do not distinctly classify. For instance, this additional group might include donors with characteristics that pose higher risks or offer potential benefits under-recognized by the KDRI quartiles. By identifying this extra group, our model enhances donor assessment precision, potentially leading to more accurate matching between donors and recipients. This improved matching could result in better graft survival rates, ensuring recipients receive kidneys optimally suited to their medical needs. Additionally, the fifth cluster could refine the allocation process, making it more efficient by better utilizing kidneys that might otherwise be underutilized or misallocated under the current system.

Our UK-DTOP model does have limitations. Variability in reported data, unmonitored recipient traits like biological fragility or cardiovascular risk factors, and missing significant donor characteristics could influence predictions. The registry lacks data on donor-specific antibodies, proteinuria, histological details, high-resolution HLA mismatches, and biomarkers for delayed graft function, all of which are important for long-term outcomes. Despite these limitations, we identified key deceased-donor risk characteristics linked to recipient graft survival and produced an acceptable discrimination index for future organ allocation and decision-making.

Given these limitations, we recommend cautious interpretation of the UK-DTOP model’s predictions, particularly for transplant matching and success enhancement. While validation within the current allocation framework shows its potential as a decision-making tool, further research and methodological innovations are necessary to understand its predictive accuracy in counterfactual scenarios and broader clinical impacts. We stress the need for ongoing research and advanced predictive and causal inference methods to accurately assess the model’s capabilities and constraints. Our k-means clustering analysis identified five distinct donor and transplant factor groups influencing graft survival, compared to the four quartiles used in the current KDRI. This suggests that the current stratification may overlook critical variations in donor profiles that affect transplant success.

In conclusion, our findings suggest that kidney allocation policies should be updated to include more detailed risk stratification. This could lead to advanced models that better account for donor complexity, improve transplant outcomes and aid in better decision-making when accepting organ offers. By taking full advantage of current computing technology, recipients of deceased kidney donor transplants may have improved risk evaluations and the kidney allocation schemes may be employed more efficiently. We acknowledge the insight regarding the comparison with the UK Kidney Allocation System (UK-KAS) rather than the UK-KDRI. Our intention was not to replace the UK-KAS, which balances utility and equity in kidney allocation through a tiered system, but presenting a state-of the art integration of computer science and database research. We referenced the KDRI to benchmark our model’s predictive performance, as KDRI assesses donor-related risks within Tier B of the UK-KAS. We propose incorporating the UK-DTOP as a complementary tool within the UK-KAS to optimize transplant outcomes, ultimately benefiting patients through improved success rates and graft longevity.

Disclaimer

The University Hospitals Coventry & Warwickshire NHS Trust, Coventry, United Kingdom, owns the copyrights to the web application model.

Funding Statement

Partial funding by TOPOL fellowship programme and UHCW charity.

Author contribution

Hatem Ali: Literature search, data collection, design, analysis, and manuscript writing

Arun and Sunil Shroff: web application development, analysis improvement and fine tuning of the final model

Adnan Sharif: Manuscript review, improvement and fine-tuning of analysis

Miklos Z. Molnar: Review and analysis improvement

Karim Soliman: Review and analysis improvement

Bernard Burke: Academic supervision

David Briggs: Academic supervision, manuscript writing and review

Nithya Krishnan: Academic and clinical supervision, manuscript writing and review

Disclosure statement

The authors affirm that they have no competing interests that would prevent this paper from being published. Dr. Soliman is a current employee of the United States Veterans Health Administration. However, the views and ideas represented here do not represent the official views or opinions of and are not endorsed by the United States Veteran Health Administration. I confirm that none of the authors has been involved in the editorial handling or peer review. I confirm that no competing interests to declare.