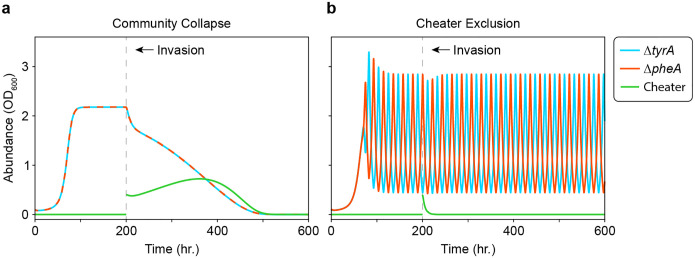
Extended Data Fig. 6. Population cycles from temporal separation of resource production resist invasion and collapse from a metabolic cheater.

Each plot shows the dynamics of $\Delta \mathit{\text{tyrA}}$ (cyan), $\Delta \mathit{\text{pheA}}$ (red), and a cheater (green) in a simulated invasion experiment. The cheater was added as an additional variable in the full model (equation (1)) that competes for glucose and amino acid without producing amino acid. Following an initial period with only $\Delta \mathit{\text{tyrA}}$ and $\Delta \mathit{\text{pheA}}$ in the community, the cheater abundance was reset to 0.4 (OD₆₀₀) and the simulation proceeded. A simplified symmetrical parameter set was used for the simulations (Extended Data Table 1), where the resource consumption quotas for the cheater $q_{3j}$ were equal to those for $\Delta \mathit{\text{tyrA}}$ and $\Delta \mathit{\text{pheA}}$. Since the cheater was defined as a dual auxotroph, the cheater growth rate was set as the minimum over all three resources with a small growth advantage from the loss of biosynthetic burden where ${\mu }_3=1.05\cdot \text{min}\left({\mu }_{31},{\mu }_{32},{\mu }_{33}\right)$. a) Invasion of a community at stable equilibrium with the initial condition $N_1=N_2=0.1,N_3=0,R_3=11.11,R_1=R_2=1$. b) Invasion of a community on its limit cycle with the initial condition $N_1=0.1,N_2=0.11,N_3=0,R_3=11.11,R_1=R_2=1$.