The growing charge-density-wave order in CuTe lightens and speeds up electrons

Abstract

Charge density waves (CDWs) are pervasive orders in solids that usually enhance the effective mass (m*) and reduce the Fermi velocity ($v_{\mathrm{F}}$) of carriers. Here, we report on the inverse — a reduced m* and an enhanced $v_{\mathrm{F}}$ correlated with the growth of the CDW order in CuTe with gapped, practically linearly dispersing bands — reminiscent of emergent CDW-gapped topological semimetals. Using momentum-dependent electron energy-loss spectroscopy (q-EELS), we simultaneously capture m* and $v_{\mathrm{F}}$ of the CDW-related, practically linearly dispersing electrons by plasmon dispersions across the transition (335 K, T_CDW), with m* of 0.28 m₀ (m₀, the electron rest mass) and $v_{\mathrm{F}}$ of ~ 0.005c (c, the speed of light) at 300 K. With the growth of the CDW order-parameter strength toward 100 K, the electrons become lighter and move faster by ~ 20%. Thorough inspection below T_CDW unveils the essential role of the increasing opening of the CDW gap. CuTe is a rich platform for the exploration of CDW/correlation physics with q-EELS established as a useful probe for this type of physics.

Charge density waves usually cause electrons to become heavier and slow down. Here, the authors find the opposite is true in CuTe and study the phenomenon using advanced q-EELS.

Introduction

Topological semimetals, standing for the three-dimensional analogues of two-dimensional graphene, feature symmetry-protected crossing of linearly-dispersing bands in the bulk electronic structures¹. Near the Fermi level, the nodal crossing of conical linearly-dispersing spectrum of $\hslash v_{\mathrm{F}}\mathbf{q}$ ($\hslash$, reduced Planck’s constant) conveys relativistic fermions, with $v_{\mathrm{F}}$ being the effective speed of light², and engenders topological phenomena free from classical counterparts^1,3. The iconic band crossing designates a finite density of states and the small number of relativistic fermions suggests a limited capacity in electronic screening¹, rendering the matters susceptible to electronic ordering, dubbed correlated topological quantum matters, with CDWs being an ubiquitous order^4–8.

In the cornerstone Peierls theory of CDWs, the order is prone to systems with the sheet-like Fermi surface (FS) and entangled with the divergence in electronic susceptibility, which is most prominent to bands decorated by linearly-dispersing $\hslash v_{\mathrm{F}}\mathbf{q}$ near the Fermi level^9,10. The linear dispersion links to that of topological semimetals, albeit the missing band crossing. The sheet-like FS facilitates nesting with q_CDW = 2k_F (q_CDW, CDW wave vector; k_F, Fermi wave vector), of which the long-range Coulomb interaction drives a sinusoidal modulation of $\cos 2{\mathbf{k}}_{\mathbf{F}}r$ (r, atomic coordinate) in the charge density and atomic positions^9–11. The corresponding lattice modulation depicts the condensed soft phonon mode and the overall energy gain is delineated by the opening of a gap ($\mathrm{\Delta }$), which represents the CDW order parameter^9–11.

Indeed, the CDW gapping accounts for the characteristic rise in resistivity across T_CDW⁹ and denotes certain electronic correlations that are customarily entangled with enhanced m* and reduced $v_{\mathrm{F}}$ of the carriers^4,12,13. A close inspection on this latter aspect reveals its conceptual relevance to doped Mott insulators^12,13, where the emergence of CDWs falls in a strong-coupling regime with the on-site Coulomb repulsion being larger than the kinetic energy of the electron liquid (scaled by the Fermi energy, E_F)^12,14,15. The charges therein are readily localized, massive and the concomitantly reduced $v_{\mathrm{F}}$ and enhanced m* are expected^12–15. In contrast, the Peierls context designates a weak-coupling CDW with $\mathrm{\Delta }<<{\mathrm{E}}_{\mathrm{F}}$ and weak charge localizations^9,15. The impact of the Peierls weak-coupling CDW on the m* and $v_{\mathrm{F}}$ is nonetheless short of comprehensive understanding, while can be arresting and sheds light on CDW-gapped correlated topological quantum matters at variance with Mott insulators^4–8,13.

Here, we report on the reduced m* and enhanced $v_{\mathrm{F}}$ below T_CDW of the model CDW material of semimetal CuTe, which harbors practically linearly-dispersing bands across the Fermi level and fulfills the Peierls ingredients of FS nesting and phonon condensation^16–23. The weak-coupling nature of $\mathrm{\Delta }<<{\mathrm{E}}_{\mathrm{F}}$ and weak charge localizations is established in this work. Moreover, CuTe is topologically trivial by the avoided linear-band crossing^16–19, which lifts suspicious topological CDWs^4,24 and refers to finite m* of the pertinent carriers instead of massless fermions tied to the crossed nodal feature^4,13. Typically, the measurement of m* ($v_{\mathrm{F}}$) is conducted by quantum oscillatory magnetoresistances⁴ (Landau-level spectroscopy¹³). Using q-EELS (inelastic electron scattering scheme, Supplementary Fig. 1 and supplementary information A), we demonstrate the simultaneous capturing of m* and $v_{\mathrm{F}}$ of the CDW-related electrons that emerge from the practically linearly-dispersing bands by temperature-dependent dispersions of the corresponding plasmon, which is the quanta of dynamical oscillations of the charges and a function of the m*, carrier density (n), and $v_{\mathrm{F}}$^25,26. Across T_CDW (335 K), we find that the marginal increase in m* of the CDW-related electrons from 0.27 m₀ (335 K) to 0.28 m₀ (300 K) is overwhelmed by the significant drop to 0.22 m₀ toward 100 K upon the growth in the CDW order at low temperatures. More specifically, the temperature-dependent m* below T_CDW follows the Bardeen-Cooper-Schrieffer (BCS) scaling of weak-coupling orders^9,15,27 and the concomitantly accelerated $v_{\mathrm{F}}$ from 1.61 (300 K) to 1.91 × 10⁸cm s⁻¹ (100 K) is close to 1.5 ~ 3 × 10⁸cm s⁻¹ of relativistic Dirac fermions in suspended graphene². The change in $v_{\mathrm{F}}$ across T_CDW (1.68 × 10⁸cm s⁻¹, 335 K) is otherwise small. Borrowing the established wisdom in the graphene², the m* reduction and $v_{\mathrm{F}}$ enhancement below T_CDW are discussed. Exploiting atomic-resolution EELS conjunct with scanning transmission electron microscopy (STEM; STEM-EELS), we also investigate the CDW potential and pertinent BCS-related electrostatic argument on the reduced m* and enhanced $v_{\mathrm{F}}$. Earlier q-EELS reports on the plasmon dispersions in CDW materials focus on the peculiar dispersions^28–35 that are also discussed hereby.

Results

The crystalline and electronic structures of CuTe

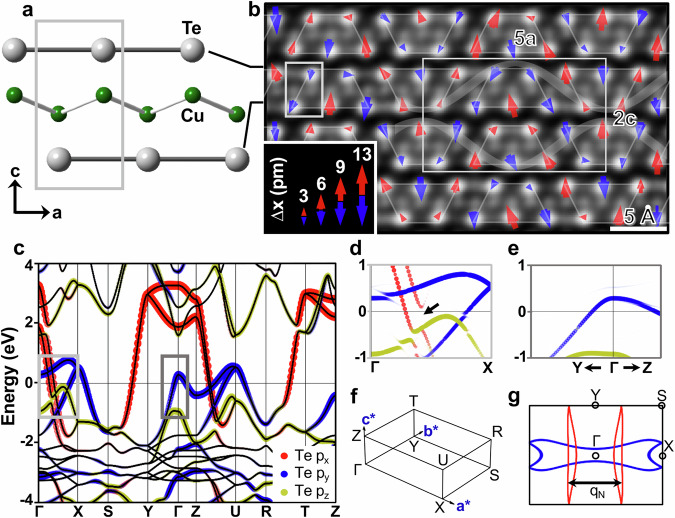
Figure 1a shows the unit cell of CuTe (Pmmn; a = 3.149, b = 4.086, and c = 6.946 Å) in the non-CDW, normal state, consisting of a-oriented Te chains and rumpling Cu nets in basal ab-plane¹⁶. Figure 1b exhibits the atomic-scale observation of the CDW at 300 K using STEM and reveals the dominant role of Te displacements ($\mathrm{\Delta }\mathrm{x}$, up- red and down-pointing blue arrows) in the characteristic 5a × 2c superlattice corresponding to the q_CDW = [0.4a*, 0, 0.5c*]^16,17,36,37. By grouping the red and blue arrows associated with the Te displacements into sets of trapezoids (Fig. 1b), two anti-phase coupled sinusoidal waves (gray) composed by the trapezoids depict the CDW order and suggest the condensed soft phonon mode³⁷. In Fig. 1b, an imperfection in the arrow-size repetition with the anticipated superperiodicity of 5a × 2c is noticed and arises from effects of noises unavoidably registered in the image due to finite sample drifts and mechanical vibrations upon experiments. Our picometer-level evaluations of the atomic displacements make these effects of small mechanical noises, which do not compromise the characteristic q_CDW = [0.4a*, 0, 0.5c*] of the image (Supplementary Fig. 2), directly visible³⁸.

Fig. 1. Lattices and electronic structures of the normal- and CDW-state CuTe.

a b-projected crystal structure in the normal state. Gray thick rectangle, unit cell. b STEM imaging of the CDW-modulated structure at 300 K. Gray thin rectangle, the CDW supercell of 5a × 2c with systematic Te displacements (∆x; picometer-level evaluations³⁸). The displacements organize into rows of trapezoids (gray) that show inverse Te-displacement directions in one trapezoid compared to the neighboring one in the same row, resulting in a wavelike displacement pattern of the periodicity of 5a. The Te displacements in the row right beneath (above) are anti-phase coupled, leading to the 2c periodicity. The gray sinusoidal waves, the wavelike, anti-phase coupled Te displacements. See text for the imperfection in the arrow-size repetition with the anticipated superperiodicity of 5a × 2c. c Electronic structure of the normal-state CuTe. Color, orbital decomposed Te-p states (black solid curves underneath, portraying the band dispersions). Black solid curves without color overlays, Cu 3d states. Fermi level, 0 eV. d Blowup of the CDW-state electronic structure along ΓX (i.e., the CDW counterpart to the light gray box in c). The CDW-gap opening at the Fermi level (black arrow) is dominated by one of the two practically linearly-dispersing Te-p_x bands. e Blowup of the CDW-state electronic structure around the dark gray-boxed region in c. f The high-symmetry directions in reciprocal space. g FS projected onto the X-Γ-Y plane at c* = 0. The Te-p_x bands (red) are sheet-like and in favor of FS nesting by q_N. The Te-p_y band (blue) forms a hole pocket.

In Fig. 1c, we show the element-, orbital-decomposed band diagram, not thus presented before^16,17,19,22, of the normal-state CuTe. Blowups of the CDW-state counterpart along ΓX and ΓY are displayed in Figs. 1d and e, respectively. Figure 1f denotes the high-symmetry points and Fig. 1g manifests the FS of the normal-state CuTe. Additional applications of exchange-correlation functionals, local field effects, and on-site Coulomb repulsions have negligible influences on these electronic structures¹⁹, unveiling the weak-correlation characteristic of CuTe.

Notably, the electronic characteristics of CuTe are predominated by the practically linearly-dispersing Te-p_x bands (red, Fig. 1c), which point to weak correlations and carriers with small m*^4,13,19, and parabolic Te-p_y bands (blue) near the Fermi level. Indeed, the Te-p_x (-p_y) bands has been suggested to carry an electron (hole) character with a light (heavy) band masss¹⁹. At the Fermi level, the CDW gaps out one of the Te-p_x bands (arrow, Fig. 1d), whereas the Te-p_y state remains intact (Figs. 1d and e). The nesting vector, q_N ~ 0.8 Å⁻¹, facilitated by the Te-p_x sheets on the FS (red, Fig. 1g) matches the projected a* vector of q_CDW (q_a = 0.4a* ~ 0.8 Å⁻¹)¹⁶. Unambiguously, the Te-p_x light electrons are pivotal to the CDW¹⁹ and we elaborate on m* and $v_{\mathrm{F}}$ of the carriers along the relevant ΓX direction. The Te-p_y heavy holes along ΓY are also tackled.

Capturing m* and ${\mathit{v}}_{\mathbf{F}}$ of the Te-p_x light electrons and Te-p_y heavy holes

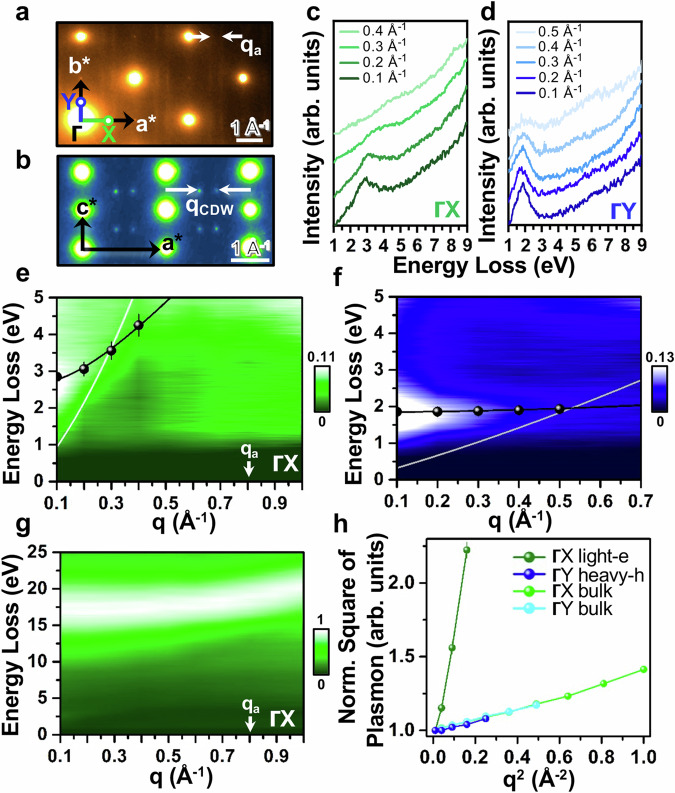
Figure 2a shows the ΓX-ΓY plane of the CDW state acquired by selected-area electron diffraction (SAED) at 300 K, with the zone-boundary X of ~1.0 Å⁻¹, Y of ~0.77 Å⁻¹, and the CDW q_a. The electron Ewald sphere intercepts q_CDW, which sits at the c*/2 plane neighboring to this plane, and results in the weak and streaky q_a’s in Fig. 2a. A direct observation of q_CDW in the a*c*-plane (Fig. 2b) is otherwise sharp.

Fig. 2. q-EELS investigations of plasmon dispersions in the CDW state at 300 K.

a The first ΓX and ΓY Brillouin zones by SAED. q_a, the projected a*-component of q_CDW onto this basal plane. b SAED pattern of the a*c* plane with the direct observation of q_CDW. c and d q-EELS measurements of the dispersions of respective Te-p_x light-electron and Te-p_y heavy-hole plasmons along ΓX and ΓY. e and f The respective plasmon-dispersion maps corresponding to c and d and further incorporating spectra up to the zone boundaries. g The bulk-plasmon dispersion map along ΓX. All spectra in c–g, ZLP removed. Black dots in e–f, pseudo-Voigt-fitted plasmon peak positions (error bars and also those in (h), standard errors in the fitting). Black curves in e–f calculated dispersions using Eq. (1). White curves in e–f the respective single-particle continua. h The ${\mathrm{\omega }}^2-{\mathrm{q}}^2$ scaling of the dispersions of ΓX light-electron, ΓY heavy-hole, ΓX bulk, and ΓY bulk plasmons in respective e–g and Supplementary Fig. 6a. Normalizations to the respective excitations at q² = 0.01 Å⁻² facilitate a direct comparison across different plasmons.

EELS probes electronic excitations and the loss function, $\mathrm{Im}\left\{\frac{-1}{\mathrm{\epsilon }\left(\mathrm{\omega },\mathbf{q}\right)}\right\}$ with $\mathrm{\epsilon }\left(\mathrm{\omega },\mathbf{q}\right)$ being the frequency($\mathrm{\omega }$)- and q-dependent complex dielectric function, diverges upon$\mathrm{\epsilon }\left(\mathrm{\omega },\mathbf{q}\right)$ = 0 that depicts the onset of a collective plasmon excitation (${\mathrm{\omega }}_{\mathrm{p}}$)^25,26. Fundamentally, the plasmon excitation in bulks reads as ${\mathrm{\omega }}_{\mathrm{p}}=\sqrt{\frac{4\mathrm{\pi }\mathrm{n}{\mathrm{e}}^2}{{\mathrm{m}}^{*}{\mathrm{\epsilon }}_{\infty }}}$, where e is the electron charge and ${\mathrm{\epsilon }}_{\infty }$ is the screening dielectric constant by the presence of single-particle transitions above the plasmon^25,26. The experimental observation of ${\mathrm{\omega }}_{\mathrm{p}}$ can resolve m* provided the temperature-dependent parameters of n and ${\mathrm{\epsilon }}_{\infty }$ are known^25,26,29,39.

Using q-EELS at 300 K, we observe the Te-p_x light-electron plasmon at 2.85 eV along ΓX at q = 0.1 Å⁻¹ (Fig. 2c and e; zero-loss peak, ZLP, removed) and the Te-p_y heavy-hole plasmon at 1.86 eV along ΓY (Fig. 2d and f; ZLP removed). A recent theoretical work suggests the Te-p_x light-electron (Te-p_y heavy-hole) plasmon at ~2.9 eV (~1.9 eV) around q = 0.1 Å⁻¹, which is now established and associated with the intraband transition of the Te-p_x (Te-p_y) states (Supplementary Fig. 3)¹⁹. At the Γ point (q = 0 Å⁻¹), the intense quasi-elastic tail due to the dynamical nature of electron scattering and also the finite momentum resolution of our apparatus (~0.09 Å⁻¹) buries these plasmons^35,40,41 (Supplementary Fig. 4) that are essentially an order of magnitude weaker than the bulk valence plasmon dispersing from ~17 eV (ΓX in Fig. 2g, ZLP-removed; Supplementary Figs. 5 and 6a). Upon the off-q setup (such as q = 0.1 Å⁻¹ hereby; meanwhile, having preserved the same momentum resolution) that effectively breaks the dynamical-scattering condition⁴¹, the intense tails can be significantly diminished and the light-electron and heavy-hole plasmons become resolvable (Fig. 2c and d).

For resolving m* of the Te-p_x light electrons, we firstly tackle ${\mathrm{\epsilon }}_{\infty }$ of the light-electron plasmon in the respective CDW and normal states using Drude-Lorentz (DL) modeling of the theoretical dielectric functions⁴², as shown in Supplementary Fig. 6b (inset). The readily DL-derived loss functions are also examined and the consistency with the theoretical ones and representative EELS exemplifications at CDW- 300 and normal-state 335 K (Supplementary Fig. 6b) indicates the satisfactory DL modeling, which suggests ${\mathrm{\epsilon }}_{\infty }$ ~ 1.41 and 1.59 for the respective CDW and normal phases at 300 and 335 K (supplementary information C). Subsequent derivations of the temperature-dependent ${\mathrm{\epsilon }}_{\infty }$ in respective CDW and normal states are shown in Supplementary Fig. 6c. Further attempts to n of the light electrons by Hall measurements (Supplementary Fig. 7) are, however, unsuccessful, because the significant hole contribution masks the light electrons²¹. In effect, the q-dependent plasmon dispersion provides the direct access to $v_{\mathrm{F}}$, m*, and n, although largely unnoticed in the q-EELS literature^{28–35,40,43–45}. The methodology is demonstrated below.

In a bulk material with dense n, the kinetic energy of electrons (E_F ~ n^2/3) overwhelms the inter-particle potential energy and the charges behave like a free electron gas (FEG)²⁶. The random-phase approximation (RPA) in this FEG context depicts the plasmon dispersion, which scales with $v_{\mathrm{F}}$, by Eq. (1)^25,26.

$${\mathrm{\omega }}^2={\mathrm{\omega }}_{\mathrm{p}}^2+\frac{3}{5}{v}_{\mathrm{F}}^2{\mathbf{q}}^2$$ 1

Fundamentally, Eq. (1) is derived for classical, massive electron systems with the characteristic parabolic band-dispersion of $\mathrm{E}=\frac{{\hslash }^2{\mathbf{k}}^2}{2{\mathrm{m}}^{*}}$ (i.e., the Te-p_y bands in Fig. 1c−e)⁴⁶. For massless Dirac fermions harbored at the crossed nodal point of conical linearly-dispersing bands with $\hslash v_{\mathrm{F}}\mathbf{q}$^2,46,47, the corresponding long-wavelength ${\mathrm{\omega }}_{\mathrm{p}}$ at q = 0 Å⁻¹, like that in Eq. (1), turns out to be non-classical and proportional to $1/\sqrt{\hslash }$, whereas the plasmon dispersion still obeys the q² dependence as the plasmon in the classical counterpart⁴⁶. The avoided linear-band crossing in CuTe (Fig. 1c) profoundly lifts the plausibility of a massless character of the related Te-p_x electrons, the practically linear-band dispersion of which is, in effect, designated for characteristically small m*^4,13,19. Such Te-p_x light electrons with finite m*, as well as the Te-p_y heavy holes, would prompt for the application of Eq. (1) for the pertinent plasmon dispersions.

Notably, the slope (A) upon the ${\mathrm{\omega }}^2-{\mathrm{q}}^2$ scaling of Eq. (1) is a probe of $v_{\mathrm{F}}^2$ ~ A, and the simultaneously intercepted ${\mathrm{\omega }}_{\mathrm{p}}^2$ at q = 0 Å^-1 is a function of m* by ${\mathrm{m}}^{*}=\frac{4\mathrm{\pi }\mathrm{n}{\mathrm{e}}^2}{{\mathrm{\omega }}_{\mathrm{p}}^2{\mathrm{\epsilon }}_{\infty }}$. Considering $v_{\mathrm{F}}=\frac{\hslash {\left(3{\mathrm{\pi }}^2\mathrm{n}\right)}^{1/3}}{{\mathrm{m}}^{*}}$ in bulks, the elaborated A ~ $v_{\mathrm{F}}^2$ yields $\mathrm{n}~\frac{{\mathrm{\omega }}_{\mathrm{p}}^3\cdot {\mathrm{\epsilon }}_{\infty }^{3/2}}{A^{3/4}}$. With the resolved n, m* becomes directly accessible and $v_{\mathrm{F}}$ is calculated.

In Fig. 2h, we show the ${\mathrm{\omega }}^2-{\mathrm{q}}^2$ scaling of the dispersions of ΓX light-electron, ΓY heavy-hole, ΓX bulk, and ΓY bulk plasmons in respective Fig. 2e–g and Supplementary Fig. 6a, with the linearity in A ~ $v_{\mathrm{F}}^2$ by Eq. (1) suggesting a FEG character (supplementary information D) despite the CDW order. This FEG essence reconciles the ignorable correlation effects in Fig. 1c–e and g.

Using the experimental A of the light-electron plasmon (Fig. 2h), we then obtain n = 2.01 × 10²¹cm⁻³ of the Te-p_x light electrons. The concomitantly intercepted ${\mathrm{\omega }}_{\mathrm{p}}$ of 2.65 eV at q = 0 Å⁻¹ resolves m* = 0.28 m₀. With the m* and n, $v_{\mathrm{F}}$ = 1.61 × 10⁸cm s⁻¹ and E_F ~ 2.07 eV are derived as summarized in Table 1, along with those of the Te-p_y heavy holes that also adopt ${\mathrm{\epsilon }}_{\infty }$ ~ 1.41 due to the likewise appearance of interband transitions above the plasmon (Supplementary Fig. 5d). The valence electrons for isotropic ΓX and ΓY bulk-plasmon dispersions (Fig. 2h) are otherwise of m* = 1.12 m₀ and n = 2.37 × 10²³cm⁻³ in average (supplementary information D).

Table 1.

The physical parameters of Te-p_x light electrons and Te-p_y heavy holes derived from the respective plasmon dispersions at 300 K

Physical Parameters	Te-px light electrons	Te-py heavy holes
Effective mass m* (m0)I	0.28	3.41
Carrier density n (cm−3)	2.01 × 1021	1.19 × 1022
Carrier density n, Hall (cm−3)II	7.34 × 1021 (//a)	1.16 × 1022 (//b)
Fermi velocity $v_{\mathrm{F}}$ (cm s−1)	1.61 × 108	0.24 × 108
Fermi wave vector kF (Å−1)	0.39	0.71
Critical wave vector qc (Å−1)	0.3	1.39
Fermi Energy EF (eV)	2.07	0.56

^I The intercepted ${\mathrm{\omega }}_{\mathrm{p}}$ at q → 0 Å^-1 of the heavy-hole plasmon is 1.85 eV.

^II Results by Hall measurements (Supplementary Fig. 7), in which the positive signs of Hall coefficients along both a- and b-axes indicating predominant hole contributions in transports.

Using the $v_{\mathrm{F}}$ in Table 1, we calculate the dispersions of Te-p_x light-electron (black curve, Fig. 2e) and Te-p_y heavy-hole plasmons (black curve, Fig. 2f) by Eq. (1), and find a remarkable consistency with the experiments (black dots, pseudo-Voigt fitted peak positions; Supplementary Figs. 8a-b with ZLP-removed spectra). The respective single-particle continua, $\frac{{\hslash }^2\left({\mathbf{q}}^2+2\mathbf{q}{\mathbf{q}}_{\mathbf{c}}\right)}{2{\mathrm{m}}^{*}}$ with the critical wave vector q_c of $\frac{{\mathrm{\omega }}_{\mathrm{p}}}{v_{\mathrm{F}}}$, are also derived (white curves, Fig. 2e–f)^25,26. Beyond the single-particle crossovers at 0.29 Å⁻¹ (Fig. 2e) and 0.52 Å⁻¹ (Fig. 2f), the respective light-electron and heavy-hole plasmons are to be subject to Landau damping and decay into electron-hole pairs^25,26,29. Indeed, we observe appreciably damped, broadened, and weakened light-electron plasmon at q > 0.3 Å⁻¹ (Fig. 2c; Supplementary Figs. 8 and 9) and also decaying heavy-hole plasmon at q = 0.5 Å⁻¹ (Fig. 2d; Supplementary Figs. 8 and 9). The derived k_F ~ 0.39 Å⁻¹ of the Te-p_x light electrons corresponds to 2k_F = q_N ~ 0.78 Å⁻¹, matching q_N ~ 0.8 Å⁻¹ in Fig. 1g¹⁶. All these fundamental agreements highlight the robustness in our plasmon-dispersion methodology for m* and $v_{\mathrm{F}}$.

Reduced m* and enhanced ${\mathit{v}}_{\mathbf{F}}$ of the light electrons below T_CDW and the BCS weak-coupling CDW

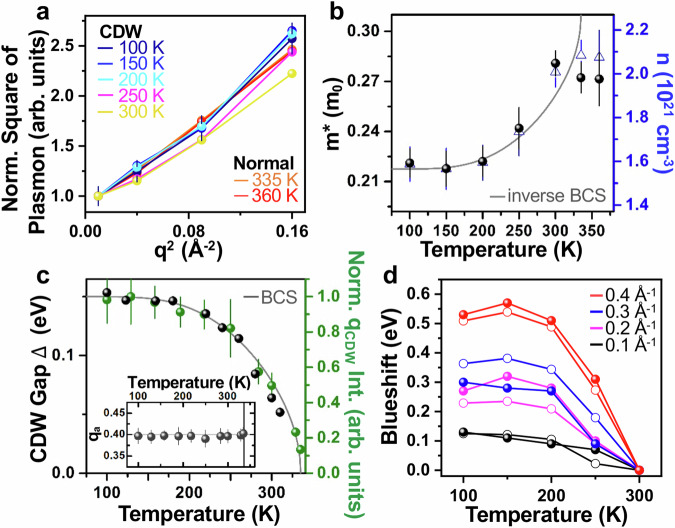
Figure 3 shows the temperature-dependent plasmon dispersions (all spectra, ZLP-removed). Below T_CDW, the Te-p_x light-electron plasmon at q = 0.1 ~ 0.3 Å⁻¹ manifests a blueshift with decreasing temperatures (Fig. 3a–c). At q = 0.4 Å⁻¹ (Fig. 3d), the onset of Landau damping damps the plasmons into broad, weak excitations, whereas they are still well discernible from the spectral backgrounds and enable the associated plasmon-peak fittings (Supplementary Fig. 8c). The readily fitted plasmon-peak positions (inverse black triangles, Fig. 3d) also unveil a blueshift below T_CDW. In contrast, the Te-p_y heavy-hole plasmon is robust against temperatures (Fig. 3e–h) and we have known from Fig. 1d–e that the Te-p_y heavy holes are irrelevant with the CDW. The Te-p_x light electrons dictate the CDW order and such a plasmon blueshift in CDWs has not been thoroughly understood³⁹.

Fig. 3. Plasmon dispersions across the CDW transition at 335 K.

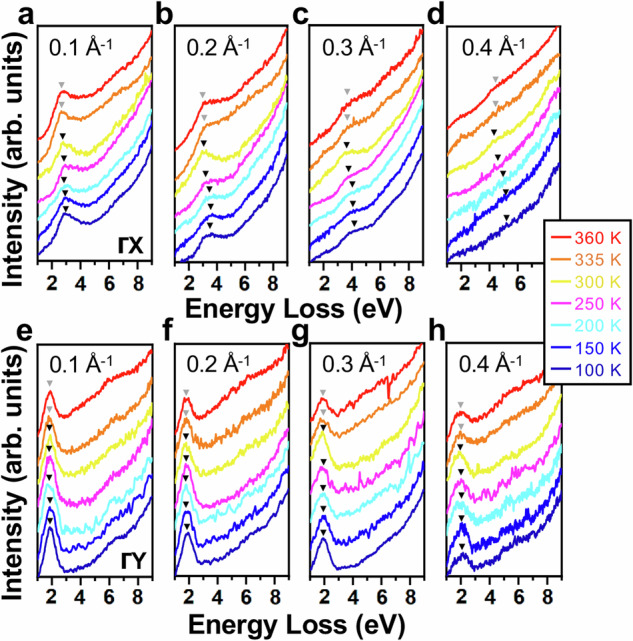
a–d q-EELS spectra of the Te-p_x light-electron plasmons at 0.1, 0.2, 0.3, and 0.4 Å^-1 along ΓX as a function of temperatures (100 ~ 360 K). e–h The Te-p_y heavy-hole counterparts along ΓY. All spectra, ZLP removed. Black and gray inverse triangles, pseudo-Voigt-fitted plasmon peak positions (error bars, neglected for clarity of the presentation) in respective CDW and normal states.

Figure 4a exhibits the ${\mathrm{\omega }}^2-{\mathrm{q}}^2$ scaling of the light-electron plasmon dispersions across T_CDW in Fig. 3a–d. Figure 4b shows the readily resolved m* and n and, more noticeably, their remarkable agreements with a BCS-related temperature dependence of the weak-coupling order below T_CDW^9,27, regardless of a marginally small increase in m* across T_CDW (0.28 m₀, 300 K; 0.27 m₀, 335 K). Figure 4c indicates, below T_CDW, both the CDW order-parameter $\mathrm{\Delta }$³⁷ and q_CDW intensity at [0.4a*, 1b*, 0.5c*] evolve in accordance with the BCS scaling (Fig. 4c) and the weak-coupling CDW essence of $\mathrm{\Delta }<<{\mathrm{E}}_{\mathrm{F}}$ ~ 2.07 eV (Table 1) is satisfied^9,15,27. The CDW is firmly a weak-coupling Peierls instability within the BCS context^9,15 and impacts the plasmon dispersions (Fig. 3a–d) by decreasing m* and n below T_CDW at the growth of the CDW order-parameter strength (Fig. 4c), at odds with the notion of enhanced m* and reduced $v_{\mathrm{F}}$ upon increasing electronic correlations^12–14.

Fig. 4. Deriving m* and n of the CDW-related Te-p_x light electrons and the BCS context of the weak-coupling CDW.

a The ${\mathrm{\omega }}^2-{\mathrm{q}}^2$ scaling of the dispersions of Te-p_x light-electron plasmons in Fig. 3a-d. Normalizations to the respective excitations at q² = 0.01 Å⁻² facilitate a direct comparison across different temperatures. Error bars, standard errors in the fitted plasmon peaks and only shown for 100 K’s for clarity of the presentation. b The resolved m* and n of the light electrons from the linearly-fitted slopes in a. Gray curve, the inverse BCS-temperature dependence. Error bars, standard errors upon the linear fitting. c Evolutions of the CDW-gap size $\mathrm{\Delta }$ (reproduced from Ref. ³⁷) and q_CDW-superlattice intensity (normalized to the neighboring Bragg spot) across T_CDW. Inset, the robust commensurability of the CDW superlattice down to 100 K. Gray curve, the BCS-temperature dependence. Error bars in the normalized q_CDW-superlattice intensity (green) and commensurability (inset), standard deviations upon the averaging over five diffraction patterns. d The temperature-dependent plasmon blueshifts at each q with reference to the excitations at 300 K. Solid dots, experimental results derived from Fig. 3a–d. Open dots, theoretical counterparts using Eq. (1).

Figure 4d exhibits the q-, temperature-dependent plasmon blueshifts (solid dots), which are derived from Fig. 3a–d with reference to the 300-K excitations at various q’s, and the theoretical counterparts (open dots) are calculated by Eq. (1) using the enhanced $v_{\mathrm{F}}$ below T_CDW toward 100 K in Fig. 5a. The consistency in the experimental, theoretical results (Fig. 4d) confirms the central finding of our work, below T_CDW the weak-coupling CDW reducing m* and enhancing $v_{\mathrm{F}}$ of the Te-p_x light electrons by ~20%.

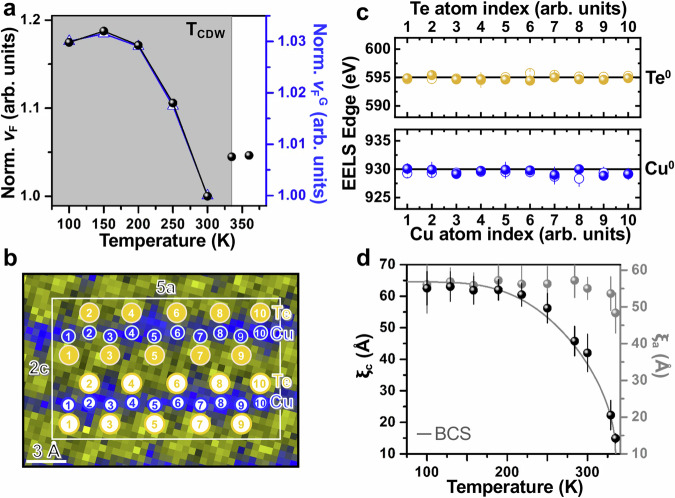
Fig. 5. v_F of the light electrons, STEM-EELS of the CDW at 300 K, and CDW coherence lengths.

a The calculated $v_{\mathrm{F}}$ of the Te-p_x light electrons. Black ($v_{\mathrm{F}}$), calculated results using the temperature-dependent m* and n in Fig. 4b. Blue ($v_{\mathrm{F}}^{\mathrm{G}}$), calculations using Eq. (2) formulated for graphene. For clarity, all results normalized to the respective ones at 300 K. b, STEM-EELS elemental mapping of the CDW superlattice. Blue (yellow), Cu (Te). Solid (open) blue symbols, crystallographic Cu sites in the upper (lower) c portion of the 5a × 2c supercell. Solid (open) yellow symbols, Te in the upper (lower) part of the superlattice. c STEM-EELS probing of the Cu and Te core-level edges at each crystallographic site in (b) (related STEM-EELS spectra, Supplementary Fig. 12). Error bars, standard errors upon the analyses of the first derivative of the STEM-EELS spectra. Black horizontal lines, excitation edges of metallic Cu⁰ and Te⁰ acquired on thin metal-foil references. d The temperature-dependent coherence lengths of the CDW along c- (ξ_c, black) and a-axes (ξ_a, gray), respectively. Gray curve, the temperature dependence in accordance with the BCS theory. Error bars, standard deviations upon the averaging over five diffraction patterns.

The weak, frozen CDW potential below T_CDW and the linear-band renormalization in graphene

The light m* of the CDW-related Te-p_x electrons (0.22 ~ 0.28 m₀, Fig. 4b) below T_CDW points out a weak correlation of the order²³, which is anticipated for the weak electronic correlation inherent to linearly-dispersing bands¹³ and echoes the weak-coupling essence in Fig. 4c, and is to feature a weak charge localization¹⁴. Using STEM-EELS, we address this charge problem. The STEM-EELS elemental mapping of the CDW at 300 K is shown in Fig. 5b and the core-level edges, indicative of charge-valence states^38,48–50 (corresponding spectra, Supplementary Fig. 12), of the constituent atoms are exhibited in Fig. 5c. All the Te and Cu atoms (Fig. 5c and Supplementary Fig. 12) display their respective edges around those of metallic Te⁰ and Cu⁰. By our STEM-EELS detection limit of 0.03 e per unit cell^48–50, the atom-by-atom charge variation across the CDW superlattice would then be within Te^± 0.03 and Cu ^± 0.03, appreciably smaller than the order of ± 0.1 in localized, correlated charge orders^14,48. The approximate electrostatic potential of the weak-coupling CDW would correspond to 0.02 eV at maximum (supplementary information E)⁵⁰. With decreasing temperatures, Fig. 5d further addresses the coherence lengths of the CDW along a- (ξ_a) and c-axes (ξ_c), evaluated by the respective inverse breadths of q_CDW at [0.4a*, 1b*, 0.5c*] along a* and c*. Below T_CDW, ξ_a is robustly of ~55 Å (~3.5 × 5a, Fig. 5c), whereas ξ_c scales with the BCS dependence (~14 Å ≈ 2c, 300 K; ~62 Å ≈ ~ 4.5 × 2c, 100 K). The weak-coupling CDW is, in effect, fluctuating along c-axis near T_CDW and frozen into a growingly spatially coherent order at reduced temperatures (supplementary information E). Accordingly, the CDW potential becomes more coherent toward 100 K and yields a smoother electrostatic background that may reduce electron scattering and could possibly be in favor of the reduced m* (Fig. 4b) and enhanced $v_{\mathrm{F}}$ (Fig. 5a) below T_CDW³⁹. However, this electrostatic argument for the m* and $v_{\mathrm{F}}$ features shall not be the most essential underlining factor, since the absence of a CDW potential above T_CDW does not facilitate even lighter m* (Fig. 4b) and faster $v_{\mathrm{F}}$ (Fig. 5a) than those of the electrons at low temperatures.

We, therefore, seek for otherwise hints from band perspectives. Indeed, the reduced n (Fig. 4b) by CDW gapping of the practically linearly-dispersing Te-p_x band reminds us of the canonically reduced m* and enhanced $v_{\mathrm{F}}$ by decreasing n in gated suspended graphene². The free-standing geometry lifts dielectric screening by a substrate and the graphene is subject to sole inherent electronic screening, for which the lower the gating-tunable n, the weaker the screening^2,51. The weak screening turns on increased electron-electron interactions², which renormalize the conical $\hslash v_{\mathrm{F}}\mathbf{q}$ spectrum near the Fermi level by amplified $v_{\mathrm{F}}$ and reduced m*. Equation (2) denotes the characteristic logarithmical dependence of the $v_{\mathrm{F}}$ on n and is borrowed for the Te-p_x light electrons in the CDW state with $v_{\mathrm{F}}$ = 1.61 × 10⁸cm s⁻¹ (300 K, Table 1) that is distinctly compatible with $v_{\mathrm{F}}$ of the graphene (1.5 → 3 × 10⁸cm s⁻¹ upon decreasing n₀ → n; m* ~ 10^-2 → 10^-3 m₀, concomitantly)².

$$v_{\mathrm{F}}\left(\mathrm{n}\right)=v_{\mathrm{F}}\left({\mathrm{n}}_0\right)\left[1+\frac{{\mathrm{e}}^2}{8{\mathrm{\epsilon }}_{\mathrm{G}}\hslash v_{\mathrm{F}}\left({\mathrm{n}}_0\right)}\ln \left(\frac{{\mathrm{n}}_0}{\mathrm{n}}\right)\right]$$ 2

where the n₀ and $v_{\mathrm{F}}\left({\mathrm{n}}_0\right)$ are mimicked by the respective n and $v_{\mathrm{F}}$ of CuTe at 300 K, the decreasing gating-tunable n is regarded as the temperature-dependent n in Fig. 4b, and the effective screening constant ${\mathrm{\epsilon }}_{\mathrm{G}}$ of graphene is replaced by the temperature-dependent ${\mathrm{\epsilon }}_{\infty }$ in Supplementary Fig. 6c. Figure 5a shows the thus-elaborated graphene analogy of $v_{\mathrm{F}}^{\mathrm{G}}$ (blue) superimposed with the experimentally derived $v_{\mathrm{F}}$ (black). Remarkably, the normalized temperature dependences of respective $v_{\mathrm{F}}$ and $v_{\mathrm{F}}^{\mathrm{G}}$ below T_CDW are almost identical (Fig. 5a), albeit the difference in magnitudes of the $v_{\mathrm{F}}$ and $v_{\mathrm{F}}^{\mathrm{G}}$ due to the small coupling term, $\frac{{\mathrm{e}}^2}{\hslash v_{\mathrm{F}}\left({\mathrm{n}}_0\right)}$, of graphene². Indeed, the Peierls instability is dictated by Coulomb interactions and the growth in the CDW order-parameter strength below T_CDW (Fig. 4c) delineates increasing electronic interactions upon the decreasing n (Fig. 4b)^9,51, reconciling the elevated electron-electron interaction for reduced m* and enhanced $v_{\mathrm{F}}$ in the graphene². A linear-band renormalization like that in the graphene² could be at work in the CDW-state CuTe concerning the practically linearly-dispersing Te-p_x bands, and might delineate the lighter m* (Fig. 4b) and faster $v_{\mathrm{F}}$ (Fig. 5a) below T_CDW.

The q-EELS stands out as an emergent tool for simultaneous tackling of m* and $v_{\mathrm{F}}$. Although the increased resistivity by CDW gapping would hinder quantum oscillatory measurements of m*^4,23, we are aware that the exceptionally low resistivity of CDW-gapped CuTe has facilitated quantum oscillations (down to 2 K and up to 14 T) and resulted in m* of ~0.13, ~0.23, and ~0.35 m₀, of which the respective electronic origins are unspecified²³. Meanwhile, the limited accessibility to lower temperatures and higher magnetic fields renders heavier carriers in CuTe invisible²³. Our q-EELS, capable of unraveling the Te-p_y heavy holes (Table 1), resolves m* ~ 0.22 m₀ of the Te-p_x light electrons at the BCS low-temperature limit (Fig. 4b). The consistency with the reported m* ~ 0.23 m₀ at 2 K²³ insinuates that the heavier ~0.35-m₀ electrons thereby may represent survived carriers from high temperatures (~0.28-m₀, our work), and their numbers could be so small that they are below our EELS detection limit^48,49, thus unobservable in Fig. 3a–d. The reported light ~0.13-m₀ electrons are not found in our q-EELS, while they are anyhow inconsistent with the band diagram²³.

Indeed, there have been continuous interests in plasmon dispersions in CDW systems and q-EELS with its accessibility to a broad q range renders this technique unparalleled for the subject^28–35. The q-EELS study below the T_CDW in 1T-TiSe₂ has reported the softening and condensation of the plasmon at the characteristic modulation wave vector²⁸, which represents a phenomenon absent in CuTe with quadratic dispersions (Figs. 2c–e, and 3a–d) and damped, vanishing excitations toward q_a (Fig. 2e). The more recent q-EELS investigation on 1T-TiSe₂ unambiguously indicates that the designated plasmon in Ref. ²⁸ is, in effect, an inherent phonon mode and the plasmon locates at a slightly higher energy, close to the opening CDW-gap size below the T_CDW and thus dramatically attenuated by the gapping²⁹. In the 2H class of transition-metal-dichalcogenide 2H-NbSe₂ and 2H-TaSe₂, a likewise negative dispersion of the plasmon has been observed and attributed to the electronic impact of the CDW order below the T_CDW^30,31. The negative dispersion is, however, proven to be irrelevant with the CDW instability and merely a band-structure effect that delineates the persistence of an interband transition above the plasmon and screening the collective excitation down to a lower energy^32,33. The plasmons in the CDW materials of (TaSe₄)₂I and K_0.3MoO₃ have also been studied, whereas the q-EELS experiments were conducted above the T_CDW and the respective correlations of the plasmons with the CDW orders remain unresolved^34,35. There are rising interests in q-EELS probing of the quanta of the collective magnetic excitations of magnons and state-of-the-art EELS with meV resolution is indispensable considering the typical excitations of few tens of meV similar to those of phonons^52–54. The q-EELS probing of magnon dispersions is complementary to the conventional tackling by inelastic neutron scattering with low scattering cross sections and deserves future devotions⁵⁴.

Discussion

The Peierls instability of CuTe fulfills both the classical BCS notion on weak-coupling CDWs and the quantum ingredient of gapped, practically linearly-dispersing $\hslash v_{\mathrm{F}}\mathbf{q}$ bands. The growing CDW order below T_CDW reduces m* and enhances $v_{\mathrm{F}}$ of the pertinent light electrons, in stark contrast to enhanced m* and reduced $v_{\mathrm{F}}$ upon correlated electronic orders. The analogy to the reduced m* and enhanced $v_{\mathrm{F}}$ of the band-renormalized graphene (Fig. 5a) sheds essential light on our explorations, which have far-reaching implications on the timely open question of m* and $v_{\mathrm{F}}$ of relativistic fermions in a wide spectrum of CDW-gapped topological Dirac and Weyl semimetals with emergent quantum phenomena^4–7,13. Moreover, a pressurized superconducting cuprate has been shown to manifest reduced m*⁵⁵ and the superconductivity found in pressurized CuTe may be associated with our observed reduced m* of the light electrons⁵⁶. Whether our discovery of the reduced m* and enhanced $v_{\mathrm{F}}$ below T_CDW is general to all Peierls CDWs of the weak-coupling BCS and $\hslash v_{\mathrm{F}}\mathbf{q}$-band dispersion essences prompts for extensive inspections.

Methods

The electron-microscopy specimen preparations

The basal ab-plane specimens for the q-EELS studies were prepared by mechanical exfoliations. The cross-sectional, b-projected specimens for STEM imaging and STEM-EELS were achieved by microtome thin-foil sectioning.

The q-EELS experimental setup for plasmon excitations

The inelastic electron scattering scheme of q-EELS can be found in Supplementary Fig. 1 and supplementary information A. The q-EELS and accompanied electron-diffraction experiments were conducted on FEI Tecnai G2 operated at 200 kV. A Gatan liquid-nitrogen specimen holder was exploited for our investigations at 100 ~ 360 K. Using a circular EELS-collection aperture of 2.5 mm in diameter and a diffraction-pattern projection length of 6.8 m, the momentum resolution attains ~0.09 Å⁻¹ and allows the sampling of the ΓX and ΓY directions with the optimized q step of 0.1 Å⁻¹. The q-EELS acquisition at q = 0 ~ 0.3 Å⁻¹ was achieved within 2 seconds and the concomitant energy resolution was of 0.54 eV. For q ≥ 0.4 Å^-1, the longer acquisition time of 6 ~ 8 seconds due to the weaker electronic excitations was required and marginally changes the energy resolution to 0.57 ~ 0.63 eV that does not noticeably affect the spectral line-shapes. Each q-EELS spectrum in this work represents the summation of nine individual spectra with high spectral reproducibility. Moreover, all q-EELS spectra shown are the results of the ZLP removal using the method of fitting pre-measured ZLP registered in the same experimental conditions at given q’s (Supplementary Fig. 4c and 4e).

The STEM-EELS experiments for core-level excitations

The STEM-EELS investigations were carried out at room temperature on JEOL 2100 F equipped with an aberration corrector and featuring the spatial (energy) resolution of ~0.9 Å (0.9 eV). The electron-probe convergence angle of 20 mrad and STEM-EELS collection angle of 30 mrad were exploited. The STEM-EELS datasets on CuTe and reference-Cu and -Te metal foils were firstly subject to the random-noise reduction by the principal-component analysis and then the power-law background removal prior to the respective Cu-L and Te-M edge retrievals^48–50. The STEM-EELS elemental mapping of Te and Cu was then accomplished by integrating the respective spectral intensities centered at the indicated vertical lines in Supplementary Fig. 12 (bottom panels) with the integral-window size of 2 eV. The spectra of the Te-1 and Cu-1 atoms (top panels, Supplementary Fig. 12) are the respective integrals of 2 × 2 pixels underneath (pixel size, ~0.4 Å) and those of all Te and Cu atoms are the integrals of all the associated atoms in the 5a × 2c supercell of the CDW. The reference Cu- and Te-foil spectra are the integrals over 30 × 30 pixels, respectively.

First-principles simulations

The ground-state electronic structures of CuTe were calculated using the first-principles package Quantum Espresso⁵⁷ with norm-conserving pseudopotential within the framework of density-functional theory (DFT). To achieve the converged wavefunctions, eigenvalues and optimized atomic configurations of the normal-state CuTe were considered and an energy cutoff of 120 Ry and the k-grids sampling of 40 × 32 × 16 for the respective expanding plane-wave basis set and approximate Brillouin zone integral were performed. Based on the density functional perturbation theory, the supercell geometry of the CDW was fully relaxed under the guidance of the eigenmode of the soft-phonon onset at q_CDW = [0.4a*, 0, 0.5c*]. The symmetry-breaking effect on the electronic band structure of the CDW was elucidated by band unfolding using unfold-x code⁵⁸. To simulate the q-EELS spectra of both the normal- and CDW-state CuTe without suffering from the dramatically time-consuming unoccupied state summations, we carried out a Liouville-Lanczos approach to the linear-response time-dependent DFT implemented in turboEELS⁵⁹. A considerable number of Lanczos iterations up to 9000 with the extrapolation to 60000 Lanczos coefficients was exploited for achieving converged EELS results at each q. The calculations on the transition-channel dependent dielectric functions (Supplementary Fig. 3) were accomplished through implementations in BerkeleyGW⁶⁰ within RPA based on the many-body perturbation theory.

Hall measurements

We cleaved the crystals and cut them into thin rectangular pieces with a typical dimension of ~1.7 × 0.6 × 0.06 mm³. Five indium leads were soldered and a Hall-measurement geometry was formed for simultaneous tackling of longitudinal (ρ_xx) and transverse (ρ_xy) resistivities using the standard DC four-probe technique. Hall voltages were measured by reversing the magnetic field direction at a fixed temperature to eliminate the offset voltage due to the asymmetric Hall terminals. The Hall coefficient measurements were acquired in a magnetic field parallel to c-axis up to 6 T, and a typical DC current density of ~50 A cm ^− 2 was applied to the crystal parallel to a- or b-axis.

Author contributions

I.T.W. conducted q-EELS experiments and T.L.C. carried out electron-diffraction and STEM-EELS studies. C.E.H. and H.C.H. performed first-principles calculations. Z.L. and L.M.W. undertook transport measurements. P.H.L. and C.W.L. contributed the CDW-gap data by ARPES. C.W.C. supervised the work. C.N.K. and C.S.L. grew the materials. C.H.C. and M.W.C. carried out all analytical theoretical calculations. M.W.C. wrote the manuscript. All the authors contributed to the discussion and interpretation of the results.

Peer review

Peer review information

Nature Communications thanks Xuetao Zhu, and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data that support the finding of this paper are presented in the main article and supplementary information.

Code availability

The first-principles ground-state calculations are performed by the Quantum ESPRESSO codes (https://www.quantum-espresso.org/). The EELS calculations up to high-energy regime are carried out using the turboEELS code (a component of Quantum ESPRESSO) and a further transition-channel analysis of the q-dependent dielectric function in a low-energy range is conducted by the BerkeleyGW code (https://berkeleygw.org/). The principal-component analysis for the random-noise reduction in STEM-EELS datasets is undertaken within the framework of the multivariate-statistical analysis by HREM Research (https://www.hremresearch.com/msa/).

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-53653-z.