Abstract
Next-generation data networks need to support Tb/s rates. In-phase and quadrature (IQ) modulation combine phase and intensity information to increase the density of encoded data, reduce overall power consumption by minimizing the number of channels, and increase noise tolerance. To reduce errors when decoding the received signal, intersymbol interference must be minimized. This is achieved with pure phase modulation, where the phase of the optical signal is controlled without changing its intensity. Phase modulators are characterized by the voltage required to achieve a π phase shift, Vπ, the device length, L, and their product, VπL. To reduce power consumption, IQ modulators are needed with <1 V drive voltages and compact (sub-cm) dimensions, which translate in VπL < 1Vcm. Si and LiNbO3 (LN) IQ modulators do not currently meet these requirements because VπL > 1Vcm. Here, we report a double single-layer graphene (SLG) Mach–Zehnder modulator (MZM) with pure phase modulation in the transparency regime, where optical losses are minimized and remain constant with increasing voltage. Our device has VπL ∼ 0.3Vcm, matching state-of-the-art SLG-based MZMs and plasmonic LN MZMs, but with pure phase modulation and low insertion loss (∼5 dB), essential for IQ modulation. Our VπL is ∼5 times lower than the lowest thin-film LN MZMs and ∼3 times lower than the lowest Si MZMs. This enables devices with complementary metal-oxide semiconductor compatible VπL (<1Vcm) and smaller footprint than LN or Si MZMs, improving circuit density and reducing power consumption by 1 order of magnitude.
Keywords: graphene, photonics, modulators, optoelectronics, layered materials.
The global Internet traffic was expected to triple between 2019 and 2024 with the advent of 5G and the Internet of everything.1 Lockdowns in response to COVID-19 shifted the distribution of data traffic across the network,2 with an additional ∼20–200% rise,3 due to remote working3,4 and increased use of home entertainment services.5 This vast amount of data relies on a backbone of high-density data network infrastructures, with 2018 standards of 400Gb/s6 to be extended >1Tb/s by 2025.7 To go >1Tb/s it is preferable to increase data rates in a single channel8,9 rather than the number of channels. By minimizing the number of channels, the power consumption and system complexity is reduced, because less electrical drivers and active optical components are needed.8,9 The bandwidth (BW) of a single channel that uses binary modulation formats is limited by that of the electrical interfaces used to drive the active optical components.8,9 These struggle to exceed 2023 standards7 because losses increase with increased frequencies.10 Consequently, for data rates >100Gb/s, binary modulation formats11 have been replaced by 4-level pulse-amplitude modulation (PAM).6 PAM uses 4 amplitude levels of the transmitted optical signal, to represent 4 symbols that correspond to 2 bits of information.8 Other multilevel modulation schemes, such as quadrature amplitude modulation (QAM),11 encode information in both phase and amplitude.11 Transmission systems that use only amplitude modulation (AM) are known as direct detection systems.11 Those that use both phase modulation (PM) and AM are known as coherent, because the phase difference between two or more signals remains constant over time.11 Coherent systems have a higher noise tolerance than direct detection ones, because the signal degradation from fiber dispersion can be compensated by the received signal phase.11
Information is transmitted by electro-optic (EO) modulators that convert an electrical signal into an optical one.12 This can be encoded into the intensity of the transmitted signal, known as AM, or electro-absorption modulation,12 and into the phase, known as PM or electro-refractive modulation.12 In-phase and quadrature (IQ) modulators are interferometric devices that use pure PM, with no change of amplitude, to generate the different QAM symbols.11 No direct AM is required to generate QAM symbols, because the interferometer converts a phase difference into a change in amplitude.11 To reduce intersymbol interference, therefore errors at the receiver,11 the symbol noise should be minimized, and symbols should be evenly spaced in the in-plane and quadrature axes.11 Thus, any unwanted AM will increase symbol noise, and any nonlinear PM will result in irregular symbol spacing.11
An important
parameter for comparing phase modulators is the product
of the voltage required to achieve a π phase shift, Vπ, and the device length, L.13 The additional optical loss resulting
from inserting the device in the transmission line is the insertion
loss IL = αL, where α is the absorption
coefficient per unit length.14 In order
to reduce overall power consumption, we need to minimize VπL and IL,14 because a lower VπL reduces the device area and capacitance, hence reducing the dynamic
energy consumption E = CV2=C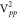 /4,15 i.e., the
energy charged and discharged in a capacitor by an AC voltage with
peak-to-peak voltage Vpp. IL contributes
to optical power loss and signal degradation. The PM figure of merit
(FOMPM) is defined as the product of Vπ and IL (FOMPM = VπαL),16 whereby better phase modulators have a smaller FOMPM.
The modulator BW is critical for Tb/s data transmission, in order
to maximize the data rates that a single channel can support,14 which is
/4,15 i.e., the
energy charged and discharged in a capacitor by an AC voltage with
peak-to-peak voltage Vpp. IL contributes
to optical power loss and signal degradation. The PM figure of merit
(FOMPM) is defined as the product of Vπ and IL (FOMPM = VπαL),16 whereby better phase modulators have a smaller FOMPM.
The modulator BW is critical for Tb/s data transmission, in order
to maximize the data rates that a single channel can support,14 which is  ,17 where BW
is in Hz and S/N is signal-to-noise ratio. e.g., a data rate of 100Gb/s
in a single lane with S/N ≥ 20, which is the
goal set by the 2023 Ethernet Alliance roadmap,7 requires BW ≥ 23 GHz. Table 1 compares the performance of our DSLG modulators
with both graphene and non-graphene based technologies, already commercialized
or showing promise for commercialization.
,17 where BW
is in Hz and S/N is signal-to-noise ratio. e.g., a data rate of 100Gb/s
in a single lane with S/N ≥ 20, which is the
goal set by the 2023 Ethernet Alliance roadmap,7 requires BW ≥ 23 GHz. Table 1 compares the performance of our DSLG modulators
with both graphene and non-graphene based technologies, already commercialized
or showing promise for commercialization.
Table 1. Modulators Based on Si, III–V (InGaAsP), LN, and Graphene for IQ Modulators Designa.
| Ref. | Material | Type | IL [dB] | ER [dB] | VπL [Vcm] | L [cm] | Modulation speed | VπIL [VdB] |
|---|---|---|---|---|---|---|---|---|
| (18) | Si | MZM | 5.4 | 3.6 | 1.4 | 0.2 | 55 GHz | 38 |
| (19) | Si | Ring modulator | 3 | 9.8 | 0.52 | 0.2 | 50 GHz | 8 |
| (20) | Si | Thermo-optic PM | 0.23 | - | 0.027 | 0.006 | 130 kHz | 1 |
| (21) | III–V/Si MOS | MZM depletion mode | - | 11 | 0.24 | 0.05 | 27 GHz | - |
| (22) | III–V/Si MOS | MZM accumulation mode | 1 | 12 | 0.047 | 0.047 | 100 MHz | 1 |
| (23) | III–V/Si MOS | MZM depletion mode | - | 4.4 | 0.3 | 0.03 | 18 GHz | 70 |
| (24) | Thin-film LN | MZM | 0.5 | 30 | 1.4 | 2 | >45 GHz | 0.4 |
| (25) | Thin-film LN | MZM | 7.6 | 20 | 6.7 | 0.5 | 106 GHz | 102 |
| (26) | Thin-film LN/Si | MZM | 2.5 | 40 | 2.2 | 0.3 | >70 GHz | 18.5 |
| (27) | Thin-film LN/Si | MZM | 15 | 19 | 0.8 | 0.3 | >40 GHz | 19.5 |
| (28) | Thin-film LN | Plasmonic MZM | 19.5 | 2.5 | 0.23 | 0.0015 | >10 GHz | 2,990 |
| (29) | DSLG | EAM | 20 | 3 | - | 0.01 | 29 GHz | - |
| (30) | DSLG | Ring modulator | - | 15 | - | 0.003 | 30 GHz | - |
| (31) | DSLG (flakes) | EAM | 4 | 5 | - | 0.006 | 39 GHz | - |
| (32) | SLG/Si | MZM | 10 | 35 | 0.28 | 0.03 | 5 GHz | 62 |
| This work | DSLG | MZM | 5.6 | 25 | 0.3 | 0.0075 | 24 GHz | 3 |
IL does not include coupling losses, but only the excess loss of each device.
Table 1 shows silicon photonics (SiP),18−20 III–V (InGaAsP),21−23 LiNbO3 (LN),24−28 and graphene-based Electro-Absorption Modulators (EAMs)29−31 and PM.32 SiP offers a cost-effective solution for integrating electronic and photonic components in the same circuit by using existing complementary metal oxide semiconductor (CMOS) technology.33 Pure PM is difficult to achieve with Si modulators based on the plasma dispersion effect18,19,34−37 because, due to the Kramers–Kronig relations,38 any change in carrier concentration results in changes in both absorption and phase. Even if pure phase modulators in Si were to be achieved, these devices would rely on doped Si waveguides (WGs), requiring an increased optical power to overcome the additional optical losses introduced by dopants,38 when compared to undoped Si WGs. Other modulation mechanisms in Si can be used, such as the thermo-optic effect,20,39 changing the Si optical properties via electrically induced temperature changes. The thermal time constant of Si is ∼ 1 ms40 at room temperature (RT), limiting operating speeds to the kHz range.20 A comparison between heaters on Si photonic circuits shows that thermo-optic modulators on Si have operating speeds in the kHz range.41 Nonlinear effects, such as the Kerr effect,12 produce a change in refractive index proportional to the product of nonlinear refractive index and intensity of the propagating light.12 But, at telecom wavelengths (1.3, 1.5 μm), this is ∼3 orders of magnitude weaker than the plasma dispersion effect.38 Thus, new materials with higher nonlinear refractive index are needed.
Hybrid approaches that incorporate III–V compounds21−23,42 with doped Si WGs reduce VπL by utilizing other
effects, such as band-filling,43 which
results in reduced absorption due to occupied energy states.44 III–V/Si metal-oxide-semiconductor (MOS)
Mach–Zehnder modulators (MZM) operating in accumulation mode,45 which rely on the change in accumulated charge
carriers within the MOS capacitor by applying a gate voltage, have
the lowest VπL ∼
0.047 Vcm to date,22 with IL ∼ 1
dB,22 but are BW limited to ∼100
MHz.22 III–V/Si MOS MZMs struggle
to maintain VπL = 0.047 Vcm with a higher BW, because of the high (∼3kΩ
μm22) contact resistance22 to the Si electrode in the MOS configuration,
with more moderate values of VπL = 0.24–0.3 Vcm21,23 for III–V
MZMs operating in depletion mode with BW up to ∼27 GHz.21 III–V based MZMs offer a lower VπL compared to Si MZMs,
but at the cost of more complex fabrication, with expensive III–V
processing.46 Cost-effectiveness is determined
by the cost per Watt used to manufacture III–V devices, which
is 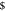 40/W to
40/W to 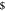 100/W at 2018 prices47,48 at least 2 orders of magnitude higher than Si manufacturing.47,48
100/W at 2018 prices47,48 at least 2 orders of magnitude higher than Si manufacturing.47,48
Integrating LiNbO3 (LN) on undoped Si WGs enables
pure
PM, exploiting the Pockel’s effect,11 producing a change in refractive index proportional to the electric
field. Modulators based on sub-μm thin-film LN,24−27,49 have IL < 1 dB24 and BW > 100 GHz.24,25 Thin-film
LN MZMs were reported with VπL ∼ 1.4 Vcm,24 a factor
of 2 larger than state-of-the-art Si plasma-dispersion MZMs.18 However, this VπL means that cm long devices are needed to reduce Vπ to CMOS compatible levels <1 V.50 Thin-film LN MZMs with VπL ∼ 0.8Vcm27 were demonstrated in the visible range, but with IL ∼
15 dB.27 Plasmonic LN modulators show VπL ∼ 0.23Vcm,28 but with IL ∼ 19.5 dB.28 Modulators with lower VπL and IL are essential to increase the density of
SiP integrated circuits, thus reducing power consumption by minimizing
electrical interconnects. The interconnect losses are frequency (f) dependent (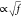 51 ) due to increased
resistance caused by the skin effect,51 where more of the current flows at the surface as f increases.52 Therefore, for electrical
interfaces driving Tb/s data rates, the power consumption of interconnects
becomes the limiting factor.10,51,53
51 ) due to increased
resistance caused by the skin effect,51 where more of the current flows at the surface as f increases.52 Therefore, for electrical
interfaces driving Tb/s data rates, the power consumption of interconnects
becomes the limiting factor.10,51,53
Graphene is ideal for optoelectronics54−57 due to its high carrier mobility (μ > 50000 cm2/V s) at RT,58,59 electrically tunable optical conductivity,60,61 and wavelength independent absorption in the visible (500 nm) to mid-infrared (10 μm).61,62 The gapless band structure with massless Dirac Fermions in single-layer graphene (SLG) enables the optical conductivity to be electrostatically controlled60,61 , and absorption to be suppressed.63 Double SLG (DSLG) phase modulators can reach a theoretical VπL ∼ 0.1 Vcm,64 which enables mm long devices with driving voltages <1 V. When absorption is suppressed, the optical losses can be reduced by orders of magnitude from >1000 dB/cm64 to <10 dB/cm.64 The combination of mm lengths and <10 dB/cm optical losses leads to IL < 1 dB, therefore minimizing power consumption. SLG can be produced at wafer scale.56,65,66 Chemical vapor deposition (CVD) can be used to grow polycrystalline films up to 30″67 or single crystals.68 The latter allows one to fabricate devices at predetermined locations.29,69 SLG films can be integrated in the CMOS back-end-of-line for wafer scale processing after fabrication of the integrated circuits.70 This can reduce cost and complexity of fabrication, by removing the need for doped Si WGs in DSLG designs.29,30,71−73 EAMs,29,31,71,73,74 and electro-refractive modulators30,32,72,75 (ERMs) based on one or more SLG have been reported, with VπL ∼ 0.28 Vcm32 and data transmission rates ∼50Gb/s.29 In SLG-Si modulators, doped Si is used as one plate of the capacitor and this has two main problems: 1) Si dopants increase losses;76 2) The Si mobility (∼1,400 cm2/Vs)77 is lower than SLG, hence limiting operational BW. Among ERMs, pure PM with negligible amplitude modulation was not reported so far in graphene-based devices, to the best of our knowledge.
The SLG conductivity σ(ω), derived from the Kubo formula,78 is a function of the angular frequency of light (ω), SLG transport relaxation time (τ), SLG Fermi level (EF), and temperature T:79−81
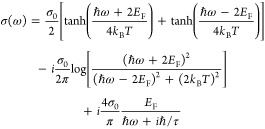 |
1 |
where σ0=e/4ℏ is the f-independent,
or universal conductivity of SLG,62,82 ℏ is
the reduced Planck’s constant, and kB is the Boltzmann constant. The first two terms represent
interband transitions.83,84 The third represents intraband
transitions,83,84 and it is a function of σ0, EF, ω and τ. The
intraband contribution to σ(ω) can be simplified to express
the DC conductivity of SLG (σd.c.) when ω →
0.57 τ can then be related to the
mobility μ by using σd.c.=neμ,85 where n is
the carrier concentration given by EF = 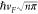 .79,80,86 We thus arrive at
.79,80,86 We thus arrive at 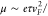 EF(57) for EF ≫ kBT, where
EF(57) for EF ≫ kBT, where 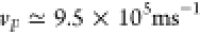 is the Fermi velocity.79,80,83Equation 1 implies that σ(ω) of each SLG depends
on EF, and the energy of the incident
light (Ein = hc/λ).
Absorption in undoped SLG is dominated by interband transitions and
is suppressed when 2EF > hc/λ, due to Pauli blocking.63 For
λ = 1.55 μm, or Ein = 0.8
eV, Pauli blocking occurs for EF >
0.4
eV.
is the Fermi velocity.79,80,83Equation 1 implies that σ(ω) of each SLG depends
on EF, and the energy of the incident
light (Ein = hc/λ).
Absorption in undoped SLG is dominated by interband transitions and
is suppressed when 2EF > hc/λ, due to Pauli blocking.63 For
λ = 1.55 μm, or Ein = 0.8
eV, Pauli blocking occurs for EF >
0.4
eV.
For Pauli blocking, SLG enters the transparency regime,
whereby
interband transitions are suppressed and only intraband transitions
occur.63 Intraband transitions dominate
for low energy photons (ω < 2000 cm–161 ) and for 2EF>hc/λ. Intraband transitions are dependent on τ
because they depend on scattering centers (e.g., defects) for conservation
of momentum.87 Therefore, absorption by
intraband transitions increases for shorter τ, which is related
to mobility 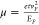 .57
.57
Operating beyond Pauli blocking is essential for pure PM, because in this regime SLG absorption is minimized and constant with respect to gate voltage, thus reducing the overall IL. A DSLG modulator can work as EAM or ERM depending on bias.88 For EAMs, the onset of Pauli blocking results in the largest change in absorption,74 hence the bias should be set at the onset of Pauli blocking. For ERMs, the bias is set beyond the Pauli blocking condition, where the change in refractive index is quasi-linear75 and absorption is minimized.64
Here, we report DSLG-based MZMs on undoped Si WGs operating beyond Pauli blocking with VπL ∼ 0.3 Vcm and pure PM. These work at 16 V without dielectric breakdown, enabling access to the transparency regime. This work represents a key step in the development of graphene-based coherent integrated transmitters for communication systems.
Results and Discussion
The design of our DSLG phase
modulator is in Figure 1a It consists of two SLG encapsulated by
Al2O3, overlapping in the region above the Si
WG. 10 nm Al2O3 encapsulates both SLGs to protect
them during subsequent processing steps, minimize contamination, and
preserve μ. The bottom encapsulation is used to maintain symmetry
between the two SLGs, so that both are in the same environment. Each
SLG is contacted by a metal placed on either side of the WG. The two
SLG layers form a capacitor (equivalent electrical circuit in Figure 1b), where an applied
voltage across the contacts creates a perpendicular electric field
which modulates the carrier density, thus σ(ω) of each
SLG. This, in-turn, modulates the complex effective refractive index, neff,83,84 leading to a change
in phase and absorption of light along the propagation direction.12 We simulate the optical performance of our DSLG
modulators using the Finite-Difference Eigenmode (FDE) solver in Lumerical.89 This uses the expansion method to calculate
the eigenmodes and eigenvalues of Maxwell’s equations in the f domain.90 Each solution, or
mode, has its own electromagnetic field profile and neff.12 The real component is neff, related to the phase, ϕ, of the light
along L by ϕ = k0neffL,12 where k0 (2π/λ0) is the wavenumber in free-space and L is the length of the DSLG modulator. The imaginary component
is the extinction coefficient, κ, related to α, and λ0 as 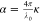 .12
.12
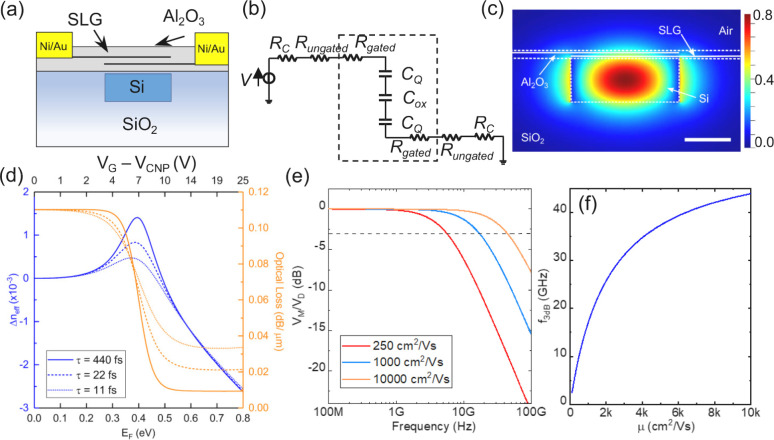
Figure 1.
(a) DSLG modulator scheme, with 20 nm Al2O3 between bottom and top SLG, and fully encapsulating the modulator. (b) Equivalent circuit, used to calculate ZT(ω), ZC(ω), and 3 dB cutoff BW f3dB. The components contained within the dashed line contribute to the impedance of the overlapping SLG section. (c) Simulated Ex of fundamental TE mode confined within a 550 × 220 nm2 Si WG at 1.55 μm. Color scale indicates the Ex amplitude, scale bar 200 nm. (d) Simulated change in neff (blue) and optical loss (orange) of confined mode due to different V–VCNP across the DSLG capacitor. Simulations are performed at 1.55 μm (∼0.8 eV). SLGs are separated by 20 nm Al2O3. The overlapping SLG region is 550 nm, the ungated SLG region is 1 μm (EF = 0.2 eV). (e) Simulated frequency response as a function of μ for a 50 μm DSLG modulator with ungated sections of each SLG ∼ 1 μm (EF ∼ 0.23 eV), gated sections of each SLG ∼ 450 nm (EF ∼ 0.4 eV). RC ∼ 1000 Ω · μm, 20 nm Al2O3 with ϵr = 8, Ceq calculated with an additional carrier concentration ∼1010 cm–2 from defects and ∼1011 cm–2 from charged impurities. μ calculated at 0.4 eV. (f) Simulated f response of DSLG modulator for different μ for the same modulator specification as (e).
The simulated light propagation along the WG shows
the electric
field profile, Figure 1c, of the propagating mode. The mode interaction with SLG is increased
by maximizing the overlap between SLG and field profile. The metal
contacts for each SLG are placed 1 μm away from the WG edge
to avoid optical losses due to proximity of field profile and contacts.
The EO response is simulated by varying EF between 0–0.8 eV and extracting the change in neff as a function of EF. We
use EF ∼ 0.2 eV for ungated SLG,
to account for the impurity doping of as prepared SLG.32,69 Simulations are performed at 300 K for λ = 1.55 μm with
τ = 440,22,11 fs, corresponding to μ ∼ 10000, 500,
250 cm2/(V s) at EF ∼
0.4 eV. We then calculate the phase shift Δϕ = k0ΔneffL and optical losses 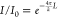 induced by SLG for a given L.12 We relate EF to the applied voltage, V, by considering the sum
of the voltages across the overlapping SLG regions and the surface
voltage due to the accumulated charges at each SLG electrode:50,64
induced by SLG for a given L.12 We relate EF to the applied voltage, V, by considering the sum
of the voltages across the overlapping SLG regions and the surface
voltage due to the accumulated charges at each SLG electrode:50,64
| 2 |
where VCNP is
SLG charge neutrality point. The voltage across the overlapping SLG
region is related to the total number of accumulated charges, ntot, and the equivalent capacitance, Ceq of the overlapping SLG region. Ceq is the series combination of the quantum capacitance,91CQ, of each SLG, and the capacitance of the parallel-plate geometry, Cox. The equivalent electrical circuit of the
DSLG modulator is in Figure 1b. 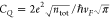 (92,93) and
(92,93) and 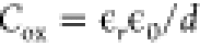 , where d is the thickness
of the gate oxide separating the two SLG, ϵr is the relative permittivity of Al2O3, and ϵ0 is the permittivity of free space. The
dielectric constant of Al2O3 is measured with
a Woollam Ellipsometer M-2000 as
, where d is the thickness
of the gate oxide separating the two SLG, ϵr is the relative permittivity of Al2O3, and ϵ0 is the permittivity of free space. The
dielectric constant of Al2O3 is measured with
a Woollam Ellipsometer M-2000 as 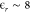 . To account for charged impurities at the
SLG-Al2O3 interface and the impurities introduced
during growth or device fabrication, we model the total charge density n as the sum of a carrier concentration from electrostatic
doping n(VG), with VG the gate voltage, and
that from charged impurities nimp.92 A charged-impurity density 10 12 cm –2(94) leads to an increase
in carrier concentration of SLG ∼ 10 11 cm–2.92 Values of impurity and carrier density
are significant for identifying the ideal working point of graphene
modulators, dictated by EF.57 The presence of impurities increases n, which changes EF. This cannot be neglected, because an additional carrier concentration
∼ 1011cm–2 corresponds to a change EF ∼ 0.1 eV. Hence, the charged impurity
density must be considered when modeling graphene modulators to correctly
identify their working point.
. To account for charged impurities at the
SLG-Al2O3 interface and the impurities introduced
during growth or device fabrication, we model the total charge density n as the sum of a carrier concentration from electrostatic
doping n(VG), with VG the gate voltage, and
that from charged impurities nimp.92 A charged-impurity density 10 12 cm –2(94) leads to an increase
in carrier concentration of SLG ∼ 10 11 cm–2.92 Values of impurity and carrier density
are significant for identifying the ideal working point of graphene
modulators, dictated by EF.57 The presence of impurities increases n, which changes EF. This cannot be neglected, because an additional carrier concentration
∼ 1011cm–2 corresponds to a change EF ∼ 0.1 eV. Hence, the charged impurity
density must be considered when modeling graphene modulators to correctly
identify their working point.
Figure 1d plots
the simulated EO response at 1550 nm in terms of Δneff and associated optical losses per μm with increasing VG and EF. Optical losses decrease when EF > 0.4 eV, corresponding to intraband transitions and the onset
of
Pauli blocking. For EF > 0.4 eV, SLG
enters
the transparency regime, where interband transitions are blocked,
such that optical losses are minimized and do not change as EF is further increased. Δneff changes sign with increasing VG, giving a positive or negative Δϕ
for the modulated signal. A bias voltage can be applied to the DSLG
modulator to define the operating point on the EO response curve in Figure 1d. The amplitude
of the driving voltage defines the operating range around the operating
point. The ideal working point for pure PM is in the transparency
region, where Δneff changes quasi-linearly,
while optical losses remain constant. This also minimizes power consumption,
because optical losses are at their lowest. Optical losses depend
on τ, as plotted in Figure 1d for τ = 440, 22, 11 fs. A low τ is associated
with high scattering rate, Γ, via 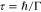 ,79 leading to
increased absorption via intraband transitions and reduced absorption
via interband transitions. As EF approaches
0.4 eV, optical losses are reduced for a lower τ, because absorption
via interband transitions is reduced. However, in transparency, increased
intraband transitions lead to optical losses over 3 times greater
for τ = 11 fs, when compared to 440 fs.
,79 leading to
increased absorption via intraband transitions and reduced absorption
via interband transitions. As EF approaches
0.4 eV, optical losses are reduced for a lower τ, because absorption
via interband transitions is reduced. However, in transparency, increased
intraband transitions lead to optical losses over 3 times greater
for τ = 11 fs, when compared to 440 fs.
The speed of the DSLG phase modulator is defined by the cutoff frequency, f3 dB, at which the power of the modulated signal has decreased by half (3 dB).14 The dominant factor that limits f3 dB is the product of the circuit resistance, R, and capacitance, C, known as the RC response.51 We estimate this by electrical modeling, considering the different contributions to the total circuit impedance ZT(ω), coming from each contact, RC, ungated SLG sections, Rungated, and gated SLG sections, Rgated. The equivalent circuit, Figure 1b, contains these components in series:
| 3 |
Where ZC(ω)
is the impedance of the overlapping SLG regions. ZC(ω) is given by Ceq in series with Rgated for each SLG electrode.
The resistance (R) of SLG can be related to the sheet
resistance (RS) of SLG
as 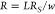 ,54 where L and w the length and width of SLG, respectively.
By considering ω → 0, RS can be related to the electrical conductivity
,54 where L and w the length and width of SLG, respectively.
By considering ω → 0, RS can be related to the electrical conductivity 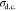 , as
, as  .85RS is calculated for different EF and τ from
.85RS is calculated for different EF and τ from 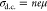 .54RS depends on EF, therefore on the voltage applied across the DSLG modulator. From
Ohm’s law and
.54RS depends on EF, therefore on the voltage applied across the DSLG modulator. From
Ohm’s law and 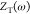 , we calculate the frequency dependent current, I(ω), flowing through the circuit at a nominal drive
voltage, VD,
, we calculate the frequency dependent current, I(ω), flowing through the circuit at a nominal drive
voltage, VD, 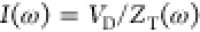 . The voltage drop across the DSLG modulator
following the equivalent circuit in Figure 1b, is:
. The voltage drop across the DSLG modulator
following the equivalent circuit in Figure 1b, is:
| 4 |
which approaches 0 when a current I(ω) is flowing and 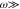 0. Therefore, by substituting I(ω) into
0. Therefore, by substituting I(ω) into 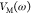 , we get:
, we get:
| 5 |
where 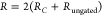 . Figure 1e is the frequency response of our DSLG modulators,
from which the 3 dB cutoff BW can be extrapolated. f3 dB increases with μ in Figure 1f, due to a reduction in Rungated and Rgated for SLG
with higher μ. Assuming a constant μ, f3 dB can be increased by reducing C and R. However, there is a trade-off between minimizing
ungated SLG length, to reduce R, and minimizing the
gated SLG length, to reduce C. Even though Rungated > Rgated, Rgated is of the same order of magnitude
as RC. f3 dB can be further increased by minimizing the distance
between contacts and WG, to minimize the impact from ungated regions.
There is a trade-off between minimizing the required V to reach Pauli blocking and maximizing f3 dB. To reduce V, Cox should
be maximized by using a dielectric with the highest ϵr or reducing d. However, to increase f3 dB, Cox should
be reduced by increasing d and reducing the size
of overlapping SLG region. We limit the size of overlapping SLG to
the WG width and use 20 nm Al2O3 to maximize f3 dB and limit
. Figure 1e is the frequency response of our DSLG modulators,
from which the 3 dB cutoff BW can be extrapolated. f3 dB increases with μ in Figure 1f, due to a reduction in Rungated and Rgated for SLG
with higher μ. Assuming a constant μ, f3 dB can be increased by reducing C and R. However, there is a trade-off between minimizing
ungated SLG length, to reduce R, and minimizing the
gated SLG length, to reduce C. Even though Rungated > Rgated, Rgated is of the same order of magnitude
as RC. f3 dB can be further increased by minimizing the distance
between contacts and WG, to minimize the impact from ungated regions.
There is a trade-off between minimizing the required V to reach Pauli blocking and maximizing f3 dB. To reduce V, Cox should
be maximized by using a dielectric with the highest ϵr or reducing d. However, to increase f3 dB, Cox should
be reduced by increasing d and reducing the size
of overlapping SLG region. We limit the size of overlapping SLG to
the WG width and use 20 nm Al2O3 to maximize f3 dB and limit  15 V. To operate in the transparency regime,
the dielectric should support the required V to reach EF > 0.4 eV without breakdown. Minimizing
the
size of the overlapping SLG region, we reduce the probability of breakdown
due to pinholes in the dielectric.
15 V. To operate in the transparency regime,
the dielectric should support the required V to reach EF > 0.4 eV without breakdown. Minimizing
the
size of the overlapping SLG region, we reduce the probability of breakdown
due to pinholes in the dielectric.
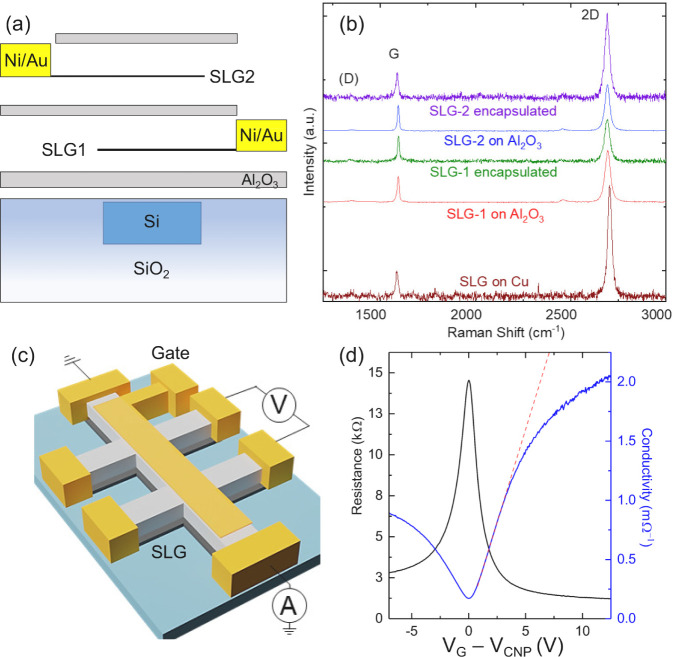
The DSLG modulators are then fabricated as for Figure 2a. We use the IMEC silicon-on-insulator (SOI) platform because of the low (2.3 dB per grating) coupling losses.95 10 nm Al2O3 is deposited on SOI by atomic layer deposition (ALD, Cambridge Nanotech Savannah S100 G1) at 120oC. After a 10 min purge of N2 for contaminants removal, we apply 238 consecutive cycles of 22 ms pulses of deionized water and 17 ms pulses of trimethylaluminum precursors to reach the required 10 nm thickness, as measured with a Woollam Spectroscopic Ellipsometer M-2000XI. Continuous SLG is grown on Cu by CVD. The Cu foil is first annealed at 1050oC under 90% H2 and 10% Ar at 760 Torr for 2h and cooled to RT. To grow SLG, the annealed Cu foil is heated to 1050oC with 40 sccm H2 at 0.4Torr and annealed for 2h. Growth is initiated by introducing 5 sccm CH4 and the CH4 flow is stopped to terminate growth after 30 min, and SLG/Cu is cooled to RT.96 SLG is then wet-transferred using polymethyl-methacrylate (PMMA) as a supporting layer and Cu etching in ammonium persulfate.65
Figure 2.
(a) DSLG modulator fabrication schematic: 10 nm Al2O3 deposition on Si WG with 20 nm Al2O3 between bottom and top SLG. 10 nm Al2O3 is used to encapsulate both SLGs to protect them during subsequent processing steps, minimize contamination, and preserve μ. The bottom encapsulation is used to maintain symmetry between the two SLGs, so that both are in the same environment. (b) Raman spectra at 514 nm for the SLG closest to the WG (SLG1) and that farthest from the WG (SLG2), as-grown on Cu, after transfer, after device fabrication. The spectra are normalized to I(G), with Cu background PL removal.97 (c) Schematic of SLG (gray) on SiO2 (green) top-gated Hall bar with Ni/Au (yellow) contacts. (d) Measured RS (black) and calculated σd.c. (σd.c. = 1RS) (blue). Red dashed line is the σd.c. linear fit for V > 0, showing the transition from linear to sublinear regime for V > 5 V.
As-grown and transferred SLG are characterized
by Raman spectroscopy
with a Renishaw InVia spectrometer equipped with 50× objective
at 514.5 nm. Six spectra are collected from both as grown SLG on Cu
and transferred SLG to estimate doping and defect density. The errors
are calculated from the standard deviation across different spectra,
the spectrometer resolution (∼1 cm–1) and
the uncertainty associated with the different methods to estimate
the doping from full width at half-maximum of G-peak, FWHM (G), intensity
and area ratios of 2D and G peaks, I(2D)/I(G), A(2D)/A(G). Table 2 summarizes the Raman
peaks fits, EF, doping type, charge carrier
density n, strain, and defects density nD. EF is derived from
A(2D)/A(G), I(2D)/I(G) and FWHM(G). First, n is derived
from A(2D)/A(G), I(2D)/I(G) and FWHM(G) for each spectrum by using
experimental values in refs.86,102 producing a value for 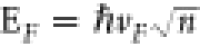 for each spectrum. The final EF is the average of those obtained from each spectrum.
The doping type is derived from Pos(2D).86 For p doping, Pos(2D) increases by ∼20 cm–1,86 while for n doping there is no significant
change until an electron concentration >3 × 1013cm–2 is reached.86 This
doping
dependent behavior of Pos(2D) is used to infer whether SLG is p or
n doped. The strain is derived from Pos(G). Since Pos(G) depends on
both EF and strain, we first derive EF from A(2D)/A(G), I(2D)/I(G) and FWHM(G),
which are independent of strain,63,86,102 and then calculate Pos(G) corresponding to this EF. The strain is then retrieved from the difference
between the experimental and calculated Pos(G): [Pos(G)calc-Pos(G)exp]/ΔPos(G),
with ΔPos(G) ∼ 23 cm–1/% for uniaxial
strain and ∼60 cm–1/% for biaxial strain.105 nD is derived from
I(D)/I(G) for a specific EF, using nD = (2.7 ± 0.8)
for each spectrum. The final EF is the average of those obtained from each spectrum.
The doping type is derived from Pos(2D).86 For p doping, Pos(2D) increases by ∼20 cm–1,86 while for n doping there is no significant
change until an electron concentration >3 × 1013cm–2 is reached.86 This
doping
dependent behavior of Pos(2D) is used to infer whether SLG is p or
n doped. The strain is derived from Pos(G). Since Pos(G) depends on
both EF and strain, we first derive EF from A(2D)/A(G), I(2D)/I(G) and FWHM(G),
which are independent of strain,63,86,102 and then calculate Pos(G) corresponding to this EF. The strain is then retrieved from the difference
between the experimental and calculated Pos(G): [Pos(G)calc-Pos(G)exp]/ΔPos(G),
with ΔPos(G) ∼ 23 cm–1/% for uniaxial
strain and ∼60 cm–1/% for biaxial strain.105 nD is derived from
I(D)/I(G) for a specific EF, using nD = (2.7 ± 0.8) 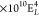 [eV]I(D)/I(G)EF
[eV]I(D)/I(G)EF as derived in ref.103
as derived in ref.103
Table 2. Raman Fit Parameters and Corresponding EF, Doping Type, n, Strain, nD, and Error Bars.
| Samples | SLG1 | Encapsulated SLG1 | SLG2 | Encapsulated SLG2 |
|---|---|---|---|---|
| Pos(G) (cm–1) | 1592 ± 3 | 1596 ± 1 | 1596 ± 1 | 1585 ± 5 |
| FWHM(G) (cm–1) | 14 ± 3 | 12 ± 2 | 11 ± 2 | 17 ± 2 |
| Pos(2D) (cm–1) | 2692 ± 3 | 2691 ± 1 | 2694 ± 2 | 2689 ± 2 |
| FWHM(2D) (cm–1) | 31 ± 1 | 30 ± 1 | 29 ± 3 | 30 ± 4 |
| A(2D)/A(G) (cm–1) | 2.2 ± 0.4 | 5.6 ± 1.7 | 2.7 ± 0.1 | 6.3 ± 0.7 |
| I(2D)/I(G) (cm–1) | 2.7 ± 0.7 | 2.4 ± 1 | 1.8 ± 0.1 | 3.5 ± 0.5 |
| I(D)/I(G) (cm–1) | 0.07 ± 0.03 | 0.03 ± 0.04 | 0.05 ± 0.04 | 0.13 ± 0.13 |
| EF (meV) | 190 ± 80 | 276 ± 158 | 292 ± 87 | 180 ± 130 |
| Doping type | p | p | p | p |
| n (×1012) (cm–2) | 2.6 ± 2.0 | 8.5 ± 9.5 | 5.8 ± 3.2 | 3.9 ± 3.8 |
Uniaxial strain ( ) ) |
-0.20 ± 0.32 | -0.15 ± 0.18 | -0.07 ± 0.17 | 0.08 ± 0.07 |
Biaxial strain ( ) ) |
-0.08 ± 0.14 | -0.06 ± 0.07 | -0.02 ± 0.06 | 0.003 ± 0.02 |
| nD (×1010) (cm–2) | 2.6 ± 0.4 | 1.6 ± 0.9 | 2.5 ± 0.6 | 4.2 ± 2.7 |
The Raman spectrum of as grown SLG is in Figure 2b, after Cu photoluminescence
removal.97 The 2D peak is a single-Lorentzian
with FWHM(2D)
= 27 ± 2 cm–1, signature of SLG.98,99 Pos(G) = 1591 ± 4 cm–1 with FWHM(G) = 16
± 2 cm–1. Pos(2D) = 2712 ± 9 cm–1, I(2D)/I(G) ∼4.5 ± 0.7 and A(2D)/A(G)7.6 ± 1.1.
No D peak is observed, indicating negligible Raman active defects.100,101 First, SLG1 is transferred on 10 nm Al2O3 deposited
on SOI. The representative Raman spectrum of transferred SLG1 before
Al2O3 encapsulation is in Figure 2b. The 2D peak retains its single-Lorentzian
line shape with FWHM(2D) = 31 ± 1 cm–1, Pos(G)
= 1592 ± 3 cm–1, FWHM(G) = 14 ± 3 cm–1, Pos(2D) = 2692 ± 3 cm–1,
I(2D)/I(G) = 2.7 ± 0.7, and A(2D)/A(G) = 2.2 ± 0.4 indicating
a p-doping with EF = 190 ± 80 meV.86,102 I(D)/I(G) = 0.07 ± 0.03 corresponds to a defect density nD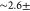 0.4 × 1010103 for excitation energy of 2.41 eV. SLG1 is then patterned
by electron beam lithography (EBL) using a Raith EBPG5200, followed
by a 60s O2 plasma at 10W using a Vision 320 reactive ion
etcher (RIE). Contacts are fabricated using a double-layer resist
mask of methyl methacrylate and PMMA,104 followed by 15/50 nm Ni/Au deposited by sputter coating (Precision
Atomics Metallifier sputter coater) and thermal evaporation (M-Braun
PROvap PVD system). A 1 nm seed-layer of Al is then thermally evaporated,
before 20 nm of Al2O3 is deposited by ALD at
120oC on SLG1. After Al2O3 encapsulation, the 2D peak in SLG1 retains its single-Lorentzian
line shape with FWHM(2D) = 30 ± 1 cm–1, Pos(G)
= 1596 ± 1 cm–1, FWHM(G) = 12 ± 2 cm–1, Pos(2D) = 2691 ± 1 cm–1,
I(2D)/I(G) = 2.4 ± 1, and A(2D)/A(G) = 5.6 ± 1.7 indicating
a p-doping with EF = 276 ± 158 meV.86,102 I(D)/I(G) = 0.03 ± 0.04 corresponds to nD = 1.6 ± 0.9 × 1010103 for 2.41 eV excitation. SLG2 is transferred using the same
process as SLG1, and characterized by Raman spectroscopy (Figure 2b). The 2D peak retains
its single-Lorentzian line shape with FWHM(2D) = 29 ± 3 cm–1. Pos(G) = 1596 ± 1 cm–1, FWHM(G)
= 11 ± 2 cm–1, Pos(2D) = 2694 ± 2 cm–1, I(2D)/I(G) = 1.8 ± 0.1, and A(2D)/A(G) = 2.7
± 0.1, indicating a p-doping with EF = 292 ± 87 meV.86,102 I(D)/I(G) = 0.05 ± 0.04
corresponds to nD = 2.5 ± 0.6 ×
1010103 for 2.41 eV. SLG2 is
then patterned by using O2 plasma after EBL and contacts
are fabricated using a double-layer resist mask for EBL as SLG1, and
subsequent Ni/Au (15/50 nm) deposition. Finally, 10 nm Al2O3 is deposited on SLG2 after a 1 nm Al seed-layer is
thermally evaporated. After Al2O3 encapsulation,
the 2D peak in SLG2 retains its single-Lorentzian line shape with
FWHM(2D) = 30 ± 4 cm–1, Pos(G) = 1585 ±
5 cm–1, FWHM(G) = 17 ± 2 cm–1, Pos(2D) = 2689 ± 2 cm–1, I(2D)/I(G) = 3.5
± 0.5, and A(2D)/A(G) = 6.3 ± 0.7 indicating a p-doping
with EF = 180 ± 130 meV.86,102 I(D)/I(G) = 0.13 ± 0.13 gives nD = 4.2 ± 2.7 × 1010103 for 2.41 eV. SLG1 and SLG2 show different doping and defect density
even though they are transferred from the same SLG/Cu because SLG1
is subject to more fabrication steps than SLG2. Strain is estimated
from Pos(G).105,106 Biaxial strain can be differentiated
from uniaxial by the absence of G-peak splitting with increasing strain,
however at low (≤0.5%) strain the splitting cannot be resolved.
For uniaxial (biaxial) strain, Pos(G) depends on both EF and strain.86,105 To obtain the contribution
of strain only, we first derive EF from
A(2D)/A(G), I(2D)/I(G) and FWHM(G), which are independent of strain,63,86,102 and then calculate Pos(G) corresponding
to this EF. The strain is then retrieved
from the difference between the experimental and calculated Pos (G)
(Table 2).
0.4 × 1010103 for excitation energy of 2.41 eV. SLG1 is then patterned
by electron beam lithography (EBL) using a Raith EBPG5200, followed
by a 60s O2 plasma at 10W using a Vision 320 reactive ion
etcher (RIE). Contacts are fabricated using a double-layer resist
mask of methyl methacrylate and PMMA,104 followed by 15/50 nm Ni/Au deposited by sputter coating (Precision
Atomics Metallifier sputter coater) and thermal evaporation (M-Braun
PROvap PVD system). A 1 nm seed-layer of Al is then thermally evaporated,
before 20 nm of Al2O3 is deposited by ALD at
120oC on SLG1. After Al2O3 encapsulation, the 2D peak in SLG1 retains its single-Lorentzian
line shape with FWHM(2D) = 30 ± 1 cm–1, Pos(G)
= 1596 ± 1 cm–1, FWHM(G) = 12 ± 2 cm–1, Pos(2D) = 2691 ± 1 cm–1,
I(2D)/I(G) = 2.4 ± 1, and A(2D)/A(G) = 5.6 ± 1.7 indicating
a p-doping with EF = 276 ± 158 meV.86,102 I(D)/I(G) = 0.03 ± 0.04 corresponds to nD = 1.6 ± 0.9 × 1010103 for 2.41 eV excitation. SLG2 is transferred using the same
process as SLG1, and characterized by Raman spectroscopy (Figure 2b). The 2D peak retains
its single-Lorentzian line shape with FWHM(2D) = 29 ± 3 cm–1. Pos(G) = 1596 ± 1 cm–1, FWHM(G)
= 11 ± 2 cm–1, Pos(2D) = 2694 ± 2 cm–1, I(2D)/I(G) = 1.8 ± 0.1, and A(2D)/A(G) = 2.7
± 0.1, indicating a p-doping with EF = 292 ± 87 meV.86,102 I(D)/I(G) = 0.05 ± 0.04
corresponds to nD = 2.5 ± 0.6 ×
1010103 for 2.41 eV. SLG2 is
then patterned by using O2 plasma after EBL and contacts
are fabricated using a double-layer resist mask for EBL as SLG1, and
subsequent Ni/Au (15/50 nm) deposition. Finally, 10 nm Al2O3 is deposited on SLG2 after a 1 nm Al seed-layer is
thermally evaporated. After Al2O3 encapsulation,
the 2D peak in SLG2 retains its single-Lorentzian line shape with
FWHM(2D) = 30 ± 4 cm–1, Pos(G) = 1585 ±
5 cm–1, FWHM(G) = 17 ± 2 cm–1, Pos(2D) = 2689 ± 2 cm–1, I(2D)/I(G) = 3.5
± 0.5, and A(2D)/A(G) = 6.3 ± 0.7 indicating a p-doping
with EF = 180 ± 130 meV.86,102 I(D)/I(G) = 0.13 ± 0.13 gives nD = 4.2 ± 2.7 × 1010103 for 2.41 eV. SLG1 and SLG2 show different doping and defect density
even though they are transferred from the same SLG/Cu because SLG1
is subject to more fabrication steps than SLG2. Strain is estimated
from Pos(G).105,106 Biaxial strain can be differentiated
from uniaxial by the absence of G-peak splitting with increasing strain,
however at low (≤0.5%) strain the splitting cannot be resolved.
For uniaxial (biaxial) strain, Pos(G) depends on both EF and strain.86,105 To obtain the contribution
of strain only, we first derive EF from
A(2D)/A(G), I(2D)/I(G) and FWHM(G), which are independent of strain,63,86,102 and then calculate Pos(G) corresponding
to this EF. The strain is then retrieved
from the difference between the experimental and calculated Pos (G)
(Table 2).
A
4-point-probe measurement using top-gated Hall bar structures
(Figure 2c) is performed
to derive SLG resistance and conductivity. Figure 2d plots the measured voltage-dependent resistance
and the calculated σd.c. after normalizing the conductance
to the channel geometry. We observe the expected107 peak in resistance, which corresponds to the SLG Dirac
point. μ is estimated from the measured conductivity as σd.c. 85,107 where the linear region
of σd.c. in Figure 2d corresponds to a constant μ. The charge density n in terms of Cox
85,107 where the linear region
of σd.c. in Figure 2d corresponds to a constant μ. The charge density n in terms of Cox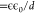 can be written as
can be written as 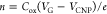 ,107 hence the
conductivity becomes σd.c.
,107 hence the
conductivity becomes σd.c.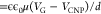 . Using measured dielectric constant and
thickness of
. Using measured dielectric constant and
thickness of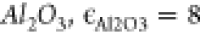 and d = 20 nm, the measured σd.c. can be fitted to estimate
and d = 20 nm, the measured σd.c. can be fitted to estimate 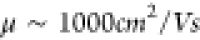 . The linear fit to SLG conductivity as
a function of VG is in Figure 2d.
. The linear fit to SLG conductivity as
a function of VG is in Figure 2d.
The EO response of
DSLG EAMs and ERMs are then measured using angled
single-mode optical fibers to couple light into the photonic circuits
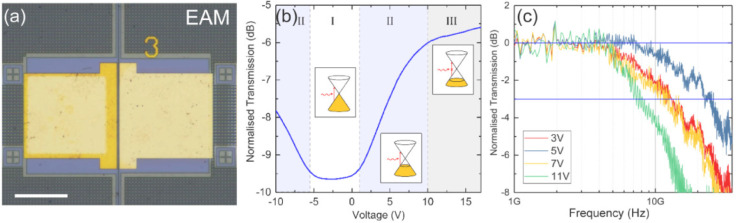
via grating couplers. A representative EAM optical microscopy image
in Figure 3a. The position
of the fibers and the polarization of the source laser (Agilent 8164B
Lightwave Measurement System) are adjusted to minimize coupling losses
and maximize the power coupled into the confined optical mode. The
steady-state response is measured by applying a DC voltage across
both SLGs and measuring the optical power at the output, Pout. The transmitted power, Pt = 10 log(Pout/Pin), is expressed in dB. Figure 3b is the optical transmission of a DSLG EAM comprising
a 75 μm modulator on a straight WG. The EAM is biased between
−10 and 17 V at 1.55 μm with Pin = 1 mW. To extract IL, Pt needs to be
normalized to account for the additional propagation and coupling
losses introduced from processing. The increase in power loss, compared
to the loss before processing, is due to the deposited Al2O3 on the grating couplers, residues from SLG transfer
and device fabrication. The additional losses can be subtracted by
measuring the transmission through a similar WG, with same dimensions
and grating couplers, that has undergone the same processing steps
as the DSLG modulator. The lowest VG dependent
transmission in EAM occurs in region I in Figure 3b, between −5 and 0 V, when EF is less than the half of the photon energy, 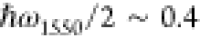 eV. Therefore, interband transitions in
SLG are allowed in region I. The transmitted power is minimum in this
voltage range around VCNP where EF is closer to Dirac point.61 For intrinsic SLG, where VCNP coincides with VG = 0, the
transmission curve would be centered at 0 V. In Figure 3b the VCNP is
∼−2.5 V. This corresponds to EF ∼ 274 meV, which represents the average EF of both SLGs in the DSLG EAM. This is also consistent
with the average SLGs EF
eV. Therefore, interband transitions in
SLG are allowed in region I. The transmitted power is minimum in this
voltage range around VCNP where EF is closer to Dirac point.61 For intrinsic SLG, where VCNP coincides with VG = 0, the
transmission curve would be centered at 0 V. In Figure 3b the VCNP is
∼−2.5 V. This corresponds to EF ∼ 274 meV, which represents the average EF of both SLGs in the DSLG EAM. This is also consistent
with the average SLGs EF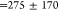 meV, estimated from Raman spectroscopy
of SLG1 and SLG2 after Al2O3 encapsulation (Table 2, Figure 2b). As VG increases in region II, EF approaches
meV, estimated from Raman spectroscopy
of SLG1 and SLG2 after Al2O3 encapsulation (Table 2, Figure 2b). As VG increases in region II, EF approaches 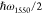 , and transmission increases due to Pauli
blocking of interband transitions. For VG > 10 V, the transmission plateaus when EF
, and transmission increases due to Pauli
blocking of interband transitions. For VG > 10 V, the transmission plateaus when EF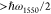 and SLG enters the transparency regime.
and SLG enters the transparency regime.
Figure 3.
(a) Optical micrograph of EAM consisting of DSLG modulator on straight Si WGs. Scale bar 50 μm. (b) EO response of a 75 μm DSLG EAM showing the different regimes depending on EF. At 1.55 μm, transmission is lowest in region I (white), when EF < 0.4 eV. It increases in region II (blue) due to the onset of Pauli blocking, when EF approaches 0.4 eV, before transitioning to the minimum-loss regime in region III (gray) > 10 V, where EF > 0.4 eV. The Si WG is 450 × 220 nm2. (c) EO frequency response for a 50 μm DSLG EAM at different DC biases with a 1 V peak-to-peak driving voltage. f3dB ∼ 13 GHz for 3 V, 24 GHz for 5 V, 12 GHz for 7 V, and 8 GHz for 11 V.
In transparency, IL ∼ 5.6 dB for the DSLG phase modulator, corresponding to loss ∼746 dB/cm when normalized by the modulator length. This is higher than state-of-the-art Si depletion (∼22 dB/cm),18 III–V (∼19 dB/cm),22 LN (∼0.25 dB/cm),24 and SLG (∼236 dB/cm32) MZMs (Table 1). We attribute the additional optical losses to scattering from resist residues and defects generated in SLG during fabrication, degrading τ. The simulated optical loss of the same device structure is ∼93 dB/cm for τ = 440 fs. Therefore, IL can be further reduced by improving SLG processing, increasing μ, hence reducing short-range scattering, and by developing a selective planarization process which isolates passive sections of the WGs. By modifying the thickness of the oxide layer between SLG and Si core, we can tune light-matter interactions between the Si core evanescent tail and SLG. This also applies to Cu and polymer residues which might be present. By fabricating a thick (>1 μm) oxide layer in the regions where there are no modulators (passive regions), it is possible to reduce light-matter interactions between contaminants and WG, hence reducing optical losses. At the same time, by placing a thin (<50 nm) oxide layer between SLG and WG in the regions where modulators are present (active regions), it is possible to increase ER. The size of overlapping SLG regions can be increased to further reduce IL, as the ungated SLG sections are not in transparency, hence contributing optical losses. However, any increase in the overlapping SLG region, will increase Ceq, therefore will reduce f3 dB. Increasing the overlapping SLG region to ∼1 μm, would decrease optical loss to <10 dB/cm for τ = 440 fs, leading to IL < 1 dB for ∼3 mm devices, matching IL of LN60 and III–V22 MZMs (Table 1).
The EO BW, or speed, is then measured by applying a sinusoidal voltage to the DSLG modulators, in either EAM or ERM configuration. The voltage is provided by a signal generator (Agilent E8257D PSG) combined with a DC voltage via a bias tee. The optical output from the DSLG modulator is then amplified with an Er doped fiber amplifier (EDFA, Keopsys CEFA-C-HG) followed by a 1 nm narrow-band optical filter, before going into a InGaAs photodetector (PD) with a BW > 40 GHz (Newport 1014). The narrow-band filter is used to remove the noise resulting from the spontaneous emission from the EDFA,108 and to ensure that the PD input power is below the safe input power = 5 mW given by the specifications of the Newport PD.109 The modulated output signal is recorded on an electrical spectrum analyzer (ESA, Agilent PSX N9030A). By monitoring the amplitude of the modulated signal with increasing f, we get f3 dB. The setup is calibrated by repeating the measurements with the same configuration, but with a Thorlabs LN05S-FC AM with a 3 dB cutoff ∼40 GHz. A final normalization is then done for the f response of the Thorlabs LN05S-FC modulator, taken from the supplied data sheet.110Figure 3c is the f response of a 50 μm DSLG EAM for different DC biases. f3 dB increases from 13 to 25 GHz between 3 and 5 V, then decreases to 12 GHz for 7 V, and 8 GHz for 11 V. We attribute the decrease in f3 dB above 5 V to a reduction in μ due to increased short-range scattering of charge carriers as EF increases. For our RC limited devices, we expect f3 dB to increase with V, because RS reduces with increasing V,107 up to an optimum point after which the increase of Cq becomes predominant. The optimal bias point for operating our device at 25 GHz BW is ∼5V, while operating it at CMOS-compatible voltages (<2 V) allows 13 GHz, Figure 3c. We assign the VG-dependent slow-down in Figure 3c to a decrease in μ above 5 V due to increased short-range scattering as VG increases. This would lead to a f3 dB slow-down of the same order of magnitude as that measured between 5 and 11 V, where f3 dB drops from 25 to 8 GHz. This contrasts the increase from 13 to 25 GHz between 3 and 5 V, where we are still in the linear region of σd.c., and benefit from decreasing RS. The transition to sublinear behavior can be pushed to higher VG by decreasing the sources of short-range scattering in SLG, from SLG processing improvements. Thus, f3 dB can be increased by improving SLG growth and transfer, to limit μ degradation during fabrication. We attribute the observed 17 GHz variation in BW at different Vg not only to the variation of μ, but also contact resistance, as we change Vg. μ is voltage-dependent, with a minimum at the Dirac point (charge neutrality point VCNP). When changing the working point of the modulator by varying the driving voltage, we modify μ too.111 This directly impacts the RC response of the modulator, hence its BW f3 dB = 1/2πRC. However, the observed variation in BW cannot be explained solely by the change in μ, as 17 GHz magnitude of variation was not previously reported for other SLG modulators, to the best of our knowledge. There is, thus, also a gate-dependent contact resistance contribution, that we observe because hundreds Ω change in resistance R could change f3dB = 1/2πRC by 17 GHz.
The simultaneous phase change that accompanies
the change of amplitude
cannot be extracted from an electro-absorption configuration, because
the transmission of a straight WG is independent of optical signal
phase.12 Instead, it is measured using
an electro-refractive configuration, with a Mach–Zehnder interferometer
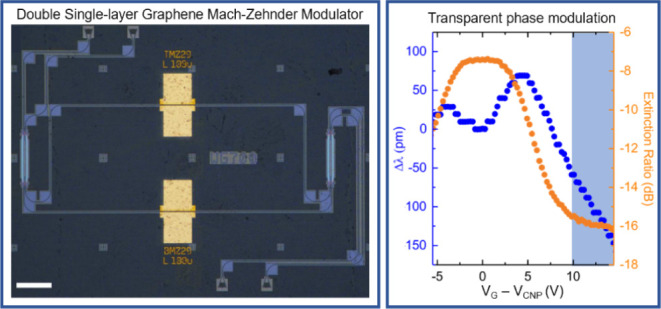
(MZI).12,112 The optical microscopy image of a representative
MZI is in Figure 4a.
Here, the optical signal is split into two arms. Depending on the
phase difference between these, Δϕ, the propagating waves
will interfere when recombined. If the propagating waves are in phase,
transmission will not depend on λ.12 If they are not in phase, an interference pattern will appear.12 In our case we have an unbalanced MZI and transmission
is wavelength-dependent, hence an interference pattern will appear.
This is characterized by the free spectral range 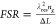 ,112 defined
as the wavelength difference between each transmission minima, where
λ res is the fringe position, ng is the group index, and ΔL is the length difference between the arms of the MZI. λ res depends on Δϕ, which can result from a modulator
that induces Δneff, or when the
MZI arms are different lengths, known as an unbalanced MZI.13 A MZM uses an ERM on one or both MZI arms to
control Δϕ. Δϕ can then be directly measured
by the shift of the output interference pattern.12 Placing an ERM on each arm enables the phase to be controlled
independently on each arm to reach the required Δϕ. Figure 4b shows the V-dependent
frince shift, Δλ, and extinction ratio (ER) of a MZM
with a 100 μm DSLG modulator on each arm of an unbalanced MZI.
One device is biased at 10 V, so that it is in the transparency regime,
and the other is swept from 4 to 10 V. By measuring Δλ
for different VG, we determine Δϕ,
shown in Figure 4c.
The measured Δλ is normalized by the FSR, which corresponds
to a phase difference of 2π,12 giving
Δϕ in units of π:
,112 defined
as the wavelength difference between each transmission minima, where
λ res is the fringe position, ng is the group index, and ΔL is the length difference between the arms of the MZI. λ res depends on Δϕ, which can result from a modulator
that induces Δneff, or when the
MZI arms are different lengths, known as an unbalanced MZI.13 A MZM uses an ERM on one or both MZI arms to
control Δϕ. Δϕ can then be directly measured
by the shift of the output interference pattern.12 Placing an ERM on each arm enables the phase to be controlled
independently on each arm to reach the required Δϕ. Figure 4b shows the V-dependent
frince shift, Δλ, and extinction ratio (ER) of a MZM
with a 100 μm DSLG modulator on each arm of an unbalanced MZI.
One device is biased at 10 V, so that it is in the transparency regime,
and the other is swept from 4 to 10 V. By measuring Δλ
for different VG, we determine Δϕ,
shown in Figure 4c.
The measured Δλ is normalized by the FSR, which corresponds
to a phase difference of 2π,12 giving
Δϕ in units of π: 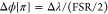 .72 Δϕ
is related to the V-induced change in the real component of neff along L, by Δϕ
= k0ΔneffL.12
.72 Δϕ
is related to the V-induced change in the real component of neff along L, by Δϕ
= k0ΔneffL.12
Figure 4.
(a) Optical micrograph
of MZM consisting of a DSLG modulator on
each arm of a Si MZI. Scale bars 100 μm. (b) Voltage-dependent
shift of interference fringe position (blue) and ER (orange) of an
MZM with a ∼100 μm DSLG modulator on each arm, with one
modulator biased at 10 V. The MZI is unbalanced, with 2 input and
output ports, and 620 × 220 nm2 Si WGs. (c) Phase
shift as a function of voltage for a 100 μm long modulator.
(d) Comparison of measured (solid circles) and simulated (open circles)
Δneff (blue) and Δα
(orange) for a 450 μm DSLG MZM. Simulation performed at 1.55
μm with τ = 14 fs, same device structure as the measured
device, 550 × 220 nm2 Si WG, overlapping SLG region
∼550 nm, ungated SLG region ∼1 μm (EF = 0.2 eV), 20 nm Al2O3 with 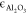 = 8. (e) Voltage-dependent transmission
of a MZM containing one 450 μm DSLG modulator on each arm, one
biased at 10 V and the other swept from 4.7 V (orange) to 9.6 V (red).
(f) Voltage-dependent shift of interference fringe position (blue)
and ER (orange) of an MZM with a ∼450 μm DSLG modulator
on each arm, with one modulator biased at 10 V.
= 8. (e) Voltage-dependent transmission
of a MZM containing one 450 μm DSLG modulator on each arm, one
biased at 10 V and the other swept from 4.7 V (orange) to 9.6 V (red).
(f) Voltage-dependent shift of interference fringe position (blue)
and ER (orange) of an MZM with a ∼450 μm DSLG modulator
on each arm, with one modulator biased at 10 V.
The extinction ratio (ER) =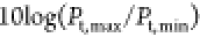 ,13 where P(t,max) is the maximum transmitted power and P(t,min) the minimum transmitted power, is affected
by the difference in absorption between the MZI arms, Δα.
Simulated and measured Δneff and
Δα are shown in Figure 4d. If the propagating wave in one arm is absorbed,
there is no interference at the output, because there will only be
one propagating wave remaining.12 For losses
that do not result in complete absorption, ER will increase when Δα
is minimized, and decrease when Δα is maximized. The MZM
ER can be related to Δα by considering the transmission
through the MZM as the sum of the electric fields propagating down
each MZI arm:
,13 where P(t,max) is the maximum transmitted power and P(t,min) the minimum transmitted power, is affected
by the difference in absorption between the MZI arms, Δα.
Simulated and measured Δneff and
Δα are shown in Figure 4d. If the propagating wave in one arm is absorbed,
there is no interference at the output, because there will only be
one propagating wave remaining.12 For losses
that do not result in complete absorption, ER will increase when Δα
is minimized, and decrease when Δα is maximized. The MZM
ER can be related to Δα by considering the transmission
through the MZM as the sum of the electric fields propagating down
each MZI arm:  .12,112 ER is given by the
ratio of maximum and minimum transmission through the MZM, which occurs
when Δϕ = 0 and π:12
.12,112 ER is given by the
ratio of maximum and minimum transmission through the MZM, which occurs
when Δϕ = 0 and π:12
| 6 |
Figure 4e,f show that, as VG increases, and the SLG on the active arm becomes transparent,
ER increases >25 dB because Δα is reduced. The effect
of Δϕ and Δα due to the active arm of the
MZM is seen by the simultaneous change in position and ER of the interference
fringes with VG. Figure 4f plots the change
in position of interference fringe and ER as a function of VG. The MZM has the same behavior
as the EAM in Figure 3. ER is minimized near the Dirac point, because the absorption of
the SLG on the active arm is highest, while the device on the other
arm is transparent. ER then increases with increasing VG, as absorption by the active arm is
reduced, until flattening >10 V, when the SLGs on both arms are
transparent.
This shows that the transparency regime is ideal for pure PM because
we have a quasi-linear change in phase, while losses remain constant.
A similar V-dependent change in fringe position and ER is observed
on either side of the Dirac point, where negative VG give a weaker effect than positive ones. The similarity around
the Dirac point is due to the SLG ambipolarity,107 and the asymmetry can be due to different scattering rates
of electrons (e) and holes (h),
resulting from an uneven distribution of positively or negatively
charged impurities.94,113−115 From Δλ and ΔER we extract Δneff and Δα, Figure 4d. The measured and simulated Δneff and Δα are in Figure 4d. We attribute the differences
in measured and simulated behavior to asymmetries between the two
SLG as each SLG undergoes different amounts of processing, since SLG1
is subject to more processing than SLG2. The difference between measured
and simulated Δα in transparency is a result of increased
propagation losses outside the DSLG modulator, due to residues remaining
on the WG from SLG processing. Values of ΔΦ calculated
in transparency for a 100 μm long modulator range from −0.01π
at 8 V to −0.16π at 13.8 V, which give a VπL ∼ 0.3 Vcm, matching that
of state-of-the-art SLG PMs.32 However,
unlike ref (32), our
devices have pure PM with negligible change in optical losses, an
essential property for IQ modulation.11VπL is obtained from ΔΦ
as follows. The Mach–Zehnder interferometer free spectral range
(FSR) is 1.86 nm, as derived from Figure 4e, then 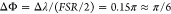 using the wavelength shift in Figure 4b Δλ
= 142 pm from 8 to 13.8 V. The formula used to calculate the phase
shift is
using the wavelength shift in Figure 4b Δλ
= 142 pm from 8 to 13.8 V. The formula used to calculate the phase
shift is 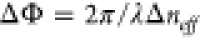 L, with Δneff = λ2/(FSR × L). This
phase shift corresponds to a modulation efficiency VπL = ΔV/ΔΦ L = 0.3 Vcm, for L = 100 μm, calculated in
a range where SLG absorption is negligible, as shown in Figure 4b for VG-
L, with Δneff = λ2/(FSR × L). This
phase shift corresponds to a modulation efficiency VπL = ΔV/ΔΦ L = 0.3 Vcm, for L = 100 μm, calculated in
a range where SLG absorption is negligible, as shown in Figure 4b for VG-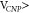 8 V. PM with negligible AM only occurs in
the voltage range ∼10–13 V in Figure 4b. The modulation efficiency of 0.3Vcm also
considers the phase shift which occurs in the AM regime. In addition,
we directly measure up to ΔΦ = Δλ/(FSR/2)
= 0.6
8 V. PM with negligible AM only occurs in
the voltage range ∼10–13 V in Figure 4b. The modulation efficiency of 0.3Vcm also
considers the phase shift which occurs in the AM regime. In addition,
we directly measure up to ΔΦ = Δλ/(FSR/2)
= 0.6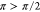 , with Δλ = 650 pm from 5 to
10 V, in a device where AM is not negligible. The latter wavelength
shift is taken from Figure 4e,f. Our modulators with L = 450 μm
can achieve π phase shift if driven in a push–pull configuration,116 while increasing L to 0.6
cm would enable a 2π phase shift. Our DSLG MZMs have a VπL on par with the lowest
reported plasmonic LN MZMs,28 ∼5
times better than the lowest reported LN MZMs,49 and ∼2.5 times better than the lowest reported thin
film LN MZMs27 and Si MZMs18 (Table 1). Due to the high (∼746 dB/cm) optical loss, our DSLG phase
modulator has FOMPM > 200VdB, greater than the lowest
reported
Si (∼38VdB),18 LN (∼0.35VdB),24 and III–V (∼1VdB22) (Table 1). However, if the optical losses of SLG in transparency are reduced
<10 dB/cm by increasing the overlapping SLG region and increasing
τ to >300 fs, corresponding to μ > 6,000 cm2V–1s–1, our low VπL would enable FOMPM ∼ 3VdB. This is a realistic perspective, because
we reported
an average
, with Δλ = 650 pm from 5 to
10 V, in a device where AM is not negligible. The latter wavelength
shift is taken from Figure 4e,f. Our modulators with L = 450 μm
can achieve π phase shift if driven in a push–pull configuration,116 while increasing L to 0.6
cm would enable a 2π phase shift. Our DSLG MZMs have a VπL on par with the lowest
reported plasmonic LN MZMs,28 ∼5
times better than the lowest reported LN MZMs,49 and ∼2.5 times better than the lowest reported thin
film LN MZMs27 and Si MZMs18 (Table 1). Due to the high (∼746 dB/cm) optical loss, our DSLG phase
modulator has FOMPM > 200VdB, greater than the lowest
reported
Si (∼38VdB),18 LN (∼0.35VdB),24 and III–V (∼1VdB22) (Table 1). However, if the optical losses of SLG in transparency are reduced
<10 dB/cm by increasing the overlapping SLG region and increasing
τ to >300 fs, corresponding to μ > 6,000 cm2V–1s–1, our low VπL would enable FOMPM ∼ 3VdB. This is a realistic perspective, because
we reported
an average 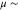 8,000 cm2/(V s) for CVD SLG transferred
on Si in ref.117 This
is 800% higher than that used here. By inserting this μ in our
simulations, we get optical losses ∼9.46 dB/cm. FOMPM ∼ 3VdB is lower than both Si and LN MZMs, with ∼3
mm devices instead ∼2 cm. Even though III–V MZMs have
the lowest FOMPM ∼ 1VdB,22 their BW is unsuitable for Tb/s data transmission because it is
limited to the MHz range.22 Shrinking device
dimensions by 1 order of magnitude results in denser circuits that
benefit from reduced overall power consumption by minimizing the interconnects
lengths.
8,000 cm2/(V s) for CVD SLG transferred
on Si in ref.117 This
is 800% higher than that used here. By inserting this μ in our
simulations, we get optical losses ∼9.46 dB/cm. FOMPM ∼ 3VdB is lower than both Si and LN MZMs, with ∼3
mm devices instead ∼2 cm. Even though III–V MZMs have
the lowest FOMPM ∼ 1VdB,22 their BW is unsuitable for Tb/s data transmission because it is
limited to the MHz range.22 Shrinking device
dimensions by 1 order of magnitude results in denser circuits that
benefit from reduced overall power consumption by minimizing the interconnects
lengths.
Conclusions
We reported DSLG MZMs showing pure PM in the transparency regime for EF > 0.4 eV, with VπL ∼ 0.3Vcm. We reached the transparency regime by device design and process optimization, ensuring the dielectric can withstand the required 10 V to reach EF > 0.4 eV without breakdown. Compared to SLG on Si phase modulators,32 our work has reduced IL from 10 to 5 dB, while maintaining the same modulation efficiency, and almost doubled BW, while operating the device in transparency (5 to 8 GHz). By operating our devices in the regime where also AM occurs, our BW is 5 times larger than ref.32 The decrease in optical loss is due to the DSLG structure, which does not require Si doping, thus avoiding associated losses. Indeed, the DSLG structure can be integrated on any passive photonic platform, making it an enabling low-cost technology. We measured up to π/2 phase shift, enough for applications such as binary phase shift keying.118 A full 2π phase shift can be achieved with L = 0.6 cm. Our work represents a significant step forward compared to the SLG-Si modulator architecture, since it enables the use of purely passive Si WG, hence reducing losses, with BW determined by the SLG μ.75 Our low VπL = 0.3Vcm means we are able to overcome the loss limitations of Si MZMs, deliver increased circuit densities compared to LN, and match the performance of III–V (InGaAsP) MZMs, without expensive fabrication requirements. Reaching transparency is critical for graphene-based communications and metrology platforms that use complex modulation formats to maximize the density of transmitted information.
Methods
Simulations
The electro-optic response is simulated
with the FDE solver in Lumerical Mode, an open-source electromagnetic
modeling software.119 SLG is modeled with
the surface conductivity model available in the software (eq 1), derived from Kubo’s
formalism.78 The frequency response is
simulated by analytically solving the equivalent electrical circuit
characteristics of the modulator, considering the different contributions
to the total circuit impedance, 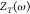 , coming from both metallic contacts and
SLG. For FDE simulations, we use a minimum mesh step size of 10 nm,
perfect matching layer (PML) boundary conditions to minimize reflections,
and a local mesh of 1 nm step, overriding the larger mesh where SLG
is located.
, coming from both metallic contacts and
SLG. For FDE simulations, we use a minimum mesh step size of 10 nm,
perfect matching layer (PML) boundary conditions to minimize reflections,
and a local mesh of 1 nm step, overriding the larger mesh where SLG
is located.
Fabrication
The fabrication of the DSLG modulators is as follows. First, we deposit 10 nm alumina by thermal atomic layer deposition (ALD, Cambridge Nanotech Savannah S100 G1) on the SOI platform at 120◦C, then we grow SLG by CVD on Cu and we transfer it on SOI using PMMA as supporting layer. SLG is shaped by oxygen plasma etching and metallized by thermal evaporation of Ni and Au after EBL (EBPG Raith 5200). Alumina deposition, SLG transfer, shaping and metallization steps are repeated to finalize the fabrication of the DSLG modulator. A final deposition of alumina is done to encapsulate the DSLG structure.
Electrical and Optoelectronic Characterization
Electrical characterization is done by 4-probe measurements using a semiautomatic Cascade probe station on top-gated Hall Bar devices to measure resistance, conductivity, and μ. Optoelectronic characterization is done with a custom fiber-to-chip setup employing source-measure units for DC electrical probing, a telecom C-band laser, commercial photodiodes, one RF signal generator connected to 40 GHz RF probes, and an electrical spectrum analyzer to monitor the transmitted electrical power.
Acknowledgments
We acknowledge funding from EU Graphene Flagship, ERC Grants Hetero2D, GIPT, EU Grants GRAPH-X, CHARM, EPSRC Grants EP/K01711X/1, EP/K017144/1, EP/N010345/1, EP/L016087/1, EP/V000055/1, EP/X015742/1, Nokia Bell Laboratories, DSTL, and MUR—Italian Minister of University and Research under the “Research projects of relevant national interest-PRIN 2020-Project No. 2020JLZ52N “Light-matter interactions and the collective behavior of quantum 2D materials (q-LIMA)″. For the purpose of open access, the authors applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising. Data can be accessed here: 10.17863/CAM.111357.
Author Contributions
The authors declare no competing financial interest.
References
- Cisco Cisco Visual Networking Index: forecast and Trends 2017–2022; Cisco, 2019. [Google Scholar]
- Stocker V.; Lehr W.; Smaragdakis G.. COVID-19 and the Internet: Lessons Learned. In Beyond the Pandemic? Exploring the Impact of COVID-19 on Telecommunications and the Internet, Whalley J.; Stocker V.; Lehr W., Eds.; Emerald Publishing Limited: Leeds; 2023, pp. 17–69.. [Google Scholar]
- Feldmann A.; Gasser O.; Lichtblau F.; Pujol E.; Poese I.; Dietzel C.; Wagner D.; Wichtlhuber M.; Tapiador J.; Vallina-Rodriguez N.; Hohlfeld O.; Smaragdakis G.. Implications of the COVID-19 Pandemic on the Internet Traffic. Broadband Coverage In Germany; 15th ITG-Symposium; IEEE, 2021, 1–5.. [Google Scholar]
- Marcus J. S.COVID-19 and the Shift to Remote Work. In Beyond the Pandemic? Exploring the Impact of COVID-19 on Telecommunications and the Internet, Whalley J.; Stocker V.; Lehr W., Eds.; Emerald Publishing Limited: Leeds, 2023; pp. 71–102.. [Google Scholar]
- Ericsson. Ericsson Mobility Report; Ericsson; 2020. [Google Scholar]
- IEEE Standards Association. IEEE Standard for Ethernet; IEEE. https://standards.ieee.org/ieee/802.3/7071/, 2018. [Google Scholar]
- Ethernet Alliance. Ethernet Roadmap; Ethernet Alliance. https://ethernetalliance.org/technology/ethernet-roadmap/, 2023. [Google Scholar]
- Wei J.; Cheng Q.; Penty R.; White I. H.; Cunningham D. 400 Gigabit Ethernet Using Advanced Modulation Formats: Performance, Complexity, and Power Dissipation. IEEE Commun. Mag. 2015, 53, 182–189. 10.1109/MCOM.2015.7045407. [DOI] [Google Scholar]
- Sharif M.; Perin J. K.; Kahn J. M. Modulation Schemes for Single-Laser 100 Gb/s Links: Single-Carrier. J. Light. Technol. 2015, 33 (20), 4268–4277. 10.1109/JLT.2015.2470523. [DOI] [Google Scholar]
- Miller D. Rationale and Challenges for Optical Interconnects to Electronic Chips. Proc. IEEE 2000, 88, 728–749. 10.1109/5.867687. [DOI] [Google Scholar]
- Kumar S.; Deen M. J.. Fiber Optic Communications: Fundamentals and Applications; Wiley: Hoboken, 2014. [Google Scholar]
- Reed G. T.; Knights A. P.. Silicon Photonics: An Introduction; Wiley: Chichester, 2004. [Google Scholar]
- Reed G.Silicon Photonics: The State of the Art. In Silicon Photonics; Reed G., Eds.; Wiley: Chichester, 2008. [Google Scholar]
- Reed G. T.; Mashanovich G.; Gardes F. Y.; Thomson D. J. Silicon Optical Modulators. Nat. Photonics 2010, 4, 518–526. 10.1038/nphoton.2010.179. [DOI] [Google Scholar]
- Ye S. W.; Yuan F.; Zou X.; Shah M. K.; Lu R.; Liu Y. High-speed optical phase modulator based on graphene-silicon waveguide. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 76–80. 10.1109/JSTQE.2016.2545238. [DOI] [Google Scholar]
- Tu X.; Liow T.-Y.; Song J.; Yu M.; Lo G. Q. Fabrication of Low Loss and High Speed Silicon Optical Modulator Using Doping Compensation Method. Opt. Express 2011, 19, 18029–18035. [DOI] [PubMed] [Google Scholar]
- Shannon C. E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- Li M.; Wang L.; Li X.; Xiao X.; Yu S. Silicon Intensity Mach–Zehnder Modulator for Single Lane 100 Gb/s Applications. Photonics Res. 2018, 6, 109–116. 10.1364/PRJ.6.000109. [DOI] [Google Scholar]
- Sun J.; Kumar R.; Sakib M.; Driscoll J. B.; Jayatilleka H.; Rong H. A 128 Gb/s PAM4 Silicon Microring Modulator with Integrated Thermo-Optic Resonance Tuning. J. Light. Technol. 2019, 37, 110–115. 10.1109/JLT.2018.2878327. [DOI] [Google Scholar]
- Harris N. C.; Ma Y.; Mower J.; Baehr-Jones T.; Englund D.; Hochberg M.; Galland C. Efficient, Compact and Low Loss Thermo-Optic Phase Shifter in Silicon. Opt. Express 2014, 22, 10487–10493. 10.1364/OE.22.010487. [DOI] [PubMed] [Google Scholar]
- Chen H.-W.; Peters J. D.; Bowers J. E. Forty Gb/s Hybrid Silicon Mach-Zehnder Modulator with Low Chirp. Opt. Express 2011, 19, 1455–1460. 10.1364/OE.19.001455. [DOI] [PubMed] [Google Scholar]
- Han J.-H.; Boeuf F.; Fujikata J.; Takahashi S.; Takagi S.; Takenaka M. Efficient Low-Loss InGaAsP/Si Hybrid MOS Optical Modulator. Nat. Photonics 2017, 11, 486–490. 10.1038/nphoton.2017.122. [DOI] [Google Scholar]
- Hiraki T.; Aihara T.; Fujii T.; Takeda K.; Tsuchizawa T.; Kakitsuka T.; Fukuda H.; Matsuo S.. Heterogeneously Integrated Mach-Zehnder Modulator Using Membrane InGaAsP Phase Shifter and Hydrogen-Free SiN Waveguide on Si Platform. Proceedings Of The 2018 European Conference On Optical Communication (ECOC); IEEE, 2018, 1–3.. [Google Scholar]
- Wang C.; Zhang M.; Chen X.; Bertrand M.; Shams-Ansari A.; Chandrasekhar S.; Winzer P. J.; Lončar M. Integrated Lithium Niobate Electro-Optic Modulators Operating at CMOS-Compatible Voltages. Nature 2018, 562, 101–104. 10.1038/s41586-018-0551-y. [DOI] [PubMed] [Google Scholar]
- Weigel P. O.; Zhao J.; Fang K.; Al-Rubaye H.; Trotter D.; Hood D.; Mudrick J.; Dallo C.; Pomerene A. T.; Starbuck A. L.; et al. Bonded Thin Film Lithium Niobate Modulator on a Silicon Photonics Platform Exceeding 100 GHz 3-dB Electrical Modulation Bandwidth. Opt. Express 2018, 26, 23728–23739. 10.1364/OE.26.023728. [DOI] [PubMed] [Google Scholar]
- He M.; Xu M.; Ren Y.; Jian J.; Ruan Z.; Xu Y.; Gao S.; Sun S.; Wen X.; Zhou L.; et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit/s and beyond. Nat. Photonics 2019, 13, 359–364. 10.1038/s41566-019-0378-6. [DOI] [Google Scholar]
- Li Y.; Lan T.; Yang D.; Bao J.; Xiang M.; Yang F.; Wang Z. High-Performance Mach-Zehnder Modulator Based on Thin-Film Lithium Niobate with Low Voltage-Length Product. ACS Omega 2023, 10, 9644–9651. 10.1021/acsomega.3c00310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomaschewski M.; Zenin V. A.; Fiedler S.; Wolff C.; Bozhevolnyi S. I. Plasmonic Lithium Niobate Mach Zehnder Modulators. Nano Lett. 2022, 16, 6471. 10.1021/acs.nanolett.2c00714. [DOI] [PubMed] [Google Scholar]
- Giambra M. A.; Sorianello V.; Miseikis V.; Marconi S.; Montanaro A.; Galli P.; Pezzini S.; Coletti C.; Romagnoli M. High-speed double layer graphene electro-absorption modulator on SOI waveguide. Opt. Express 2019, 27, 20145–20155. 10.1364/OE.27.020145. [DOI] [PubMed] [Google Scholar]
- Phare C. T.; Lee Y. D.; Cardenas J.; Lipson M. Graphene electro-optic modulators with 30 GHz bandwidth. Nat. Photonics 2015, 9, 511–514. 10.1038/nphoton.2015.122. [DOI] [Google Scholar]
- Agarwal H.; Terres B.; Orsini L.; Montanaro A.; Sorianello V.; Pantouvaki M.; Watanabe K.; Taniguchi T.; Thourhout D. V.; Romagnoli M.; Koppens F. H. L. 2D-3D integration of hexagonal boron nitride and a high-k dielectric for ultrafast graphene-based electro-absorption modulators. Nat. Commun. 2021, 12, 1070. 10.1038/s41467-021-20926-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorianello V.; Midrio M.; Contestabile G.; Asselberghs I.; Van Campenhout J.; Huyghebaert C.; Goykhman I.; Ott A. K.; Ferrari A. C.; Romagnoli M. Graphene-silicon phase modulators with gigahertz bandwidth. Nat. Photonics 2018, 12, 40–44. 10.1038/s41566-017-0071-6. [DOI] [Google Scholar]
- Thomson D.; Zilkie A.; Bowers J. E.; Komljenovic T.; Reed G. T.; Vivien L.; Marris-Morini D.; Cassan E.; Virot L.; Fedeli J.; Hartmann J. M.; Schmid J. H.; Xu D. X.; Boeuf F.; O’Brien P.; Mashanovich G. Z.; Nedeljkovic M. Roadmap on silicon photonics. J. Opt. 2016, 18, 073003. 10.1088/2040-8978/18/7/073003. [DOI] [Google Scholar]
- Xu Q.; Schmidt B.; Pradhan S.; Lipson M. Micrometre-scale silicon electro-optic modulator. Nature 2005, 435, 325–327. 10.1038/nature03569. [DOI] [PubMed] [Google Scholar]
- Liao L.; Samara-Rubio D.; Morse M.; Liu A.; Hodge D.; Rubin D.; Keil U. D.; Franck T. High speed silicon Mach-Zehnder modulator. Opt. Express 2005, 13, 3129–3135. 10.1364/OPEX.13.003129. [DOI] [PubMed] [Google Scholar]
- Thomson D. J.; Gardes F. Y.; Fedeli J.; Zlatanovic S.; Hu Y.; Kuo B. P. P.; Myslivets E.; Alic N.; Radic S.; Mashanovich G. Z.; et al. 50 Gbit/s Silicon Optical Modulator. IEEE Photonics Technol. Lett. 2012, 24, 234–236. 10.1109/LPT.2011.2177081. [DOI] [Google Scholar]
- Sinatkas G.; Christopoulos T.; Tsilipakos O.; Kriezis E. E. Electro-optic modulation in integrated photonics. J. Light. Technol. 2021, 130, 010901. 10.1063/5.0048712. [DOI] [Google Scholar]
- Soref R.; Bennett B. Electrooptical effects in silicon. IEEE J. Quantum Electron. 1987, 23, 123–129. 10.1109/JQE.1987.1073206. [DOI] [Google Scholar]
- Cocorullo G.; Rendina I. Thermo-optical modulation at 1.5 μm in silicon etalon. Electron. Lett. 1992, 28, 83–85. 10.1049/el:19920051. [DOI] [Google Scholar]
- De la Hidalga F.; Deen M. J.; Gutierrez E. A. Theoretical and experimental characterization of self-heating in silicon integrated devices operating at low temperatures. IEEE Trans. Electron Devices 2000, 47, 1098–1106. 10.1109/16.841246. [DOI] [Google Scholar]
- Masood A.; Pantouvaki M.; Lepage G.; Verheyen P.; Van Campenhout J.; Absil P.; Van Thourhout D.; Bogaerts W.. Comparison of heater architectures for thermal control of silicon photonic circuits. 10th International Conference On Group IV Photonics (GFP); IEEE, 2013, 83–84.. [Google Scholar]
- Hiraki T.; Aihara T.; Hasebe K.; Takeda K.; Fujii T.; Kakitsuka T.; Tsuchizawa T.; Fukuda H.; Matsuo S. Heterogeneously integrated III–V/Si MOS capacitor Mach–Zehnder modulator. Nat. Photonics 2017, 11, 482–485. 10.1038/nphoton.2017.120. [DOI] [Google Scholar]
- Numai T.Fundamentals of semiconductor lasers. In Fundamentals of Semiconductor lasers; Springer, 2015. [Google Scholar]
- Bennett B. R.; Soref R. A.; Alamo J. A. D. Carrier-induced change in refractive index of InP, GaAs and InGaAsP. IEEE J. Quantum Electron. 1990, 26, 113–122. 10.1109/3.44924. [DOI] [Google Scholar]
- Hsu W.-C.; Zhou B.; Wang A. X. MOS Capacitor-Driven Silicon Modulators: A Mini Review and Comparative Analysis of Modulation Efficiency and Optical Loss. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 3400211. 10.1109/JSTQE.2021.3127200. [DOI] [Google Scholar]
- Roelkens G.; Campenhout J. V.; Brouckaert J.; Thourhout D. V.; Baets R.; Romeo P. R.; Regreny P.; Kazmierczak A.; Seassal C.; Letartre X.; et al. III-V/Si photonics by die-to-wafer bonding. Mater. Today 2007, 10, 36–43. 10.1016/S1369-7021(07)70178-5. [DOI] [Google Scholar]
- Horowitz K. A. W.; Remo T.; Smith B.; Ptak A.. A Techno-Economic Analysis and Cost Reduction Roadmap for III-V Solar Cells; National Renewable Energy Laboratory, 2018. [Google Scholar]
- Ptak A.; Simon J.; Schulte K.. Bringing down the costs of III-V epitaxy; Compound Semiconductor, 2022. [Google Scholar]
- Wang C.; Zhang M.; Stern B.; Lipson M.; Loncar M. Nanophotonic lithium niobate electro-optic modulators. Opt. Express 2018, 26, 1547–1555. 10.1364/OE.26.001547. [DOI] [PubMed] [Google Scholar]
- Hu C.Modern semiconductor devices for integrated circuits; Pearson Education: Upper Saddle River, N.J.; London, 2010. [Google Scholar]
- Horowitz P.; Hill W.. The art of electronics; Cambridge University Press: Cambridge, 1980. [Google Scholar]
- Popovic Z.; Popovic B.. The skin effect. Introductory Electromagnetics; Prentice Hall, 1999. [Google Scholar]
- Meindl J. D.; Davis J. A.; Zarkesh-Ha P.; Patel C. S.; Martin K. P.; Kohl P. A. Interconnect opportunities for gigascale integration. IBM J. Res. Dev. 2002, 46, 245–263. 10.1147/rd.462.0245. [DOI] [Google Scholar]
- Bonaccorso F.; Sun Z.; Hasan T.; Ferrari A. C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. 10.1038/nphoton.2010.186. [DOI] [Google Scholar]
- Koppens F. H. L.; Mueller T.; Avouris P.; Ferrari A. C.; Vitiello M. S.; Polini M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 2014, 9, 780–793. 10.1038/nnano.2014.215. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Bonaccorso F.; Fal’ko V.; Novoselov K. S.; Roche S.; Boggild P.; Borini S.; Koppens F. H.; Palermo V.; Pugno N.; et al. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7, 4598–4810. 10.1039/C4NR01600A. [DOI] [PubMed] [Google Scholar]
- Romagnoli M.; Sorianello V.; Midrio M.; Koppens F. H.; Huyghebaert C.; Neumaier D.; Galli P.; Templ W.; D’Errico A.; Ferrari A. C. Graphene-based integrated photonics for next-generation datacom and telecom. Nat. Rev. Mater. 2018, 3, 392–414. 10.1038/s41578-018-0040-9. [DOI] [Google Scholar]
- Purdie D. G.; Pugno N. M.; Taniguchi T.; Watanabe K.; Ferrari A. C.; Lombardo A. Cleaning interfaces in layered materials heterostructures. Nat. Commun. 2018, 9, 5387. 10.1038/s41467-018-07558-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazio D. D.; Purdie D. G.; Ott A. K.; Braeuninger-Weimer P.; Khodkov T.; Goossens S.; Taniguchi T.; Watanabe K.; Livreri P.; Koppens F. H. L.; et al. High-Mobility, Wet-Transferred Graphene Grown by Chemical Vapour Deposition. ACS Nano 2019, 13, 8926–8935. 10.1021/acsnano.9b02621. [DOI] [PubMed] [Google Scholar]
- Wang F.; Zhang Y.; Tian C.; Girit C.; Zettl A.; Crommie M.; Shen Y. R. Gate-variable optical transitions in graphene. Science 2008, 320, 206–209. 10.1126/science.1152793. [DOI] [PubMed] [Google Scholar]
- Li Z. Q.; Henriksen E. A.; Jiang Z.; Hao Z.; Martin M. C.; Kim P.; Stormer H. L.; Basov D. N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. 10.1038/nphys989. [DOI] [Google Scholar]
- Nair R. R.; Blake P.; Grigorenko A. N.; Novoselov K. S.; Booth T. J.; Stauber T.; Peres N. M. R.; Geim A. K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. 10.1126/science.1156965. [DOI] [PubMed] [Google Scholar]
- Pisana S.; Lazzeri M.; Casiraghi C.; Novoselov K. S.; Geim A. K.; Ferrari A. C.; Mauri F. Breakdown of the adiabatic Born–Oppenheimer approximation in graphene. Nat. Mater. 2007, 6, 198–201. 10.1038/nmat1846. [DOI] [PubMed] [Google Scholar]
- Sorianello V.; Midrio M.; Romagnoli M. Design optimization of single and double layer Graphene phase modulators in SOI. Opt. Express 2015, 23, 6478–6490. 10.1364/OE.23.006478. [DOI] [PubMed] [Google Scholar]
- Bonaccorso F.; Lombardo A.; Hasan T.; Sun Z.; Colombo L.; Ferrari A. C. Production and processing of graphene and 2d crystals. Mater. Today 2012, 15, 564–589. 10.1016/S1369-7021(13)70014-2. [DOI] [Google Scholar]
- Backes C.; Abdelkader A. M.; Alonso C.; Andrieux-Ledier A.; Arenal R.; Azpeitia J.; Balakrishnan N.; Banszerus L.; Barjon J.; Bartali R.; et al. Production and processing of graphene and related materials. 2D Mater. 2020, 7, 022001. 10.1088/2053-1583/ab1e0a. [DOI] [Google Scholar]
- Bae S.; Kim H.; Lee Y.; Xu X.; Park J.; Zheng Y.; Balakrishnan J.; Lei T.; Kim H. R.; Song Y. I.; et al. Roll-to-roll production of 30-in. graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5, 574–578. 10.1038/nnano.2010.132. [DOI] [PubMed] [Google Scholar]
- Miseikis V.; Bianco F.; David J.; Gemmi M.; Pellegrini V.; Romagnoli M.; Coletti C. Deterministic patterned growth of high-mobility large-crystal graphene: A path towards wafer scale integration. 2D Mater. 2017, 4, 021004. 10.1088/2053-1583/aa5481. [DOI] [Google Scholar]
- Muench J. E.; Ruocco A.; Giambra M. A.; Miseikis V.; Zhang D.; Wang J.; Watson H. F.; Park G. C.; Akhavan S.; Sorianello V.; et al. Waveguide-Integrated, Plasmonic Enhanced Graphene Photodetectors. Nano Lett. 2019, 19, 7632–7644. 10.1021/acs.nanolett.9b02238. [DOI] [PubMed] [Google Scholar]
- Wu C.; Brems S.; Yudistira D.; Cott D.; Milenin A.; Vandersmissen K.; Maestre A.; Centeno A.; Zurutuza A.; Campenhout J. V.; et al. Wafer-Scale Integration of Single Layer Graphene Electro-Absorption Modulators in a 300 mm CMOS Pilot Line. Lasers And Photonics Rev. 2023, 17, 2200789. 10.1002/lpor.202200789. [DOI] [Google Scholar]
- Liu M.; Yin X.; Zhang X. Double-Layer Graphene Optical Modulator. Nano Lett. 2012, 12, 1482–1485. 10.1021/nl204202k. [DOI] [PubMed] [Google Scholar]
- Mohsin M.; Neumaier D.; Schall D.; Otto M.; Matheisen C.; Giesecke A. L.; Sagade A. A.; Kurz H. Experimental verification of electro-refractive phase modulation in graphene. Sci. Rep. 2015, 5, 10967. 10.1038/srep10967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dalir H.; Xia Y.; Wang Y.; Zhang X. Athermal Broadband Graphene Optical Modulator With 35 GHz Speed. ACS Photonics 2016, 3, 1564–1568. 10.1021/acsphotonics.6b00398. [DOI] [Google Scholar]
- Liu M.; Yin X.; Ulin-Avila E.; Geng B.; Zentgraf T.; Ju L.; Wang F.; Zhang X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. 10.1038/nature10067. [DOI] [PubMed] [Google Scholar]
- Sorianello V.; De Angelis G.; Cassese T.; Midrio M.; Romagnoli M.; Mohsin M.; Otto M.; Neumaier D.; Asselberghs I.; Van Campenhout J.; Huyghebaert C. Complex effective index in graphene-silicon waveguides. Opt. Express 2016, 24, 29984–29993. 10.1364/OE.24.029984. [DOI] [PubMed] [Google Scholar]
- Zhu S.; Fang Q.; Yu M. B.; Lo G. Q.; Kwong D. L. Propagation losses in undoped and n-doped polycrystalline silicon wire waveguides. Opt. Express 2009, 17, 20891–20899. 10.1364/OE.17.020891. [DOI] [PubMed] [Google Scholar]
- Canali C.; Jacoboni C.; Nava F.; Ottaviani G.; Alberigi-Quaranta A. Electron drift velocity in silicon. Phys. Rev. B 1975, 12, 2265–2284. 10.1103/PhysRevB.12.2265. [DOI] [Google Scholar]
- Kubo R.; Yokota M.; Nakajima S. Statistical-Mechanical Theory of Irreversible Processes. II. Response to Thermal Disturbance. J. Phys. Soc. Jpn. 1957, 12, 1203–1211. 10.1143/JPSJ.12.1203. [DOI] [Google Scholar]
- Das Sarma S.; Adam S.; Hwang E. H.; Rossi E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407–470. 10.1103/RevModPhys.83.407. [DOI] [Google Scholar]
- Kotov V. N.; Uchoa B.; Pereira V. M.; Guinea F.; Neto A. H. C. Electron-Electron Interactions in Graphene: Current Status and Perspectives. Rev. Mod. Phys. 2012, 84, 1067–1125. 10.1103/RevModPhys.84.1067. [DOI] [Google Scholar]
- Chang Y.-C.; Liu C.-H.; Liu C.; Zhong Z.; Norris T. B. Extracting the complex optical conductivity of mono- and bilayer graphene by ellipsometry. Appl. Phys. Lett. 2014, 104, 261909. 10.1063/1.4887364. [DOI] [Google Scholar]
- Kuzmenko A. B.; Van Heumen E.; Carbone F.; van der Marel D. Universal Optical Conductance of Graphite. Phys. Rev. Lett. 2008, 100, 117401. 10.1103/PhysRevLett.100.117401. [DOI] [PubMed] [Google Scholar]
- Hanson G. W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. 10.1063/1.2891452. [DOI] [Google Scholar]
- Falkovsky L. A.; Pershoguba S. S. Optical far-infrared properties of a graphene monolayer and multilayer. Phys. Rev. B 2007, 76, 153410. 10.1103/PhysRevB.76.153410. [DOI] [Google Scholar]
- Kittel C.Introduction to solid state physics.; John Wiley & Sons: New York, 1996. [Google Scholar]
- Das A.; Pisana S.; Chakraborty B.; Piscanec S.; Saha S. K.; Waghmare U. V.; Novoselov K. S.; Krishnamurthy H. R.; Geim A. K.; Ferrari A. C.; et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008, 3, 210–215. 10.1038/nnano.2008.67. [DOI] [PubMed] [Google Scholar]
- Mak K.; Sfeir M.; Wu Y.; Lui C.; Misewich J.; Heinz T. Measurement of the Optical Conductivity of Graphene. Phys. Rev. Lett. 2008, 101, 196405. 10.1103/PhysRevLett.101.196405. [DOI] [PubMed] [Google Scholar]
- Gosciniak J.; Tan D. T. H. Theoretical investigation of graphene-based photonic modulators. Sci. Rep 2013, 3, 1897. 10.1038/srep01897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Z.; Brown T. G. Full-vectorial finite-difference analysis of microstructured optical fibers. Opt. Express 2009, 17, 853–864. 10.1364/OE.10.000853. [DOI] [PubMed] [Google Scholar]
- Bienstman P.; Baets R. Optical modelling of photonic crystals and VCSELs using eigenmode expansion and perfectly matched layers. Opt. Mater. Express 2001, 33, 327–341. 10.1023/A:1010882531238. [DOI] [Google Scholar]
- Luryi S. Quantum capacitance devices. Appl. Phys. Lett. 1988, 52, 501–503. 10.1063/1.99649. [DOI] [Google Scholar]
- Xia J.; Chen F.; Li J.; Tao N. Measurement of the quantum capacitance of graphene. Nat. Nanotechnol. 2009, 4, 505–514. 10.1038/nnano.2009.177. [DOI] [PubMed] [Google Scholar]
- Das A.; Chakraborty B.; Piscanec S.; Pisana S.; Sood A. K.; Ferrari A. C. Phonon renormalization in doped bilayer graphene. Phys. Rev. Lett. B 2009, 79, 155417. 10.1103/PhysRevB.79.155417. [DOI] [Google Scholar]
- Hwang E. H.; Adam S.; Sarma S. D. Carrier Transport in Two-Dimensional Graphene Layers. Phys. Rev. Lett. 2007, 98, 186806. 10.1103/PhysRevLett.98.186806. [DOI] [PubMed] [Google Scholar]
- Absil P. P.; Verheyen P.; De Heyn P.; Pantouvaki M.; Lepage G.; De Coster J.; Van Campenhout J. Silicon photonics integrated circuits: a manufacturing platform for high density, low power optical I/O’s. Opt. Express 2015, 23, 9369–9378. 10.1364/OE.23.009369. [DOI] [PubMed] [Google Scholar]
- Li X.; Cai W.; An J.; Kim S.; Nah J.; Yang D.; Piner R.; Velamakanni A.; Jung I.; Tutuc E.; et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 2009, 324, 1312–1316. 10.1126/science.1171245. [DOI] [PubMed] [Google Scholar]
- Lagatsky A. A.; Sun Z.; Kulmala T. S.; Sundaram R. S.; Milana S.; Torrisi F.; Antipov O. L.; Lee Y.; Ahn J. H.; Brown C.; et al. 2μm solid-state laser mode-locked by single-layer graphene. Appl. Phys. Lett. 2013, 102, 013113. 10.1063/1.4773990. [DOI] [Google Scholar]
- Ferrari A. C.; Meyer J. C.; Scardaci V.; Casiraghi C.; Lazzeri M.; Mauri F.; Piscanec S.; Jiang D.; Novoselov K. S.; Roth S.; et al. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 97, 187401. 10.1103/PhysRevLett.97.187401. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Basko D. M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. 10.1038/nnano.2013.46. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Robertson J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 2000, 61, 14095. 10.1103/PhysRevB.61.14095. [DOI] [Google Scholar]
- Cançado L. G.; Jorio A.; Ferreira E. H.; Stavale F.; Achete C. A.; Capaz R. B.; Moutinho M. V.; Lombardo A.; Kulmala T. S.; Ferrari A. C. Quantifying defects in graphene via Raman spectroscopy at different excitation energies. Nano Lett. 2011, 11, 3190–3196. 10.1021/nl201432g. [DOI] [PubMed] [Google Scholar]
- Basko D. M.; Piscanec S.; Ferrari A. C. Electron-electron interactions and doping dependence of the two-phonon Raman intensity in graphene. Phys. Rev. B 2009, 80, 165413. 10.1103/PhysRevB.80.165413. [DOI] [Google Scholar]
- Bruna M.; Ott A. K.; Ijäs M.; Yoon D.; Sassi U.; Ferrari A. C. Doping Dependence of the Raman Spectrum of Defected Graphene. ACS Nano 2014, 8, 7432–7441. 10.1021/nn502676g. [DOI] [PubMed] [Google Scholar]
- Shaygan M.; Otto M.; Sagade A. A.; Chavarin C. A.; Bacher G.; Mertin W.; Neumaier D. Low Resistive Edge Contacts to CVD-Grown Graphene Using a CMOS Compatible Metal. Ann. Phys. 2017, 529, 1600410. 10.1002/andp.201600410. [DOI] [Google Scholar]
- Mohiuddin T. M. G.; Lombardo A.; Nair R. R.; Bonetti A.; Savini G.; Jalil R.; Bonini N.; Basko D. M.; Galiotis C.; Nicola M. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Gruneisen parametrs, and sample orientation. Phys. Rev. B 2009, 79, 205433. 10.1103/PhysRevB.79.205433. [DOI] [Google Scholar]
- Yoon D.; Son Y.-W.; Cheong H. Strain-Dependent Splitting of the Double-Resonance Raman Scattering Band in Graphene. Phys. Rev. Lett. 2011, 106, 155502. 10.1103/PhysRevLett.106.155502. [DOI] [PubMed] [Google Scholar]
- Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–675. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- Mears R.; Reekie L.; Jauncey I.; Payne D. Low-noise erbium-doped fibre amplifier operating at 1.54m. Electron. Lett. 1987, 23, 1026–1028. 10.1049/el:19870719. [DOI] [Google Scholar]
- Newport InGaAs Photodetector Website. https://www.newport.com/f/40-ghz-and-45-ghz-.
- Uehara S. Calibration of optical modulator frequency response with application to signal level control. Appl. Opt. 1978, 17, 68–71. 10.1364/AO.17.000068. [DOI] [PubMed] [Google Scholar]
- Urban F.; Lupina G.; Grillo A.; Martucciello N.; Di Bartolomeo A. Contact resistance and mobility in back-gate graphene transistors. Nano Express 2020, 1, 010001. 10.1088/2632-959X/ab7055. [DOI] [Google Scholar]
- Madsen C. K.; Zhao J. H.. Optical filter design and analysis: A signal processing approach; John Wiley & Sons: New York, Chichester, 1999. [Google Scholar]
- Tan Y.-W.; Zhang Y.; Bolotin K.; Zhao Y.; Adam S.; Hwang E. H.; Sarma S. D.; Stormer H. L.; Kim P. Measurement of Scattering Rate and Minimum Conductivity in Graphene. Phys. Rev. Lett. 2007, 99, 246803. 10.1103/PhysRevLett.99.246803. [DOI] [PubMed] [Google Scholar]
- Chen J. H.; Jang C.; Adam S.; Fuhrer M. S.; Williams E. D.; Ishigami M. Charged-impurity scattering in graphene. Nat. Phys. 2008, 4, 377–381. 10.1038/nphys935. [DOI] [Google Scholar]
- Aničić R.; Mišković Z. L. Effects of the structure of charged impurities and dielectric environment on conductivity of graphene. Phys. Rev. B 2013, 88, 205412. 10.1103/PhysRevB.88.205412. [DOI] [Google Scholar]
- Dong P.; Chen L.; Chen Y. K. High-speed low-voltage single-drive push-pull silicon Mach-Zehnder modulators. Opt. Express 2012, 20, 6163–6169. 10.1364/OE.20.006163. [DOI] [PubMed] [Google Scholar]
- Zhu Y.; Zhang J.; Cheng T.; Tang J.; Duan H.; Hu Z.; Shao J.; Wang S.; Wei M.; Wu H.; et al. Controlled Growth of Single-Crystal Graphene Wafers on Twin-Boundary-Free Cu(111) Substrates. Adv. Mater. 2024, 36 (17), 2308802. 10.1002/adma.202308802. [DOI] [PubMed] [Google Scholar]
- Jia-Ming L.Principles of photonics; Cambridge University Press, 2016. [Google Scholar]
- Lumerical Inc Lumerical. https://www.lumerical.com/. accessed 1 August 2024.