Abstract
Two-dimensional (2D) ion crystals may represent a promising path to scale up qubit numbers for ion trap quantum information processing. However, to realize universal quantum computing in this system, individually addressed high-fidelity two-qubit entangling gates still remain challenging due to the inevitable micromotion of ions in a 2D crystal as well as the technical difficulty in 2D addressing. Here we demonstrate two-qubit entangling gates between any ion pairs in a 2D crystal of four ions. We use symmetrically placed crossed acousto-optic deflectors (AODs) to drive Raman transitions and achieve an addressing crosstalk error below 0.1%. We design and demonstrate a gate sequence by alternatingly addressing two target ions, making it compatible with any single-ion addressing techniques without crosstalk from multiple addressing beams. We further examine the gate performance versus the micromotion amplitude of the ions and show that its effect can be compensated by a recalibration of the laser intensity without degrading the gate fidelity. Our work paves the way for ion trap quantum computing with hundreds to thousands of qubits on a 2D ion crystal.
Subject terms: Quantum information, Qubits
Quantum gates in 2D ion crystals are more challenging than in 1D. Here, the authors use their 2D ion trap platform and acousto-optical deflectors to demonstrate a 2-qubit gate that can stand the ion micromotion in such configuration.
Introduction
Quantum computation has attracted wide research interest because of its potential computational power beyond the framework of classical computers1. To date, various physical platforms have demonstrated elementary quantum operations whose fidelities are above the threshold of fault-tolerant quantum computing2–8. However, to obtain a large-scale error-corrected universal quantum computer and to solve practical problems like factoring, the currently available qubit number of tens to hundreds2,6,9–11 still needs to be improved by several orders of magnitude12, which remains an outstanding challenge to the community.
As one of the leading physical platforms for quantum information processing, trapped ions are remarkable for their high-fidelity quantum operations and long-range entangling gates13. A single-qubit gate fidelity above 99.9999%14, a two-qubit gate fidelity above 99.9%4,5,15, and a state-preparation-and-measurement fidelity above 99.99%16 have been reported. However, the number of qubits in the commonly used one-dimensional (1D) configuration of ion crystals is seriously limited17–19. To avoid the buckling of the ions into a zigzag pattern, the axial trap frequency needs to be decreased as the ion number increases, making the system sensitive to the low-frequency electric field noise. To further scale up the qubit number, one promising scheme is the quantum charge-coupled device (QCCD) architecture where ions are physically shuttled into small crystals in separated regions for different tasks like storage, quantum gates and measurements10,17,20. However, currently this scheme is limited by the relatively slow transport speed of the ions and the follow-up cooling operations, which take up more than 98% of the time budget10. On the other hand, an ion-photon quantum network can connect up individual quantum computing modules21–23 and is compatible with the 1D ion crystals or the QCCD architectures. However, its performance is restricted by the relatively low efficiency for ion-photon entanglement generation and ion-ion entanglement connection via Bell measurement of photons24. Therefore it is still desirable to push up the qubit number in each module to reduce the communication overhead.
Two-dimensional (2D) ion crystals have long been used for quantum simulation in Penning trap25,26 with individual addressing scheme also being proposed27. Recently, 2D ion crystals have also been utilized to largely extend the ionic qubit number in a single Paul trap28–34. In particular, quantum simulation with up to 300 ions has been demonstrated34. Despite the site-resolved single-shot measurement capability, previous experiments are still restricted to global quantum manipulations, while individually addressed single-qubit and two-qubit quantum gates have not yet been realized. Fundamentally, the inevitable micromotion of ions in a 2D crystal seems to affect the gate performance, although theoretical works already show that the micromotion is a coherent process and can in principle be included into the gate design, still allowing high gate fidelity35–39. Technically, individual addressing in 2D is also more complicated than 1D40–44. For example, although crossed AODs can address a rectangular array by generating multiple beams within a single row or a single column40, it struggles to address two ions along the diagonal without creating undesired light spots on the other two corners.
Here we solve these problems by developing a two-qubit gate sequence that addresses only one ion at a time. We demonstrate a crosstalk below 0.1% by symmetrically placed crossed AODs, and realize two-qubit entangling gates between any ion pairs in a 2D crystal. By pushing an ion pair away from the RF null axis of the trap, we adjust the micromotion amplitude and experimentally show that it does not affect the gate fidelity up to a recalibration of the laser intensity. Combined with gate sequences with more degrees of freedom, our work can be readily applied to larger 2D ion crystals, thus paves the way toward ion trap quantum computing with hundreds to thousands of qubits in a single quantum computation module.
Results
Experimental setup
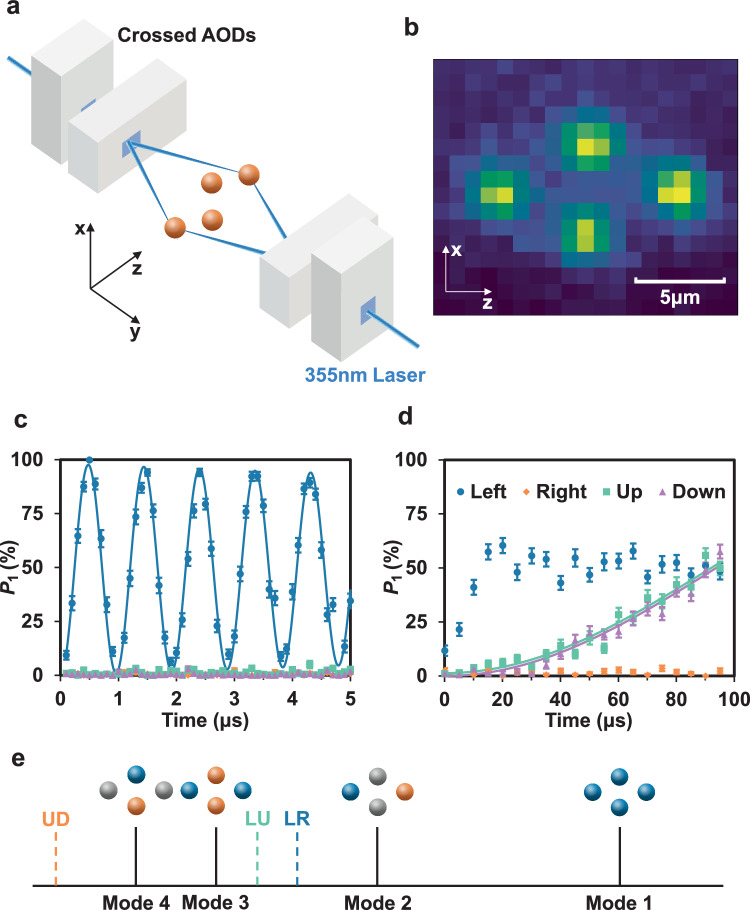
Our experimental setup is sketched in Fig. 1a. We design a special configuration of the blade trap, as described in Methods, to obtain a 2D crystal of 171Yb+ ions perpendicular to the imaging direction while allowing wide optical access. A DC bias voltage is applied on both RF electrodes to split the radial trap frequency into ωx = 2π × 0.803 MHz and ωy = 2π × 2.284 MHz. We further use DC electrodes for the axial trapping ωz = 2π × 0.553 MHz and obtain a 2D crystal whose major axis is oriented in the z direction as shown in Fig. 1b. In the following we label our four trapped ions in a 2D crystal by left (L), right (R), up (U) and down (D). Due to the overlap between the images of adjacent ions and the low photon collection efficiency, there exists considerable crosstalk error in the single-shot measurement of the four qubits encoded in and under 370 nm detection laser. In the future, this can be improved by electron shelving to the D5/2 and F7/2 levels45,46, but in this experiment for the purpose of calibrating individual addressing and two-qubit gate errors, it suffices to recover the population in the 24 = 16 computational basis states by the maximum likelihood method. More details can be found in Methods.
Fig. 1. Experimental setup and 2D individual addressing.
a We address a 2D ion crystal in the xz plane by two pairs of symmetrically placed crossed AODs. By tuning the driving frequency of the AODs, the incoming 355 nm laser can be steered in the x or z directions to form a Raman transition on a target ion. By applying two frequencies to an AOD, we can generate addressing beams for two target ions simultaneously, e.g., along the z direction. (Created for this article by Y.-H. H. and Y.-J. Y., and since published in ref. 59). b The image of the four-ion crystal on an EMCCD camera. The z axis is chosen to be the micromotion-free axial direction of the trap. Below we label the four ions by left, right, up and down according to this image. c Rabi oscillation of the four ions when addressing the left ion, where P1 is the probability to find the ions in the bright state . Error bars represent one standard deviation. d Similar plot as (c) for longer evolution time. Crosstalk infidelity can be estimated by comparing the Rabi rates of different ions. Note that the oscillation for the left ion is not visible here due to the insufficient time points. e Schematic of the four transverse (drumhead) modes with frequencies ωk = 2π × (2.284, 2.216, 2.167, 2.138) MHz (k = 1, 2, 3, 4). The blue, gray and orange colors of the ions represent the positive, zero and negative mode amplitudes, respectively. The vertical dashed lines indicate the laser detuning for two-qubit gates between the left-right (LR), up-down (UD) and left-up (LU) ion pairs.
We use two pairs of symmetrically placed crossed AODs for individual addressing of the 355 nm Raman laser beams40. By tuning the driving frequencies on the horizontal or vertical AODs, the addressing beam can be scanned along the z or x directions, respectively. The objectives for the two addressing beams have the same focal length so that the two pairs of crossed AODs have equal driving frequencies when addressing the same target ion. In this way, the frequency shift introduced by the AODs can be canceled in the Raman transition40. Also note that previously the crossed AODs have been used for 1D individual addressing along the diagonal direction where the frequency shift due to the + 1 diffraction order of the first AOD can be compensated by that of the − 1 diffraction order of the second one47,48. Each Raman beam has a waist radius (where the intensity drops to 1/e2) of about 1.5 μm as compared with the distance between adjacent ions of about 5 μm. To estimate the crosstalk for individual addressing, we drive a resonant Raman transition between and on one target ion, and measure the Rabi oscillation of all the ions. An example is shown in Fig. 1c, d for the addressing beam on the left ion. By fitting the Rabi frequency of ΩL = 2π × 1.04 MHz for the left ion, and ΩU = ΩD = 2π × 2.7 kHz for the up and down ions (the Rabi rate for the right ion is even smaller due to its larger distance), we estimate the crosstalk infidelity for a single-qubit π pulse to be . Similarly, we measure the crosstalk for other target ions as shown in Supplementary Fig. 3 and obtain a maximal crosstalk infidelity of 0.08%.
The four transverse (drumhead) phonon modes of the four-ion crystal are illustrated in Fig. 1e. Mediated by these phonon modes, two-qubit entangling gates between any ion pair, say, LR, UD or LU, can be realized by spin-dependent forces via, e.g., a phase-modulated gate sequence49.
Individually addressed two-qubit gates
For universal quantum computing, we want two-qubit entangling gates between all ion pairs, or at least a connected graph of them. For our four-ion crystal, this set includes a horizontal pair (LR), a vertical pair (UD), and four diagonal pairs (LU, LD, RU and RD). Here we demonstrate the entangling gates for the LR, UD and LU pairs, and expect similar performance for other diagonal pairs by symmetry.
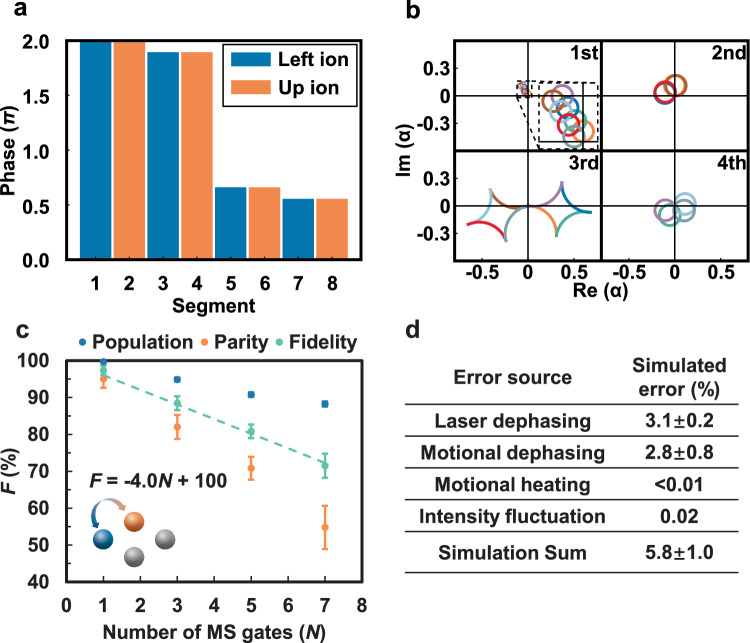
With the crossed AODs, the horizontal or the vertical pair can be easily addressed by applying two frequency components to the horizontal or the vertical AODs, respectively. Then we can use bichromatic 355 nm Raman laser to generate spin-dependent forces on the target ions50 and use a phase-modulated gate sequence to disentangle the spin and the motional states at the end of the gate49. For the horizontal pair, as shown in Fig. 1e, the fourth phonon mode has zero mode coefficient and thus can be ignored in the gate design. We set the Raman laser detuning μ = (ω2 + ω3)/2 in the middle of Mode 2 and Mode 3 such that after each segment of t = 4π/(ω2 − ω3) (one loop in the phase space) they will be disentangled simultaneously. We further choose the phase shift between two segments to decouple the center-of-mass (COM) mode and obtain the total gate time T = 2t = 81.6 μs. Finally, we scale the laser intensity for the accumulated two-spin phase to give us a maximally entangled two-qubit gate. As shown in Fig. 2a, b, we obtain a population of 99.6(1)% in and , and a parity contrast of 98(2)%, thus a Bell state fidelity of 99(1)% for the LR pair50. As we show in Fig. 2c, the error mainly comes from the laser dephasing time of 4 ms due to the optical phase fluctuation between the two Raman beams, and the motional dephasing time of 3 ms. However, note that these theoretical analyses are based on a white-noise model, which seems to systematically over-estimate the gate error by about 50% as the actual noise can be dominated by the low-frequency part. More details can be found in Methods.
Fig. 2. Entangling gates between ion pairs in the same row or the same column.
a Population for the LR ion pair after an entangling gate. b Parity oscillation for the LR ion pair after an entangling gate. c Theoretical estimation of gate errors for the LR and the UD ion pairs. The laser dephasing, motional dephasing and motional heating effects are modeled by Lindblad operators. The intensity fluctuation is described by a shot-to-shot variation. d Experimentally measured Bell-state fidelity for the LR ion pair vs. the number of entangling gates. The blue and the orange data points represent the population and parity, respectively, while the fidelity is their average as the green dots. By fitting the slope of the fidelity, we extract a gate infidelity of about 1.4(2)%. e Similar plot for the UD ion pair with an extracted gate infidelity of about 1.6(1)%. All the error bars represent one standard deviation.
Similarly, we can address the UD ion pair by two frequency components on the vertical AODs. These two ions do not participate in the second mode, and we set the Raman laser detuning as μ = 2ω4 − ω3 such that after each segment of t = 2π/(ω3 − ω4), one loop in the phase space will be traversed by the fourth mode while two by the third mode. Again we use two segments with an adjustable phase shift to disentangle the COM mode. At the total gate time T = 2t = 69.0 μs, we obtain a Bell state fidelity of 98(2)%. The theoretical fidelity is lower than that of the LR pair because of a stronger laser intensity and thus larger motional excitations during the gate sequence, leaving the gate more sensitive to the motional dephasing error as shown in Fig. 2c.
In Fig. 2d, e, we repeat the two-qubit gates for an odd number of times and examine the decay of the Bell state fidelity vs. the repetition number. Assuming a dominant incoherent error, this can be used to separate the gate infidelity from the state-preparation-and-measurement (SPAM) error42,51, although in our case the detection error is already corrected reasonably well and indeed we fit an intercept close to 100%. Nevertheless, it still allows us to reduce the statistical uncertainty and we fit the gate infidelities to be 1.4(2)% and 1.6(1)%, respectively, for LR and UD pairs.
To address the LU ion pair by the crossed AODs is more complicated. If we apply two frequency components to both the horizontal and the vertical AODs, four light spots in a rectangular pattern will be generated. It not only decreases the laser intensity on the target ions, but also causes stronger crosstalk on the other ions due to the undesired light spots. To circumvent this problem, we develop an alternating gate sequence such that at any time only a single ion will be addressed. Note that although we demonstrate this scheme on crossed AODs, it is also compatible with other 2D addressing techniques.
Similar to the commonly used Molmer–Sorensen gate with amplitude, phase or frequency modulation49,52,53, our alternating gate sequence also aims to disentangle the spin and the phonon modes while accumulating a desired two-qubit phase for maximal entanglement. Note that the two-qubit phase comes from the commutation relation between a new displacement in the phase space and an accumulative one (see Methods), and does not require simultaneous addressing of both ions. Specifically, for the LU ion pair we design a phase modulation sequence as shown in Fig. 3a with a Raman laser detuning μ = (ω2 + ω4)/2 in the middle of Mode 2 and Mode 4, and a segment duration t = 4π/(ω2 − ω4). Note that these two modes have participation of only one ion from the desired LU ion pair, hence do not contribute to the two-qubit phase. Therefore we use the above elementary segment to disentangle them from the spin states trivially. The rest two phonon modes can be disentangled by four phase-modulation segments49, and we apply such a sequence alternatingly on the two target ions, obtaining the sequence in Fig. 3a. We set a separation Δt = 2 μs between adjacent segments to avoid crosstalk when switching the addressing beam. This gives us a total gate time of T = 8t + 7Δt = 219.1 μs. The corresponding phase space trajectories for the four phonon modes from the initial spin state (an eigenstate of the laser-induced spin-dependent force, see Methods) is shown in Fig. 3b, with different segments indicated by different colors. As designed, all these trajectories close at the end of the gate. Then we repeat the entangling gate for an odd number of times in Fig. 3c and fit a gate infidelity of 4.0(3)%, which is again dominated by the laser dephasing and motional dephasing effects as shown in Fig. 3d.
Fig. 3. Entangling gate between a diagonal ion pair.
a Phase modulation sequence for the LU ion pair. We alternatingly apply the driving laser on the two target ions, indicated by the color of the bars, with a fixed laser detuning μLU = (ω2 + ω4)/2. Each segment takes time t = 4π/(ω2 − ω4) with the laser phase given by the height of the bars. We set a separation Δt = 2 μs between adjacent segments to turn the driving laser off and on, so as to avoid crosstalk during the switching. b Theoretical phase space trajectories for the four phonon modes when the spin state is . Different segments are indicated by different colors. c Similar plot as Fig. 2d, e for the LU ion pair. A gate infidelity of 4.0(3)% is fitted. d Similar plot as Fig. 2c for theoretically simulated gate errors. All the error bars represent one standard deviation.
Note that the above construction of gate sequences to disentangle all the phonon modes exactly can become inefficient as the ion number increases49. As we describe in Supplementary Note 1, we can also use a moderate number of segments to decouple the spin and the phonon modes approximately while still achieving high gate fidelity.
Effects of micromotion
In our four-ion crystal, the LR pair locates on the RF null axis, while the UD pair has nonzero excess micromotion proportional to the deviation from the RF null. From the above results, we see that the entangling gates on these two ion pairs have similar infidelities and that their difference is mainly caused by the different gate time and phonon excitations rather than the existence of micromotion. This suggests that micromotion of ions in a 2D crystal is not a limiting factor for the gate performance.
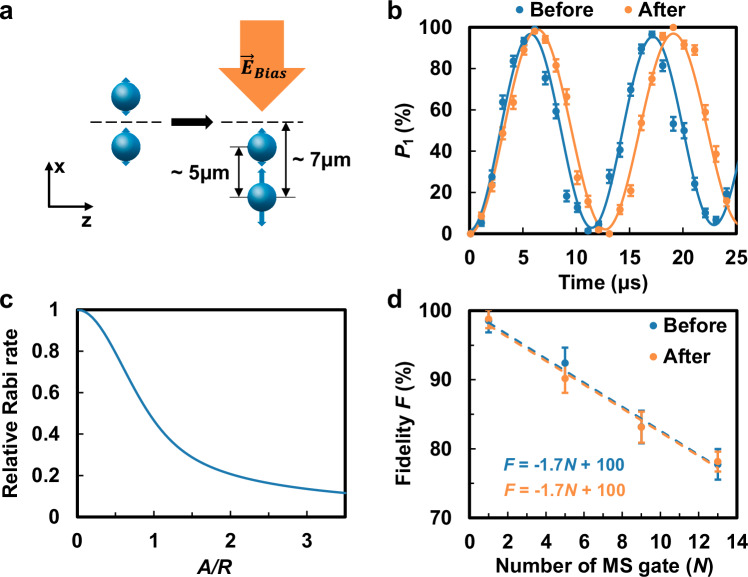
We further examine the influence of micromotion in Fig. 4 using a two-ion crystal aligned in the x direction. We apply a bias voltage on one DC and one RF electrode to create a bias electric field along the x direction and push the ion pair away from the RF null axis. Theoretically, the micromotion amplitude is given by A = qx/2 where x is the coordinate of the concerned ion and q = 0.12 is the Mathieu parameter in that direction54. As the micromotion amplitude becomes comparable to the radius R = 1.5 μm of the addressing beams, we expect a reduction in the effective laser intensity felt by the ions. This can be seen from Fig. 4b where we plot the Raman Rabi oscillation of the lower ion before (blue) and after (orange) the displacement under the same laser intensity. We fit the corresponding Rabi frequencies and get their ratio Ω2/Ω1 = 0.90. If we assume a Gaussian profile of the addressing beams, we can theoretically compute the relative Rabi rate (Fig. 4c) where I0(x) is the modified Bessel function of the first kind. Here we average over an RF period without worrying about its initial phase because the RF frequency ωrf = 2π × 37 MHz is much higher than any other timescales in this experiment. This calculation predicts a Rabi rate ratio of 0.935. Small deviation between theoretical and experimental results may come from the non-Gaussian distribution of the laser intensity.
Fig. 4. Entangling gates under micromotion.
a We orient an ion pair along the x axis with a separation of about 5 μm (read from the image on the CCD camera as 0.88 μm/pixel). Then we push the ion pair away from the micromotion-free z axis by a bias electric field. The relative micromotion amplitudes of the two ions are indicated by the blue arrows, which are not to scale with the ion spacing or their displacements. b Rabi oscillations of the lower ion under a Raman laser with the same intensity before (blue) and after (orange) the displacement. c Theoretical relative Rabi rate r vs. the micromotion amplitude A in the unit of the laser waist radius R = 1.5 μm. d Bell-state fidelity vs. the number of entangling gates for the ion pairs before (blue) and after (orange) the displacement. We fit both gate infidelities to be 1.7(1)%. All the error bars represent one standard deviation.
We further perform two-qubit gates on the ion pair before and after the displacement. We set the laser detuning to the middle of the two phonon modes and evolve both modes by four loops in the phase space for a gate time of about 100 μs. As shown in Fig. 4d, after calibrating the laser intensity, we get almost the same gate performance with small (blue) or large (orange) excess micromotion. Also note that due to the different micromotion amplitudes of the two ions, their effective Rabi rates will differ under the same laser intensity. Ideally, a two-qubit phase can still be obtained which is proportional to the product of the two Rabi frequencies, but it may increase the spontaneous emission error from the excited states. Therefore, here we calibrate the intensities of the two addressing beams to ensure the same effective Rabi frequencies on the two target ions.
In this experiment, we only push the ions to about 7 μm from the RF null with a micromotion amplitude of about 420 nm. This is restricted by the stability of the crystal under large excess micromotion. Using a cryogenic ion trap, much larger 2D ion crystals can be stably trapped34, and we expect the ultimate limit for 2D individual addressing to be when the micromotion amplitude A becomes comparable to the ion spacing d ≈ 5 μm. According to Fig. 4c, in such cases the required laser intensity may be increased by about eight times to compensate the micromotion effect. Nevertheless, this does not restrict the gate fidelity because all the other noise sources like the spontaneous emission are rescaled as well.
Discussion
To sum up, we demonstrate the individual addressing of a 2D ion crystal by crossed AODs and achieve all-to-all connected two-qubit gates. For diagonal ion pairs, we develop an alternating gate sequence such that at most one ion needs to be addressed at any time. We further show that the gate fidelities on a 2D crystal is not limited by the micromotion which can be compensated by calibrating the intensity of the addressing beams. Our current two-qubit gate fidelities are restricted by the short laser and motional dephasing time, and can be improved by shortening and stabilizing the optical path and by locking the trap frequency in future upgrades. Also a more complete noise model with an experimentally measured noise spectrum may be used for better consistency between the theoretical prediction and the experimental gate fidelity, and for further optimization of the gate performance55.
Methods
Blade trap for 2D ion crystals with large optical access
Our blade trap for 2D ion crystals is sketched in Supplementary Fig. 2. The DC and the RF blades are at an angle of 40°, with their inner edges separated along the diagonal direction by 500 μm. With this configuration, when we apply zero voltage on the DC electrodes (thus no axial trapping), the two radial principal axes of the trap will be 45° from the symmetric axes of these blades, or about 5° from the x and y axes in the plot. We further apply a DC bias on the RF electrodes to split the two radial trap frequencies such that ωy ≫ ωx. Finally, we introduce a weaker axial trapping ωz by the voltage pattern on the five segments of each DC blade, which does not significantly change the radial principal axes. Therefore the obtained 2D crystal will locate close to the xz plane. This design gives us larger optical access to the ion crystal than the typical monolithic 3D ion traps. Apart from the counter-propagating Raman laser beams and the imaging system perpendicular to the ion plane, our system also allows a detection laser along the micromotion-free z direction and a Doppler cooling laser at 20° from the xz plane with equal angles to the x and z axes.
Correction of detection error
We use an EMCCD camera to collect the fluorescence from individual ions under 370 nm detection laser for a 1 ms duration. Due to the low NA of 0.34 of our homemade objective, the quantum efficiency of the EMCCD, and the loss on many optic elements, we have a relatively low photon collection efficiency, which restricts the single-shot detection fidelity. From the measured photon count distributions for the bright and the dark states, we estimate a detection infidelity of about 7% for each ion. Moreover, aberrations in the imaging system increase the size of each ion’s image and cause their overlap. This leads to crosstalk between different ions. In other words, an ion is more likely to be detected as bright when its adjacent ions are in the bright state. To calibrate this error, we prepare all the ions in by optical pumping and a microwave π/2 pulse. Ideally, there should be no correlation in the measured states for different ions, while experimentally we estimate an average detection crosstalk of about 1% from the measured correlations.
Although such errors limit the performance of single-shot measurements, we can still recover the probability distribution in the computational basis when only the expectation values are needed. For this purpose, first we prepare all the 16 computational basis states for the four-ion crystal by optical pumping into followed by a global microwave π pulse and/or several individually addressed single-qubit π pulses. To suppress the slow drift in the laser intensity and to enhance the single-qubit gate fidelity, we use the Tycko’s composite pulse sequence which consists of three sequential π pulses56. For each computational basis state, we repeat the preparation-detection sequence for 10000 times to estimate its distribution under the detection errors. This gives us a 16 × 16 matrix M whose columns are the distributions for each computational basis state.
Now for any quantum state to be measured, we obtain a vector of frequencies over the 16 possible states from the total T = ∑ifi repetitions. Our task is to find the most likely probability distribution such that the distribution Mp can generate the observed frequencies f following a multinomial distribution. This maximum likelihood estimation problem can be solved by numerically optimizing p under the constraint that all the probabilities are nonnegative. We further estimate the error bar of the recovered observable by Monte Carlo sampling from the theoretical probability distribution of f/T and computing the standard deviation of the simulated observables. For the data presented in the main text, we measure the population like Fig. 2a for T = 2000 repetitions, and we measure each data point for the Rabi oscillation like Fig. 1c and the parity oscillation like Fig. 2b for T = 200 repetitions.
Phase-modulated gate design
Our two-qubit entangling gates are realized by counter-propagating bichromatic 355 nm Raman laser beams with symmetric blue- and red-detuned frequency components50. We have a Hamiltonian in the form of a spin-dependent force as where j goes over all the target ions, k goes over all the phonon modes, ηk is the Lamb–Dicke parameter of Mode k with a frequency ωk and an annihilation operator ak, bjk is the mode vector of Ion j in Mode k, Ωj is the Raman Rabi frequency on Ion j, and μ is the symmetric detuning of the Raman laser. The motional phase and the spin phase are determined by the phases of the blue- and red-detuned components and on Ion j, and the spin operator on Ion j is defined as . By tuning and simultaneously, we can adjust the motional phase while keeping the spin phase a constant, which we define as the σx axis of the qubit. In the above Hamiltonian we have also performed rotating-wave approximation to drop the far-off-resonant terms.
The unitary evolution under the above Hamiltonian can be expressed as spin-dependent displacements of all the phonon modes together with two-qubit phases between the target ions . The displacement due to Ion j on Mode k is given by
| 1 |
which we want to suppress at the end of the gate. The two-qubit phase between ions i and j is given by
| 2 |
which appears from applying a new displacement dα to the accumulative one α(t) at different directions.
In this experiment, we use a phase-modulated gate sequence where we divide the whole gate into several equal segments and set the motional phase to be piecewise-constant on these segments. When we set the duration of each segment to be a multiple of 2π/∣μ − ωk∣ for some mode k, clearly the spin-dependent displacement vanishes independent of . For the LR and the UD ion pairs, we further cancel the spin-dependent displacement of the COM mode by a phase shift of Δϕ = π − (μ − ω1)ΔT between the two segments where ΔT is the time difference between the starting points of the two segments, namely the duration of a single segment.
As for the LU ion pair, after designing each segment to disentangle Mode 2 and Mode 4 as described in the main text, we still need to choose the phases of different segments to set the spin-dependent displacements of Mode 1 and Mode 3 to zero. This can be achieved using 22 = 4 segments49 in the pattern of [0, π − (μ − ω3) × ΔT, π − (μ − ω1) × 2ΔT, − (μ − ω3) × ΔT − (μ − ω1) × 2ΔT].Note that here we use the same phase sequence alternatingly on the two target ions, so we have ΔT = 2[4π/(ω2 − ω4) + Δt] covering two segments and separations. Such a phase sequence can accumulate a nonzero two-qubit phase between the two target ions according to Eq. (2), and we can scale the overall Raman Rabi rate of the laser to set this phase to ± π/4, which gives us the desired maximal entangling gate.
Finally, note that when applying the 355 nm Raman laser, there will be a differential AC Stark shift on the target ions on the order of kHz50. On the one hand, we can shift the blue- and red-detuned frequency components accordingly so that we still get a spin-dependent force in a suitable rotating frame. On the other hand, when switching the addressing beam between the two target ions, we are effectively switching between two frames and we need a shift in the spin phase to compensate it.
Gate error sources
To estimate the influence of various error sources, we calibrate their strength by separated single-ion or multi-ion experiments. The laser dephasing time is measured to be τs = 4 ms by fitting the exponential decay of the Ramsey fringes under the counter-propagating Raman π/2 pulses, and is mainly caused by the vibration of optical components in the relatively long optical path consisting of multiple layers. To separate its effect from the measurement of the motional dephasing time, we use the following sequence: First we initialize the ion in of the spin and the motional states by sideband cooling and optical pumping; Then we perform a carrier Raman π/2 pulse followed by a red-sideband Raman π pulse to prepare the superposition of the motional state ; After waiting for time t to accumulate some unknown phase between the motional states and due to the fluctuation of the trap frequency, we apply another red-sideband π pulse and another carrier π/2 pulse to turn this phase information into the population of the spin. Note that in this way the optical phase is canceled between the adjacent carrier and red-sideband pulses, and we fit a motional dephasing time of τm = 3 ms.
We estimate the average phonon number of the four normal modes in the y direction by comparing the excitation probability of the red and the blue motional sidebands54 under a weak individually addressed Raman laser. Then by fitting the increase of the average phonon number vs. the waiting time, we obtain the heating rate of the COM mode to be 120 s−1, and those of the other modes to be below 10 s−1.
The above error sources are modeled as Lindblad operators in our numerical analysis and are solved by QuTip57. As for the fluctuation of the laser intensity, we treat it as a low-frequency shot-to-shot variation. To estimate its strength, we set the Raman laser to a large detuning Δ such that its effect is mainly an AC Stark shift on the qubit. Then we perform the Ramsey spectroscopy using microwave π/2 pulses with this far-detuned Raman laser turned on during the waiting time. The intensity fluctuation thus translates into the phase noise and can be fitted from the Gaussian envelope of the Ramsey fringes. By comparing this decay rate with the oscillation frequency of the Ramsey fringes which is proportional to Ω2/Δ, we estimate a standard deviation of σ = 1% in the relative Raman Rabi frequency. Its effect on the gate fidelity will further be squared as (π2/4)σ2.
Supplementary information
Acknowledgements
This work was supported by Innovation Program for Quantum Science and Technology (2021ZD0301601), Tsinghua University Initiative Scientific Research Program, and the Ministry of Education of China. L.M.D. acknowledges in addition support from the New Cornerstone Science Foundation through the New Cornerstone Investigator Program. Y.K.W. acknowledges in addition support from Tsinghua University Dushi program. C.Z. acknowledges in addition support from the Shui-Mu Scholar postdoctoral fellowship from Tsinghua University. P.Y.H. acknowledges the start-up fund from Tsinghua University.
Author contributions
L.M.D. proposed and supervised the project. Y.H.H., Y.J.Y., Y.Y.C., L.Z., Y.W., Y.L.X., C.Z., Q.X.M., H.X.Y., J.Y.M., S.A.G., J.Y., B.X.Q., Z.C.Z., and P.Y.H. carried out the experiment. Y.K.W. did the theoretical gate design. Y.K.W., Y.H.H., Y.J.Y., and L.M.D. wrote the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The data supporting this work are available at Figshare 10.6084/m9.figshare.27143505 (ref. 58).
Competing interests
Y.W., C.Z., Q.X.M., H.X.Y., and J.Y.M. are affiliated with HYQ Co. Y.K.W., Y.W., Q.X.M., H.X.Y., J.Y.M., B.X.Q., Z.C.Z., and L.M.D. hold shares with HYQ Co. The other authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Y.-H. Hou, Y.-J. Yi, Y.-K. Wu.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-53405-z.
References
- 1.Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information (Cambridge University Press, 2000).
- 2.Acharya, R. et al. Suppressing quantum errors by scaling a surface code logical qubit. Nature614, 676–681 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bao, F. et al. Fluxonium: an alternative qubit platform for high-fidelity operations. Phys. Rev. Lett.129, 010502 (2022). [DOI] [PubMed] [Google Scholar]
- 4.Ballance, C. J., Harty, T. P., Linke, N. M., Sepiol, M. A. & Lucas, D. M. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett.117, 060504 (2016). [DOI] [PubMed] [Google Scholar]
-
5.Gaebler, J. P. et al. High-fidelity universal gate set for
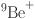 ion qubits. Phys. Rev. Lett.117, 060505 (2016).
[DOI] [PubMed] [Google Scholar]
ion qubits. Phys. Rev. Lett.117, 060505 (2016).
[DOI] [PubMed] [Google Scholar] - 6.Bluvstein, D. et al. Logical quantum processor based on reconfigurable atom arrays. Nature626, 58–65 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rong, X. et al. Experimental fault-tolerant universal quantum gates with solid-state spins under ambient conditions. Nat. Commun.6, 8748 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Noiri, A. et al. Fast universal quantum gate above the fault-tolerance threshold in silicon. Nature601, 338–342 (2022). [DOI] [PubMed] [Google Scholar]
- 9.Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett.127, 180501 (2021). [DOI] [PubMed] [Google Scholar]
- 10.Moses, S. A. et al. A race-track trapped-ion quantum processor. Phys. Rev. X13, 041052 (2023). [Google Scholar]
- 11.Chen, J.-S. et al. Benchmarking a trapped-ion quantum computer with 29 algorithmic qubits. arXiv:2308.05071 (2023).
- 12.Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A86, 032324 (2012). [Google Scholar]
- 13.Bruzewicz, C. D., Chiaverini, J., McConnell, R. & Sage, J. M. Trapped-ion quantum computing: progress and challenges. Appl. Phys. Rev.6, 021314 (2019). [Google Scholar]
- 14.Harty, T. P. et al. High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit. Phys. Rev. Lett.113, 220501 (2014). [DOI] [PubMed] [Google Scholar]
- 15.Clark, C. R. et al. High-fidelity bell-state preparation with 40ca+ optical qubits. Phys. Rev. Lett.127, 130505 (2021). [DOI] [PubMed] [Google Scholar]
-
16.An, F. A. et al. High fidelity state preparation and measurement of ion hyperfine qubits with
 . Phys. Rev. Lett.129, 130501 (2022).
[DOI] [PubMed] [Google Scholar]
. Phys. Rev. Lett.129, 130501 (2022).
[DOI] [PubMed] [Google Scholar] - 17.Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl. Inst. Stand. Technol.103, 259 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hughes, R. J., James, D. F. V., Knill, E. H., Laflamme, R. & Petschek, A. G. Decoherence bounds on quantum computation with trapped ions. Phys. Rev. Lett.77, 3240–3243 (1996). [DOI] [PubMed] [Google Scholar]
- 19.Clark, R. Proceedings of the 1st International Conference on Experimental Implementation of Quantum Computation: Sydney, Australia, 16–19 January 2001 (Rinton Press, 2001).
- 20.Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature417, 709–711 (2002). [DOI] [PubMed] [Google Scholar]
- 21.Duan, L.-M., Blinov, B. B., Moehring, D. L. & Monroe, C. Scalable trapped ion quantum computation with a probabilistic ion-photon mapping. Quantum Info Comput.4, 165–173 (2004). [Google Scholar]
- 22.Duan, L.-M. & Monroe, C. Colloquium: quantum networks with trapped ions. Rev. Mod. Phys.82, 1209–1224 (2010). [Google Scholar]
- 23.Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A89, 022317 (2014). [Google Scholar]
- 24.Stephenson, L. J. et al. High-rate, high-fidelity entanglement of qubits across an elementary quantum network. Phys. Rev. Lett.124, 110501 (2020). [DOI] [PubMed] [Google Scholar]
- 25.Britton, J. W. et al. Engineered two-dimensional ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature484, 489–492 (2012). [DOI] [PubMed] [Google Scholar]
- 26.Bohnet, J. G. et al. Quantum spin dynamics and entanglement generation with hundreds of trapped ions. Science352, 1297–1301 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Polloreno, A. M., Rey, A. M. & Bollinger, J. J. Individual qubit addressing of rotating ion crystals in a penning trap. Phys. Rev. Res.4, 033076 (2022). [Google Scholar]
- 28.Szymanski, B. et al. Large two dimensional Coulomb crystals in a radio frequency surface ion trap. Appl. Phys. Lett.100, 171110 (2012). [Google Scholar]
- 29.Wang, Y. et al. Coherently manipulated 2d ion crystal in a monolithic Paul trap. Adv. Quantum Technol.3, 2000068 (2020). [Google Scholar]
- 30.Xie, Y. et al. An open-endcap blade trap for radial-2d ion crystals. Quantum Sci. Technol.6, 044009 (2021). [Google Scholar]
- 31.Kato, A. et al. Two-tone Doppler cooling of radial two-dimensional crystals in a radio-frequency ion trap. Phys. Rev. A105, 023101 (2022). [Google Scholar]
- 32.Kiesenhofer, D. et al. Controlling two-dimensional Coulomb crystals of more than 100 ions in a monolithic radio-frequency trap. PRX Quantum4, 020317 (2023). [Google Scholar]
- 33.Qiao, M. et al. Tunable quantum simulation of spin models with a two-dimensional ion crystal. Nat. Phys.20, 623–630 (2024). [Google Scholar]
- 34.Guo, S.-A. et al. A site-resolved two-dimensional quantum simulator with hundreds of trapped ions. Nature630, 613–618 (2024). [DOI] [PubMed] [Google Scholar]
- 35.Shen, C. & Duan, L.-M. High-fidelity quantum gates for trapped ions under micromotion. Phys. Rev. A90, 022332 (2014). [Google Scholar]
- 36.Wang, S.-T., Shen, C. & Duan, L.-M. Quantum computation under micromotion in a planar ion crystal. Sci. Rep.5, 8555 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bermudez, A., Schindler, P., Monz, T., Blatt, R. & Müller, M. Micromotion-enabled improvement of quantum logic gates with trapped ions. N. J. Phys.19, 113038 (2017). [Google Scholar]
- 38.Ratcliffe, A. K., Oberg, L. M. & Hope, J. J. Micromotion-enhanced fast entangling gates for trapped-ion quantum computing. Phys. Rev. A101, 052332 (2020). [Google Scholar]
- 39.Wu, Y.-K., Liu, Z.-D., Zhao, W.-D. & Duan, L.-M. High-fidelity entangling gates in a three-dimensional ion crystal under micromotion. Phys. Rev. A103, 022419 (2021). [Google Scholar]
- 40.Duan, L.-M. & Yang, H.-X. Addressing control system and addressing control method. CN112749808B https://patents.google.com/patent/CN112749808B/en (2021).
- 41.Pu, Y. et al. Experimental realization of a multiplexed quantum memory with 225 individually accessible memory cells. Nat. Commun.8, 15359 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang, Y. et al. High-fidelity two-qubit gates using a microelectromechanical-system-based beam steering system for individual qubit addressing. Phys. Rev. Lett.125, 150505 (2020). [DOI] [PubMed] [Google Scholar]
- 43.Barredo, D., Lienhard, V., de Léséleuc, S., Lahaye, T. & Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature561, 79–82 (2018). [DOI] [PubMed] [Google Scholar]
- 44.Ebadi, S. et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature595, 227–232 (2021). [DOI] [PubMed] [Google Scholar]
- 45.Roman, C., Ransford, A., Ip, M. & Campbell, W. C. Coherent control for qubit state readout. N. J. Phys.22, 073038 (2020). [Google Scholar]
- 46.Edmunds, C. L. et al. Scalable hyperfine qubit state detection via electron shelving in the 2D5/2 and 2F7/2 manifolds in 171yb+. Phys. Rev. A104, 012606 (2021). [Google Scholar]
- 47.Kim, S., Mcleod, R. R., Saffman, M. & Wagner, K. H. Doppler-free, multiwavelength acousto-optic deflector for two-photon addressing arrays of rb atoms in a quantum information processor. Appl. Opt.47, 1816–1831 (2008). [DOI] [PubMed] [Google Scholar]
- 48.Pogorelov, I. et al. Compact ion-trap quantum computing demonstrator. PRX Quantum2, 020343 (2021). [Google Scholar]
- 49.Green, T. J. & Biercuk, M. J. Phase-modulated decoupling and error suppression in qubit-oscillator systems. Phys. Rev. Lett.114, 120502 (2015). [DOI] [PubMed] [Google Scholar]
- 50.Debnath, S. A programmable five qubit quantum computer using trapped atomic ions. Ph.D. thesis, University of Maryland, College Park (2016).
- 51.Jia, Z. et al. Angle-robust two-qubit gates in a linear ion crystal. Phys. Rev. A107, 032617 (2023). [Google Scholar]
- 52.Zhu, S. L., Monroe, C. & Duan, L.-M. Arbitrary-speed quantum gates within large ion crystals through minimum control of laser beams. Europhys. Lett.73, 485–491 (2006). [Google Scholar]
- 53.Leung, P. H. & Brown, K. R. Entangling an arbitrary pair of qubits in a long ion crystal. Phys. Rev. A98, 032318 (2018). [Google Scholar]
- 54.Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys.75, 281–324 (2003). [Google Scholar]
- 55.Kang, M. et al. Designing filter functions of frequency-modulated pulses for high-fidelity two-qubit gates in ion chains. Phys. Rev. Appl.19, 014014 (2023). [Google Scholar]
- 56.Tycko, R. Broadband population inversion. Phys. Rev. Lett.51, 775–777 (1983). [Google Scholar]
- 57.Johansson, J., Nation, P. & Nori, F. Qutip 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun.184, 1234–1240 (2013). [Google Scholar]
- 58.Yi, Y. Data used in "Individually Addressed Entangling Gates in a Two-Dimensional Ion Crystal". figshare. Dataset. 10.6084/m9.figshare.27143505.v1 (2024).
- 59.Wu, Y.-K. & Duan, L.-M. Progress on ion trap quantum computation and simulation using two-dimensional ion crystals. Science Bulletin In Press. 10.1016/j.scib.2024.09.025 (2024). [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data supporting this work are available at Figshare 10.6084/m9.figshare.27143505 (ref. 58).