A multimodal fusion network based on a cross-attention mechanism for the classification of Parkinsonian tremor and essential tremor

Abstract

Parkinsonian tremor (PT) and Essential tremor (ET) exist as upper limb tremors in clinical practice. Notably, their types of trembling share similar presentations and overlapping frequencies. To enhance objectivity and efficiency in the diagnosis of these two diseases, there is a pressing need for more objective tremor classification procedures. This study proposes a novel multimodal fusion network based on a cross-attention mechanism (MFCA-Net) to automate the classification of upper limb tremors between PTs and ETs. To this end, 140 patients with PTs and ETs were recruited, and acceleration and surface electromyography (sEMG) signals were collected from the forearm during tremor episodes. To comprehensively capture the global and local features of input signals, a multiscale convolution in MFCA-Net was designed. Furthermore, the cross-attention mechanism was applied to fuse the features of the two input signals. The results demonstrate that the final classification accuracy exceeded 97.18% when MFCA-Net was used. Compared with the single acceleration signal and single sEMG signal inputs, the recognition accuracies increased by 18.91% and 10.04%, respectively. Therefore, the proposed MFCA-Net in this study serves as an objective and potential tool for assisting clinicians in the diagnosis of PT and ET patients.

Introduction

Patients diagnosed with Parkinson’s disease (PD) and Essential tremor (ET) commonly experience involuntary convulsive movements, primarily affecting their limbs and head, and, in severe cases, the entire body. PD, a degenerative neurological disorder predominantly observed in elderly individuals, specifically involves the cerebellar–thalamic–cortical (CbTC) circuit in tremor genesis, with the basal ganglia also playing a modulating role¹. Rest tremor is the primary type of tremor observed in PD patients and occurs at frequencies between 4 and 6 Hz¹. Additionally, 48% of PD patients may exhibit action tremors, including postural tremors and intentional tremors². On the other hand, ET, a complex genetically linked condition, often peaks during two distinct age ranges: youth and beyond age 65. In approximately 30% of ET patients, tremors manifest as resting tremors at the distal ends of both upper limbs rather than typical postural tremors in the frequency range of 4–8 Hz^2,3. Despite the differences between PD and ET in their pathogenesis, Parkinsonian tremor (PT) and ET share similar presentations and overlapping frequencies for their respective types of trembling. Therefore, it is challenging to differentiate between these two diseases based solely on observable symptoms, such as trembling manifestations. Currently, computed tomography (CT)^4–6 serves as an essential diagnostic tool for identifying PD clinically by using positron emission computed tomography (PET) or single photon emission computed tomography (SPECT). These methods enable the radiolabeling of dopamine transporters. However, these methods, involving radioactive tracers, are typically costly, time-consuming, and invasive.

With the advent of wearable sensors, noninvasive methods based on motion sensing technology can gather information on users’ movements and postures through acceleration, angular velocity, and infrared optical signals. For PTs and ETs, wearable sensors capture motion signals for characterizing involuntary convulsive movements and assist in diagnosing these two diseases. Previous studies have demonstrated that motion signals are processed mostly by predetermined thresholds. For example, to identify PT and ET, Barrantes et al.⁷ extracted a new parameter called relative energy (RE) from acceleration signals with a recognition accuracy of 84.38% when the RE threshold was set to 0.21. Additionally, Thanawattano et al.⁸ employed the fluctuation ratio of angular velocity signals to distinguish three PT patients and two ET patients with zero error probability. Based on these studies, there is no doubt that the threshold approach can distinguish between patients with PTs and those with ETs. However, the relatively small number of subjects limits the ability to capture and quantify more detailed motion characteristics, especially for the tremor frequencies of PTs and ETs, which often overlap within the numerical range. Therefore, this research gap still needs to be filled.

To address the arbitrariness of threshold-based classification and enhance the comprehensive learning of tremor features, machine learning (ML) techniques have been introduced into tremor classification tasks to construct automated diagnostic systems. Recognition of PTs and ETs is usually conducted by training the extracted motion features with traditional ML models. For example, Loaiza Duque et al. employed two methods, namely, acceleration signals combined with quadratic discriminant analysis (QDA)⁹ and angular velocity signals combined with Ensemble Subspace K-Nearest Neighbors (ESKNN)¹⁰, to distinguish healthy people from tremor patients. To further subdivide patients with PT and ET, Loaiza Duque et al.¹⁰ trained a linear support vector machine (LSVM) model using two motion features extracted from angular velocity signals, i.e., the harmonic index ratio (HIR) and median power frequency (MPF), and the average recognition accuracy reached 77.8%. Statistical characteristics extracted from acceleration signals were employed to train ML classifiers, including decision trees (DTs), discriminant analysis (DA), support vector machines (SVMs), K-nearest neighbors (KNNs) and ensemble learning algorithms, which achieved recognition accuracies of over 90% in classifying PTs, ETs and subjects without tremors^11,12. Surface electromyography (sEMG) signals, another invasive motion sensing method, can reflect the muscle contraction intensity triggered by the action potential of the motor unit^13,14. For patients with PTs and ETs, their sEMG signals are measured by sEMG sensors attached to their forearms. These signals provide a wealth of information about the coactivation and coordination of extensor and flexor muscles, which are associated with different tremor characteristics. Povalej Bržan et al.¹⁵ and Sushkova et al.¹⁶ analyzed muscle activity with sEMG signals and employed ML models to distinguish PT from ET, achieving recognition accuracies of over 90%. To comprehensively capture the features of tremor behavior, multisensory fusion technology has also been employed for classifying patients with different types of tremors. Multisensory-based tremor classification focuses primarily on calculating and fusing predefined coefficients and parameters of multimodal signals, such as acceleration and angular velocity¹⁷, or acceleration and sEMG^18,19, to analyze the synergetic neuromuscular control or upper limb muscle coactivation of tremors in patients with PT and ET. However, predetermined characteristics or coefficients may not adequately represent the nonstationary and nonlinear sEMG signals detected in intricate tremor patterns.

Compared with traditional manual feature extraction, convolutional neural networks (CNNs) automate the process by performing convolution on input data to obtain high-level features. CNNs automatically update convolutional kernel parameters via a gradient descent algorithm to extract semantic information from input data²⁰. This process minimizes subjectivity in the model training process and holds the potential to design an end-to-end tremor classification system. With three-dimensional hand data recorded from 40 patients with tremors by the Leap Motion Controller (LMC), Oktay et al.²¹ developed a model that combines CNNs and long short-term memory (LSTM) to classify PTs and ETs and reached a classification accuracy of 90%. By increasing the number of hidden layers of CNNs, Hathaliya et al.²² applied seven hidden layers with various convolution kernel sizes to learn the feature representations of acceleration signals and finally achieved an accuracy of 92.4% in PT recognition on the basis of tremor intensity. Shahtalebi et al.²³ proposed a data-driven NeurDNet model, which trains hand acceleration signals from 81 subjects with PT and ET and finally achieves a recognition accuracy of 95.55%. However, current research on tremor classification via deep learning focuses mostly on the use of a single signal as the model’s input. In contrast, fusing two types of signals as the input for CNNs was first applied to classify PT and ET by Xing et al.²⁴. In Xing’s study²⁴, the acceleration and sEMG signals were fused to two-dimensional arrays in the frequency domain, ultimately achieving 78% classification accuracy. This study represents initial attempts to combine multisensory signals as the input of CNNs. To the best of our knowledge, no further research has focused on the impact of multisensory signals on PT and ET classification via deep learning.

Considering the limitations of clinical diagnosis and the ability of sensor technologies to capture motion and neuromuscular characteristics, this work proposed a novel approach to objectively distinguish tremor patients via multisensory signals fusion. Specifically, an automatic multiscale CNN-based framework that combines acceleration and sEMG signals and learns not only intuitive motion parameters during tremors but also neuromuscular information was proposed. To further improve the recognition performance of tremor patients, a multiscale CNN based on a cross-attention mechanism was designed to extract and fuse the characteristics of acceleration and sEMG signals. In summary, this approach only requires patients to measure their acceleration and sEMG signals during tremors to automatically identify PT and ET patients. This approach can assist clinicians in primary screening and, to some extent, shorten the diagnostic time.

Materials

Participants

This study included 140 patients with PTs (87) and ETs (53), and the mean age was 66.23 ± 30.85 years. The exclusion criteria were as follows: (1) Other neurological diseases (such as multiple sclerosis, Alzheimer’s disease, etc.); (2) Drug action (such as antipsychotic drugs, sedatives, etc.); (3) Serious cognitive impairment (Mini-Mental State Examination score less than ten points); and (4) Other diseases (such as heart disease and lung disease). The type of tremor in the participants was diagnosed by Ruijin Hospital neurology experts (Shanghai, China). Following the clinical diagnosis, the severity of the disease and tremors was assessed via the UPDRS for PT patients and the FTM for ET patients. Specifically, according to the third part of the UPDRS (UPDRS-III), the total score for PT patients ranges from 5 to 68 points (mean ± standard deviation: 26.7 ± 10.3), whereas according to the FTM, the total score for ET patients ranges from 10 to 78 points (mean ± standard deviation: 41.2 ± 13.6). To investigate the clinical similarities among patients, we selected tremor-related sections of the UPDRS-III for comparison with the FTM, yielding scores ranging from 5 to 36 points. For these two scales, each subitem is scored from 0 to 4. The severity of tremors can be classified into three levels on the basis of these scores. Specifically, if all subitem scores are between 0 and 2, mild tremors are indicated. If any score is 3 and none are 4, it indicates moderate tremors. A score of 4 indicates severe tremors. The number of patients with different tremor levels according to these classifications is shown in Table 1. All the participants’ caregivers signed informed consent prior to the experiment, and all the experiments were performed in accordance with relevant guidelines and regulations. The experimental protocol was evaluated and approved by the Ruijin Hospital Ethics Committee of Shanghai Jiao Tong University School of Medicine (No. 2023 − 359).

Table 1.

Number of patients with different tremor levels.

Tremor level	PT	ET
Mild tremor	36	21
Moderate tremor	43	27
Severe tremor	8	5

Postures and muscles

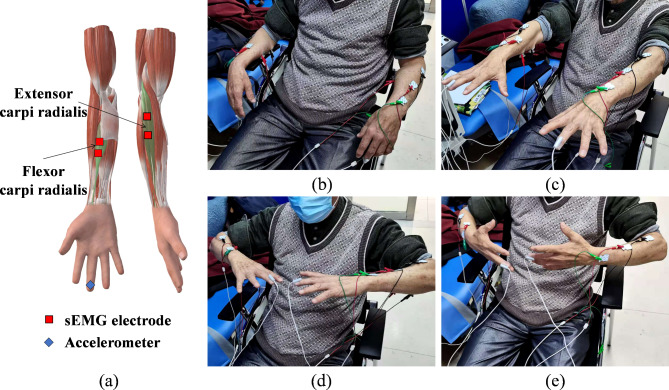
To better capture resting tremors and postural tremors, this study designed four postures: rest, stretch, wing, and vertical wing. During the data collection experiment, all the subjects were asked to sit on the chair and keep their backs against the chair. The knees were then bent at 90 degrees with their feet flat on the floor. The rest posture is defined as having the upper limbs supported on the armrests of the chair, with the arms relaxed and stationary. The stretch posture requires the arms of the upper limbs to be straight and held parallel to the floor, with the palms facing down. The wing posture involves bending the arms at the elbows and holding them flat and parallel to the floor, with the palms facing down. The vertical wing posture entails bending the arms at the elbows and holding them flat and parallel to the ground, but with the palms facing the sides of the body. Considering that the arm will bear most of the weight in daily life, the participants were asked to add a kilogram of weight to their wrists while maintaining the stretch, wing, and vertical wing postures. Each participant was required to maintain the above seven states (rest, stretch, wing, vertical wing, 1-kg weight-bearing stretch, 1-kg weight-bearing wing, and 1-kg weight-bearing vertical wing), and every posture was maintained for 30 s. Considering that the action of tremors is related to muscles, the extensor carpi radialis and flexor carpi radialis of the forearms of both upper limbs were selected for this study. The specific postures and related muscles are shown in Fig. 1.

Fig. 1.

Tremor signal acquisition. a Placement of the accelerometers and sEMG electrodes. The four postures shown in the image on the right are b rest, c stretch, d wing, and e vertical wing.

Tremor data acquisition

A signal acquisition system, Dantec Keypoint, was used to record participants’ tremor signals, which included acceleration signals and sEMG signals. The sEMG sensor electrodes were placed on the extensor carpi radialis and flexor carpi radialis. Two accelerometers were fixed on the far ends of the middle fingers of both hands. The detailed placements are depicted in Fig. 1a. The sample frequency of acceleration and sEMG signals was 12,000 Hz. The participants were required to remain seated throughout the experiment, and hospital staff were not permitted to enter or exit the room to eliminate unrelated variables.

Methods

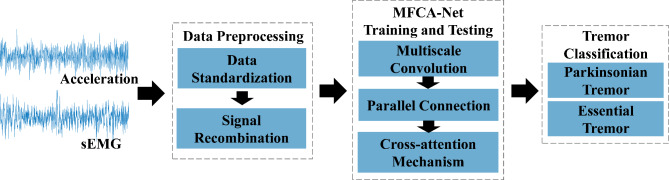
This section describes the approaches for PT and ET classification and is divided into three parts to introduce the construction of the PT and ET automatic classification model. First, data preprocessing was performed. Second, a multimodal fusion network based on a cross-attention mechanism (MFCA-Net) is constructed. Third, parameters related to model training and the evaluation metrics for model testing were developed. Figure 2 shows the detailed process of the PT and ET classification. The VSCode integrated programming environment for Python served as the signal preprocessing platform. TensorFlow 2.5.0 is a Python library upon which the proposed model is based. A computer equipped with an Intel(R) Xeon(R) Platinum 8255 C CPU @ 2.50 GHz and an RTX 2080 Ti GPU with 11 GB RAM was used for model training.

Fig. 2.

Framework of PT and ET classification. The acceleration and sEMG data were preprocessed and then input into MFCA-Net for training and testing.

Data preprocessing

Signal preprocessing includes two steps. First, the per-channel signal acquired from the participant in one posture was represented as a matrix, where the acceleration signal was denoted as 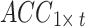and the sEMG signal as 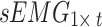, with t representing the acquired signal length. The signal of each channel was standardized via the Z score. This process transforms the data into a distribution with a mean of 0 and a standard deviation of 1. Equations (1) and (2) outline the specific process.

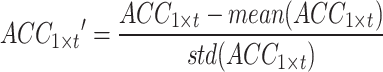1

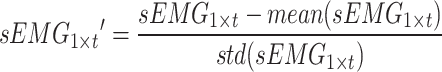2

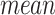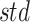where and represent the average and standard deviation of the signals, respectively. 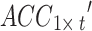and 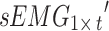are single-channel data of standardized acceleration and sEMG signals, respectively.

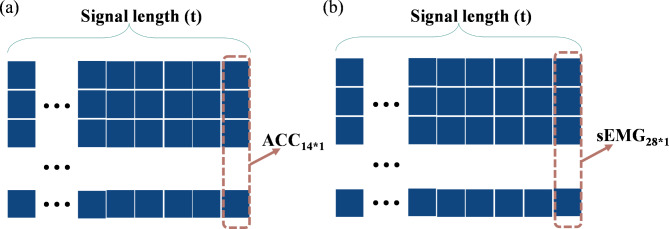
Second, to simultaneously obtain the signal features of different postures, the standardized acceleration and sEMG signals for the seven postures were separately recombined, as shown in Fig. 3. Specifically, the number of channels for the unilateral upper limb acceleration signal acquired from each participant in one posture is defined as m (m = 1), and the number of channels for the sEMG signal is defined as n (n = 2). Therefore, after standardizing the acceleration and sEMG signals of each channel with the Z score, the acceleration signal acquired from the bilateral upper limbs in one posture can be represented by the matrix 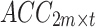, whereas the sEMG signal can be represented by the matrix 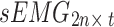, where t denotes the signal length. To simultaneously acquire tremor signals from the bilateral upper limbs in seven postures (rest, stretch, wing, vertical wing, 1-kg weight-bearing stretch, 1-kg weight-bearing wing, and 1-kg weight-bearing vertical wing), this study recombined the signals into the following instructions: (1) The acceleration signals collected from the bilateral upper arms in the seven postures were recombined into a matrix 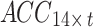; and (2) the sEMG signals collected from the bilateral upper arms in the seven postures were recombined into a matrix . 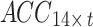Both and 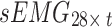were used as the acceleration and sEMG inputs to the model, respectively.

Fig. 3.

Signal recombination and the input format of the model. a Input form of the acceleration signal. b Input form of the sEMG signal.

MFCA-Net

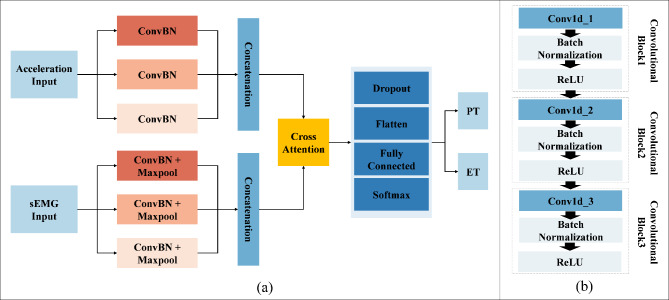
In this study, MFCA-Net was proposed to assist in the recognition of PTs and ETs. The MFCA-Net framework is illustrated in Fig. 4. The goals of MFCA-Net are twofold: (1) acquire a feature map with multiscale receptive fields and (2) fuse the signal features from different modes, i.e., acceleration and sEMG modes. MFCA-Net consists of a feature extraction layer, feature fusion layer, dropout layer, fully connected layer, and softmax activation function. In the initial phase of MFCA-Net, ConvBN and pooling layers were employed to obtain feature maps with different receptive fields to enhance the feature information of the input data. The cross-attention mechanism was subsequently employed to selectively merge the previously extracted characteristics. Finally, the dropout rate was set to 0.5 to prevent overfitting during network training, and then the feature map was expanded through the flatten layer so that the fully connected layer could better capture its complex structure and increase the expressive ability of the model. The following sections provide the details of the aforementioned modules.

Fig. 4.

MFCA-Net framework. a Frame diagram of MFCA-Net. b ConvBN block, which includes three convolutional blocks, with each block consisting of a convolution layer, a batch normalization layer and a ReLU activation function.

Multiscale convolution

To enhance the ability of deep CNNs to extract features at different scales, recent research has predominantly employed multiscale convolution approaches to fuse comprehensive feature data. Jia et al.²⁵ and Supratak et al.²⁶ constructed multistream CNNs to extract temporal characteristics from electroencephalography data at various scales. Compared with stacking different convolutional and pooling layers, multiscale convolution better captures both local and global information from nonstationary and nonlinear signals, such as sEMG. It also enables the network to adapt more efficiently to signals of varying sizes.

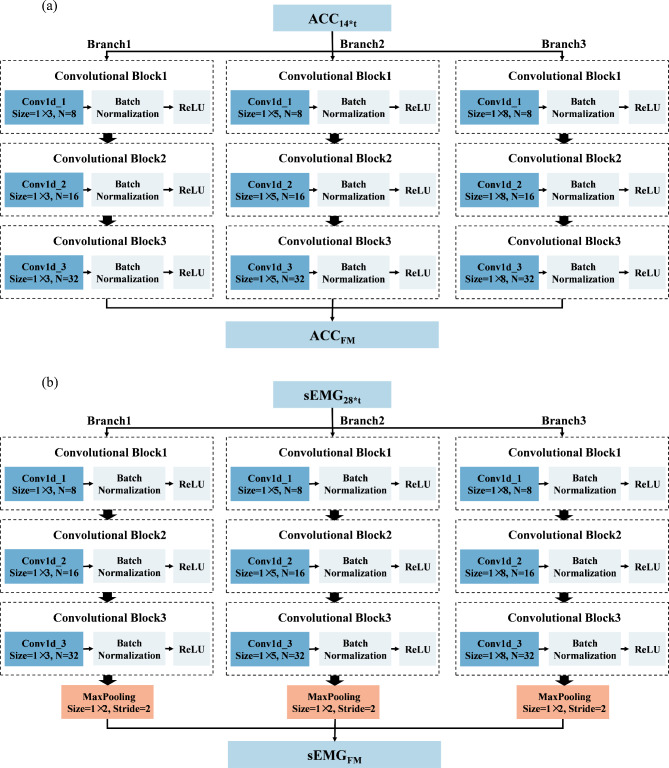
In this study, two networks were constructed using multiscale convolution to extract features from acceleration and sEMG signals. Each network consists of three branches, corresponding to convolutional filters of sizes 3, 5, and 8. For the acceleration feature extraction module, each branch consists of a series of one-dimensional convolution layers, batch normalization layers, and ReLU activation functions. Additionally, a Max-pooling layer was applied to each branch in the sEMG feature extraction module to reduce the feature dimensionality and select important features for subsequent fusion with the acceleration features. The detailed structure of the feature extraction module, including the network parameters, is illustrated in Fig. 5. Using the constructed multiscale feature extraction module, the input feature matrices 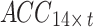and 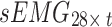were continuously processed and learned to produce high-level feature mappings 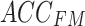and .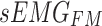

Fig. 5.

Multiscale feature extraction module. a Multiscale convolution module for acceleration. b Multiscale convolution module for sEMG. The branches of the two signal feature extraction modules present the same structure, whereas the filter sizes differ. ‘Size’ and ‘N’ in the convolution layers represent the size and number of convolution filters, respectively, and the stride of the convolution kernel was set to the default value of 1. ‘Size’ and ‘Stride’ in the pooling layers represent the pool size and pool stride.

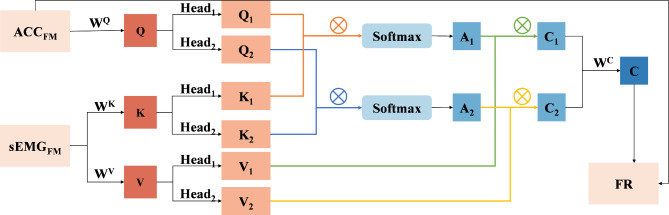
Cross-attention mechanism

The purpose of this study is to classify PTs and ETs by fusing acceleration and sEMG signals. Traditional multimodal fusion in CNNs includes concatenation or summation. Despite its simplicity, this fusion technology still lacks adaptability, especially when dealing with issues of data imbalance and multimodal heterogeneity²⁷. This limitation can be addressed by the cross-attention mechanism, which aligns the incompatible feature space of cross-mode signals and enhances the representative features of each signal acquisition. Consequently, the cross-attention mechanism enhances the interaction between acceleration and sEMG signals, enabling the feature vector to better capture data from two modes.

To enhance the model’s representation ability and robustness, the multihead attention mechanism is commonly employed. This mechanism calculates and merges multiple groups of attention weights in parallel, followed by linear transformation to obtain the final output. Therefore, in this study, a one-dimensional multihead cross-attention mechanism was applied to establish a connection between the feature maps 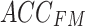and 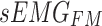, derived from the feature extraction module, and weights were assigned to them, producing the fused results, denoted as 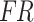. The details are illustrated in Fig. 6.

Fig. 6.

Cross-attention module in MFCA-Net. The orange and blue arrows represent the dot products of the two heads against the query and key, respectively, whereas the green and yellow arrows represent the dot products of the attention weights with the sequence of values.

The cross-attention module receives inputs from the feature mappings of acceleration and sEMG signals, designated as the target sequence (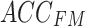) and source sequence (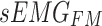), respectively. According to Eqs. (3–8), the query sequence, key sequence and value sequence are obtained through linear transformation, and these sequences are divided into two headers.

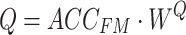3

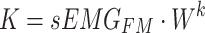4

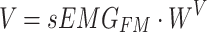5

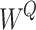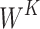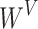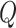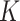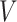where , and are learning weight parameters and where , and represent the query sequence, key sequence and value sequence, respectively.

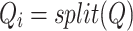6

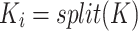7

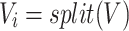8

where 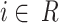represents the index of each head and the maximum of 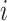was set to 2 in this study.

To capture the relationships between queries and keys, 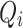and 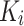are dot-producted and scaled, and their attention weights are obtained via the Softmax function. The specific details are provided according to Eq. (9).

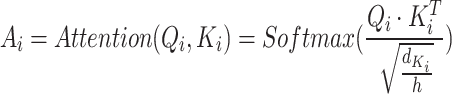9

where 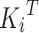denotes the transpose of 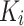, h is the number of heads and 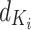represents the dimensionality of 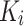. The 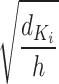is set up to scale the attention weights and keep the value of the dot product from increasing too much.

Then, the attention weights are applied to 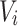to obtain the weighted value sequence, as described in Eq. (10).

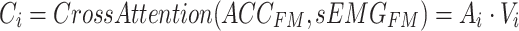10

where 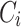represents the attention output of each head.

According to Eq. (11), the attention outputs 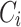of all heads are concatenated together along the last dimension, resulting in the multihead attention output 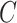. Then, 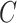is linearly transformed and mapped back to the original dimension. Finally, Eq. (12) is used to combine the obtained weighted value sequences with 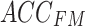, producing the output of the cross-attention mechanism.

11

where 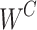represents the learning weight parameters.

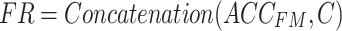12

where 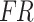denotes the fused results obtained by applying the cross-attention mechanism to feature mappings of acceleration and sEMG signals.

Fully connected neural network

A dropout rate of 0.5 was applied when passing the output 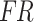of the cross-attention module through the dropout layer. During training, the dropout layer randomly zeros out certain input components with a predetermined probability, which helps prevent the model from overfitting and enhances model generalizability. The output of the dropout layer was straightened by the flatten layer and then organized into a one-dimensional array as the input for the fully connected layers. Following the fully connected layer, the Softmax activation function was used to achieve the final classification.

Model training

After data preprocessing, the dataset of 140 samples was split into a training set and a test set at a 7:3 ratio, with 20% of the training data allocated as a validation set. The cross-entropy loss function, which evaluates the difference between the ground-truth class distribution and the predicted probability distribution, was selected to guide model optimization. For optimization, the Adam optimizer was employed to optimize the gradient descent process, with a learning rate set to 0.001. Additionally, the model needs to be optimized iteratively during training to gradually improve and eventually stabilize its performance. This process can be monitored by observing changes in loss values. Specifically, when the loss values of both the training and validation sets gradually decrease until the change is less than 0.01 within five consecutive training rounds, the model is considered to have reached a converged state, indicating that the model has gained the ability to recognize PTs and ETs.

Model evaluation

To evaluate the model’s performance, the samples were classified as false-positives (FPs), false-negatives (FNs), true positives (TPs), and true negatives (TNs) based on the combination of the true labels and prediction labels, and these results were depicted in a confusion matrix. These classification metrics were then used to calculate specific evaluation metrics, such as accuracy, precision, recall, and the F1 score. Additionally, a receiver operating characteristic (ROC) curve was generated to provide a comprehensive view of the classification performance. In the ROC curve, the true positive rate (TPR) is represented on the vertical axis, whereas the false-positive rate (FPR) is represented on the horizontal axis. A larger area under the ROC curve (AUC) indicates better performance.

Experimental results

Training process

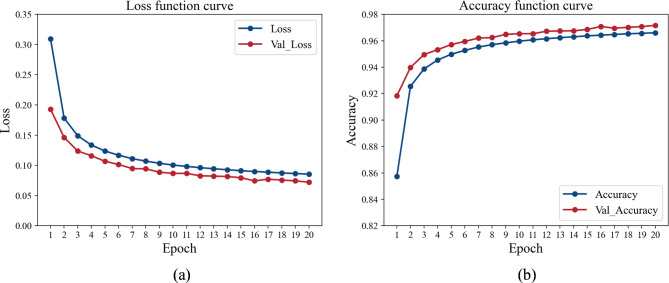
The proposed MFCA-Net was trained and validated by inputting the preprocessed sEMG and acceleration signals. Figure 7 illustrates the training fitting process of MFCA-Net proposed in this study. The results indicated that the accuracy and loss of both the training and validation sets gradually converged after 20 iterations of updates.

Fig. 7.

Model convergence during training. The blue lines denote the results of the training set, and the red lines indicate the results of the validation set. a Cross-entropy loss reduction curves during model training. b Accuracy changes during the model training process.

Results of MFCA-Net

After 20 rounds of training, MFCA-Net gradually fits the input data of both the training and validation sets, as shown in Fig. 7. To assess the generalization ability and performance of the model, the data from the test set were input into the trained MFCA-Net for inference and prediction. The detailed classification results and confusion matrix are presented in Table 2. The accuracy of MFCA-Net on the test set was 97.18%, and the AUC was 0.9696. Additionally, the precision and recall of the model also performed well for various classes. These results indicate its strong generalizability when faced with unprecedented data. This decent classification performance provides reliable support for distinguishing PT from ET, demonstrating significant potential for practical applications.

Table 2.

Confusion matrix and classification results.

True Label	Predicted Label		Precision	Recall	F1-score
	ET	PT
ET	96.04%	3.96%	96.49%	96.04%	96.27%
PT	2.13%	97.87%	97.59%	97.87%	97.73%
Accuracy = 97.18% & AUC = 0.9696

Ablation experiments

To verify the effectiveness and contribution of each module in MFCA-Net, two groups of experiments were designed. The first experiment evaluated the role of the cross-attention mechanism in MFCA-Net. The second experiment evaluated the influence of single-modal signals and multimodal signals on the performance of the PT and ET classification tasks.

Influence of the cross-attention module

This experiment replaces the cross-attention mechanism module in MFCA-Net with the feature concatenation method to investigate the effectiveness of the cross-attention mechanism in MFCA-Net. The new model using the concatenation method was defined as the control group (FCG). The original MFCA-Net model and the new model without the cross-attention mechanism were trained with the same training samples and parameter settings. After completing the model training, the test set was used to evaluate the two models and compare their performance. The comparative results are shown in Table 3. The overall accuracy of the FCG model was 91.33%, whereas the MFCA-Net model achieved a higher accuracy of 97.18%. For the other evaluation metrics in Table 3, the results of MFCA-Net also surpassed those of the FCG.

Table 3.

Classification results of MFCA-Net and FCG.

Model	Accuracy	Average Precision	Average Recall	Average F1-score	AUC
MFCA-Net	97.18%	97.04%	96.96%	97.00%	0.9696
FCG	91.33%	91.11%	90.36%	90.71%	0.9036

Influence of the multimodal inputs

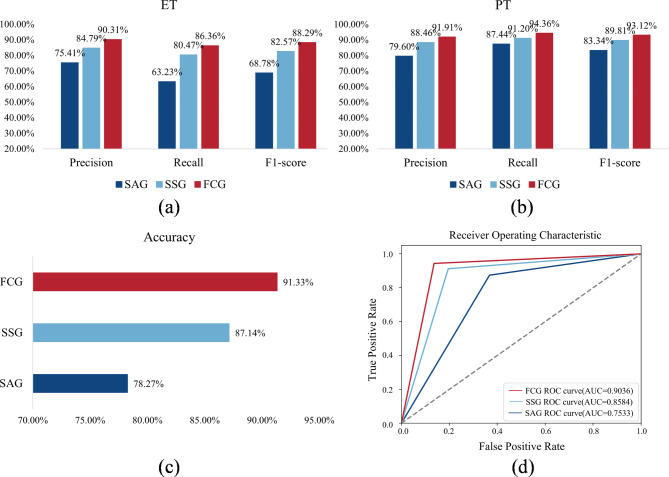
This experiment explored the performance of the single-modal signal and multimodal signal. To this end, the FCG with the fusion of acceleration and sEMG signals was defined as the experimental group, and the control groups were the single acceleration signal group (SAG) and the single sEMG signal group (SSG), respectively. When SAG is executed, the input of the sEMG signal in MFCA-Net is removed to ensure that the input contains only the acceleration signal. Similarly, MFCA-Net with an SSG was also input solely by the sEMG signal. The experimental group and the control groups were trained separately with the same training data and parameter settings. Figure 8 shows the classification results of the SAG, SSG and FCG. Specifically, the multimodal signal feature fusion method reached an accuracy of 91.33%, with an AUC of 0.9036. The recall value of ET was 86.36%, with 13.64% of ET incorrectly classified as PT. Additionally, the recall value of PT was 94.36%, with only 5.64% of PT incorrectly classified as ET.

Fig. 8.

Classification results of the SAG, SSG and FCG. a Comparison of precision, recall, and F1 score for ET. b Comparison of precision, recall, and F1 score for PT. c Comparison of overall accuracy. d Comparison of the ROC and AUC values.

When a single sEMG signal was used as input, the accuracy reached 87.14%, and the AUC reached 0.8584. For ET, the recall value was 80.47%, with 19.53% incorrectly classified as PT. For PT, the recall value was 91.20%, with only 8.80% incorrectly classified as ET. Using a single acceleration signal as input yielded an accuracy of 78.27% and an AUC of 0.7533. The recall value for ET was 63.23%, with 36.77% of ET incorrectly classified as PT. Conversely, the recall rate of PT was 87.44%, with only 12.56% of PT incorrectly classified as ET. The recall value for ET was lower than that for PT, possibly because there were fewer ET patients in this study than PT patients. This imbalance may have resulted in the model learning less tremor information for ET than for PT. In general, the classification accuracy when only the sEMG signal was used as the input was higher than that when only the acceleration signal was used. However, the classification accuracy improved when features from both acceleration and sEMG signals were combined, which indicates that the feature fusion method helps enhance the model’s feature learning ability and improves its classification performance.

Discussions

In this study, the automatic classification of PTs and ETs was implemented via MFCA-Net. To facilitate a clearer comparison with previous studies and highlight the practical application of our proposed model, Table 4 summarizes related studies on the classification of PT and ET in the field of ML. Most research has focused on distinguishing tremor signals via traditional ML techniques, such as LR and LSVM, and has yielded favorable classification results. Recently, the focus of PT and ET classification research has shifted from traditional ML to deep learning, particularly CNNs, which offer the advantage of automatically learning the characteristics of nonlinear data. However, most studies have been limited to using only one sensor to distinguish PTs and ETs, and the potential of deep learning methods in exploring the role of multisensory data in PT and ET classification has not been fully explored. To date, only one study has attempted to distinguish PT from ET by fusing multisensory signals (sEMG and acceleration signals) through deep learning²⁴. Specifically, Xing et al.²⁴ utilized fast Fourier transform (FFT) to transform the original acceleration and sEMG signals into the frequency domain, selecting and combining signals between 2 and 20 Hz as inputs for a two-layer CNN model. Ultimately, their recognition accuracy for PT and ET reached 78%.

Table 4.

Review of literature on tremor classification.

Author	Sensor	Sensor Placement	Movement	Scale	Subjects	Method	Results
Duque et al.9	ACC	Dorsum of the hand	Rest position; Arms stretched	FTM UPDRS (1 or 2)	17 PT, 16 ET	LR	Sensitivity = 66.7% Specificity = 84.8%
Duque et al.10	GYR	Dorsum of the hand	Rest position; Arms stretched	FTM UPDRS (1 or 2)	19 PT, 20 ET	LSVM	Accuracy = 77.8%
Ferreira et al.17	ACC & GYR	Dorsum of the hand	Rest position; Arms stretched	/	27 PT, 10 ET, 7 PD	KNN/NB	Accuracy = 93.33%
Oktay et al.21	LMC	Below the hand	Rest position; Arms stretched	HYS	23 PT, 17 ET	CNNs + LSTM	Accuracy = 90.0%
Shahtalebi et al.23	ACC	Dorsum of the hand	Rest positions; Postural positions; Weight-bearing tasks; Kinetic task	/	47 PT, 34 ET	CNNs + QDA	Accuracy = 95.55%
Xing et al.24	ACC & sEMG	Distal finger; Extensor and flexor	Rest; Stretch; Wing; Vertical wing	/	257 PT, 141 ET	CNNs	Accuracy = 78.0%
Ours	ACC & sEMG	Distal finger; Extensor and flexor	Rest; Stretch; Wing; Vertical wing;	FTM UPDRS (0–4)	87 PT, 53 ET	CNNs	Accuracy = 97.18%

ACC accelerometer, GYR gyroscope, LMC leap motion controller, sEMG sEMG sensors, NB naive Bayes, FTM (scale for ET) Fahn-Tolosa-Marin, UPDRS (scale for PT) unified Parkinson’s Disease Rating Scale, HYS (scale for PT) Hoehn and Yahr score.

In contrast, our work achieves fusion of acceleration and sEMG signals through the cross-attention mechanism, resulting in a final recognition rate of distinguishing PTs from ETs reaching 97.18%. According to Table 2, the results collectively indicate that our proposed CNN classification framework, which is based on multimodal signals, holds great potential and can serve as a valuable tool for distinguishing PTs and ETs via auxiliary diagnostic equipment.

While the use of single-sensor data for PT and ET classification has yielded some outcomes, it may still face challenges such as data limitations, incomplete information, and limited model generalizability. Therefore, it is crucial to consider employing multisensory data to obtain more comprehensive tremor information, thereby enhancing the performance and robustness of the classification model. As illustrated in Fig. 8, the accuracy of FCG is 91.33%, whereas the classification accuracies of SAG and SSG are 78.27% and 87.14%, respectively. The classification results obtained by simply combining acceleration and sEMG signals are much higher than those obtained by a single signal. These findings suggest the potential of exploring feature information from different sensor data sources to extract more discriminative feature representations for classification tasks.

In feature fusion tasks, concatenation is one of the most commonly used methods. This approach involves concatenating feature vectors from acceleration and sEMG signals based on the channel dimension, thereby creating a longer feature vector or matrix to facilitate data fusion. Conversely, the cross-attention mechanism automatically learns the correlation between features from different sources and assigns them weight distributions, thereby achieving more efficient feature fusion. As shown in Table 3, the classification accuracy achieved by combining acceleration and sEMG signals through concatenation is 91.33%, whereas the accuracy attained via the cross-attention mechanism reaches a noTable 97.18%. These fusion results from concatenation and the cross-attention mechanism align well with the earlier discussion, which demonstrates that the cross-attention mechanism captures the intricate relationship between acceleration and sEMG signals more effectively, thereby enhancing the accuracy and robustness of the classification model.

Conclusions

To the best of our knowledge, no prior deep learning model has achieved such high accuracy in tremor classification from acceleration and sEMG signals. Building on this foundation, this study introduces several innovations. First, multiscale CNNs apply convolution kernels of different sizes to the input data, allowing the model to extract and fuse feature representations with a rich spatial hierarchical structure. Additionally, to facilitate multimodal fusion, i.e., the fusion of acceleration and sEMG signals, a cross-attention module was incorporated to improve the fusion efficiency. The experimental results demonstrate that integrating multimodal signals significantly improves the performance of CNNs in PT and ET classification. Moreover, the cross-attention module enhances feature interaction, thereby further enhancing the model’s generalization performance and robustness. Overall, these findings affirm that MFCA-Net has superior recognition ability for PT and ET, whether compared with previous methods or assessed through ablation experiments. Consequently, MFCA-Net has demonstrated its potential as an objective and lightweight tool for clinicians to diagnose PT and ET patients.

Although the proposed MFCA-Net achieves better results in PT and ET classification tasks on the basis of multimodal signal fusion, it has several limitations. First, since the evaluation items of the two scales used in this study differ in the similarity analysis of participants’ tremors, it is difficult to make a completely fair comparison of the tremor similarity between PTs and ETs. To analyze the similarity of the two types of tremors more accurately, we will evaluate the severity of tremors by analyzing the parameters that characterize the tremors of the participants²⁸ or seeking a more specialized tremor scale in future work. Additionally, the participants in this study covered all tremor levels, and further classification of PT and ET with different tremor levels should be considered in future research. Second, this study is limited in its ability to differentiate between PT and ET tremors. However, other patients may also have similar tremor disorders (e.g., cerebellar tremor). In the future, more subjects with similar tremor presentations but different diseases will be recruited to expand our research, with the goal of developing a more comprehensive model for classifying patients with different types of tremors.

Author contributions

Lu Tang and Qianyuan Hu: methodological study, experimental design, model development, original manuscript writing; Xiangrui Wang and Long Liu: methodological study, manuscript editing; Hui Zheng and Wenjie Yu: model validation, result visualization; Ningdi Luo and Jun Liu: data collection; Chengli Song: experimental guidance. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 51735003).

Data availability

Our private Parkinsonian tremor and Essential tremor data generated and analyzed in this study are available on request from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.

Ethics statement

The study involving human participants was reviewed and approved by the Ruijin Hospital Ethics Committee of Shanghai Jiao Tong University School of Medicine (No. 2023 − 359). Patients/participants provided written informed consent to participate in this study. All the experiments were performed in accordance with the relevant guidelines and regulations.