Artificial intelligence in prostate cancer: The potential of machine learning models and neural networks to predict biochemical recurrence after robot-assisted radical prostatectomy

ABSTRACT

Introduction:

This study aimed to evaluate the usefulness of machine learning (ML) and neural network (NN) models versus traditional statistical methods for estimating biochemical recurrence (BCR) in men following robot-assisted radical prostatectomy (RARP).

Methods:

Patients who underwent RARP from November 2011 to July 2022 were taken in the study. Patients with BCR were assigned to Group 2, whereas those without BCR were placed in Group 1. Preoperative and postoperative parameters, together with demographic data, were recorded in the database. This study used one NN, the radial basis function NN (RBFNN), and two ML approaches, the K-nearest neighbor and XGboost ML models, to predict BCR.

Results:

Following the application of exclusion criteria, 516 patients were deemed eligible for the study. Of those, 234 (45.3%) developed BCR, and 282 (54.7%) did not. The results showed that the median follow-up period was 24 (15–42) months, and the median BCR diagnosis was 12.23 ± 15.58 months. The area under the curve (AUC) for the Cox proportional hazard analysis was 0.77. The receiver-operating characteristic curves (AUCs) for the XGBoost and K closest neighbor models were 0.82 and 0.69, respectively. The RBFNN’s AUC was 0.82.

Conclusions:

The classical statistical model was outperformed by XGBoost and RBFNN models in predicting BCR.

INTRODUCTION

Artificial intelligence (AI) includes machine learning (ML) and neural networks (NNs). The collected patient data may have intricate linkages and patterns that traditional statistical approaches are unable to uncover, particularly when working with large databases. AI can make it possible to design innovative and intuitive algorithms.[1]

Among men’s cancers, prostate cancer (PCa) is the second-most common cause of death.[2] Biochemical recurrence (BCR) is diagnosed in 27% of the patients and is associated with metastasis and mortality in patients after radical prostatectomy (RP).[3] Most of these recurrences occur during the initial 2 years after RP.[3,4] Evidence indicates that timely identification of patients at greater risk for BCR and prompt diagnosis and treatment of BCR result in the customization of patient care approaches, improved oncological outcomes, and enhanced prognostic estimate.[5] Furthermore, it is imperative to identify patients who possess a lower risk for BCR to safeguard them from the adverse consequences associated with additional treatments.[5]

The Cancer of the Prostate Risk Assessment and Kattan nomogram were devised as predictive models for estimating BCR in prostate cancer patients. These models are widely utilized in clinical settings.[6,7] However, classical statistical techniques have their limitations. This work aimed to compare the ML and NN models with the classical statistical model for estimating BCR in patients by utilizing clinical factors, ML, and NN techniques.

MATERIALS AND METHODS

Patients

The prospectively collected data of the patients who underwent RP between November 2011 and May 2022 were retrospectively reviewed. Patients who received preoperative radiotherapy, bacterial infection, distant metastasis or suspicion of distant metastasis, incomplete data, and a follow-up of <1 year were excluded from the study.

All patients underwent robot-assisted RP (RARP) at least 4 weeks after the last transrectal ultrasound (TRUS)-guided prostatic biopsy. Preoperative blood tests were done, and patients were risk-stratified using the National Comprehensive Cancer Network (NCCN) criteria. A multiparametric magnetic resonance imaging (MRI) was performed. The surgery was performed using the Da Vinci Si or Xi system.[7] A bilateral nerve-sparing approach was used where feasible, and bilateral pelvic lymph node dissection was performed.

Data collection

The demographic information and pre- and post-operative parameters were documented. The histological examination of TRUS-guided prostate biopsy tissues was reported using the Gleason grading system. Patients underwent clinical and pathological staging following established protocols. The classification of tumor-node-metastasis was used for the clinical stage. The risk stratification was done according to NCCN guidelines. The term “positive surgical margin” refers to identifying a tumor at the inked boundary during a histopathological examination. Operationally, the BCR was defined as a serum prostate-specific antigen (PSA) level more than 0.2 ng/mL on two separate measurements taken after RP.

Statistical methods

This study’s categorical data were represented using numerical values and percentages. The means and standard deviations were computed for continuous variables. The means of two groups that follow a normal distribution were compared using Student’s t-test. The Mann–Whitney U-test was employed to compare the means of groups that were not normally distributed. We used two statistical tests to analyze the data: Pearson’s Chi-square test and Fisher’s exact test. These tests were utilized to assess the significance of any differences observed in the frequencies of the categorical variables under investigation. The P values below the threshold of 0.05 were considered statistically significant.

The study employed univariable and multivariable regression analyses using Cox proportional hazard regression analysis to determine the BCR. K-nearest neighbor (KNN) and XGboost ML models were generated to predict BCR. KNN finds the sample’s closest neighbors and classifies the samples based on their proximity. XGBoost is an extreme gradient-boosting algorithm. It used iterative ML called gradient boosting. It creates decision trees in a sequential fashion, with each tree fixing the mistakes of the one before it. Then, we used a radial basis function NN (RBFNN) to predict BCR. RBFNN can effectively capture intricate linkages within the data. We split the dataset into training data (70%) and testing data (30%). Accuracy and receiver-operating characteristic (ROC) curve analysis was conducted to evaluate the model’s predictive capability. The statistical analysis was performed using Statistical Product and Service Solutions (SPSS Inc., Chicago, IL, USA version 23.0 for Windows) and RStudio Team (2020). RStudio: Integrated Development for R. RStudio, PBC, Boston, MA, USA.

RESULTS

Patient characteristics

After 916 patients’ data were evaluated and the exclusion criteria were applied, 516 patients were deemed eligible for the study. Of those, 234 (45.3%) developed BCR, and 282 (54.7%) did not. Table 1 provides the demographic, preoperative, intraoperative, and postoperative data. The results showed that the median follow-up period was 24 (15–42) months, and the median BCR diagnosis was made at 12.23 ± 15.58 months.

Table 1.

The demographic data, preoperative, intraoperative, and postoperative data of patients with and without biochemical recurrence

Parameter	Overall (n=516), n (%)	BCR present (n=234; 45.3%), n (%)	BCR absent (n=282; 54.6%), n (%)	P
Age	66 (30–83)	66 (45–83)	64 (30–78)	0.28
Mean BMI	26.6±4.2	26.4±4.6	26.4±7.3	0.31
Hypertension	331 (64.14)	149 (63.7)	182 (64.5)	0.83
Diabetes mellitus	156 (30.23)	79 (33.8)	77 (27.3)	0.11
Other comorbidities	86 (35.09)	38 (16.2)	48 (17)	0.39
Previous history of TURP	23 (4)	10 (4.3)	13 (4.6)	0.85
Charlson comorbidity index	4 (2–10)	5 (2–10)	4 (2–10)
Mean preoperative PSA	21.6±25	29.3±32.1	15.2±14.3	<0.001
Clinical stage
cT1b	11 (2)	5 (2.1)	6 (2.1)	<0.001
cT1c	210 (40.6)	68 (29)	142 (50.4)
cT2a	71 (13.7)	36 (15.3)	35 (12.4)
cT2b	121 (23.4)	69 (29.4)	52 (18.4)
cT2c	88 (17)	51 (21.7)	37 (13.1)
cT3	3 (0.5)	3 (1.3)	0
NCCN risk groups
Very low	8 (1.5)	0	8 (2.8)	<0.001
Low	38 (7.3)	8.(3.4)	30 (10.7)
Favorable intermediate	96 (18.6)	21 (8.9)	75 (26.7)
Unfavorable intermediate	109 (21.12)	34 (14.5)	75 (26.7)
High	238 (46.12)	152 (64.9)	86 (30.6)
Very high	26 (5)	26 (11.1)	7 (2.5)
MRI staging
Organ confined	360 (69.7)	135 (57.5)	225 (80.1)	<0.001
Extraprostatic extension	75 (14.5)	40 (17.1)	35 (12.5)
Seminal vesicle involvement	52 (10)	37 (15.8)	15 (5.3)
LN enlargement >1 cm	20 (3.8)	15 (6.4)	5 (1.8)
TRUS biopsy Gleason grade group	2 (1–5)	3 (1–5)	2 (1–5)	<0.001
Mean maximum core involvement (%)	60.4±35.4	57.2±32.4	54.9±41.2	0.04
Lymphadenectomy
Not done	23 (4.4)	5 (2.1)	18 (6.4)	<0.001
Standard PLND	463 (89.7)	224 (95.7)	239 (84.8)
Extended PLND	30 (5.8)	5 (2.1)	25 (8.9)
Nerve-sparing
None	130 (25.2)	83 (35.5)	47 (16.7)	<0.001
Partial sparing	282 (54.6)	115 (49.1)	167 (59.4)
B/L standard nerve-sparing	101 (19.5)	35 (15)	66 (23.5)
Mean tumor volume in final biopsy (%)	28.85±20.07	37.20±23.08	21.3±13.1	<0.001
Number of positive LN	0 (0–15)	0 (0–15)	0 (0–12)	0.03
Number of LN removed	17 (1–64)	17 (12–23)	17 (1–40)	0.02
ISUP pathological grade
1	68 (13.1)	9 (3.8)	59 (20.9)	<0.001
2	179 (34.6)	53 (22.6)	126 (44.7)
3	111 (21.5)	58 (24.8)	53 (18.8)
4	110 (21.3)	75 (32.1)	35 (12.4)
5	46 (8.9)	39 (16.7)	7 (2.5)
Extracapsular extension in LN	18 (3.4)	15 (6.4)	3 (1)	0.004
Pathological stage
T2a	103 (19.9)	18 (7.7)	88 (31.2)	<0.001
T2b	2 (0.3)	1 (0.4)	1 (0.4)
T2c	91 (17.6)	26 (11.1)	65 (23)
T3a	140 (27.1)	65 (27.8)	75 (26.6)
T3b	177 (34.3)	124 (53)	53 (18.8)
Margins
Negative	347 (67.2)	119 (50.9)	228 (81.1)	<0.001
Single focus on positive margin	96 (18.6)	61 (26.1)	35 (12.5)
Multifocal positive margin	70 (13.5)	54 (23.1)	16 (5.7)
Follow-up (months)	24 (12–132)	36 (12–132)	24 (12–120)
Mean time to BCR (months)		12.23±15.58	NA

Data are presented in median and range or mean±SD wherever applicable. NA=Not applicable, SD=Standard deviation, BMI=Body mass index, BCR=Biochemical recurrence, ISUP=International Society of Urological Pathology, TRUS=Transrectal ultrasound, NCCN=National Comprehensive Cancer Network, PSA=Prostate-specific antigen, LN=Lymph node, PLND=Pelvic LN dissection, MRI=Magnetic resonance imaging, TURP=Transurethral resection of Prostate; B/L=Bilateral

Multivariate analysis

The Cox proportional hazard analysis was utilized for multivariate analysis with the parameters identified as significant in the univariate model. The International Society of Urological Pathology (ISUP) pathological grade, margin status, extracapsular extension, and pathological stage were found to be important model factors by the Cox proportional hazard analysis. Tables 1 and 2 present the findings from the univariate and multivariate analyses, respectively. The area under the curve (AUC) for the multivariate analysis was 0.77 [Table 3 and Figure 1].

Table 2.

Factors found significant on multivariate Cox regression analysis for predicting biochemical recurrence

Parameter	Multivariate analysis
	OR	P
ISUP pathological grade	1.235 (1.081–1.412)	0.002
Extracapsular extension in LN	5.972 (2.194–16.257)	0.004
Margins	1.331 (1.107–1.600)	0.002
Pathological stage	0.827 (0.424–1.613)	0.08

ISUP=International Society of Urological Pathology, LN=Lymph node, OR=Odds ratio

Table 3.

Comparison of all models and the neural network

Model Name	Accuracy	Sensitivity	Specificity	AUC
Cox regression	0.71	0.65	0.78	0.77
K-nearest neighbor	0.66	0.70	0.86	0.69
XGBoost model	0.68	0.62	0.73	0.82
Radial basis NN	0.75	0.72	0.79	0.82

AUC=Area under the curve, XGBoost=Extreme gradient boosting, NN=Neural network

Figure 1.

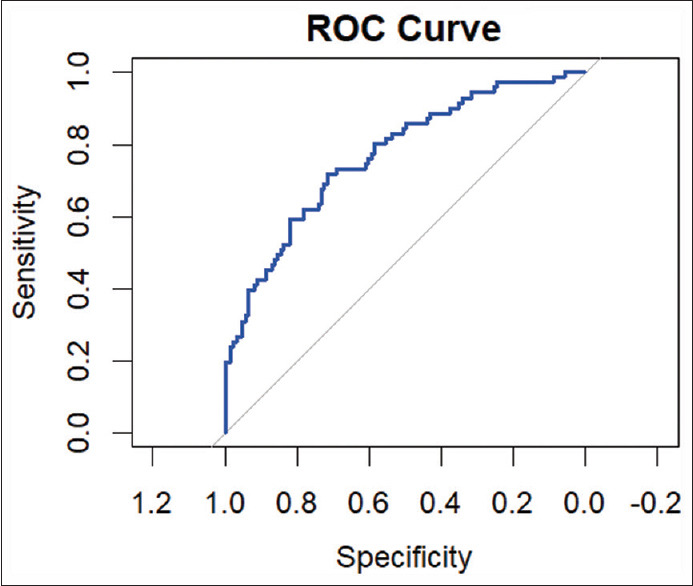
Receiver-operating characteristic of Cox proportional regression model. ROC = Receiver-operating characteristic

Machine learning models

We split the data into training and testing data. Seventy percent of the data were used for training, and 30% of the data were used for testing the model. The factors found significant in the univariate model were used to develop the ML models. The AUCs for ROC curves for KNN [Figure 2] and XGBoost [Figure 3] were 0.69 and 0.82, respectively. The XGBoost model outperformed the conventional statistical regression model in predicting BCR after RP. The increase in AUC from 0.77 to 0.82 is considered significant for model performance. This represents an approximate relative improvement in the model performance by 6.5%. In practical terms, this means that the model’s ability has significantly improved.

Figure 2.

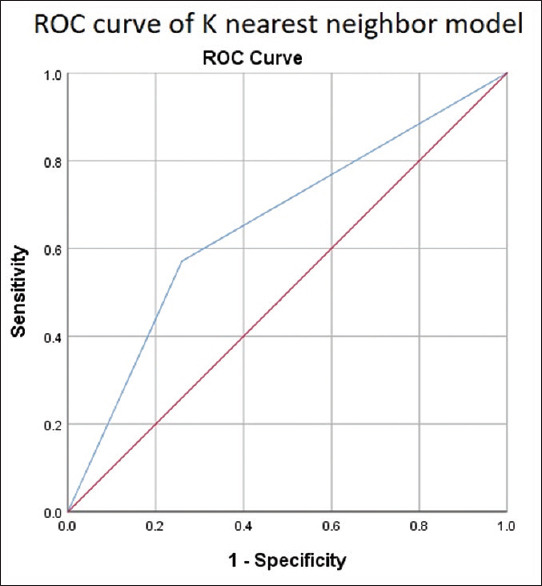
Receiver-operating characteristic curve of K-nearest neighbor. ROC = Receiver -operating characteristic

Figure 3.

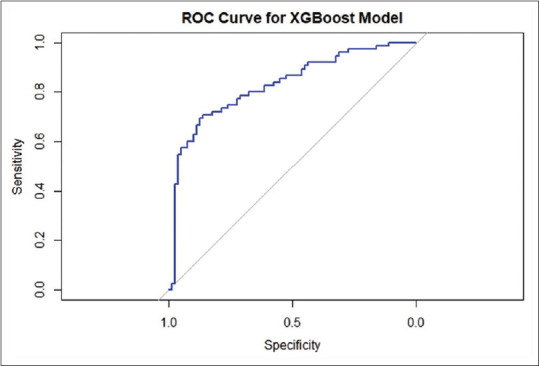
Receiver-operating characteristic curve of XGBoost model. ROC = Receiver-operating characteristic

Radial basis function neural network

The data were split into testing (70%) and training (30%) sets. Using the preoperative serum PSA, MRI staging, ISUP pathological grade, tumor volume in the final biopsy specimen, number of LN removed, number of positive LN, margin positivity, and pathological stage, an input layer of the NN was created [Figure 4]. A hidden layer was generated with the radial basis function, and the output was the prediction of BCR. The AUC of this model was 0.82 [Table 3 and Figure 5].

Figure 4.

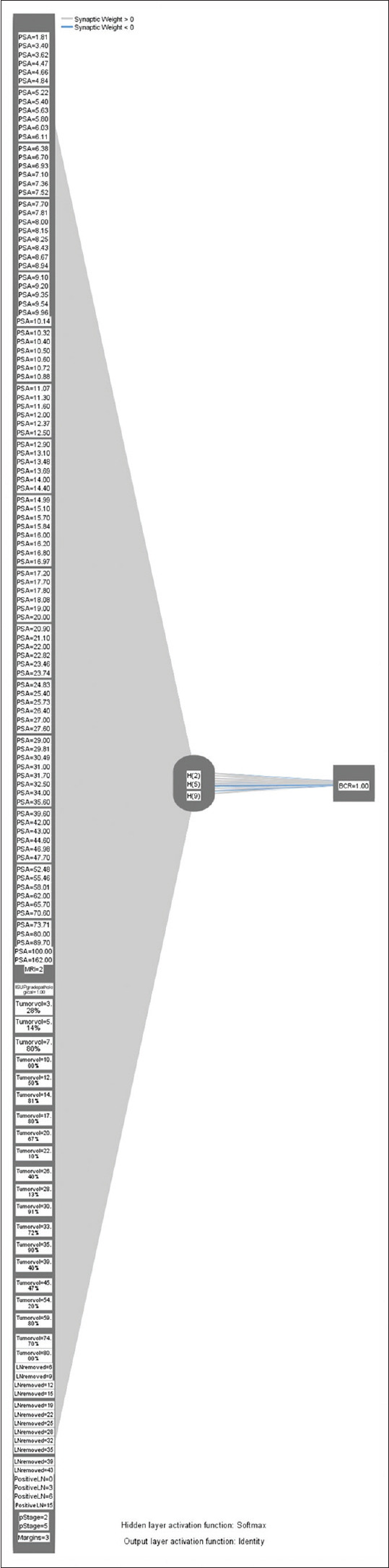
Radial basis function neural network. PSA = Prostate-specific antigen

Figure 5.

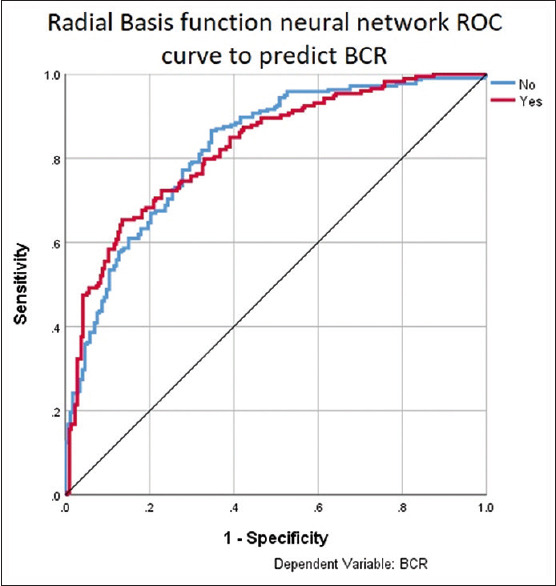
Receiver-operating characteristic curve of radial basis function neural network to predict biochemical recurrence. ROC = Receiver-operating characteristic, BCR = Biochemical recurrence

DISCUSSION

AI is anticipated to significantly impact the field of medicine and healthcare in the near future. It is expected to serve as a valuable tool in screening, diagnosing, and managing a wide range of diseases.[1] “AI” refers to computer technologies that aim to replicate human cognitive functions and engage in problem-solving activities. ML and NN are a field of AI. The utilization of advanced techniques in data analysis allows for the exploration and understanding of complex relationships within datasets. This surpasses the traditional methods of constructing predictive models from a given dataset.[8] ML develops algorithms using different combinations of weights and features. It focuses on the learning aspect of AI and can be used to perform different tasks based on the learning method: unsupervised, semi-supervised, supervised, and reinforcement. There are many ML algorithms that can be used.[9]

We used K-nearest neighbor, XGboost ML model to predict BCR. A popular supervised ML technique for disease prediction is KNN. It considers the features and labels of the training set. The KNN technique can usually classify datasets using a training model that is like the testing query by taking into account the k-nearest training data points (neighbors), the ones closest to the query it is testing. The program then determines which classification should be chosen by a majority voting process. This is the simplest and most widely used ML algorithm.[10] XGBoost stands for extreme gradient boosting. It is an advanced form of gradient boosting algorithm. It is also a supervised ML algorithm but highly powerful, scalable, and optimized. It uses multiple decision trees for prediction and every decision tree corrects the mistakes of the previous decision tree. The decision trees are compiled to identify the most important variables and generate the model. It can handle large and complex data much better than other ML algorithms.[11]

K-nearest neighbor had a lower AUC in our study compared to Cox proportional hazard model. This can be due to its poor ability to handle censored data and its degradation in high-dimensional spaces.[12] XG Boost often outperforms both K-nearest neighbor and the Cox model due to its ability to handle complex relations between data, managing high dimensional data and incorporating regularization to prevent overfitting of the data.[13]

We used RBFNN to predict BCR in our study. A NN takes its inspiration from biological NNs or nervous systems. NN are made of nodes, like cell bodies and connections which are such as axons and dendrites. In an Artificial NN, connections are made between the input variables and nodes. The NN assigns weight to the connections between different nodes according to their capacity to produce the desired result. It is like a nervous system in which the synapses are strengthened when the neurons have correlation output. Similar to the Hebbian theory in neuropsychology: “nerves which fire together, wire together.”[9] RBFNN is different from other NN due to their universal approximation and faster learning. It is composed of three different layers – an input layer, a hidden layer, and an output layer. It uses a linear collection of radially symmetric functions to achieve an input–output mapping.[14]

According to available data, the average duration between RP and the occurrence of BCR and distant metastasis was found to be approximately 8 years. Similarly, the average period between the development of metastatic disease and mortality was observed to be around 5 years. The prediction of BCR, a highly significant marker for assessing the progression to mortality in patients with PCa, has consistently been a primary objective for clinicians engaged in PCa research.[15]

AI has various uses in patients with PCa. Hung et al. used ML and deep learning methods to create a DeepSurv model to predict continence after RARP. They showed that surgeons with more efficient automated performance metrics achieved better continence rates.[16] Wong et al. used three different ML models to predict early BCR post-RP. The ML models could predict BCR with higher accuracy than classical statistical techniques.[17]

This study used localized carcinoma prostate patients from all risk groups. We found that the XGBoost model could predict BCR better than classical statistical analysis. An RBFNN was created to predict BCR, which showed better AUC than the classical statistical and ML models. This model can help prognosticate patients, especially the Indian patient population, for BCR prediction.

The primary strengths of our study are the utilization of comprehensive patient data and follow-up time for the accurate diagnosis or exclusion of BCR. However, a significant drawback of our study is its retrospective nature. Furthermore, it is essential to consider that doing research with larger cohorts of PCa patients and more extended follow-up periods would yield dependable data regarding the applicability of our approach in clinical contexts. The development of these new technologies and the integration of them into health-care information management systems will lead to the acquisition of more accurate algorithms for the diagnosis, treatment, and prognosis of diseases. By integrating these methodologies into a unified national and maybe global network in the future, clinicians will have immediate access to reliable estimations.

CONCLUSION

This study demonstrated that RBFNN and XGBoost models outperform traditional statistical models in predicting BCR. Creating more efficient models would assist medical professionals and patients. It is anticipated that the use of ML and NN methods in health-care settings will experience a rise in the future.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.